Introduction

In inventory system of perishable products, the deterioration is well-known phenomenon that reduces the amount or value of those products with time during storage period. Hence, many business sectors have taken measures, for example, process improvement and advancing storage technology, to control and dilute the deterioration effects. By an effective capital investment in reducing deterioration rate, organizations can reduce non-essential inventory waste and thereby reduces the economic losses and improves business competitiveness. Accordingly, Hsu et al. (2010) first investigated the impact of deteriorating inventory with a constant deterioration rate, time-dependent partial backorders and preservation technology investment. The main objective in their article is to find the retailer’s optimal replenishment and preservation technology investment strategies which maximize the retailer’s profit per unit time and concluded that if the deterioration rate is higher, more investment is needed. Dye and Hsieh (2012) formulated an inventory model with a time-varying deterioration rate and partial backlogging with considering the amount invested in preservation technology. Dye (2013) presented an extended model of Hsu et al. (2010) to considering an inventory system with non-instantaneous deteriorating item and analysis the effect of preservation technology investment. He and Huang (2013) considered a retailer’s lot-sizing problem for deteriorating items and optimal preservation technology investment with price-sensitive demand. Gupta et al. (2013), Singh and Sharma (2013) and Dye and Hsieh (2013) adopted preservation technology investment to the model finite time horizon inventory problem of decaying items which are subject to the supplier’s trade credit. Tsao (2014) extended the model of Dye (2013) to consider a joint location and preservation technology investment decision-making problem for non-instantaneous deterioration items under delay in payments. Yang et al. (2015) formulated a model to determine the optimal trade credit, preservation technology investment and replenishment strategies that maximize the total profit after the default risk occurs over a finite planning horizon due to credit period. Mishra (2016) presented a production inventory model for three-level production rate with characterising the preservation technology for deterioration items under shortages. Zhang et al. (2016) investigated a joint pricing, service, and preservation technology investment policy under common resource constraints. Other researchers such as Dhandapani and Uthayakumar (2016), Dye and Yang (2016), Tayal et al. (2016), Tsao (2016), Shah et al. (2017), Mishra et al. (2017), Saha et al. (2017) and Giri et al. (2017) considered investment in preservation technology.

Promotion is a communication tactic and primary element which educates consumers, increases demand, differentiates brand, and makes the product visible. Normally, organizations use promotion to attract customers through price discount offers, coupons, and free gifts. However, in today’s internet era, organizations promote the product by means of online banner advertisements, social networking websites, blogs, etc., to change the demand pattern of the product. In this context, Cárdenas-Barrón and Sana (2014) investigate the issue of channel coordination for echelon supply chain when demand is sensitive to promotional efforts. Dash et al. (2014) presented the inventory model allowing promotional activities and delay in payment for deteriorating items under inflation with shortages. Cárdenas-Barrón and Sana (2015) presented an economic order quantity inventory model in two-layer supply chain of multi items, where demand is sensitive with promotional effort. Roy et al. (2015) considered a joint venturing of single supplier and single retailer for two-echelon supply chain under variable price and promotional effort. Taleizadeh et al. (2017a, b, c) explored a dual-channel closed-loop supply chain (CLSC) system to investigate the impact of marketing effort on optimal decisions in the CLSC. In this direction, Giri et al. (2015), Palanivel and Uthayakumar (2017), Rajan and Uthayakumar (2017) and Chen et al. (2017) established the models of promotional effort.

In addition, there is widespread study about promotion and pricing. According to marketing team, promotion and price helps to increase the product demand. In this direction, Zhang et al. (2008) presented an analytical model for obtaining optimal decisions on pricing, promotion, and inventory control. Specifically, they studied a single item, finite horizon, periodic review model in which the demand is influenced by price and promotion to maximize the total profit. Tsao and Sheen (2008) investigated the problem of dynamic pricing, promotion, and replenishment policy for a deteriorating item with retailer’s promotional efforts. Wu (2013) presented the bargaining equilibrium behaviour of an industry in supply chain with price and promotional effort-dependent demand. Maihami and Karimi (2014) presented the problem of pricing and replenishment policy for non-instantaneous deteriorating items subject to promotional efforts.

There has been substantial and growing literature that describes price–demand relationship linking the inventory policy and price together through demand (see, Taleizadeh et al. 2015a, b, 2016, 2017a, b, c; Taleizadeh and Daryan 2015, 2016; Zerang et al. 2017; Taleizadeh and Baghban 2017; Daryan et al. 2017). The model in this article shows the pattern of stochastic price-dependent demand. The uncertainty of demand is decided on the basis of quantity of stock and selling price. Commonly, random demand is defined as \(D\left( {p,\varepsilon } \right) = d\left( p \right) + \varepsilon\) in the additive case and \(D(p,\varepsilon ) = d(p) \cdot \varepsilon\) in the multiplicative case, wherein \(d(p)\) is deterministic decreasing function that captures dependency between demand and price and \(\varepsilon\) is a random variable defined on finite range. The shape of demand curve is deterministic and price related. Numerous researchers, such as Federgruen and Heching (1999), presented a combined pricing and inventory control model under uncertainty. Then, Petruzzi and Dada (1999) presented a pricing and newsvendor problem. Chen and Simchi-Levi (2004) investigated a pricing strategy and inventory control with random demand. Zhang et al. (2008) investigated the optimal decision on price, promotion and inventory control subject to stochastic demand. Pang (2011) presented that optimize the price and inventory control with stock deterioration and partial backordering. Chao et al. (2012) presented a model on pricing policy in capacitated stochastic inventory system. Zhu (2012) presented a decision on pricing and replenishment with returns and expenditure. Zhu and Cetinkaya (2015) consider an immediate inventory liquidation decision on liquidation quantity, where demand during the liquidation period (DDLP) is a random variable, whose distribution depends on the promotional price. Recently, Roy et al. (2016), Jauhari et al. (2016), Wangsa and Wee (2017), and AlDurgam et al. (2017) presented an inventory model under stochastic demand.

Based on the above discussion, this study aims at formulating profit maximization inventory model for deteriorating items with stochastic price sensitive demand and promotional efforts. The generalized time proportional deterioration and partial backlogging rates are used in model formulation. An inventory system, wherein shortages followed by inventory is considered. Furthermore, it is assumed that the deterioration rate is controlled by preservation technology investment. An analytical approach for inventory decisions is developed under various partial backlogging issues. In addition, it is shown that the total profit per time unit is concave function of price and preservation technology cost when other decision variables are fixed. Finally, numerical examples are provided to illustrate the theoretical results and a sensitivity analysis of the optimal solution with respect to major parameters is also carried out.

The rest of the paper is organized as follows. The next section describes the notation and assumptions used throughout this paper. The subsequent section analyzes the inventory model starting shortages. Some numerical examples to illustrate the solution procedure are provided, and sensitivity analysis of the major parameters is also carried out in section before the conclusion, and the conclusions and suggestion for future research are given in final section.

Notation and assumptions

The mathematical model in this paper is developed on the basis of the following notation and assumptions.

Notation

Decision variable

\(t_{1}\) :

The replenishment point, the duration of shortage period is \(\left[ {0,t_{1} } \right]\)

\(t_{2}\) :

The length of time after which inventory reaches to zero

\(p\) :

The selling price per unit

\(\xi\) :

The preservation technology cost per unit

Parameters

\(A\) :

The ordering cost per order

\(C\) :

The purchasing cost per unit

\(C_{\text{h}}\) :

The holding cost per unit per time unit

\(C_{\text{b}}\) :

The backorder cost per unit per time unit

\(C_{\text{l}}\) :

The lost sale cost per unit

\(\varepsilon\) :

The random variable of the demand function with \(E(\varepsilon ) = \mu\)

\(\rho\) :

The promotional effort, \(\rho \ge 1\)

\(w\) :

Maximum capital investment in preservation technology

Variables

\(Q\) :

The ordering quantity per cycle

\(I_{\text{n}} (t)\) :

The level of negative inventory at time \(t\), where \(0 \le t \le t_{1}\)

\(I_{\text{p}} \left( t \right)\) :

The level of positive inventory at time \(t\), where \(t_{1} \le t \le t_{1} + t_{2}\)

\(m(\xi )\) :

Proportion of reduced deterioration rate, \(0 \le m\left( \xi \right) \le 1\)

\(\varPi_{A}\) :

The total profit per unit time of inventory system

Assumptions

(These assumptions are mainly adopted from Maihami and Karimi 2014; Sana 2010):

  1. 1.

    Replenishment rate is infinite, but its order size is finite.

  2. 2.

    The basic demand function is \(D(p) + \varepsilon\), where \(D(p)\) a decreasing and deterministic function of selling price is \(p\) and \(\varepsilon\) is a non-negative and continuous random variable with \(E(\varepsilon ) = \mu\).

  3. 3.

    The promotional effort cost \({\text{PC}}\) is an increasing function of the promotional effort and the basic demand \({\text{PC}} = K\left( {\rho - 1} \right)^{2} \left[ {\int_{0}^{1} { (D(p) + \varepsilon ) {\text{d}}t} } \right]^{\alpha }\), where \(K > 0\) and \(\alpha\) is a constant. Both the market demand and the cost of the promotional effort will increase as the promotional effort increases.

  4. 4.

    The demand function is influenced by promotional effort \(\rho\) and can be expressed by mark-up over the promotional effort, i.e., \(\rho (D(p) + \varepsilon )\).

  5. 5.

    The item deteriorates at a time-varying rate of deterioration \(\theta (t)\), where \(0 < \theta (t) < 1.\) Besides, there is no repair or replacement of deteriorated units during the replenishment cycle.

  6. 6.

    The proportion of reduced deterioration rate, \(m(\xi )\) is a continuous, concave, and increasing function of capital investment.

  7. 7.

    Shortages are allowed. The inventory model starts with shortage and ends with zero inventory. Some fraction of demand during stock-out situation is backordered, and rest of the demand is partially backlogged.

Model formulation

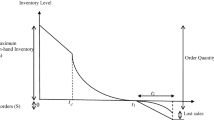
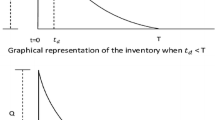
This study considers the inventory model that starts with shortages. Shortages begin to be accumulated during \(\left[ {0,t_{1} } \right]\) which are partially backlogged. The backlogged demand is satisfied at the replenishment point \(t_{1}\) and rest of lot size adjusts the demand up to time \(t_{2}\). From Fig. 1, it can be seen that the depletion of the inventory occurs due to the combined effects of demand and deterioration during the time interval \(\left[ {t_{1} ,t_{2} } \right]\). Deterioration is reduced by preservation technology. This process is repeated as mentioned above.

Fig. 1
figure 1

Graphical representation of inventory system

Full size image

Based on above description, the status of negative inventory at any instant of time \(t \in \left[ {0,t_{1} } \right]\) is governed by differential equation:

$$\frac{{{\text{d}}I_{\text{n}} (t)}}{{{\text{d}}t}} = - \rho (D(p) + \varepsilon )\beta (t_{1} - t),\quad 0 \le t \le t_{1}$$
(1)

with \(I_{\text{n}} (0) = 0\).

Solving differential equation given in (1) yields

$$I_{\text{n}} (t) = - \rho (D(p) + \varepsilon )\int_{0}^{t} {\beta (t_{1} - t){\text{d}}t}$$
(2)

and the status of positive inventory at any instant of time \(t \in \left[ {0,t_{2} } \right]\) is governed by differential equation:

$$\frac{{{\text{d}}I_{\text{p}} (t)}}{{{\text{d}}t}} = - \theta (t)(1 - m(\xi ))I_{\text{p}} (t) - \rho (D(p) + \varepsilon ),\quad 0 \le t \le t_{2}$$
(3)

with \(I_{\text{p}} (t_{2} ) = 0.\).

Solving differential equation defined in (3), one has

$$I_{\text{p}} (t) = \rho (D(p) + \varepsilon ){\text{e}}^{ - ((1 - m(\xi ))g(t))} \int_{0}^{{t_{2} }} {{\text{e}}^{(1 - m(\xi ))g(x)} {\text{d}}x} ,$$
(4)

where \(g(t) = \int_{0}^{t} {\theta (x){\text{d}}x} .\).

Therefore, the lost sale quantity at time t is

$$I_{\text{l}} (t) = \rho (D(p) + \varepsilon )[1 - \beta (t_{1} - t)],\quad 0 \le t \le t_{1} .$$
(5)

The replenishment size (including back logged) is

$$Q = \{ I_{\text{p}} (0) - I_{\text{n}} (t_{1} )\} = \rho \left( {D(p) + \varepsilon } \right)\left\{ {{\text{e}}^{ - (1 - m(\xi ))g(0)} \int_{0}^{{t_{2} }} {{\text{e}}^{(1 - m(\xi ))g(x)} {\text{d}}x + \int_{0}^{{t_{1} }} {\beta (t_{1} - t){\text{d}}t} } } \right\}.$$
(6)

Total cost of lost sale during time span \([0,t_{1} ]\) is

$${\text{TLC}} = E\left( {C_{\text{l}} \int_{0}^{{t_{1} }} {I_{\text{l}} (t){\text{d}}t} } \right) = C_{l} \rho \left( {D(p) + \mu } \right)\int_{0}^{{t_{1} }} {\left[ {1 - \beta (t_{1} - t)} \right]{\text{d}}t} .$$

Total cost of back logged for stock-out during time span \([0,t_{1} ]\) is

$${\text{TSC}} = E\left( {C_{\text{b}} \int_{0}^{{t_{1} }} {\left[ { - I_{\text{n}} (t)} \right]{\text{d}}t} } \right) = C_{\text{b}} \rho \left( {D\left( p \right) + \mu } \right)\int_{0}^{{t_{1} }} {\left[ {\int_{0}^{t} {\beta \left( {t_{1} - x} \right){\text{d}}x} } \right]{\text{d}}t} .$$

Total holding cost during time span \([0,t_{2} ]\) is

$${\text{TIC}} = E\left( {C_{\text{h}} \int_{0}^{{t_{2} }} {I_{\text{p}} (t){\text{d}}t} } \right) = C_{\text{h}} \rho \left( {D(p) + \mu } \right)\int_{0}^{{t_{2} }} {{\text{e}}^{ - (1 - m(\xi ))g(t)} \left[ {\int_{t}^{{t_{2} }} {{\text{e}}^{(1 - m(\xi ))g(x)} {\text{d}}x} } \right]{\text{d}}t} .$$

Total purchasing cost is

$${\text{TPC}} = E\left( {C \cdot Q} \right) = C\rho \left( {D\left( p \right) + \mu } \right)\left\{ {{\text{e}}^{{ - \left( {1 - m\left( \xi \right)} \right)g\left( 0 \right)}} \int_{0}^{{t_{2} }} {{\text{e}}^{{\left( {1 - m\left( \xi \right)} \right)g\left( x \right)}} {\text{d}}x + \int_{0}^{{t_{1} }} {\beta (t_{1} - t){\text{d}}t} } } \right\}.$$

Total sales revenue is

$${\text{TRV}} = E\left( {p\left\{ {\rho \left( {D\left( p \right) + \varepsilon } \right)\int_{0}^{{t_{2} }} {{\text{d}}t} + \left( { - I_{\text{n}} \left( {t_{1} } \right)} \right)} \right\}} \right) = p\rho \left( {D\left( p \right) + \mu } \right)\left\{ {t_{2} + \int_{0}^{{t_{1} }} {\beta (t_{1} - t){\text{d}}t} } \right\}.$$

The preservation technology cost is

$${\text{PTC}} = \left( {t_{1} + t_{2} } \right)\xi .$$

The promotional cost is

$${\text{PC}} = E\left( {K(\rho - 1)^{2} \left[ {\int_{0}^{{t_{1} + t_{2} }} { (D(p) + \varepsilon ) {\text{d}}t} } \right]^{\alpha } } \right) = K\left[ {(t_{1} + t_{2} )(D(p) + \mu )} \right]^{\alpha } ( - 1 + \rho )^{2} .$$

Assembling all the cost and profit factors, the total profit (denoted by \(\varPi (t_{1} ,t_{2} ,p,\xi )\)) is given by

$$\begin{aligned} \varPi (t_{1} ,t_{2} ,p,\xi ) & = {\text{TRV}} - (A + {\text{TSC}} + {\text{TLC}} + {\text{TIC}} + {\text{TPC}} + {\text{PTC}} + {\text{PC}}) \\ & = p \cdot \rho \left( {D(p) + \mu } \right)\left\{ {t_{2} + \int_{0}^{{t_{1} }} {\beta \left( {t_{1} - t} \right){\text{d}}t} } \right\} - A \\ & \quad - \rho \cdot C_{b} \left( {D(p) + \mu } \right)\int_{0}^{{t_{1} }} {\left\{ {\int_{0}^{t} {\beta \left( {t_{1} - x} \right){\text{d}}x} } \right\}{\text{d}}t} \\ & \quad - C_{l} \cdot \rho \left( {D\left( p \right) + \mu } \right)\int_{0}^{t} {\left\{ {1 - \beta (t_{1} - t)} \right\}} {\text{d}}t \\ & \quad - C_{h} \cdot \rho \left( {D(p) + \mu } \right)\int_{0}^{{t_{2} }} {{\text{e}}^{ - (1 - m(\xi ))g(t)} } \left\{ {\int_{t}^{{t_{2} }} {{\text{e}}^{(1 - m(\xi ))g(x)} {\text{d}}x} } \right\} \\ & \quad - C \cdot \rho \left( {D(p) + \mu } \right)\left\{ {{\text{e}}^{{ - \left( {1 - m\left( \xi \right)} \right)g\left( 0 \right)}} \int_{0}^{{t_{2} }} {{\text{e}}^{{\left( {1 - m(\xi )} \right)g(x)}} {\text{d}}x} + \int_{0}^{{t_{1} }} {\beta (t_{1} - t){\text{d}}t} } \right\} \\ & \quad - (t_{1} + t_{2} )\xi - K\{ (t_{1} + t_{2} )(D(p) + \mu )\}^{\alpha } ( - 1 + \rho )^{2} . \\ \end{aligned}$$
(7)

Therefore, the total profit per unit time is

$$\varPi_{A} \left( {t_{1} ,t_{2} ,\xi ,p} \right) = \frac{{\varPi \left( {t_{1} ,t_{2} ,\xi ,p} \right)}}{{t_{1} + t_{2} }}.$$
(8)

So that the optimization problem addressed in this paper is

$$\begin{aligned} & \mathop {\hbox{max} }\limits_{{t_{1} ,t_{2} ,p,\xi }} \varPi_{A} \left( {t_{1} ,t_{2} ,p,\xi } \right) \\ & {\text{subject}}\;{\text{to}}\;\;C \le p,\quad 0 \le \xi \le w,\;{\text{and}}\;t_{1} ,t_{2} \ge 0 { } .\\ \end{aligned}$$
(9)

The problem defined in (9) can be solved by decomposing maximum operator in three stages:

First with respect to \(\left( {t_{1} ,t_{2} } \right)\), second with respect to \(p\), and then with respect to \(\xi\), that is

$$\begin{aligned} & \mathop {\hbox{max} }\limits_{\xi } \left\{ {\mathop {\hbox{max} }\limits_{p} \left\{ {\mathop {\hbox{max} }\limits_{{t_{1} ,t_{2} }} \, \varPi_{A} \left( {t_{1} ,t_{2} ,p,\xi } \right)} \right\}} \right\} \\ & {\text{subject}}\;{\text{to}}\;\;C \le p,\quad 0 \le \xi \le w,\;{\text{and}}\;t_{1} ,t_{2} \ge 0.\\ \end{aligned}$$
(10)

Keeping \(\xi ,p\) as fixed, we have the partial derivatives of \(\varPi_{A}\) with respect to \(t_{1}\) and \(t_{2}\) as follows:

$$\frac{{\partial \varPi_{A} \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{1} }} = - \frac{{\varPi \left( {t_{1} ,t_{2} } \right)}}{{\left( {t_{1} + t_{2} } \right)^{2} }} + \frac{1}{{t_{1} + t_{2} }}\left( {\frac{{\partial \varPi \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{1} }}} \right).$$
(11)
$$\frac{{\partial \varPi_{A} \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{2} }} = - \frac{{\varPi \left( {t_{1} ,t_{2} } \right)}}{{\left( {t_{1} + t_{2} } \right)^{2} }} + \frac{1}{{t_{1} + t_{2} }}\left( {\frac{{\partial \varPi \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{2} }}} \right),$$
(12)
$$\frac{{\partial^{2} \varPi_{A} \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{1}^{2} }} = \frac{{2\varPi \left( {t_{1} ,t_{2} } \right)}}{{\left( {t_{1} + t_{2} } \right)^{3} }} - \frac{2}{{\left( {t_{1} + t_{2} } \right)^{2} }}\left( {\frac{{\partial \varPi \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{1} }}} \right) + \frac{1}{{t_{1} + t_{2} }}\left( {\frac{{\partial^{2} \varPi \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{1}^{2} }}} \right),$$
(13)
$$\frac{{\partial^{2} \varPi_{A} \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{2}^{2} }} = \frac{{2\varPi \left( {t_{1} ,t_{2} } \right)}}{{\left( {t_{1} + t_{2} } \right)^{3} }} - \frac{2}{{\left( {t_{1} + t_{2} } \right)^{2} }}\left( {\frac{{\partial \varPi \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{2} }}} \right) + \frac{1}{{t_{1} + t_{2} }}\left( {\frac{{\partial^{2} \varPi \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{2}^{2} }}} \right).$$
(14)

Now, the necessary condition for \(\varPi_{A} (t_{1} ,t_{2} )\) to be optimum is

$$\frac{{\partial \varPi_{A} \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{1} }} = \frac{{\partial \varPi_{A} \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{2} }} = 0.$$
(15)

Hence, it follows from (11) to (14) that

$$\varPi \left( {t_{1} ,t_{2} } \right) = \left( {t_{1} + t_{2} } \right)\left( {\frac{{\partial \varPi \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{1} }}} \right),$$
(16)
$$\varPi \left( {t_{1} ,t_{2} } \right) = \left( {t_{1} + t_{2} } \right)\left( {\frac{{\partial \varPi \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{2} }}} \right),$$
(17)
$$\frac{{\partial^{2} \varPi_{A} \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{1}^{2} }} = \frac{1}{{t_{1} + t_{2} }}\left( {\frac{{\partial^{2} \varPi \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{1}^{2} }}} \right),$$
(18)
$$\frac{{\partial^{2} \varPi_{A} \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{2}^{2} }} = \frac{1}{{t_{1} + t_{2} }}\left( {\frac{{\partial^{2} \varPi \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{2}^{2} }}} \right).$$
(19)

On equating (16) and (17), one has

$$\frac{{\partial \varPi \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{1} }} = \frac{{\partial \varPi \left( {t_{1} ,t_{2} } \right)}}{{\partial t_{2} }}.$$
(20)

Next, the first-order partial derivative of \(\varPi \left( {t_{1} ,t_{2} } \right)\) with respect to \(t_{1}\) and \(t_{2}\), respectively, is

$$\begin{aligned} \frac{\partial \varPi }{{\partial t_{1} }} & = p \cdot \rho \left( {D\left( p \right) + \mu } \right)\left\{ {\int_{0}^{{t_{1} }} {\frac{{\partial \beta \left( {t_{1} - t} \right)}}{{\partial t_{1} }}{\text{d}}t + \beta \left( 0 \right)} } \right\} - C_{b} \cdot \rho \left( {D\left( p \right) + \mu } \right) \\ & \quad \left\{ {\int_{0}^{{t_{1} }} {\left( {\int_{0}^{t} {\frac{{\partial \beta \left( {t_{1} - x} \right)}}{{\partial t_{1} }}{\text{d}}x} } \right){\text{d}}t} + \int_{0}^{{t_{1} }} {\beta \left( {t_{1} - t} \right){\text{d}}t} } \right\} - C_{l} \cdot \rho \left( {D\left( p \right) + \mu } \right) \\ & \quad - \left\{ {\int_{0}^{{t_{1} }} {\frac{{\partial \beta \left( {t_{1} - t} \right)}}{{\partial t_{1} }}} - \beta \left( 0 \right) + 1} \right\} - C \cdot \rho (D(p) + \mu )\left\{ {\int_{0}^{{t_{1} }} {\frac{{\partial \beta \left( {t_{1} - t} \right)}}{{\partial t_{1} }}} + \beta \left( 0 \right)} \right\} \\ & \quad - \frac{{K\left[ {\left( {t_{1} + t_{2} } \right)\left( {D\left( p \right) + \mu } \right)} \right]^{\alpha } \alpha \left( {\rho - 1} \right)^{2} }}{{\left( {t_{1} + t_{2} } \right)}} - \xi . \\ \end{aligned}$$
(21)
$$\begin{aligned} \frac{\partial \varPi }{{\partial t_{2} }} & = p \cdot \rho \left( {D\left( p \right) + \mu } \right) - C\rho \left( {D\left( p \right) + \mu } \right)\left\{ {{\text{e}}^{{\left( {1 - m\left( \xi \right)} \right)\left( {g\left( {t_{2} } \right) - g\left( 0 \right)} \right)}} } \right\} - C_{\text{h}} \rho \left( {D\left( p \right) + \mu } \right) \\ & \left\{ {\int_{0}^{{t_{2} }} {{\text{e}}^{{\left( {1 - m\left( \xi \right)} \right)\left( {g\left( {t_{2} } \right) - g\left( t \right)} \right)}} dt} } \right\} - \frac{{K\left[ {\left( {t_{1} + t_{2} } \right)\left( {D(p) + \mu } \right)} \right]^{\alpha } \alpha \left( {\rho - 1} \right)^{2} }}{{\left( {t_{1} + t_{2} } \right)}} - \xi . \\ \end{aligned}$$
(22)

On substituting the expressions for \(\frac{\partial \varPi }{{\partial t_{1} }}\) and \(\frac{\partial \varPi }{{\partial t_{2} }}\) into (20), one has

$$\begin{aligned} \therefore \; & p - p\left\{ {\int_{0}^{{t_{1} }} {\frac{{\partial \beta \left( {t_{1} - t} \right)}}{{\partial t_{1} }}{\text{d}}t + \beta \left( 0 \right)} } \right\} + C_{\text{b}} \left\{ {\int_{0}^{{t_{1} }} {\left( {\int_{0}^{t} {\frac{{\partial \beta \left( {t_{1} - x} \right)}}{{\partial t_{1} }}{\text{d}}x} } \right){\text{d}}t} + \int_{0}^{{t_{1} }} {\beta \left( {t_{1} - x} \right){\text{d}}x} } \right\} \\ & - C_{l} \left\{ {\int_{0}^{{t_{1} }} {\frac{{\partial \beta \left( {t_{1} - t} \right)}}{{\partial t_{1} }}} + \beta \left( 0 \right) - 1} \right\} + C\left\{ {\int_{0}^{{t_{1} }} {\frac{{\partial \beta \left( {t_{1} - t} \right)}}{{\partial t_{1} }} + \beta \left( 0 \right)} } \right\} \\ & = C\left\{ {{\text{e}}^{{\left( {1 - m\left( \xi \right)} \right)\left( {g\left( {t_{2} } \right)} \right)}} } \right\} + C_{\text{h}} \left\{ {\int_{0}^{{t_{2} }} {{\text{e}}^{{\left( {1 - m\left( \xi \right)} \right)\left( {g\left( {t_{2} } \right) - g\left( t \right)} \right)}} {\text{d}}t} } \right\}. \\ \end{aligned}$$
(23)

According to the previous literatures, \(\beta \left( x \right)\) is considered as either rational or exponential function, i.e., \(\beta \left( x \right) = \frac{1}{1 + \delta x}\) (cf. Papachristos and Skouri 2003; Maihami and Karimi 2014) or \(\beta \left( x \right) = \exp \left[ { - \delta x} \right]\)(cf. Papachristos and Skouri 2000; Dye et al. 2007; Sana 2010).

Case 1

Let \(\beta \left( x \right) = \frac{1}{1 + \delta \left( x \right)}\), \(g\left( t \right) = \int_{0}^{t} {\theta \left( t \right){\text{d}}t} ,\;\;g\left( 0 \right) = 0\), \(\int_{0}^{{t_{1} }} {\frac{\partial \beta }{{\partial t_{1} }}{\text{d}}t} = - \frac{{\delta t_{1} }}{{1 + \delta t_{1} }}\), \(\int_{0}^{{t_{1} }} {\frac{\partial \beta }{{\partial t_{1} }}{\text{d}}t} + \beta \left( 0 \right) = \frac{1}{{1 + \delta t_{1} }}\), \(\int_{0}^{{t_{1} }} {\left( {\int_{0}^{t} {\frac{{\partial \beta \left( {t_{1} - x} \right)}}{{\partial t_{1} }}{\text{d}}x} } \right)} {\text{d}}t + \int_{0}^{{t_{1} }} {\beta \left( {t_{1} - t} \right){\text{d}}t} = \frac{{t_{1} }}{{1 + \delta t_{1} }}\), \(\frac{\partial \beta }{{\partial t_{1} }} = - \frac{\delta }{{\left\{ {1 + \delta \left( {t_{1} - t} \right)} \right\}^{2} }},\;\;\frac{{\partial^{2} \beta }}{{\partial t_{1}^{2} }} = \frac{{2\delta^{2} }}{{\left\{ {1 + \delta \left( {t_{1} - t} \right)} \right\}^{3} }}\), \(\int_{0}^{t} {\frac{{\partial^{2} \beta }}{{\partial t_{1}^{2} }}{\text{d}}t} + \frac{\partial \beta \left( 0 \right)}{{\partial t_{1} }} = - \frac{\delta }{{1 + \delta t_{1} }},\int_{0}^{{t_{1} }} {\frac{\partial \beta }{{\partial t_{1} }}{\text{d}}t} + \beta \left( 0 \right) = \frac{1}{{1 + \delta t_{1} }},\int_{0}^{{t_{1} }} {\left( {\int_{0}^{t} {\frac{{\partial^{2} \beta \left( {t_{1} - x} \right)}}{{\partial t_{1}^{2} }}{\text{d}}x} } \right){\text{d}}t = 0} .\)

Substitute these in (23), we get

$$\frac{{\left( {C_{b} + \delta \left( {p + C_{l} - C} \right)} \right)t_{1} }}{{1 + \delta t_{1} }} = C\left( {{\text{e}}^{{\left( {1 - m\left( \xi \right)} \right)g\left( {t_{2} } \right)}} } \right) + C_{h} \int_{0}^{{t_{2} }} {{\text{e}}^{{\left( {1 - m\left( \xi \right)} \right)\left( {g\left( {t_{2} } \right) - g\left( t \right)} \right)}} {\text{d}}t} .$$
(24)

For notational convenience, we take

$$\begin{aligned} \Delta \left( p \right) & = \frac{A}{{\rho \left( {D\left( p \right) + \mu } \right)}} + \frac{2C}{\delta } - \left( {\frac{V(p)}{{\delta^{2} }} + \frac{{C^{2} }}{V\left( p \right)}} \right) + \frac{V(p)}{{\delta^{2} }}\left( {\ln \left( {\frac{V\left( p \right)}{V(p) - 2C}} \right)} \right) \\ & \quad - \frac{{K\left( {\alpha - 1} \right)\left( {\rho - 1} \right)^{2} \left[ {C\left( {D\left( p \right) + \mu } \right)} \right]^{\alpha } }}{{\rho \left( {D\left( p \right) + \mu } \right)\left[ {V\left( p \right) - \delta C} \right]^{\alpha } }}. \\ \end{aligned}$$
(25)

Lemma 1

For known p and \(\xi\), we have

  1. (a)

    If \(\Delta \left( p \right) > 0\) then there exist unique pair of values \(\left( {t_{1} ,t_{2} } \right) = \left( {t_{1}^{\prime } ,t_{2}^{\prime } } \right)\) which satisfies (15).

  2. (b)

    If \(\Delta \left( p \right) \le 0\) then the optimal value occurs at point \(\left( {t_{1} ,t_{2} } \right) = \left( {\frac{C}{{\left[ {V\left( p \right) - \delta C} \right]}},0} \right).\)

Proof

Refer to Appendix A.

Suppose \(\left( {t_{1}^{*} ,t_{2}^{*} } \right)\) denotes the optimal value of \(\left( {t_{1} ,t_{2} } \right)\), then we can obtain following result.

Theorem 1

For fixed \(p\) and \(\xi\), total profit function \(\varPi_{A} \left( {t_{1} ,t_{2} ,p,\xi } \right)\) is concave and reaches its global maximum at point \(\left( {t_{1} ,t_{2} } \right) = \left( {t_{1}^{*} ,t_{2}^{*} } \right)\).

Proof

Refer to Appendix B.

Hence, the value of \(\left( {t_{1}^{*} ,t_{2}^{*} } \right)\) gives global maximum for the problem in (9).

Case 2

Let \(\beta \left( x \right) = \exp \left[ { - \delta \left( x \right)} \right]\) and \(g(t) = \int_{0}^{t} {\theta (t){\text{d}}t}\), \(g\left( 0 \right) = 0,\)\(\int_{0}^{{t_{1} }} {\beta \left( {t_{1} - t} \right)dt} = {{\left( {1 - \exp \left( { - \delta t_{1} } \right)} \right)} \mathord{\left/ {\vphantom {{\left( {1 - \exp \left( { - \delta t_{1} } \right)} \right)} \delta }} \right. \kern-0pt} \delta }\), \(\int_{0}^{t} {\frac{\partial \beta }{{\partial t_{1} }} + \beta \left( 0 \right) = \exp \left[ { - \delta t_{1} } \right]}\), \(\int_{0}^{{t_{1} }} {\left( {\int_{0}^{t} {\frac{{\partial \beta \left( {t_{1} - x} \right)}}{{\partial t_{1} }}{\text{d}}x} } \right){\text{d}}t} = {{\left\{ {\left( {1 + \delta t_{1} } \right)\exp \left[ { - \delta t_{1} } \right] - 1} \right\}} \mathord{\left/ {\vphantom {{\left\{ {\left( {1 + \delta t_{1} } \right)\exp \left[ { - \delta t_{1} } \right] - 1} \right\}} {\delta .}}} \right. \kern-0pt} {\delta .}}\)

Substituting these in (23), we get

$$\left( {p - C + C_{l} } \right)\left( {1 - e^{{\left( { - \delta t_{1} } \right)}} } \right) + C_{\text{b}} t_{1} e^{{^{{\left( { - \delta t_{1} } \right)}} }} = C\left( {{\text{e}}^{{\left( {1 - m\left( \xi \right)} \right)\left( {g\left( {t_{2} } \right)} \right)}} } \right) + C_{\text{h}} \left( {\int\limits_{0}^{{t_{2} }} {{\text{e}}^{{\left( {1 - m\left( \xi \right)} \right)\left( {g\left( {t_{2} } \right) - g\left( t \right)} \right)}} {\text{d}}t} } \right).$$
(26)

Proceeding as in Case 1, it can be shown that \(\varPi_{A} \left( {t_{1} ,t_{2} ,p,\xi } \right)\) is concave and reaches its global maximum at point \(\left( {t_{1} ,t_{2} } \right) = \left( {t_{1}^{*} ,t_{2}^{*} } \right)\).

Hence, the value of \(\left( {t_{1}^{*} ,t_{2}^{*} } \right)\) gives global maximum for the optimizing problem (9).

Next, we examine the condition for which the optimal selling price \(p\) exists. Keeping \(\xi\), \(t_{1}^{*}\) and \(t_{2}^{*}\) as fixed, taking the first-order derivative of \(\varPi_{\rm A} \left( {t_{1}^{*} ,t_{2}^{*} ,p,\xi } \right)\) with respect to \(p\), we obtain

$$\begin{aligned} \frac{{\partial \varPi_{A} }}{\partial p} & = - \left[ {\frac{{\rho D^{\prime}\left( p \right)}}{{t_{1}^{*} + t_{2}^{*} }}\left\{ {\left( { - p + C_{l} + C} \right)\left( {\int\limits_{0}^{{t_{1}^{*} }} {\beta \left( {t_{1}^{*} - t} \right){\text{d}}t} } \right) + C_{\text{b}} \left( {\int\limits_{0}^{{t_{1}^{*} }} {\left( {\int\limits_{0}^{t} {\beta \left( {t_{1}^{*} - x} \right){\text{d}}x} } \right){\text{d}}t} } \right)} \right.} \right. \\ & \quad + C_{\text{h}} \left( {\int\limits_{0}^{{t_{2}^{*} }} {\int\limits_{t}^{{t_{2}^{*} }} {{\text{e}}^{{\left( {1 - m\left( \xi \right)} \right)\left[ {g\left( x \right) - g\left( t \right)} \right]}} {\text{d}}x{\text{d}}t} } } \right)\left. { - pt_{2}^{*} - C_{\text{l}} t_{1}^{*} + C\left( {\int\limits_{0}^{{t_{2}^{*} }} {{\text{e}}^{{\left( {1 - m\left( \xi \right)} \right)g\left( x \right)}} {\text{d}}x} } \right)} \right\} \\ & \quad - \frac{{\rho \left( {D\left( p \right) + \varepsilon } \right)}}{{t_{1}^{*} + t_{2}^{*} }}\left\{ {t_{2}^{*} + \int\limits_{0}^{{t_{1}^{*} }} {\beta \left( {t_{1}^{*} - t} \right){\text{d}}t} } \right\}\left. { + K\left[ {\left( {t_{1}^{*} + t_{2}^{*} } \right)\left( {D\left( p \right) + \varepsilon } \right)} \right]^{\alpha - 1} \alpha D^{\prime}\left( p \right)\left( {\rho - 1} \right)^{2} } \right]. \\ \end{aligned}$$
(27)

Then, the second partial derivative of the profit function \(\varPi_{\rm A} \left( {t_{1}^{*} ,t_{2}^{*} ,p,\xi } \right)\) with respect to \(p\) is as follows:

$$\begin{aligned} \frac{{\partial^{2} \varPi_{A} }}{{\partial p^{2} }} & = - \left[ {\frac{{\rho D^{\prime\prime}\left( p \right)}}{{t_{1}^{*} + t_{2}^{*} }}\left\{ {\left( { - p + C_{\text{l}} + C} \right)\left( {\int\limits_{0}^{{t_{1}^{*} }} {\beta \left( {t_{1}^{*} - t} \right){\text{d}}t} } \right) + C_{\text{b}} \int\limits_{0}^{{t_{1}^{*} }} {\left( {\int\limits_{0}^{t} {\beta \left( {t_{1}^{*} - x} \right){\text{d}}x} } \right){\text{d}}t} } \right.} \right. \\ & \quad \left. { + C_{\text{h}} \left( {\int\limits_{0}^{{t_{2}^{*} }} {\int\limits_{t}^{{t_{2}^{*} }} {e^{{\left( {1 - m\left( \xi \right)} \right)\left( {g\left( x \right) - g\left( t \right)} \right)}} {\text{d}}x{\text{d}}t} } } \right) - pt_{2}^{*} + C_{\text{l}} t_{1}^{*} + C\int\limits_{0}^{{t_{2}^{*} }} {e^{{\left( {1 - m\left( \xi \right)} \right)g\left( x \right)}} {\text{d}}x} } \right\} - \frac{2\rho D'\left( p \right)}{{t_{1}^{*} + t_{2}^{*} }}\left\{ {t_{2}^{*} + \int\limits_{0}^{{t_{1}^{*} }} {\beta \left( {t_{1}^{*} - t} \right)} {\text{d}}t} \right\} \\ & \quad \left. { + \frac{{K\alpha \left( {\rho - 1} \right)^{2} \left[ {\left( {t_{1}^{*} + t_{2}^{*} } \right)\left( {D\left( p \right) + \varepsilon } \right)} \right]^{\alpha - 1} \left[ {\left( {D\left( p \right) + \varepsilon } \right)D^{\prime\prime}\left( p \right) + \left( {D^{\prime}\left( p \right)} \right)^{2} \left( {\alpha - 1} \right)} \right]}}{D\left( p \right) + \varepsilon }} \right]. \\ \end{aligned}$$
(28)

It is clear that \(\frac{{\partial^{2} \varPi_{\rm A} }}{{\partial p^{2} }} < 0\). Consequently, \(\varPi_{\rm A}\) is a strictly concave function of \(p\). Thus, \(p^{*}\) is the optimal selling price that maximizes the total profit function \(\varPi_{\rm A} \left( {t_{1}^{*} ,t_{2}^{*} ,p,\xi } \right)\) for fixed \(t_{1}^{*} ,t_{2}^{*}\) and \(\xi\).

Now, the first and second partial derivatives of the profit function \(\varPi_{\rm A} \left( {t_{1}^{*} ,t_{2}^{*} ,p^{*} ,\xi } \right)\) with respect to \(\xi\) are as follows:

$$\begin{aligned} \frac{{\partial \varPi_{\rm A} }}{\partial \xi } & = - \frac{{\rho \left( {D\left( {p^{*} } \right) + \varepsilon } \right)}}{{t_{1}^{*} + t_{2}^{*} }}\left\{ {C_{\text{h}} \int\limits_{0}^{{t_{2}^{*} }} {\int\limits_{t}^{{t_{2}^{*} }} {m^{\prime}\left( \xi \right)\left[ {g\left( t \right) - g\left( x \right)} \right]} \exp \left[ { - \left( {1 - m\left( \xi \right)} \right)\left( {g\left( t \right) - g\left( x \right)} \right)} \right]{\text{d}}x{\text{d}}t} } \right. \\ & \quad \left. { + C\int\limits_{0}^{{t_{2}^{*} }} {m^{\prime}\left( \xi \right)\left[ {g\left( x \right)} \right]\exp \left[ { - \left( {1 - m\left( \xi \right)} \right)g\left( x \right)} \right]dx - t_{1}^{*} - t_{2}^{*} } } \right\}, \\ \end{aligned}$$
(29)
$$\begin{aligned} \frac{{\partial^{2} \varPi_{A} }}{{\partial \xi^{2} }} & = - \frac{{\rho \left( {D\left( {p^{*} } \right) + \varepsilon } \right)}}{{t_{1}^{*} + t_{2}^{*} }}\left\{ {C_{\text{h}} \int\limits_{0}^{{t_{2}^{*} }} {\int\limits_{t}^{{t_{2}^{*} }} {\exp \left[ { - \left( {1 - m\left( \xi \right)} \right)\left( {g\left( t \right) - g\left( x \right)} \right)} \right]} \left\{ {m^{\prime\prime}\left( \xi \right)\left( {g\left( t \right) - g\left( x \right)} \right)} \right.} } \right. \\ & \quad + \left[ {m^{\prime}\left( \xi \right)\left( {g\left( t \right) - g\left( x \right)} \right)} \right]^{2} {\text{d}}x{\text{d}}t + C\int\limits_{0}^{{t_{2}^{*} }} {\left\{ {m^{\prime\prime}\left( \xi \right)g\left( x \right)\exp \left[ {\left( {1 - m\left( \xi \right)} \right)g\left( x \right)} \right]} \right.} \\ & \quad \left. {\left. { + \left[ {m^{\prime}\left( \xi \right)g\left( x \right)} \right]^{2} \exp \left[ {\left( {1 - m\left( \xi \right)} \right)g\left( x \right)} \right]} \right\}} \right\}. \\ \end{aligned}$$
(30)

It is clear from the above equation that \(\frac{{\partial^{2} \varPi_{A} }}{{\partial \xi^{2} }}\) is negative. Hence, the total profit function is a concave function of the preservation technology cost \(\left( \xi \right)\). Therefore, \(\left( {\xi^{*} } \right)\) is the optimal preservation technology cost that maximizes the total profit per unit function for fixed \(t_{1}^{*} ,t_{2}^{*}\) and \(p^{*}\).

Numerical examples and sensitivity analysis

Example 1

To illustrate the solution procedure, we consider an inventory situation with following data: A = $120/unit, C = $20/unit, \(C_{\text{h}}\) = $3/unit/year, \(C_{\text{b}}\) = $4/unit/year, \(C_{\text{l}}\) = $5/unit, \(\mu\) = 20, \(\rho\) = 2, K = 5, \(\alpha\) = 1, \(\theta \left( t \right)\) = 0.2 + 0.1t, \(d\left( p \right) = \alpha_{1} - p\beta_{1} = 350 - 2.5p\), \(\beta \left( x \right) = \frac{1}{1 + 2x}\), the reduced deterioration rate is \(m\left( \xi \right) = 1 - {\text{e}}^{ - a\xi }\), \(a \ge 0\), we set \(a\) = 0.01 and constraint of preservation technology cost w = 100.

With the given data, the optimal solution is found using MAPLE 18 software. The optimum results are: \(t_{1}^{*}\) = 0.1747, \(t_{2}^{*}\) = 0.2942, \(p^{*}\) = 85.8307, \(\xi^{*}\) = 61.72, \(\varPi_{\rm A}^{*}\) = 18,859.90 and \(Q^{*}\) = 66.71.

Next, we consider distinct values of \(\xi\) = 0, 30, 60… 300 to examine the behaviour of total profit function. The numerical results are presented in Table 1. The numerical results of Table 1 show that increasing the preservation technology investment results in an increase in the order quantity, while the feasible limit of preservation technology cost leads to increase in total profit per unit time. Whereas the total profit increases up to some extent and then decreases subsequently.

Table 1 Computational results for different values of ξ
Full size table

Table 2 shows the optimal results for different values of the shape parameter \(\left( a \right)\) of the function \(m\left( \xi \right)\) with the above stated values of the other model parameters. The results reveal that as a increases, optimal shortage period \(\left( {t_{1}^{*} } \right),\) optimal selling price \(\left( {p^{*} } \right)\) and optimal preservation technology cost \(\left( {\xi^{*} } \right)\) decreases whereas optimal inventory period \(\left( {t_{2}^{*} } \right)\), optimal total profit per unit \(\left( {\varPi_{\rm A}^{*} } \right)\) and optimal ordering quantity \(\left( {Q^{*} } \right)\) increase which is quite rational.

Table 2 Computational results for different values of a
Full size table

Example 2

The same set of data is considered as in the Example 1 except putting \(\beta \left( x \right) = {\text{e}}^{{ - \left( {\delta x} \right)}}\). From Example 1, we find that \(\varPi_{A} \left( {t_{1} ,t_{2} ,p,\xi } \right)\) reaches its maximum at \(\xi\) = 61.72 and by (6) and (7), we get \(t_{1}^{*}\) = 0.01716, \(t_{2}^{*}\) = 0.2967, \(p^{*}\) = 85.8347, \(\xi^{*}\) = 98.4092, \(Q^{*}\) = 69.99 and \(\varPi_{\rm A}^{*}\) = 18,823.94.

Example 3

We investigate the effects of changes in the value of promotional effort (\(\rho\)) and scaling parameter (K) on optimal solution. The identical set of input data are as in Example 1. The optimal solution for different values of \(\rho\) and K is summarized in Table 3.

Table 3 Computational results for different values of ρ and K
Full size table

From Table 3, it can be observed that for promotional effort \(\left( \rho \right)\) increases, optimal selling price \(\left( {p^{*} } \right)\), optimal preservation technology cost \(\left( {\xi^{*} } \right)\), optimal total profit per unit \(\left( {\varPi_{A}^{*} } \right)\) and optimal order quantity \(\left( {Q^{*} } \right)\) increase, while optimal shortage period (\(t_{1}^{*}\)) and optimal inventory period (\(t_{2}^{*}\)) decrease. These results reveal that if the retailer encourages promotional activity which increases the demand of the product and thereby increase the total profit significantly.

On the other hand, as the value of scaling parameter \(\left( K \right)\) increases, optimal inventory period \(\left( {t_{2}^{*} } \right)\) and optimal selling price \(\left( {p^{*} } \right)\) increase, while optimal shortage period \(\left( {t_{1}^{*} } \right)\), optimal preservation technology cost \(\left( {\xi^{*} } \right)\), optimal total profit per unit \(\left( {\varPi_{A}^{*} } \right)\), and optimal ordering quantity (\(Q^{*}\)) decrease.

Example 4

In this example, we study the effect of constant parameter (\(\alpha_{1}\)) and scaling parameter (\(\beta_{1}\)) on the optimal solution. The same set of input data are considered as in Example 1. Computational results are summarized in Table 4 for various set of values of parameters \(\alpha_{1} \in\) {180, 240, 300, 360, 420} and \(\beta_{1}\) ∈ {1.62, 2.16, 2.7, 3.24, 3.78}.

Table 4 Computational results for different values of demand parameters
Full size table

Based on the computational results shown in Table 4, we can observe that the optimal selling price (\(p^{*}\)), optimal preservation technology (\(\xi^{*}\)), optimal ordering quantity (\(Q^{*}\)), and optimal total profit (\(\varPi_{A}^{*}\)) increase with an increase while optimal shortage period (\(t_{1}^{*}\)) and optimal inventory period (\(t_{2}^{*}\)) decrease with an increase in the value of constant parameter (\(\alpha_{1}\)). These results imply that as constant parameter \(\left( {\alpha_{1} } \right)\) of the demand function increases with the total profit increases drastically.

On the other hand, we can observe that the optimal shortage period \(\left( {t_{1}^{*} } \right)\), optimal inventory period \(\left( {t_{2}^{*} } \right)\), and optimal ordering quantity \(\left( {Q^{*} } \right)\) increase with an increase in the value of scaling parameter (\(\beta_{1}\)). Apparently, the reduction in the value of optimal selling price \(\left( {p^{*} } \right)\), optimal preservation technology cost \(\left( {\xi^{*} } \right)\) and optimal total profit \(\left( {\varPi_{A}^{*} } \right)\) found with an increase in the value of scaling parameter (\(\beta_{1}\)). Obviously, the demand rate decreases as the value of \(\left( {\beta_{1} } \right)\) increases. This result reveals that scaling parameter \(\beta_{1}\) increases in demand function which decreases the demand. Therefore, there will be decrease in total profit.

Example 5

This example presents the impact of random variable \(E\left( \varepsilon \right) = \mu\) on optimal solution. We considered the same set of input data as in Example 1. The optimal solution for different values of random variable (\(\mu\)) is summarized in Table 5.

Table 5 Computational results for different distribution of ε
Full size table

The results of Table 5 reveal that as optimal selling price \(\left( {p^{*} } \right)\), optimal preservation technology cost \(\left( {\xi^{*} } \right)\), optimal total profit \(\left( {\varPi_{\rm A}^{*} } \right)\), and optimal ordering quantity \(\left( {Q^{*} } \right)\) increase, while optimal shortage period \(\left( {t_{1}^{*} } \right)\) and optimal inventory period \(\left( {t_{2}^{*} } \right)\) decrease with an increase in the value of random variable \(\left( \varepsilon \right)\). Table 5 displays the results for different normal distribution, uniform distribution, and exponential distribution function parameters of random variable. Obviously, the demand increases as the value of mean \(\left( \mu \right)\) increases. With the increase in demand rate, retailer increases ordering quantity of product as well as preservation technology cost to reduce the deterioration rate. Consequently, the increased demand enhances the total profit which is quite rational.

Conclusions

In this paper, a shortage followed by inventory model for a joint pricing, inventory, and preservation decision for deteriorating items is presented. The demand is characterized as stochastic and depend on price which is further influenced by promotional effort and expressed by mark-up over the promotional effort. In model formulation, the utilization of general time proportional deterioration and partial backlogging rates makes the scope of the application broader. Moreover, the analysis of objective function with rational and exponential partial backlogging is carried out and some useful results on finding the optimal replenishment are derived. Furthermore, to illustrate the model numerical examples together with some managerial implications by varying the values of key parameters are provided. The numerical results succinctly demonstrated the importance of promotional effort. In addition, an improvement in total profit by investing in preservation technology is explained.

For future research, this model can be extended for multi item EOQ model, trade credit policy, a finite replenishment rate, and so forth. It would be interesting to study the model under supply chain settings.