Introduction

Data envelopment analysis (DEA) is one of the approaches that has been widely applied to evaluate the performance of decision-making units (DMUs) (Charnes et al. 1978). Using this approach, the efficiency of DMUs can be evaluated in different cases. For example, data may be discretionary or non-discretionary (see, e.g., Tohidi and Razavyan 2010). Furthermore, it is possible that the input cost and/or the output price vectors are known (see, e.g., Tohidi and Khodadadi 2013). Other applications have also been presented in Shafiee et al. (2016) and Shokrollahpour et al. (2016).

In some cases, the DMUs may be formed from more than one process. In such cases, an approach labeled network DEA approach can be used to study the internal structure of such DMUs (Fare and Grosskopf 2000; Fare et al. 2007). In the special cases, network system may have two-stage structure. Many approaches are presented to model the performance of this type of system. Chen et al. (2009) developed additive efficiency decomposition and expressed the overall efficiency of such DMUs as a weighted sum of the efficiencies of the two individual processes. Liang et al. (2008) decomposed efficiency of such a system using the game approach for the case that the second stage consumes only the intermediate products produced by the first stage. Li et al. (2012) presented two models to evaluate the performance of a two-stage system that its second stage consumes both the outputs generated by the first stage and additional inputs to the second stage. Yu and Qinfen (2014) proposed a two-stage DEA model with additional input in the second stage and part of intermediate products as final outputs. In addition, Khalili-Damghani et al. (2012) proposed a fuzzy two-stage data envelopment analysis (FTSDEA) which its Mathematical modeling results in great reduction of computational efforts. Network systems have many applications. For instance, Lozano et al. (2013) proposed a directional distance approach and applied it to model airport operations. They assume that the processes may generate both desirable and undesirable outputs. Other applications have been informed in Fukuyama and Matousek (2011), Yu (2010), Zhu (2011). To measure the technical and cost efficiencies of general network systems with \(q\;(q \ge 2)\) processes connected in series in a specified period of time, Lozano (2011) proposed a relational DEA model and a minimum cost network DEA model, respectively. When DMUs are observed in \(T(T > 1)\) periods of time, we will have multi-period technical and cost efficiencies. In this framework, Kao and Hwang (2014) proposed a multi-period DEA model to measure the overall performance of a two-stage production system that is a special case of networks of processes. For more study in the field of multi-period systems, see also Esmaeilzadeh and Hadi-Vencheh (2013), Kao and Liu (2013).

Fare et al. (1989) applied the DEA approach to compute the Malmquist productivity index. Malmquist index was first introduced by Caves et al. (1982) and can be used to evaluate the productivity change over time. Pastor and Lovell (2005) extended the Malmquist index to the global Malmquist index that was defined based on the global production technology. Maniadakis and Thanassoulis (2004) proposed the cost Malmquist productivity index for analyzing the productivity change between two time periods when the input prices are known. To define the index, they used the cost efficiency of the under evaluation DMU. The concept of cost inefficiency has also been used in Lin et al. (2017) to define a cost Luenberger productivity indicator. Following Maniadakis and Thanassoulis (2004), Tohidi et al. (2008) used the concept of the profit efficiency and presented the profit Malmquist productivity index. They assumed that the costs of inputs and the prices of outputs are known simultaneously. Tohidi et al. (2012) introduced the global cost efficiency and to define this efficiency used a common input price vector. Based on the global cost efficiency, the global cost Malmquist productivity index was introduced to measure the productivity changes of the DMUs between two time periods when the prices of the inputs are at hand (Tohidi et al. 2012). Their proposed index is circular, its adjacent period components provides a single measure of productivity change and also LP infeasibility cannot occur. The common input price vector can be obtained by solving a model introduced in Tohidi et al. (2013). See also Khalili-Damghani and Hosseinzadeh lotfi (2012) as another application of Malmquiat productivity index.

This paper proposes a multi-period DEA model to examine the performance of networks of processes observed in T time periods. By considering a subsystem corresponding to each period, we have network system with a parallel structure of T subsystem where each subsystem has q processes connected in series. Using the proposed multi-period DEA model and also the mathematical relationships between the global cost efficiencies of the total system, its subsystems and its processes, we measure the multi-period global cost efficiency of network system in three different ways. In fact, the operation of each process or each subsystem takes into account in measuring the global cost efficiency of the multi-period network system. We consider the processes of the system as the independent units and measure the multi-period global cost efficiencies of them, then we calculate the multi-period global cost efficiency of network system using a weighted average of the obtained global cost efficiencies of the processes. Also, we show that the multi-period global cost efficiency of the network system can be defined as a weighted average of the subsystem global cost efficiencies.

Using the proposed models, we define the global cost Malmquist productivity index and apply it for measuring the productivity changes of network system between two periods of time. The index is similar to the global cost Malmquist index introduced in Tohidi et al. (2012), but we eliminate the common input price vector and use the real input prices of time periods. This index has the circularity property. Also, using the global production technology the models that are used for computing the index are always feasible. This paper also presents a productivity index with aggregate structure in a way that the productivity changes of network system can be defined as a weighted average of the process productivity changes. Using this property, decision makers can identify the most effective processes in the productivity changes of network system.

This paper is organized as follows. In “Cost efficiency analysis” section, the global cost efficiency of network system is calculated. “Relationship between the global cost efficiencies of multi-period network system and its subsystems” and “Relationship between the multi-period global cost efficiencies of network system and its processes” sections compute the global cost efficiencies of the subsystems and processes and represent the relationships between these efficiencies and the efficiency of network system. In “Productivity change” section, the productivity change of network system is computed in two different ways. “Numerical example” section presents a numerical example. “Conclusion” section concludes.

Cost efficiency analysis

Consider a set of n DMUs observed in T different time periods. Each DMU has q processes. Interrelationships among the processes are the same for all DMUs. Let \(I(p)\) and \(O(p)\) denote the sets of the exogenous inputs and final outputs for process p, \((p = 1, \ldots ,q)\), of \({\text{DMU}}_{j}\), \((j = 1, \ldots ,n)\), respectively. Assume that \(x_{ij}^{pt}\) denote the level of the exogenous input \(i,\,(i = 1, \ldots ,m),\) used by process p of \({\text{DMU}}_{j}\) in time period \(t,\,(t = 1, \ldots ,T)\). Thus, \(x_{ij}^{t} = \sum_{{p \in P_{I} (i)}} {x_{ij}^{pt} }\) is the total amount of exogenous input \(i\) used by all processes of DMUj in period \(t\), where \(P_{I} (i)\) denotes the set of processes that use the exogenous input i, and \(x_{ij}^{p} = \sum_{t = 1}^{T} {x_{ij}^{pt} }\) is the total amount of exogenous input i that the process p of DMUj consumes in T time periods. Similarly, \(y_{kj}^{pt}\) denotes the level of final output \(k,\,(k = 1, \ldots ,s)\), produced by process p of DMUj in time period t. The term \(y_{kj}^{t} = \sum_{{p \in P_{O} (k)}} {y_{kj}^{pt} }\) is the total amount of final output k, produced by all processes of DMUj in period t, where \(P_{O} (k)\) denotes the set of processes that produce the final output k. Moreover, the term \(y_{kj}^{p} = \sum\nolimits_{t = 1}^{T} {y_{kj}^{pt} }\) is the total amount of final output k produced by process p in T time periods. Finally, the total amount of exogenous input i consumed by all processes of DMUj after T periods and the total amount of final output k produced by all processes of DMUj after T time periods are, respectively, as follows:

$$\begin{aligned} x_{ij}^{{}} = \sum\limits_{t = 1}^{T} {x_{ij}^{t} = \sum\limits_{{p \in P_{I} (i)}} {x_{ij}^{p} ,} } \hfill \\ y_{kj}^{{}} = \sum\limits_{t = 1}^{T} {y_{kj}^{t} = \sum\limits_{{p \in P_{O} (k)}} {y_{kj}^{p} .} } \hfill \\ \end{aligned}$$
(1)

In addition to the mentioned assumption, suppose that there are \(R\) intermediate products that are produced by a stage of the system and then become the inputs to the next stages. \(P_{in} (r)\) and \(P_{out} (r)\) denote the sets of processes that consume and produce the intermediate product r, respectively. In other words, the intermediate product \(r\) is an input for each p, \(p \in P_{in} (r)\), and an output for each p, p ∈ Pout(r). Similarly, the sets \(R^{out} (p)\) and \(R^{in} (p)\) are the intermediate products, produced and consumed by process p, respectively. We consider z pt rj as the amount of product r produced by the process p, p ∈ Pout(r), or consumed by the process p, \(p \in P_{in} (r)\), in time period t. We assume that the total amount of product r consumed by all processes of DMUj in the period t is equal to the total amount of this product produced by all processes of DMUj at the same time period.

Based on the definition of the production possibility set (PPS) of process p, (p = 1,…, q) in Lozano (2011), we consider the PPS of process p in time period t, (t = 1,…, T) as:

$$T_{p}^{t} = \left\{ {(x_{i}^{pt} ,y_{k}^{pt} ,z_{r}^{pt} )\left| \begin{aligned} &\exists \lambda_{j}^{pt} \in \varLambda_{p}^{t} {\kern 1pt} \forall j\,\,x_{i}^{pt} \ge \sum\limits_{j} {\lambda_{j}^{pt} x_{ij}^{pt} \,\forall i \in I(p)\quad y_{k}^{pt} \le \sum\limits_{j} {\lambda_{j}^{pt} y_{kj}^{pt} \,\forall k \in O(p){\kern 1pt} } } \hfill \\& z_{r}^{pt} \ge \sum\limits_{j} {\lambda_{j}^{pt} z_{rj}^{pt} {\kern 1pt} {\kern 1pt} \forall r \in R^{in} (p)\;\;\;z_{r}^{pt} \le \sum\limits_{j} {\lambda_{j}^{pt} z_{rj}^{pt} {\kern 1pt} {\kern 1pt} \forall r \in R^{out} (p)\;\;\;} \;} \hfill \\ \end{aligned} \right.} \right\}.$$
(2)

The set \(\varLambda_{p}^{t}\) represents the returns to scale (RTS) assumption for process p in time period \(t\). Thus, \(\varLambda_{p}^{CRS} = \left\{ {\left. {\lambda_{j}^{pt} } \right|\lambda_{j}^{pt} \ge 0\;\forall j\,} \right\}\) and \(\varLambda_{p}^{VRS} = \left\{ {\left. {\lambda_{j}^{pt} } \right|\lambda_{j}^{pt} \ge 0\;\forall j\,\;\sum\nolimits_{j} {\lambda_{j}^{pt} = 1} } \right\}\) correspond to CRS and VRS, respectively. According to the definition of the PPS of the system in Lozano (2011), we consider the PPS of the system in time period t (we call it subtechnology) as:

$$T_{{}}^{t} = \left\{ {(x_{i}^{t} ,y_{k}^{t} )\left| \begin{aligned} &\exists {\kern 1pt} (x_{i}^{pt} ,y_{k}^{pt} ,z_{r}^{pt} ) \in T_{p}^{t} \;\,\forall p\,\,x_{i}^{t} \ge \sum\limits_{{p \in P_{I} (i)}} {x_{ij}^{pt} \,\;\forall i\quad y_{k}^{t} \le \sum\limits_{{p \in P_{O} (k)}} {y_{kj}^{pt} \,\;\forall k{\kern 1pt} } } \hfill \\ &\sum\limits_{{p \in P_{out} (r)}} {z_{rj}^{pt} {\kern 1pt} {\kern 1pt} - \sum\limits_{{p \in P_{in}^{{}} (r)}} {z_{rj}^{pt} } \ge 0\;\;\forall r\;\;\;\;} \hfill \\ \end{aligned} \right.} \right\}.$$
(3)

Following the definition of \(T^{t}\), we define the system global PPS (the network technology) as the composition of the subtechnologies \(T^{t}\), \((t = 1, \ldots ,T),\)

$$T = \left\{ {(x_{i}^{{}} ,y_{k}^{{}} )\left| \begin{aligned}& \exists {\kern 1pt} (x_{i}^{t} ,y_{k}^{t} ,z_{r}^{t} ) \in T_{{}}^{t} \;\,\forall t\,\,\,x_{i}^{{}} \ge \sum\limits_{t} {\sum\limits_{{p \in P_{I} (i)}} {x_{ij}^{pt} } } \;\forall i\quad y_{k}^{{}} \le \sum\limits_{t} {\sum\limits_{{p \in P_{O} (k)}} {y_{kj}^{pt} \,\;\forall k{\kern 1pt} } } \hfill \\ & \sum\limits_{t} {\sum\limits_{{p \in P_{out}^{{}} (r)}} {z_{rj}^{pt} } } - \sum\limits_{t} {\sum\limits_{{p \in P_{in}^{{}} (r)}} {z_{rj}^{pt} } \ge 0\;\;\forall r} \hfill \\ \end{aligned} \right. } \right\}.$$
(4)

Consider \(c^{t} = (c_{1}^{t} ,c_{2}^{t} , \ldots ,c_{m}^{t} )\) as the price vector of exogenous inputs in time period t. Since the intermediate products consumed by the processes of DMUs are completely produced within the system, it is reasonable to assign the zero value as the price of each product in time period t. It is clear that the system global PPS \(T\) is formed from data of all DMUs in all time periods and because the input prices vary between time periods, thus the global PPS includes DMUs with different input prices. Therefore, to avoid the unacceptable results (Tone 2002), we define a cost-based global PPS (Cooper et al. 2006) as:

$$\bar{T} = \left\{ {(\bar{x}_{i}^{{}} ,y_{k}^{{}} )\left| \begin{aligned}& \exists {\kern 1pt} (\bar{x}_{i}^{t} ,y_{k}^{t} ,z_{r}^{t} ) \in T_{{}}^{t} \;\,\forall t\,\,\,\bar{x}_{i}^{{}} \ge \sum\limits_{t} {\sum\limits_{{p \in P_{I} (i)}} {\bar{x}_{ij}^{pt} } } \;\forall i\quad y_{k}^{{}} \le \sum\limits_{t} {\sum\limits_{{p \in P_{O} (k)}} {y_{kj}^{pt} \,\;\forall k{\kern 1pt} } } \hfill \\ & \sum\limits_{t} {\sum\limits_{{p \in P_{out}^{{}} (r)}} {z_{rj}^{pt} } } - \sum\limits_{t} {\sum\limits_{{p \in P_{in}^{{}} (r)}} {z_{rj}^{pt} } \ge 0\;\;\forall r} \hfill \\ \end{aligned} \right.} \right\}.$$
(5)

where \(\bar{x}_{ij}^{pt} = c_{i}^{t} x_{ij}^{pt} \,(\forall (i,j,p,t))\).

Now, based on the global PPS \(\bar{T}\), we compute the minimum cost for producing a given final output vector \(y_{o}^{{}} = (y_{1o}^{{}} ,y_{2o}^{{}} , \ldots ,y_{so}^{{}} )\) defined in (1) by a network DEA model as follows:

$$\begin{aligned} &C_{o} = \hbox{min} \quad \sum\limits_{i = 1}^{m} {\bar{x}_{i}^{{}} } \hfill \\ & {\text{s}} . {\text{t}} . { }\quad\sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{I} (i)}}^{{}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{pt} \bar{x}_{ij}^{pt} } } } \le \bar{x}_{i}^{{}}, \quad i = 1, \ldots ,m, \hfill \\ & \qquad \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{O} (k)}}^{{}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{pt} y_{kj}^{pt} } } } \ge y_{ko}^{{}} ,\quad k = 1, \ldots ,s, \hfill \\ & \qquad\sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{out} (r)}}^{{}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{pt} z_{rj}^{pt} } - } } \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{in} (r)}}^{{}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{pt} z_{rj}^{pt} } } } \ge 0,\quad r = 1, \ldots ,R, \hfill \\ & \qquad\lambda_{j}^{pt} \ge 0,\quad t = 1, \ldots ,T, \, j = 1, \ldots ,n, \quad p = 1, \ldots ,q, \hfill \\ &\qquad \bar{x}_{i}^{{}} \ge 0,\quad \, i = 1, \ldots ,m. \hfill \\ \end{aligned}$$
(6)

By the optimal solution to model (6), the target operation point for \({\text{DMU}}_{o}\) can be written as:

$$\hat{\bar{x}}_{i} = \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{I} (i)}}^{{}} {\sum\limits_{j = 1}^{n} {(\lambda_{j}^{pt} )^{*} \bar{x}_{ij}^{pt} } } } ,\quad i = 1, \ldots ,m.$$
(7)

\(\hat{\bar{x}}_{i}\), obtained by the optimal solution of model (6), is the projection of ith input for DMUo after T time periods. Thus, the multi-period global cost efficiency of DMUo after T time periods can be computed as:

$$CE_{o} = \frac{{C_{o} }}{{\sum_{i = 1}^{m} {\bar{x}_{io}^{{}} } }}.$$
(8)

Theorem 1

Model (6) is always feasible.

Proof

Based on the formulation (1), we have

$$\begin{aligned} \bar{x}_{io} & = \sum\limits_{t = 1}^{T} {\bar{x}_{io}^{t} = \sum\limits_{{p \in P_{I} (i)}} {\bar{x}_{io}^{p} = \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{I} (i)}}^{{}} {\bar{x}_{io}^{pt} } } ,} } \quad \bar{x}_{io}^{pt} = c_{i}^{t} x_{io}^{pt} \,\left( {\forall i,p,t} \right), \\ y_{ko} & = \sum\limits_{t = 1}^{T} {y_{ko}^{t} = \sum\limits_{{p \in P_{O} (k)}} {y_{ko}^{p} = \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{O} (k)}}^{{}} {y_{ko}^{pt} } } .} } \\ \end{aligned}$$

On the basis of the definition of the system global PPS \(\bar{T}\), the under evaluation DMU is in principle feasible by T. In fact, DMUo always belongs to \(\bar{T}\). Therefore, model (6) will be always feasible. The model has a feasible solution as follows:

$$\lambda_{o}^{pt} = 1,\,\lambda_{j}^{pt} = 0{\kern 1pt} \,\left( {j \ne o} \right),\;\left( {\forall t,\forall p} \right),\;\bar{x}_{i}^{{}} = \bar{x}_{io}^{{}} \;\left( {\forall i} \right).$$

Relationship between the global cost efficiencies of multi-period network system and its subsystems

When model (6) is used to measure the multi-period global cost efficiency of network system, because the operations of individual periods are ignored, the multi-period network system may be identified as an efficient DMU, although every period is inefficient. In this case, the obtained results are unreasonable. For this reason, we propose another approach to measure the multi-period global cost efficiency of \({\text{DMU}}_{o}\) in a way that solves this problem.

To calculate the global cost efficiency of the subsystem \(t = l,\,(l = 1, \ldots ,T)\), of multi-period network system (the global cost efficiency of DMUo in time period \(l\) or period global cost efficiency), we first revise model (6) as follows:

$$\begin{aligned} &C_{o}^{l} = \hbox{min} \quad \sum\limits_{i = 1}^{m} {\bar{x}_{i}^{l} } \hfill \\ {\text{s}} . {\text{t}} . { }& \quad \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{I} (i)}}^{{}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{pt} \bar{x}_{ij}^{pt} } } } \le \bar{x}_{i}^{l},\quad i = 1, \ldots ,m, \hfill \\ & \quad \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{O} (k)}}^{{}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{pt} y_{kj}^{pt} } } } \ge y_{ko}^{l} , \quad k = 1, \ldots ,s, \hfill \\ & \quad \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{out} (r)}}^{{}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{pt} z_{rj}^{pt} } - } } \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{in} (r)}}^{{}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{pt} z_{rj}^{pt} } } } \ge 0,\quad r = 1, \ldots ,R, \hfill \\ & \quad \lambda_{j}^{pt} \ge 0, \quad t = 1, \ldots ,T, \; j = 1, \ldots ,n,\quad p = 1, \ldots ,q, \hfill \\ & \quad \bar{x}_{i}^{l} \ge 0,\quad i = 1, \ldots ,m. \hfill \\ \end{aligned}$$
(9)

The value of \(C_{o}^{l}\) is the minimum cost of producing a given final output vector \(y_{o}^{l} = (y_{1o}^{l} ,y_{2o}^{l} , \ldots ,y_{so}^{l} )\). By the optimal solution to model (9), the target operation point for subsystem \(l\) will be as:

$$\hat{\bar{x}}_{i}^{l} = \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{I} (i)}}^{{}} {\sum\limits_{j = 1}^{n} {(\lambda_{j}^{pt} )^{*} \bar{x}_{ij}^{pt} } } } ,\quad i = 1, \ldots ,m.$$
(10)

Therefore, the global cost efficiency of the subsystem \(l\) can be computed as:

$$CE_{o}^{l} = \frac{{C_{o}^{l} }}{{\sum_{i = 1}^{m} {\bar{x}_{io}^{l} } }} = \frac{{\sum_{i = 1}^{m} {\hat{\bar{x}}_{i}^{l} } }}{{\sum_{i = 1}^{m} {\sum\limits_{{p \in P_{I} (i)}}^{{}} {\bar{x}_{io}^{pl} } } }}.$$
(11)

After solving model (9) for each time period \(t = l,\,(l = 1, \ldots ,T)\), we calculate the global cost efficiency of multi-period network system, this time by using the obtained optimal solutions to model (9) as follows:

$$CE_{o}^{\prime } = \frac{{\sum_{l = 1}^{T} {C_{o}^{l} } }}{{\sum_{t = 1}^{T} {\sum_{i = 1}^{m} {\bar{x}_{io}^{t} } } }}.$$
(12)

In fact, \(CE_{o}^{\prime }\) is defined as the ratio of the aggregate minimum cost of \(T\) subsystems to the observed aggregate cost for multi-period network system.

It is noteworthy that, since the multi-period network system has a parallel structure of \(T\) subsystems, the system global cost efficiency can be expressed as a weighted average of the T subsystem global cost efficiencies by \(w^{l}\) (Kao 2009a,b; Kao and Hwang 2010):

$$CE_{o}^{\prime } = \sum\limits_{l = 1}^{T} {w^{l} } CE_{o}^{l} ,\quad w^{l} = \frac{{\sum_{i = 1}^{m} {\sum_{{p \in P_{I} (i)}}^{{}} {\bar{x}_{io}^{pl} } } }}{{\sum_{t = 1}^{T} {\sum_{i = 1}^{m} {\bar{x}_{io}^{t} } } }}.$$
(13)

The weight \(w^{l}\) represents contribution of the observed cost of period l (that is the total cost of exogenous inputs consumed by all processes of subsystem l) to the observed cost of all periods (total cost of the multi-period system). In fact, the observed amount of the cost of a subsystem reflects its importance.

Relationship between the multi-period global cost efficiencies of network system and its processes

Similarly, because the operations of individual processes are ignored, the multi-period network system may be identified as an efficient DMU after T time periods, although every process is inefficient. For this reason, we first calculate the global cost efficiency of process \(p = \alpha ,\,(\alpha = 1, \ldots ,q),\) of DMUo after T time periods (process multi-period global cost efficiency) as follows:

$$CE_{o}^{\alpha } = \frac{{C_{o}^{\alpha } }}{{\sum_{i \in I(\alpha )} {\bar{x}_{io}^{\alpha } } }} = \frac{{\sum_{i \in I(\alpha )} {\hat{\bar{x}}_{io}^{\alpha } } }}{{\sum_{t = 1}^{T} {\sum_{i \in I(\alpha )} {\bar{x}_{io}^{\alpha t} } } }},$$
(14)

where \(C_{o}^{\alpha }\) is the minimum cost of producing a given final output vector \(y_{o}^{\alpha } = (y_{1o}^{\alpha } ,y_{2o}^{\alpha } , \ldots ,y_{so}^{\alpha } )\) and \(\hat{\bar{x}}_{io}^{\alpha } = \sum\nolimits_{t = 1}^{T} {\hat{\bar{x}}_{io}^{\alpha t} }\) is the target operation point for the ith input of the process \(\alpha\) after T time periods. More precisely, \(C_{o}^{\alpha }\) and \(\hat{\bar{x}}_{io}^{\alpha } ,(\alpha = 1, \ldots ,q)\) can be computed as follows:

$$\begin{aligned} C_{o}^{\alpha } & = \hbox{min} \quad \sum\limits_{i \in I(\alpha )}^{{}} {\bar{x}_{i}^{\alpha } } \\ {\text{s}} . {\text{t}} .& \, \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{I} (i)}}^{{}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{pt} \bar{x}_{ij}^{pt} } } } \le \bar{x}_{i}^{\alpha } ,\,\quad i \in I(\alpha ), \\ & \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{O} (k)}}^{{}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{pt} y_{kj}^{pt} } } } \ge y_{ko}^{\alpha } ,\quad k = 1, \ldots ,s, \\ & \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{out} (r)}}^{{}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{pt} z_{rj}^{pt} } - } } \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{in} (r)}}^{{}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{pt} z_{rj}^{pt} } } } \ge 0,\quad r = 1, \ldots ,R, \\ & \lambda_{j}^{pt} \ge 0,\quad t = 1, \ldots ,T,j = 1, \ldots ,n,\,\,p = 1, \ldots ,q, \\ & \bar{x}_{i}^{\alpha } \ge 0,\quad i \in I(\alpha ), \\ \end{aligned}$$
(15)
$$\hat{\bar{x}}_{i}^{\alpha } = \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{I} (i)}}^{{}} {\sum\limits_{j = 1}^{n} {(\lambda_{j}^{pt} )^{*} \bar{x}_{ij}^{pt} } } } ,\quad i \in I(\alpha ).$$
(16)

By the optimal solutions to model (15) for \(\alpha = 1, \ldots ,q,\) we can calculate the multi-period global cost efficiency of network system and its processes at the same time. We define the multi-period system global cost efficiency as follows:

$$CE_{\text{o}}^{{\prime \prime }} = \frac{{\sum_{\alpha = 1}^{q} {C_{o}^{\alpha } } }}{{\sum_{i = 1}^{m} {\sum_{{p \in P_{I} (i)}}^{{}} {\bar{x}_{io}^{p} } } }}.$$
(17)

\(CE_{o}^{\prime \prime }\) in (17) is the ratio of the aggregate minimum cost of processes \(\alpha ,\,\alpha = 1, \ldots ,q\), to the observed aggregate cost for multi-period network system.

On the other hand, we express the system global cost efficiency \(CE_{o}^{\prime \prime }\) as a weighted average of the global cost efficiencies of its processes as follows:

$$CE_{o}^{\prime \prime } = \sum\limits_{\alpha = 1}^{q} {w^{\alpha } } CE_{o}^{\alpha } ,\quad w^{\alpha } = \frac{{\sum_{i \in I(\alpha )}^{{}} {\bar{x}_{io}^{\alpha } } }}{{\sum_{i = 1}^{m} {\sum_{{p \in P_{I} (i)}}^{{}} {\bar{x}_{io}^{p} } } }},$$
(18)

where the weight \(w^{\alpha }\) is the relative importance of the total cost of inputs consumed by the process \(\alpha\) in T time periods to the total cost of all process (total cost of the system). This property can help decision makers identify the sources of inefficiency of a network system by recognizing the processes that are more effective in the cost inefficiency of the system.

Productivity change

The global cost Malmquist productivity index

In this section, we measure the productivity change of DMUo between two periods \(l\) and \(l + 1\) by the global cost Malmquist index (\(CM_{o}^{l,l + 1}\)). We define the index as follows:

$$CM_{o}^{l,l + 1} = \frac{{CE_{o}^{l} }}{{CE_{o}^{l + 1} }},$$
(19)

where \(CE_{o}^{l}\) was defined in (11) and \(CE_{o}^{l + 1}\) can be calculated similarly, after replacing \(l\) with \(l + 1\) in (11).

Clearly, deterioration in productivity between periods \(l\) and \(l + 1\) is occurred when \(CM_{o}^{l,l + 1} > 1\). An improvement in productivity between these periods is recognized when \(CM_{o}^{l,l + 1} < 1\), and productivity remains unchanged if \(CM_{o}^{l,l + 1} = 1\).

Theorem 2

For every DMUj, the index \(CM_{j}^{{}}\) has the circularity property.

Proof

$$CM_{j}^{l,l + 1} \times CM_{j}^{l + 1,l + 2} = \frac{{CE_{j}^{l} }}{{CE_{j}^{l + 1} }} \times \frac{{CE_{j}^{l + 1} }}{{CE_{j}^{l + 2} }} = \frac{{CE_{j}^{l} }}{{CE_{j}^{l + 2} }} = CM_{j}^{l,l + 2} .$$

□

Relationship between productivity changes of network system and its processes

Taking the productivity changes of the processes between two time periods \(l\) and \(l + 1\) into account, we define a productivity index again, \(PI_{o}^{l,l + 1}\), for DMUo as the ratio of the aggregate process global cost efficiency of period \(l\) to that of period \(l + 1\)

$$PI_{o}^{l,l + 1} = \frac{{\sum_{\alpha = 1}^{q} {CE_{o}^{\alpha l} } }}{{\sum_{\alpha = 1}^{q} {CE_{o}^{\alpha l + 1} } }},$$
(20)

where \(CE_{o}^{\alpha l} = {{C_{o}^{\alpha l} } \mathord{\left/ {\vphantom {{C_{o}^{\alpha l} } {\sum\nolimits_{i \in I(\alpha )} {\bar{x}_{io}^{\alpha l} } }}} \right. \kern-0pt} {\sum\nolimits_{i \in I(\alpha )} {\bar{x}_{io}^{\alpha l} } }}\) and \(CE_{o}^{\alpha l + 1} = {{C_{o}^{\alpha l + 1} } \mathord{\left/ {\vphantom {{C_{o}^{\alpha l + 1} } {\sum\nolimits_{i \in I(\alpha )} {\bar{x}_{io}^{\alpha l + 1} } }}} \right. \kern-0pt} {\sum\nolimits_{i \in I(\alpha )} {\bar{x}_{io}^{\alpha l + 1} } }},\) are the global cost efficiencies of the process \(\alpha\) in periods \(l\) and \(l + 1\), respectively. \(C_{o}^{\alpha l}\) is the minimum cost of producing a given final output vector \(y_{o}^{\alpha l} = (y_{1o}^{\alpha l} ,y_{2o}^{\alpha l} , \ldots ,y_{so}^{\alpha l} )\) and can be calculated by the following model,

$$\begin{aligned} C_{o}^{\alpha l} & = \hbox{min} \quad \sum\limits_{i \in I(p)}^{{}} {\bar{x}_{i}^{\alpha l} } \\ {\text{s}} . {\text{t}} .& \, \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{I} (i)}}^{{}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{pt} \bar{x}_{ij}^{pt} } } } \le \bar{x}_{i}^{\alpha l} ,\,\, \, \, \, i \in I(\alpha ), \\ & \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{O} (k)}}^{{}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{pt} y_{kj}^{pt} } } } \ge y_{ko}^{\alpha l} ,\,\,\, \, k = 1, \ldots ,s, \\ & \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{out} (r)}}^{{}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{pt} z_{rj}^{pt} } - } } \sum\limits_{t = 1}^{T} {\sum\limits_{{p \in P_{in} (r)}}^{{}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{pt} z_{rj}^{pt} } } } \ge 0, \, \quad r = 1, \ldots ,R, \\ & \lambda_{j}^{pt} \ge 0,\quad \quad \quad \, t = 1, \ldots ,T, \, j = 1, \ldots ,n,\,\,p = 1, \ldots ,q, \\ & \bar{x}_{i}^{\alpha l} \ge 0,\quad \quad \quad \quad \, i \in I(\alpha ).\quad \quad \\ \end{aligned}$$
(21)

\(C_{o}^{\alpha l + 1}\) also can be computed using model (21) after replacing time period \(l\) with \(l + 1\).

In the following, we will show that the productivity changes of network system can be defined as a weighted average of the process productivity changes if the weight for each process \(\alpha\) is considered as the ratio of the global cost efficiency of this process in period \(l + 1\) to the sum of those of all \(q\) processes. That is, we have

$$PI_{o}^{l,l + 1} = \sum\limits_{\alpha = 1}^{q} {w^{\alpha } CM_{\alpha o}^{l,l + 1} } ,\quad w^{\alpha } = \frac{{CE_{o}^{\alpha l + 1} }}{{\sum_{p = 1}^{q} {CE_{o}^{pl + 1} } }},\quad CM_{\alpha o}^{l,l + 1} = \frac{{CE_{o}^{\alpha l} }}{{CE_{o}^{\alpha l + 1} }}.$$
(22)

This relationship can be verified as follows:

$$\sum\limits_{\alpha = 1}^{q} {w^{\alpha } CM_{\alpha o}^{l,l + 1} } = \sum\limits_{\alpha = 1}^{q} {\left( {\frac{{CE_{o}^{\alpha l + 1} }}{{\sum_{p = 1}^{q} {CE_{o}^{pl + 1} } }}} \right)\left( {\frac{{CE_{o}^{\alpha l} }}{{CE_{o}^{\alpha l + 1} }}} \right)} = \sum\limits_{\alpha = 1}^{q} {\frac{{CE_{o}^{\alpha l} }}{{\sum_{p = 1}^{q} {CE_{o}^{pl + 1} } }}} = \frac{{\sum_{\alpha = 1}^{q} {CE_{o}^{\alpha l} } }}{{\sum_{p = 1}^{q} {CE_{o}^{pl + 1} } }} = \frac{{\sum_{\alpha = 1}^{q} {CE_{o}^{\alpha l} } }}{{\sum_{\alpha = 1}^{q} {CE_{o}^{\alpha l + 1} } }} = PI_{o}^{l,l + 1} .$$

Clearly, \(\sum_{\alpha = 1}^{q} {w^{\alpha } } = 1\) and \(w^{\alpha } \ge 0\). The weights \(w^{\alpha } ,\;\alpha = 1, \ldots ,q,\) reflect the importance of the productivity changes of process \(\alpha\) to the productivity changes of DMUo (network system) between two time periods. Our goal is to enter the relative importance of productivity change of each process into the productivity change of under evaluation DMU between two time periods. This can help decision makers identify the most effective processes in the productivity changes of network system.

Numerical example

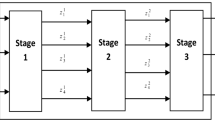
In this example, we consider 10 \({\text{DMUs}}\), each one has two stages, namely stage I and II, and observed in three time periods (10 multi-period network production systems). Each \({\text{DMU}}\) uses two exogenous inputs (\(x_{1}^{\text{It}}\) and \(x_{2}^{\text{It}}\)) to produce two intermediate products (\(z_{1}^{t}\) and \(z_{2}^{t}\) (and one final output (\(y_{1}^{\text{It}}\)) in stage I, and consumes two intermediate products generated in stage I and one exogenous input (\(x_{3}^{\text{IIt}}\)) to produce two final outputs (\(y_{2}^{\text{IIt}}\) and \(y_{3}^{\text{IIt}}\)) in stage II in time period \(t,\;t = 1,\,2,\,3\). Figure 1 depicts such situation.

Fig. 1
figure 1

Multi-period network production system (q = 2, T = 3)

Full size image

The data set of three time periods (t = 1, 2, and 3) is reported in Table 1. The cost vectors of periods 1, 2, and 3 are \((c_{1}^{1} ,c_{2}^{1} ,c_{3}^{1} ) = (2,1,2)\), \((c_{1}^{2} ,c_{2}^{2} ,c_{3}^{2} ) = (2,1,2)\), and \((c_{1}^{3} ,c_{2}^{3} ,c_{3}^{3} ) = (3,2,3)\), respectively.

Table 1 Data set for the time periods 1–3
Full size table

After solving model (6) for each DMU, we have the results shown in Table 2.

Table 2 The multi-period global cost efficiency of DMUs after 3 time periods
Full size table

We investigate the relationship between the global cost efficiencies of DMUs and their subsystems by model (9) and Eqs. (11) and (13). The results are shown in Table 3.

Table 3 Relationship between the global cost efficiency of DMUs and their subsystems
Full size table

We can see that the results in Tables 2 are almost similar to the results of Table 3. In fact, two approaches consider DMU I as the most efficient DMU among 10 DMUs.

Now, we compute the multi-period global cost efficiency of DMUs and their processes after 3 time periods and represent the relationship between them by model (15) and Eqs. (14), (17), and (18). The results are shown in Table 4.

Table 4 Relationship between the multi-period global cost efficiency of DMUs and their processes
Full size table

From the results of Table 4, it is clear that when we incorporate the efficiency of the processes in calculating the total efficiency, the same results are obtained. But using this approach we can examine the contribution of variations in individual processes in the evaluation of the global cost efficiency score of network system.

Now we compute the productivity changes of DMUs between time periods 1 and 2 and between time periods 2 and 3 using formulation (19). Table 5 shows the obtained results.

Table 5 Measuring productivity changes of DMUs using formulation (19)
Full size table

For instance, the greater than one values for \(CM_{A}^{1,2}\) and \(CM_{A}^{2,3}\) index indicate a regress in the productivity of DMU A between time periods 1 and 2 and also 2 and 3. The value of \(CM_{o}^{1,3}\) can be computed with due attention to the circularity property.

If we calculate the productivity change of DMUs by applying (21) and (22), we will have the results shown in Table 6.

Table 6 Measuring productivity changes of DMUs using the PI index
Full size table

By comparing the results of the two proposed approaches for calculating the productivity change of DMUs, we observe that the results obtained from the two approaches are almost similar for all DMUs. But the latter provides useful information about the contribution of productivity change of individual processes in the evaluation of the productivity change of network system between two time periods.

Conclusions

In this paper, we proposed a network DEA model to measure the multi-period global cost efficiency of networks when the prices of exogenous inputs are known, and defined the production possibility sets of individual periods, individual processes as well as the total network system. We showed that there is a relationship between the global cost efficiency of network system and its subsystems. In fact the operations of individual periods were taken into account in the evaluation of cost efficiency of the network system after T time periods. The main focus of this study was to incorporate the variations in individual processes in the evaluation of the global cost efficiency score of network system. We assumed that there is a relationship between the global cost efficiency of network system and its processes and used it to compute the network global cost efficiency after T periods of time.

The global cost Malmquist productivity index was computed to study the productivity changes of under evaluation network. This paper also presented another approach to examine the productivity change of DMUs over time that help decision makers recognize the most effective processes in the productivity changes of the network system between two time periods.

This paper can be extended to the case where the prices of the final outputs are at hand. In this case, a global profit Malmquist productivity index should be applied for measuring the productivity changes of the network system, and the most effective factors in this measurement may be identified to improve the productivity of the system. Another research topic is the case in which there are some final products that may be recognized as undesirable outputs.