1 Introduction

The synchrotron light source has been continuously evolved for higher brightness, and a recent multibend achromat lattice design enabled the synchrotron to offer a much lower horizontal emittance. This type of synchrotron is referred to as the 4th generation storage ring (4GSR). The 4GSR focuses on the hard X-ray regime (\(\sim\)0.1 nm) and can be considered as a diffraction-limited storage ring when the electron emittance is smaller than photon’s intrinsic emittance \(\lambda\)/4\(\pi\) (\(\lambda\), photon wavelength). Many advanced synchrotron light sources rushed into upgrading to the diffraction limited storage ring. MAX-IV is considered one of the successfully operating ones. In Korea, a new 4th generation storage ring (Korean 4GSR) will be constructed in Cheongju. Interestingly, this new synchrotron facility embraces industrial and multipurpose applications; even so, academic communities will also be the beneficiaries of these new light sources. The advances in the Korean 4GSR compared to the Pohang Light Source-II (PLS-II) lead to an almost two orders of magnitude increase in the coherent fraction and the brightness, as well as a smaller source size. These could impact the beamline’s design, such as its optics and experimental techniques.

In this paper, we briefly discuss the key factors for the storage ring and presents figures-of-merit for the undulator beamlines operated in the PLS-II, assuming they are in the upcoming Korean 4GSR. This should be helpful in understanding what can be expected from Korean 4GSR beamlines.

2 Key factors for storage ring

First of all, we discuss what determines the characteristics of a photon beam from the storage ring. The electron beam energy, emittance, and undulator length can be raised [1,2,3]. The electron beam energy determines the Lorentz factor \(\gamma\), which is given by

$$\begin{aligned} \gamma = \frac{E_{e}}{m_{e} c^{2}}, \end{aligned}$$
(1)

where \(\textit{m}\) \(_{e}\) is the rest mass of an electron and \({c}\) is the speed of light. The \(\gamma\) is directly related to the \({n}\)-th harmonic wavelength \(\lambda _{n}\) in the undulator spectrum on axis

$$\begin{aligned} \lambda _{n} = \frac{\lambda _{u}}{2 n \gamma ^{2}} \left( 1 + \frac{K^2}{2}\right) , \end{aligned}$$
(2)

with \(\lambda _{u}\) being the undulator magnet period and \({K}\) the deflection parameter, 0.934 \({\textit{B}_0 \lambda _u}\) (\({\textit{B}_0}\): maximum magnetic field). From Eqs. (1) and (2), the fundamental energy of the undulator is proportional to \({\textit{E}_{e}}^{2}\). For example, PLS-II’s \(\textit{E}\) \(_{e}\) is 3 GeV, and the \(\gamma\) is 5870. Then, the fundamental energy is about 2.8 keV for a 20-mm-period undulator (\({K}\) = 1). When \(\textit{E}\) \(_{e}\) increases to 4 GeV or 6 GeV, the fundamental energy shifts to 5.1 keV or 11.5 keV, respectively.

For 3rd generation storage rings such as PLS-II, the emittance (\(\epsilon\)) is on the order of nm\(\cdot\)rad. The 4th generation storage ring is designed to lower the emittance, especially the horizontal emittance (\(\epsilon _{\mathrm{H}}\)) by as much as the order of pm\(\cdot\)rad. The emittance is a constant value for a storage ring. The vertical emittance (\(\epsilon _{\mathrm{V}}\)) is coupled with the horizontal emittance (\(\epsilon _{\mathrm{H}}\)) via the coupling constant, \(\kappa\). \(\kappa\) is about 1\(\%\) for 3rd generation storage rings and 10\(\%\) for 4th generation storage rings. In the hard X-ray regime, a small coupling constant (\(\sim\)1\(\%\)) is needed for 3rd generation storage rings if the vertical electron emittance is to approach diffraction-limited value compared to the large horizontal emittance. However, in the 4th generation storage ring, the horizontal electron emittance due to multibend-achromat is significantly reduced to the diffraction-limited value, so even a coupling constant of about 10\(\%\) is sufficient to maintain the vertical electron emittance with the diffraction-limited value [3]. With this value for \(\epsilon\), one can tune the beam size (\(\sigma\)) and beam divergence (\(\sigma ^{\prime }\)) by using the beta function, \(\beta\):

$$\begin{aligned} \sigma _{H,V}= & {} \sqrt{\epsilon _{H,V} \beta _{H,V}}, \end{aligned}$$
(3a)
$$\begin{aligned} \sigma _{H,V} ^{\prime }= & {} \sqrt{\epsilon _{H,V}/{\beta _{H,V}}}. \end{aligned}$$
(3b)

For the undulator, the brightness, B, and coherent flux, \(F_c\), are

$$\begin{aligned} B= & {} \frac{F}{4\pi ^2 \epsilon _H \epsilon _V}, \end{aligned}$$
(4a)
$$\begin{aligned} F_c= & {} B\Big (\frac{\lambda }{2}\Big )^2. \end{aligned}$$
(4b)

where F is the total spectral photon flux, number of photons/s/0.1%BW. The fact that the 4th generation storage ring has a 100 times smaller emittance than the 3rd generation one implies that the B and the \(F_c\) of the 4GSR increase by 100 times.

The last characteristic factor is the undulator length (\({L}\)). The photon beam size (\(\sigma _{r}\)) and the divergence (\(\sigma _{r}^{\prime }\)) generated by the undulator are functions of the \({L}\), assuming single electron radiation :

$$\begin{aligned} \sigma _{r}= & {} \frac{\sqrt{2\lambda L}}{2\pi }, \end{aligned}$$
(5a)
$$\begin{aligned} \sigma _{r}^{\prime }= & {} \sqrt{\frac{\lambda }{2L}}. \end{aligned}$$
(5b)

When \({L}\) increases from 1 m to 4 m, the \(\sigma _{r}\) increases by a factor of 2 and \(\sigma _{r}^{\prime }\) decreases by a factor of 1/2. For the 4GSR, the electron beam divergence and photon beam divergence are compatible with each other. Hence, a longer undulator has a smaller convoluted photon beam divergence. The triad of the above-mentioned set of parameters-electron beam energy, emittance, and undulator length-will become key factors in determining all the benefits from the 4GSR, such as the flux density at the sample stage, the efficiency in the instrumentations, especially the spectrometer to resolve the X-ray beam scattered from the sample, and even a new conceptual development for both beam-control and an experimental scheme.

Table 1 Korean 4GSR and PLS-II parameters [4, 5]
Full size table

3 Korean 4GSR and PLS-II

3.1 Storage ring and undulator

We discuss the fundamental differences between the Korean 4GSR and the PLS-II. Table 1 shows the currently suggested Korean 4GSR’s and PLS-II’s storage ring parameters. The Korean 4GSR is considered to be a diffraction-limited storage ring on the hard X-ray regime, and its emittance is 58 pm \(\cdot\)  rad, which is 100 times smaller than PLS-II’s. The electron energy of the Korean 4GSR is chosen to be 4 GeV, which shifts the photon energy range to higher value compared to the PLS-II’s. The critical energy of the Korean 4GSR is 21.3 keV for the bending magnet [4]. The energy of the fundamental radiation from a 20-mm period undulator moves to 5.1 keV (4 GeV) from 2.8 keV (3 GeV). Depending on the undulator period, a higher electron beam energy allows the fundamental harmonics to shift to much higher energy.

Fig. 1
figure 1

Phase space of a, b PLS-II (L = 1.4 m), c, d Korean 4GSR (L = 1.4 m), and e, f Korean 4GSR (L = 5 m) (\(\lambda\) = 0.1 nm, black: electron beam, blue: photon beam, red: convoluted, insets: enlarged plots at the center)

Full size image
Fig. 2
figure 2

a Calculated spectra of 1C IVU (\(\lambda _u\) = 20 mm) at a 6-mm gap for the PLS-II (black) and the Korean 4GSR (blue) (red: \({L}\) = 5 m) and b the spectral flux density plot of a

Full size image

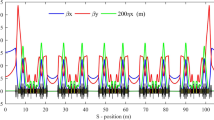
The sizes and the divergences of the electron beam source are calculated from SPECTRA [6]. The size and the divergence of the photon source are calculated by using the measured gap-magnetic field table from the 1.4-m hard X-ray in-vacuum undulator, which is installed in the PLS-II 1C beamline. Figure 1 shows the calculated results at \(\lambda\) = 0.1 nm. The black ellipse in Fig. 1a is PLS-II’s horizontal source size (\(\sigma _{\mathrm{H}}\)) and divergence (\(\sigma _{\mathrm{H}}^{\prime }\)) of the electron beam, 187 \(\upmu\)m (r.m.s.) and 47 \(\upmu\)rad (r.m.s), respectively. The blue ellipse is the \(\sigma _{\mathrm{H}}\) and the \(\sigma _{\mathrm{H}}^{\prime }\) of the photon beam from the undulator, about 6.0 \(\upmu\)m (r.m.s) and 2.7 \(\upmu\)rad (r.m.s). The electron beam’s \(\sigma _{\mathrm{H}}\) and \(\sigma _{\mathrm{H}}^{\prime }\) are more than one order of magnitude higher so that the electron beam mostly determines the convoluted photon beam’s (red ellipse). The \(\sigma _{\mathrm{V}}\) and \(\sigma _{\mathrm{V}}^{\prime }\) of the electron and the photon beams are comparable to each other, but still the \(\sigma _{\mathrm{V}} ^{\prime }\) of the electron beam is larger than that of the photon beam. However, the Korean 4GSR gives much smaller electron \(\sigma _{\mathrm{H}}\) and \(\sigma _{\mathrm{H}} ^{\prime }\), as shown in Fig. 1c. The electron and the photon beam’s \(\sigma\) and \(\sigma ^{\prime }\) of the Korean 4GSR are comparable to each other (Fig. 1c, d). The convoluted photon’s source sizes and divergences are \(\sigma _{\mathrm{H}}\) = 21 \(\upmu\)m (r.m.s), \(\sigma _{\mathrm{H}} ^{\prime }\)= 6.5 \(\upmu\)rad (r.m.s), \(\sigma _{\mathrm{V}}\) = 6.1 \(\upmu\)m (r.m.s), and \(\sigma _{\mathrm{V}} ^{\prime }\)= 4.9 \(\upmu\)rad (r.m.s), and the convoluted \(\sigma\) and \(\sigma ^{\prime }\) can be changed by choosing an appropriate \({L}\). For example, Fig. 1e, f display the convoluted \(\sigma\) and \(\sigma ^{\prime }\) for the case of \({L}\) equal to 5 m.

Fig. 3
figure 3

Spatial distribution (1st harmonic) of the photon beam at the source point of the a PLS-II and the b Korean 4GSR, and full width at half maximum (FWHM) of 0.1-nm X-ray beam sizes (c \(\Sigma _{\mathrm{H}}\) horizontal and d \(\Sigma _{\mathrm{V}}\) vertical) as a function of the distance from 1C IVU (black: PLS-II, red: Korean 4GSR)

Full size image
Fig. 4
figure 4

2D power density at 22 m from the source of a the PLS-II 1-m IVU, b the PLS-II 5-m IVU, and c the Korean 4GSR 5-m IVU (6 mm gap, \({K}\)=1.58). d Horizontal and e vertical power density profiles of a–c (black: PLS-II 1-m IVU, blue: PLS-II 5-m IVU, red: Korean 4GSR 5-m IVU). f X-ray footprint (S\(_{P}\)) on the first crystal of the DCM at 22-m as a function of X-ray energy (\(\theta _{B}\): Bragg angle, assuming a beam size of 1 mm in vertical direction). Peak power thresholds are annotated as (1) PLS-II 5 m (> 8 keV) and (2) Korean 4GSR 5 m (> 26 keV)

Full size image

Due to its smaller emittance, the Korean 4GSR gives higher brightness because the brightness is inversely proportional to the emittance. We calculated the spectra of the 1C in-vacuum undulator (IVU, \(\lambda _u\) = 20 mm period and \({L}\) = 1.4 m) for the Korean 4GSR and the PLS-II at an observation point of 36 m from the source. The slit sizes for the calculation were set as 0.68 (V)  \(\times\)  4.0 (H) mm\(^{2}\) and 0.53 (V)  \(\times\)  0.55 (H) mm\(^{2}\), which are the beam sizes at 36 m for the PLS-II and the Korean 4GSR. Figure 2a shows the spectral flux for the given beam sizes. Below 15 keV, the flux increases by less than 3 times, but above 25 keV it increases by more than one order of magnitude. Obviously, this is a clear advantage in high-energy X-ray applications. The 4 GeV of the Korean 4GSR shifts the fundamental harmonic of the 1C IVU from 1.9 to 3.4 keV when its gap is 6 mm. If we consider the flux density, the spectral flux density of 1C IVU of the Korean 4GSR (blue) is higher by about one order of magnitude up to 15 keV and by two orders of magnitude above 25 keV. If more total flux is to be achieved, a longer undulator should be inserted. The red spectrum in Fig. 2 is the calculated result for \({L}\) = 5 m. Roughly two (< 15 keV) and three (> 25 keV) orders of magnitude increases are seen in the spectral flux density. Of note is that the spectral flux at higher harmonics in a real undulator decreases more than it does for the ideal source because the undulator requires perfect alignment and precise tuning to reduce phase jitter between the electron and the photon paths. Higher harmonics are more sensitive to these errors [7].

3.2 Beamline optics

The X-ray beam’s size at a distance from the source is calculated from the source size and divergence, and the results are plotted in Fig. 3. The beam sizes at the source points of the Korean 4GSR and the PLS-II show a clear difference in the horizontal direction (Fig. 3a, b). The full width at half maxima (FWHM) for the source sizes of the PLS-II and the Korean 4GSR are 440 \(\upmu\)m (H)  \(\times\)  31 \(\upmu\)m (V) and 50 \(\upmu\)m (H)  \(\times\)  12 \(\upmu\)m (V), respectively. The horizontal X-ray beam size at 36 m is dramatically decreased from 4.0 mm (PLS-II) to 0.6 mm (Korean 4GSR), but the vertical ones are similar, (0.7 mm for the PLS-II and 0.5 mm for the Korean 4GSR) mostly due to the improved \(\epsilon _{\mathrm{H}}\).

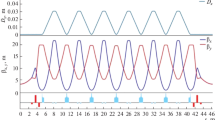
The first optics in the beamline deal with the heat load from the undulator. Figure 4a–c show the 2D power density at 22 m (gap = 6 mm, \({K}\)=1.58) for the 1-m and 5-m IVU of the PLS-II, and the 5-m IVU of the Korean 4GSR. Generally, the first crystal of the double crystal monochromator (DCM) with the liquid nitrogen cooling manages the heat load. The designed cooling powers of the DCM in the PLS-II have a maximum power of \(\sim\)500 W and a maximum power density of \(\sim\)35 W/mm\(^{2}\). Figure 4d, e show the power density profiles at 22 m for each source. The power densities for the 5-m IVU in the PLS-II and the Korean 4GSR are 5 and 17 times higher than that for the 1-m IVU in the PLS-II, respectively. At the first crystal of the DCM, the power density is naturally reduced by a factor of the X-ray beam’s footprint, S\(_{P}\) (Fig. 4f). When the vertical beam size is 1 mm, the footprints on the first Si crystal are shown in Fig.  4f as a function of the X-ray energy. The increasing footprint on the first crystal means the power density on the surface is reduced by S\(_{P}\). From the footprint on the first crystal, we can estimate the peak power threshold at the DCM’s position (22 m) in the PLS-II, and the heat load can barely be managed only when the DCM energy set values are above 8 keV and 26 keV for the 5-m IVU in the PLS-II and the Korean 4GSR. However, this huge heat load can be reduced in several ways. The primary slit defining the central cone of the undulator harmonics reduces the total power, and low energy filters, such as diamond or beryllium windows, block the low-energy part of the full energy spectrum. For a large circumference storage ring, the high power density is mitigated by locating the first optics further from the source, such as at 40 m, which effectively decreases the power density on the optics.

Fig. 5
figure 5

Si(111) single-crystal Darwin width (black \(\circ\): Si(111), blue \(\circ\): Si(113), and red \(\circ\): Si(333)), and vertical X-ray beam divergences (FWHM, black curve: PLS-II 1C IVU, blue curve: Korean 4GSR 1C IVU, and red curve: Korean 4GSR 1C IVU (5 m))

Full size image

Single crystal Si(111) is a commonly used monochromator crystal, and the relative energy resolution of a Si(111) DCM is \(\sim\)1.3 \(\times\) 10\(^{-4}\). Figure 5 shows the reason it has been used. When the incident X-ray beam has a smaller vertical divergence than the Si(111) Darwin width, i.e., the total reflection region, the monochromatic beam within its bandwidth is reflected without loss. The X-ray beam from the 1C IVC in the PLS-II has a divergence of less than 23 \(\upmu\)rad. It is smaller than single Si(111) crystal’s Darwin width up to 15 keV. The DCM can transport the monochromatic beam without flux loss up to 15 keV. However, when a Si(113) crystal is used for higher relative energy resolution (\(\sim\)3.5 \(\times\) 10\(^{-5}\)), its Darwin width becomes smaller than the PLS-II’s divergence, above 6.5 keV and the Korean 4GSR’s above 8 keV. In this case, some of the incident flux is lost. As seen in Fig. 5, the 5-m-long IVU of the Korean 4GSR produces an X-ray beam with a divergence smaller than the Darwin width of the Si(111) single crystal up to 40 keV. In other words, a beamline with a Si(111) monochromator in the Korean 4GSR with a 5-m IVU can provide a monochromatic X-ray beam without flux loss, which is an additional advantage. Also, no flux is lost with a Si(113) monochromator in the X-ray energy range (< 17 keV) where most of transition metal elements’ absorption edges are. This gives a higher energy resolution and a higher flux for the spectroscopy applications.

3.3 Resonant inelastic X-ray scattering

Resonant inelastic X-ray scattering (RIXS) is one of the most powerful experimental techniques to probe both the electronic and the crystallographic structures of matter. Because RIXS is a second-order photon-in photon-out process with a very low X-ray emission efficiency, it is a notoriously photon-hungry experimental technique even in modern storage ring facilities. However, during the last decades, outstanding progress has been made both in the beamline optics, including spectrometer and especially detector technology, thus enabling us to dive into this harsh research area. Most interesting elementary excitations observed in condensed matter systems, such as phonons, magnons, d–d excitations, orbitons, charge transfer gaps, interband transitions, and even plasmons have been successfully studied through RIXS experiments [8, 9]. Because of the versatility of RIXS, materials under investigation cover most of the major fields of current X-ray science, for example quantum-, energy-, and bio-specimens.

A key issue in RIXS is an appropriate energy resolution for probing a particular excitation mode in a specific material system. More delicate monochromators, focusing optics, spectrometers, and position sensitive detectors are used to deal with proper energy resolution from several tens of meV to hundreds of meV in 3rd generation synchrotron radiation beamlines. However, the mismatch between the properties of the source from the storage ring and the characteristics of perfect crystal optics causes an inefficient utilization of an X-ray beam source, which results in an overall degradation in the intensity and the energy resolution of beamline instruments. In this section, we clarify the benefit of RIXS performance from the enhanced source properties in the Korean 4GSR under comparison with these of the RIXS testing facility at the 3A beamline in the PLS-II.

Fig. 6
figure 6

a RIXS spectrum of a Sr\(_2\)IrO\(_4\) single crystal near the Ir L\(_3\)-edge. The white rectangle in the top left-hand corner of the figure indicates the spectral bandwidth of incident X-rays (\(\Delta E_i\) = 0.31 eV) in the vertical direction and scattered X-rays (\(\Delta E_s\) = 0.32 eV) in horizontal direction. b Incident X-ray spectrum (\(\Delta E_i\) = 0.31 eV)

Full size image

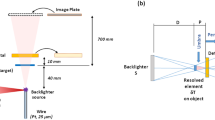
We performed RIXS experiments for a Sr\(_2\)IrO\(_4\) single crystal with the (001) surface normal near the Ir L\(_3\)-edge (11.215 keV) at the 3A beamline of the PLS-II. The scattered signal perpendicular to the sigma polarized incident beam (2\(\theta\) = 90\(^{\circ }\), \(\sim\) Q = (0, 0, 33) forbidden reflection) in the horizontal scattering plane was analyzed because the elastic scattering intensity becomes weak due to the polarization factor of Thomson scattering. The RIXS plane of the energy loss and the incident energy in Fig. 6a clearly shows an optically forbidden d–d excitation peak at 0.6-eV energy loss (the red dashed line) due to the d-state splitting from the spin-orbit coupling, which is consistent with the result in a previous report [10]. In order to resolve this energy loss from the elastic line and maintain a reasonable X-ray intensity for the data acquisition time, we used a Si(333) DCM and adjusted the primary slits to control the X-ray beam’s divergence. The incident X-ray energy resolution is determined by using both the intrinsic Darwin width of the crystal reflection and the angular divergence of the incoming X-ray beam. In Fig. 6b, the spectral bandwidth, 0.31 eV, of the incident X-ray at 11.215 keV was measured from the strong elastically scattered signal from several sheets of Scotch Magic tape. Compared with the intrinsic Darwin width (\(\sim\) 0.10 eV) of the Si(333) reflection at Ir L\(_3\)-edge, the measured value of 0.31 eV was very large, indicating that the angular divergence dominated the overall energy resolution of the incident X-ray beam. Using both the measured energy resolution and the Darwin width, we could estimate the angular divergence as about 20 \(\upmu\)rad, which agrees with the calculated value for the 3A undulator source. The incident X-ray energy resolution, 0.31 eV, is enough to resolve the d–d excitation spectrum of our sample, so we performed the experiment without reducing the angular divergence contribution to energy resolution of the incident X-ray. The RIXS intensity was accumulated for 60 s to improve the signal (\(\sim\)2–4 cps)-to-noise ratio.

RIXS spectrometers mainly consist of a spherical diced crystal analyzer (SDCA) and a one-dimensional micro-strip detector on the Rowland circle geometry. The energy resolution of the spectrometer is determined by the diced crystal Darwin width, the strip-detector pitch, and the beam size. The energy resolution of the spectrometer depends on the spatial resolution of the detector, which can be discriminated according to its position as an energy parameter [11]. Recent advances in detector technology using micro-strips greatly enhanced the energy resolution of the scattered beam by up to several tens of times [12]. The pitch of the micro-strip detector was 50 \(\upmu\)m, corresponding to a detector spectral bandwidth of 0.02 eV at 11.215 keV. The beam size in the vertical direction at the sample position was set to about 60 \(\upmu\)m by the focusing the mirror system. The calculated spectrometer energy resolution is about 0.079 eV, which is much smaller than the incident X-ray energy resolution. Hence, the total experimental energy resolution of 0.32 eV is dominated by the incident X-ray resolution. For higher RIXS energy resolution (< 0.10 eV), a secondary high-resolution channel-cut monochromator setup is required, but that would reduce the incident X-ray intensity significantly in the PLS-II.

When the RIXS test facility of the 3A beamline is assumed in the Korean 4GSR, the photon source has a much smaller beam divergence and size. This enhances the beamline optics’ capabilities in terms of achievable energy resolution and signal intensity. Therefore, the above-mentioned flux issue in the PLS-II can be resolved to a considerable degree. Furthermore, opportunities for new designs of the RIXS spectrometer are expected. For example, the imaging-\(h\nu ^2\) spectrometer in soft X-ray regime, which can measure the RIXS plane in one shot, has been proposed and realized [13, 14]. This cannot be directly applied to the hard X-ray RIXS spectrometer, but the 4GSR has much room for new concepts to be developed.

Fig. 7
figure 7

Au L\(_{\alpha }\) RXES map and line profiles (XAS, HERFD, HEROS) for a Au(CN)\(_{2}\) 0.25-M aqueous solution

Full size image
Table 2 Expected gain factors from the Korean 4GSR compared with these for the 1.4-m IVU in the PLS-II
Full size table

3.4 Resonant X-ray emission spectroscopy

When X-ray photons are absorbed in a particular system, core holes are created. The upper level electron refills the core hole, and it emits a photon. In spite of the low yield, resonant X-ray emission spectroscopy (RXES) gives information on the occupied states of the system whereas X-ray absorption spectroscopy probes the unoccupied states. We used RXES to obtain Au L\(_\alpha\) data from a 0.25-M Au(CN)\(_3\) aqueous solution at the 1C beamline. The incident X-ray was tuned to the Au L\(_{3}\) edge (11.919 keV), and its intensity was \(\sim\)10\(^{11}\) photons/s. The X-ray was focused at a sample position of 40 \(\upmu\)m (V)  \(\times\)  400 \(\upmu\)m (H) by using a toroidal mirror. The X-ray emission spectrometer with a horizontal von-Hamos geometry and cylindrically focused Si(008) crystal analyzer (curvature 250 mm, length 200 mm, width 25 mm) was used [15]. The strip detector was exposed for 60 s to increase the data’s quality. The Au L\(_{\alpha 1}\) emission line width is 8.66 eV (Fig. 7 upper panel), which is mostly dominated by the natural broadening, 5.54 eV, and the horizontal beam size contribution, 5.66 eV [16]. The maximum peak intensity is around 15 cps in the RXES map (Fig. 7 center).

In additional to the resonant X-ray emission, other promising techniques, such as high-energy resolution fluorescence detection (HERFD) and high-energy resolution off-resonance spectroscopy (HEROS) [17], which are presented by the vertical red dotted line crossing the resonant point and the horizontal line below 10 eV from the absorption edge, respectively, in Fig. 7 can be used. The HERFD 2-eV resolution data is plotted with the total fluorescence X-ray absorption spectroscopy (XAS) data in the right panel. The bottom panel shows the HEROS data, which in principle directly correspond to high resolution X-ray absorption spectrum and was measured without scanning the incident X-ray energy; it can avoid the self-absorption effect [17].

For the comparison, we assume that the same spectrometer is installed in the Korean 4GSR. The X-ray total flux at 11.92 keV increases by 3.4 and 16.2 times for 1.4-m and 5-m IVUs. The vertical divergences of the X-ray beam from the undulators in the PLS-II and the Korean 4GSR are smaller than the Darwin width of Si(111) below 15 keV so that There is no loss and no gain. Also, the designed mirror can accept the full beam size in either case. Hence, the total flux gains at the sample position from the PLS-II to the 4GSR are transferred from the sources. Clearly, 5-m-long undulator can improve the total flux by more than one order of magnitude.

What is missing in this argument is the beam size. As shown in Fig. 2b, the beam size effect can be converted into flux density gains, which are 32 and 150 times for the 1.4-m and 5-m IVUs. The beam size at the sample position of the Korean 4GSR should be less than 5 \(\upmu\)m (V)  \(\times\)  20 \(\upmu\)m (H), which was estimated using the source size and a demagnification factor \(\sim\)3 for the toroidal mirror. The horizontal beam size affects the spectrometer’s resolution, which is a convolution of the beam size at the sample, the detector pixel’s size, and the analyzer’s crystal Darwin width. Among them, the energy resolution contributed by the beam size is tremendously reduced from 5.66 eV (400 \(\upmu\)m) to 0.28 eV (20 \(\upmu\)m) due to the Korean 4GSR’s small beam size. The RXES data for the intensity of the Korean 4GSR can be improved by 480 or 2250 times in order to obtain the same resolution of 0.28 eV due to the beam size, as summarized in Table 2. Further improvement in the RXES data intensity (quality) of Korean 4GSR can be made by focusing a much smaller beam size.

4 Conclusions and perspectives

We presented a comparative study of the hard X-ray undulator beamline in the PLS-II for the Korean 4GSR, based on the assumption of “what if the hard X-ray undulator beamline in PLS-II \(\textit{as it is}\) conceptually moves to the Korean 4GSR”. The hard X-ray undulator in the Korean 4GSR gives about three times (< 15 keV) and more than 1 order of magnitude higher total flux (> 25 keV) than the PLS-II. However, that the spectral brightness (flux density) of the Korean 4GSR is orders of magnitude higher than that of the PLS-II mainly due to the much smaller emittance should be emphasized. The Korean 4GSR’s smaller beam size gives practical advantages for various experiments [18] and offers greater opportunities for the high-energy applications (> 30 keV) [19].

Here, we lay out some of the challenges to and the opportunities for the Korean 4GSR. First is a newly developed undulator design. The round-shaped, small-sized, electron-beam characteristics of the 4GSR is one of the most important property distinguishing it from other previous storage rings. Very compact, isotropic, i.e., no bias in design such as horizontal or vertical ones, a new undulator source can be installed. One of the interesting possibilities is the choice of a superconducting, double-helical, compact undulator for versatile polarization control of the X-ray source. The horizon of the spectroscopic probe of the electronic structure of matter by using synchrotron radiation can be dramatically extended by freely controlling the incoming X-ray’s polarization states. Linear horizontal, linear vertical, circular right-handed, circular left-handed, and even X-ray beam states carrying orbital angular momentum can be controlled both statically and dynamically, which is limited by the maximum current ramping rate of the superconducting coils [20]. In addition to controlling the photon’s polarization states, other factors such as a much higher brightness are needed. Several types of undulators (revolver-type undulator, cryogenic permanent-magnet undulator and superconducting undulator) can meet some of the requirements so that the undulator design has to be carefully considered for each application.

The second is smaller beam size. As the source size of the Korean 4GSR becomes smaller, 50 \(\upmu\)m (H)  \(\times\)  12 \(\upmu\)m (V), a several micron-sized beam can relatively easily be achieved by using conventional mirrors or compound refractive lenses without compromising their angular acceptance. The demagnification factor of the focusing optics itself translates into a flux density gain, which increases the signal intensity from the sample. For RIXS and RXES, a smaller beam size contributes to better overall energy resolution. Furthermore, a submicron-sized beam can be achieved by using a Kirkpatrick–Baez (KB) mirror, which results in more than two orders of magnitude flux density improvement at the sample position. A micron- or a submicron-sized beam has a great impact on high pressure science [19] and protein crystallography. However, such small beams require mechanical stability of the optics and instrumentation, which would be an engineering challenge.

Lastly, we would like to briefly mention the increased coherence flux and machine learning for synchrotron applications. The 4GSR’s two orders of magnitude improvement in the coherent flux directly affects the coherent diffraction imaging (CDI) and X-ray photon correlation spectroscopy (XPCS) [21,22,23]. For example, in the case of CDI, the conventional imaging technique can be extended to include an extra dimension, such as the X-ray energy or the time delay in pump-probe experiments. The XPCS also can have an extended probing region of phase space, thus enabling systematic studies of the collective modes of spin, lattice, and charge degrees of freedom in many condensed matter systems. After innovative advances in deep supervised learning, machine learning (ML) has been perceived as one of the major disruptive technologies in the 21th century for recognizing patterns in big data [24]. The synchrotrons’ accelerator parts have already approached the ML method to stabilize source size [25]. Given the fact that synchrotrons have encountered the issue of big data [26], the beamline parts also need to consider machine learning, especially in data collection, data reduction, and data analysis, for better optimization of the beamline or even discovering patterns hidden in the experimental data, which would be too much to handle otherwise.