Skip to main content
SpringerLink
Log in

Empirical Approach for Determining Axial Strength of Circular Concrete Filled Steel Tubular Columns

  • Original Contribution
  • Published:
Journal of The Institution of Engineers (India): Series A Aims and scope Submit manuscript

Abstract

The concrete filled steel tubular (CFST) columns are highly regarded in recent years as an interesting option in the construction field by designers and structural engineers, due to their exquisite structural performance, with enhanced load bearing capacity and energy absorption capacity. This study presents a new approach to simulate the capacity of circular CFST columns under axial loading condition, using a large database of experimental results by applying artificial neural network (ANN). A well trained network is established and is used to simulate the axial capacity of CFST columns. The validation and testing of the ANN is carried out. The current study is focused on proposing a simplified equation that can predict the ultimate strength of the axially loaded columns with high level of accuracy. The predicted results are compared with five existing analytical models which estimate the strength of the CFST column. The ANN-based equation has good prediction with experimental data, when compared with the analytical models.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Abbreviations

Ac :

Area of the concrete section

Ay :

Area of the steel section

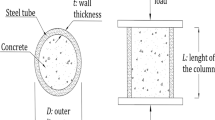
D:

Diameter of circular cross-section

t:

The thickness of the steel tube

fy :

Yield strength of the steel tube

Ea :

Modulus of elasticity of steel

fck :

The characteristic concrete strength

Ec :

The secant modulus of elasticity of concrete

L:

The length of the column

fconf :

Confined compressive strength of concrete

ηc :

The coefficient of confinement of concrete

fcp :

Unconfined compressive strength of concrete

ϒc :

Strength reduction factor introduced to the scale effect into consideration

\({\text{f}}_{\text{c}}^{{\prime }}\) :

The unconfined cylinder compressive strength of concrete

Dc :

Diameter of the core

References

  1. ACI (American Concrete Institute), Committee ACI 318-1995: Building Code Requirements for Structural Concrete (Farmington Hills, Michigan, 1995)

    Google Scholar 

  2. M. Ahmadi, H. Naderpour, A. Kheyroddin, Utilization of artificial neural networks to prediction of the capacity of CCFT short columns subject to short term axial load. Arch. Civ. Mech. Eng. 14, 510–517 (2014)

    Article  Google Scholar 

  3. AS (Australian Standards), AS 4100: Steel Structures (Standards Australia, Sydney, 1998)

    Google Scholar 

  4. A.T.A. Dantas, M.B. Leite, K. de Jesus Nagahama, Prediction of compressive strength of concrete containing construction and demolition waste using artificial neural networks. Constr. Build. Mater. 38, 717–722 (2013)

    Article  Google Scholar 

  5. B. Dutta, S.K. Bhattacharyya, An experimental study on the behaviour of concrete filled light gauge steel tubular columns. Indian Concrete J. 10, 477–480 (1995)

    Google Scholar 

  6. EC (Eurocode), EC-4: Design of Composite Steel and Concrete Structures—General Rules and Rules for Buildings (British Standard Institutions, London, 2004)

    Google Scholar 

  7. E. Ellobody, B. Young, Behaviour of normal and high strength concrete-filled compact steel tube circular stub columns. J. Constr. Steel Res. 62, 706–715 (2006)

    Article  Google Scholar 

  8. A. Elremaily, A. Azizinamini, Behavior and strength of circular concrete-filled tube columns. J. Constr. Steel Res. 58, 1567–1591 (2002)

    Article  Google Scholar 

  9. A. Fam, F.S. Qie, S. Rizkalia, Concrete filled tubes subjected to axial compression and under cyclic loads. J. Struct. Eng. 130, 631–639 (2004)

    Article  Google Scholar 

  10. G.D. Garson, Interpreting neural-network connection weights. AI Expert 6, 47–51 (1991)

    Google Scholar 

  11. G. Giakoumelis, D. Lam, Axial capacity of circular concrete-filled tube columns. J. Constr. Steel Res. 60, 1049–1068 (2004)

    Article  Google Scholar 

  12. C.D. Goode, ASCCS Database of Concrete-Filled Steel Tube Columns. http://web.ukonline.co.uk/asccs2/. Accessed 12 Feb 2013

  13. P.K. Gupta, S.M. Sarda, M.S. Kumar, Experimental and computational study of concrete filled steel tubular columns under axial loads. J. Constr. Steel Res. 63, 182–193 (2007)

    Article  Google Scholar 

  14. L.-H. Han, J.-S. Huo, Y.-C. Wang, Behavior of steel beam to concrete-filled steel tubular column connections after exposure to fire. J. Struct. Eng. 10, 800–814 (2007)

    Article  Google Scholar 

  15. L.-H. Han, W. Li, R. Bjorhovde, Developments and advanced applications of concrete-filled steel tubular (CFST) structures: members. J. Constr. Steel Res. 100, 211–228 (2014)

    Article  Google Scholar 

  16. G.D. Hatzigeorgiou, Numerical model for the behavior and capacity of circular CFT columns. Part II: verification and extension. Eng. Struct. 30, 1579–1589 (2008)

    Article  Google Scholar 

  17. H.J. Helena, M. Neelamegam, G.M. Samuel Knight, Investigation on the behaviour of concrete filled columns. J. Struct. Eng. 34, 257–265 (2007)

    Google Scholar 

  18. S.K. Jain, P.C. Nayak, K.P. Sudheer, Models for estimating evapotranspiration using artificial neural networks, and their physical interpretation. Hydrol. Process. 22, 2225–2234 (2008)

    Article  Google Scholar 

  19. S. Lai, M. Serra, Concrete strength prediction by means of neural network. Constr. Build. Mater. 11, 93–98 (1997)

    Article  Google Scholar 

  20. S.-H. Lee, B. Uy, S.-H. Kim, Y.-H. Choi, S.-M. Choi, Behavior high strength of circular concrete-filled steel tubular (CFST) Columns under eccentric loading. J. Constr. Steel Res. 67, 1–13 (2011)

    Article  Google Scholar 

  21. C.K. Leung, M.Y. Ng, H.C. Luk, Empirical approach for determining ultimate FRP strain in FRP-strengthened concrete beams. J. Compos. Constr. 10, 125–138 (2006)

    Article  Google Scholar 

  22. Z.H. Lu, Y.G. Zhao, Mechanical behavior and ultimate strength of circular CFT columns subjected to axial compression loads, in 14th World Conference on Earthquake Engineering, Beijing (2008)

  23. J.B. Mander, M.J.N. Priestley, R. Park, Theoretical stress–strain model for con fined concrete. J. Struct. Eng. 114, 1804–1826 (1988)

    Article  Google Scholar 

  24. E.K. Mohanraj, S. Kandasamy, Experimental behaviour of axially loaded hollow steel columns in-filled with concrete. IE(I) J.-CV 88, 23–29 (2008)

    Google Scholar 

  25. E.K. Mohanraj, S. Kandasamy, N. Rajkumar, Study on concrete using waste materials by partial replacement of aggregates to reduce global warming gases. Indian J. Sci. Technol. 3, 159–163 (2011)

    Google Scholar 

  26. S. Morino, K. Tsuda, Design and construction of concrete-filled steel tube column system in Japan. Earthq. Eng. Eng. Seismol. 4, 52–72 (2003)

    Google Scholar 

  27. A. Oztas, M. Pala, E. Ozbay, E. Kanca, N. Caglar, M. Asghar Bhatti, Predicting the compressive strength and slump of high strength concrete using neural network. Constr. Build. Mater. 20, 769–775 (2006)

    Article  Google Scholar 

  28. M. Pala, E. Ozbay, A. Oztas, M.I. Yuce, Appraisal of long-term effects of fly ash and silica fume on compressive strength of concrete by neural networks. Constr. Build. Mater. 21, 384–394 (2007)

    Article  Google Scholar 

  29. V.P. Patil, Finite element approach to study the elastic instability of concrete filled steel tubular column under axial loads. Int. J. Emerg. Technol. Adv. Eng. 2, 276–284 (2012)

    Google Scholar 

  30. J.M. Portoles, E. Serra, M.L. Romero, Influence of ultra-high strength infill in slender concrete-filled steel tubular columns. J. Constr. Steel Res. 86, 107–114 (2013)

    Article  Google Scholar 

  31. X. Qu, Z. Chen, G. Sun, Experimental study of rectangular CFST columns subjected to eccentric loading. Thin-Walled Struct. 64, 83–93 (2013)

    Article  Google Scholar 

  32. K. Sakino, H. Nakahara, S. Morin, I. Nishiyama, Behavior of centrally loaded concrete-filled steel-tube short columns. J. Struct. Eng. 130, 180–188 (2004)

    Article  Google Scholar 

  33. M. Saridemir, Prediction of compressive strength of concretes containing metakaolin and silica fume by artificial neural networks. Adv. Eng. Softw. 40, 350–355 (2009)

    Article  MATH  Google Scholar 

  34. J. Schmidhuber, Deep learning in neural networks: an overview. Neural Netw. 61, 85–117 (2015)

    Article  Google Scholar 

  35. S.P. Schneider, Axially loaded concrete-filled steel tubes. J. Struct. Eng. 124, 1125–1138 (1998)

    Article  Google Scholar 

  36. H.K. Sen (1969) Triaxial Effects in Concrete-Filled Tubular Steel Columns. Ph.D. thesis, University of London, England (1969)

  37. N.E. Shanmugam, B. Lakshmi, State of the art report on Steel Concrete Composite Columns. J. Constr. Steel Res. 57, 1041–1080 (2001)

    Article  Google Scholar 

  38. I.B. Topcu, M. Saridemir, Prediction of properties of waste AAC aggregate concrete using artificial neural network. Comput. Mater. Sci. 41, 117–125 (2007)

    Article  Google Scholar 

  39. SNNS (Stuttgart Neural Network Simulator) software simulator for neural networks. http://www.ra.cs.uni-tuebingen.de/SNNS/. Accessed 2 May 2015

  40. X.M. Yu, B.C. Chen, A statistical method for predicting the axial load capacity of concrete filled steel tubular columns. Int. J. Civ. Environ. Eng. 20, 20–39 (2011)

    Google Scholar 

Download references

Acknowledgements

Technical supports for this study provided by the Department of Civil Engineering, National Institute of Technology, Tiruchirappalli, Tamil Nadu, India, is gratefully acknowledged. The authors thank Government of India, Ministry of Human Resource Development—Department of Higher Education, for the Ph.D. scholarship given to the research scholar to carry out the research work.

Author information

Authors and Affiliations

  1. Department of Civil Engineering, National Institute of Technology, Tiruchirappalli, Tamil Nadu, India

    S. Jayalekshmi, J. S. Sankar Jegadesh & Abhishek Goel

Authors
  1. S. Jayalekshmi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. S. Sankar Jegadesh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Abhishek Goel
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Jayalekshmi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jayalekshmi, S., Jegadesh, J.S.S. & Goel, A. Empirical Approach for Determining Axial Strength of Circular Concrete Filled Steel Tubular Columns. J. Inst. Eng. India Ser. A 99, 257–268 (2018). https://doi.org/10.1007/s40030-018-0291-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40030-018-0291-x

Keywords

Search

Navigation