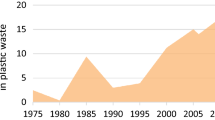
Abstract
Every year tones of plastic are produced and people become the victim of many types of waste including domestic, agronomic and industrialized waste. In this paper, we have constructed the mathematical model to examine the rising pollution level due to industrial plastic waste and the process of destroying or renovating this plastic waste using several toxic chemicals. The dynamical model suggests investing the influential part of the budget into civilization health policy, like reducing the plastic burning and support the installation of the eco-friendly plastic recycling machine to reuse dumped industrial plastic. Both of these policies are strides to the health as well as the economic progress of the country. In the model, the local stability of the system of nonlinear differential equations is qualitatively analyzed with appropriate conditions. Graph theory results help to distinguish the global stability behavior of the model. Techniques to reduce plastic pollution are outlined by optimizing both the policies which are simulated numerically with given validated data.








Similar content being viewed by others
References
Branicky MS, Borkar VS, Mitter SK (1998) A unified framework for hybrid control: model and optimal control theory. IEEE Trans Autom Control 43(1):31–45
Cairns CN (2005). E-waste and the consumer: improving options to reduce, reuse and recycle. In Proceedings of the 2005 IEEE international symposium on electronics and the environment, 2005. pp 237–242
De Pillis LG, Radunskaya A (2001) A mathematical tumor model with immune resistance and drug therapy: an optimal control approach. Comput Math Methods Med 3(2):79–100
Ding C, Tao N, and Zhu Y (2016) A mathematical model of Zika virus and its optimal control. In: 2016 35th Chinese control conference (CCC) pp 2642–2645
Donovan RC, Rabe KS, Mammel WK, Lord HA (1975) Recycling plastics by two-shot molding. Polym Eng Sci 15(11):774–780
Dubey B (2010) A model for the effect of pollutant on human population dependent on a resource with environmental and health policy. J Biol Syst 18(03):571–592
Fleming W, Lions PL (eds) (2012) Stochastic differential systems, stochastic control theory and applications: proceedings of a workshop, vol 10, held at IMA, June 9–19, 1986. Springer
Gaff H, Schaefer E (2009) Optimal control applied to vaccination and treatment strategies for various epidemiological models. Math Biosci Eng 6(3):469
Harary F (1969) Graph theory
Matar N, Jaber MY, Searcy C (2014) A reverse logistics inventory model for plastic bottles. Int J Logist Manag 25(2):315–333
Nganda MK (2007) Mathematical models in municipal solid waste management
Okosun KO, Makinde OD (2014) A co-infection model of malaria and cholera diseases with optimal control. Math Biosci 258:19–32
Pathinathan T, Ponnivalavan K (2014) The study of hazards of plastic pollution using induced fuzzy cognitive maps (IFCMS). J Comput Algorithm 3:671–674
Pontryagin LS, Boltyanskii VG, Gamkrelidze RV, Mishchenko EF (1986) The mathematical theory of optimal process. Gordon and Breach Science Publishers, New York, pp 4–5
Rachah A, Torres DF (2015) Mathematical modelling, simulation, and optimal control of the 2014 Ebola outbreak in West Africa. Discrete Dyn Nat Soc 15:842792
Rodrigues HS, Monteiro MTT, Torres DF (2014) Vaccination models and optimal control strategies to dengue. Math Biosci 247:1–12
Shah NH, Jayswal EN, Satia MH (2019) Optimal investments for burning and recycling of plastics. Adv Water Environ Eng 1(1):1–9
Song HS, Moon KS, Hyun JC (1999) A life-cycle assessment (LCA) study on the various recycle routes of PET bottles. Korean J Chem Eng 16(2):202–207
Swan GW (1990) Role of optimal control theory in cancer chemotherapy. Math Biosci 101(2):237–284
West DB (1996) Introduction to graph theory, vol 2. Prentice hall, Upper Saddle River, NJ
Wilcox C, Van Sebille E, Hardesty BD (2015) Threat of plastic pollution to seabirds is global, pervasive, and increasing. Proc Natl Acad Sci 112(38):11899–11904
Acknowledgements
All authors are thankful to DST-FIST file # MSI-097 for technical support to the department of Gujarat University. Second author is funded by UGC granted National Fellowship for Other Backward Classes (NFO-2018-19-OBC-GUJ-71790) and third author is funded by a Junior Research Fellowship from the Council of Scientific & Industrial Research (file no. 09/07(0061)/2019-EMR-I).
Author information
Authors and Affiliations
Corresponding author
Additional information
Editorial responsibility: S. R. Sabbagh-Yazdi.
Rights and permissions
About this article
Cite this article
Shah, N.H., Jayswal, E.N. & Suthar, A.H. Mathematical modeling on investments in burning and recycling of dumped waste by plastic industry. Int. J. Environ. Sci. Technol. 18, 741–750 (2021). https://doi.org/10.1007/s13762-020-02839-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13762-020-02839-1