1 Introduction

Radial growth and wood anatomy are of major importance for both tree functioning and industrial wood production and quality (Macdonald and Hubert 2002; Vaganov et al. 2006). Wood formation involves production and growth of new cells by the cambium and their subsequent differentiation. In temperate climate, cambium activity is seasonal, resulting in a tree-ring made of differentiated cells. In conifers, tree rings present a clear anatomical structure: narrow and thick latewood cells follow large and thin earlywood cells.

The regulation of cambial activity and of final wood characteristics throughout the years makes trees able to acclimate to a wide range of environmental conditions (Agusti and Greb 2013) and is therefore thought to be responsive to climate changes. However, the tree-ring structure is surprisingly stable compared to other tree characteristics under environmental control (Balducci et al. 2016).

Although variations in tree growth, tree-ring structure, and wood quality are well studied, described, and quantified over many species, sites, and years, still very little is known about the intrinsic mechanisms that produce these features (Vaganov et al. 2006; Cuny et al. 2013).

During the growing season, the forming wood presents a striped pattern composed of (1) a division zone (also called the cambial zone sensu stricto), where cells undergo growth and division; (2) an enlargement zone, where cells experience growth without division; (3) a maturation zone (also called the thickening zone), where fully grown cells undergo secondary wall deposition and cell-wall lignification; and finally (4) a mature zone, composed of fully functional xylem cells, which have passed through programmed cell death (Fig. 1b) and progressively build the annual tree-ring (Wilson 1984).

Fig. 1
figure 1

Wood results from the regulated activity of the cambium. a Cross-section of a conifer stem. The vascular cambium is a thin layer of undifferentiated cells producing both xylem and phloem tissues. b Cross-section of forming xylem. Along the radial files of cells, a zonation pattern can be observed: CZ, EZ, TZ, MZ. Here, mature cells cannot be distinguished from thickening cells. c Anatomical characteristics of a tree-ring formed, from Cuny et al. (2014). d Auxin concentration gradient across a wood-forming tissue, from Bhalerao and Fischer (2014). According to the morphogenetic gradient hypothesis, auxin concentrations higher than threshold T1 correspond to the cell division zone, concentrations between T1 and T2 to the cell expansion zone and below T2 to secondary cell wall formation (SCW)

Full size image

Cambial activity is thus under a tight spatial-temporal control. This can be revealed experimentally when cambial cells are put into culture, or when major wounds disturb the spatial arrangement of the cell rays (Barnett 1978). In both cases, cell proliferation becomes erratic and a callus with exponential growth and no wood-ring formation is observed. On the contrary, an intact cambium displays a typical growth curve (e.g. Zeide 1993) with a long period of almost steady growth rate (steady growth) emerging from a controlled combination of cell division and enlargement processes, whereas the typical final anatomical pattern—large and thin earlywood cells followed by narrow and thick latewood cells (Fig. 1c)—of mature tree-rings emerges from enlargement and thickening processes.

Because a complex spatial-temporal developmental process is involved, models appear to be central tools to get insight into the major mechanisms controlling wood-ring formation. However, few models of cambial activity have been developed so far. They are primarily concerned with the dynamics of carbon allocation and water potential within the tree (Deleuze and Houllier 1998; Vaganov et al. 2006; Hölttä et al. 2010; Wilkinson et al. 2015; Drew and Downes 2015); some of them also include an explicit biophysical description of cell growth and division (e.g. Hölttä et al. 2010; Drew and Downes 2015). But all of them assume fixed ad hoc rules for the succession of cell-differentiation phases. Additionally, most of the cambial models focus on the influence of the environmental factors on the resulting tree radial growth and wood quality, without any validation of the processes involved in the model at the cellular level. There is a lack of models capturing the spatial-temporal interactions between meristematic cells and morphogenetic signals, although this kind of models has been instrumental in deciphering the dynamics of shoot and root apical meristems and assessing mechanistic control hypotheses (Grieneisen et al. 2007; Traas and Monéger 2010).

The consistent spatial zonation exhibited by wood-forming tissue suggests the existence of a signal providing each differentiating cell with information about its relative position within the tissue, following ideas first introduced by Wolpert (1969). It has been argued that such positional information could be provided to cells in the form of a concentration gradient of a morphogen (Bhalerao and Bennett 2003).

Multiple observations of a graded concentration profile of auxin spanning over the whole wood-forming tissue and peaking in the cambial zone (Tuominen et al. 1997; Uggla et al. 1996; Uggla et al. 1998; Uggla et al. 2001) (see Fig. 1d) has led some authors to propose that auxin acts as a morphogen for cambial activity, and that its gradient provides enough positional information for a partitioning into the distinct differentiation zones (Sundberg et al. 2000; Bhalerao and Bennett 2003). Variations in the shape of the gradient through the xylem would then account for changes in cell numbers and final sizes.

Auxin has a unique way of polar transcellular transport (Polar Auxin Transport, PAT) involving active transporters —the most studied being the auxin exporters of the PIN family. Because of the specific transport of auxin, two general hypotheses have been formulated on how an auxin gradient can be established and maintained in a developing tissue. On the one hand, Schrader et al. (2003) suggested that polar auxin transport is directly involved in controlling gradients. On the other hand, Bhalerao and Fischer (2014) conjectured that the advection of auxin due to the growth-induced cell flow could be sufficient to account for the observed auxin gradients across wood-forming tissues (advection refers to the directed transport driven by the bulk movement of the medium generated by growth and fluid flow). Indeed, growth has been shown to alter signal transport and distribution through advective but also dilutive effects (Crampin et al. 2002; Baker and Maini 2007; Merret et al. 2010; Band et al. 2012). Moreover, when polar transport at the cell membrane is involved, such as with auxin, cell expansion and division change the density of membranes and, consequently, the local transport of morphogens (Laskowski et al. 2008). Such effects can lead to unexpected feedbacks and non-intuitive interactions between signal transport and growth (especially for auxin, which has itself a huge effect on growth), whose investigation requires the use of a multicellular, quantitative, and dynamic model.

Several multicellular models of auxin gradient formation have been developed for the root tip (Grieneisen et al. 2007; Muraro et al. 2013) and the shoot apical meristem (Smith et al. 2006), but not for the cambium. This absence is surprising given that auxin gradients were first measured across wood-forming tissues (Sundberg et al. 2000) whereas in root and shoot meristems, auxin measurements have still not reached the spatial resolution required for distinguishing between zones of cell differentiation (Bhalerao and Fischer 2014). Besides, outside the cambial zone, the developing wood has a very low capacity to synthesise auxin (Schrader et al. 2003), so that all the auxin present in the enlargement zone and the following zones has been produced in the cambial zone or transported to it.

Finally, auxin is not the only candidate for a cambial morphogen. Nilsson et al. (2008) found that the expression of most of the auxin-responsive genes was only poorly correlated with the auxin concentration gradient. Thus, the action of auxin on cell behaviour may be less straightforward than originally expected. Consequently, focus has been recently turned to signalling by small peptides. In particular, the peptide TDIF (tracheary element differentiation inhibitory factor), under the control of CLAVATA-like gene family, which is known to enter the cambium from the phloem and to be involved in vascular stem cell maintenance (Hirakawa et al. 2008; Hirakawa et al. 2010; Etchells et al. 2013), could also act as a morphogen. Contrary to auxin, TDIF is likely to diffuse passively and exclusively in the network of cell walls (called the apoplast).

In this study, we investigated the explanatory power of the morphogenetic-gradient hypothesis in wood formation. More specifically, we tested several mechanistic hypotheses, reflecting the involvement of possible signals transported from the cambium-phloem side. We addressed the following questions:

  1. 1.

    Can diffusion and/or polar transport mechanisms generate a morphogenetic gradient that leads to a steady radial growth, consistent with measurements of stem girth increase? Is growth advection and/or dilution a significant part of this process?

  2. 2.

    Can a morphogenetic gradient ensure a proper spatial zonation in the developing tissue?

  3. 3.

    Can a morphogenetic gradient create the typical cell size pattern of conifer tree-ring structure?

To answer these questions, we have developed a computational model of wood formation in conifers based on the morphogenetic-gradient theory and we have confronted its predictions to data produced by wood formation monitoring studies (e.g. Cuny et al. 2013).

2 Materials and methods

2.1 Generic traits upon which the model will be assessed

Before detailing the hypotheses and equations of the model, it is necessary to define its outputs, and to detail the traits upon which its predictions will be assessed, and possibly falsified versus experimental data. These traits belong to three categories: (i) tree radial growth, (ii) intra-annual dynamics of xylogenesis, and (iii) tree-ring structure and tracheid dimensions.

Tree radial growth

In temperate or cold climates, tree-stem radius and tree-ring width generally follow a S-shaped curve when monitored over the whole growing season (Fig. 2a). After a slow start, the rate of xylem growth increases exponentially over the spring, until it reaches a maximum around the summer solstice (Rossi et al. 2006b). Then, the rate decreases regularly over the summer and cambial activity finally ceases at the beginning of autumn. Classically, the ‘decline’ of the initial exponential expansion is mathematically described using a Gompertz function (Camarero et al. 1998; Rossi et al. 2003). An ad hoc “decline module” intervenes in the equation of the Gompertz function:

$$ \frac{1}{R(t)} \frac{\mathrm{d}R(t)}{\mathrm{d}t} = \underbrace{\alpha}_{\text{expansion}} - \underbrace{\kappa\ln\left( R(t)\right)}_{\text{decline}}. $$
(1)

Theoretical ecologists classically interpret this decline module as the effect of the increase of competition for limited resources (e.g. space, light, sugar, nutrients) accompanying any growing population (Zeide 1993; 2003). However, at the level of the cambium, the shortage of resources is not that clear, due to reserves stored in the wood-ray cells (Silpi et al. 2007). And the way the intrinsic exponential trend of cell number and overall diameter size in a dividing-expanding stem cell population is channelled for a while into a steady linear growth (constant growth rate) during the end of spring (Fig. 2a) remains unclear.

Fig. 2
figure 2

Cumulative radial growth and cell numbers of Scots pine (Pinus sylvestris) through a growing season. a Stem radial growth obtained by microcores. Data courtesy from Alice Michelot, published in Michelot et al. (2012). b Number of cells in the cambial, enlargement and thickening zones. Data courtesy from Henri Cuny, published in Cuny et al. (2013)

Full size image

Intra-annual dynamics of xylogenesis

The coordinated temporal succession of the cell differentiation phases for all the radial files creates distinct characteristic stripe-like zones of development in the forming xylem (Fig. 1b). This global zonation pattern persists over the growing season, although the width of each individual developmental zone —classically quantified by the number of cells belonging to it (Rossi et al. 2006a)— is variable and follows characteristic seasonal dynamics (Cuny et al. 2013). Generally, the number of cells in the cambial and enlargement zones both follow bell-shaped curves skewed to the left (Cuny et al. 2013) (Fig. 2b). The numbers of cambial and enlarging cells rapidly increase at the beginning of the growing season, after which they decrease slowly until entrance in dormancy. By contrast, the number of cells in the thickening phase follows a right-skewed bell-shaped curve. The number of mature cells approximately follows a Gompertz curve (Cuny et al. 2013) (not shown).

Tree-ring structure and tracheid dimensions

Most of the conifers share the same typical tree-ring structure (Fig. 1c). From the center to the periphery of the stem, there is a transition from large, thin-walled cells of light earlywood, produced at the beginning of the growing season, to narrow, thick-walled cells of dense latewood, produced at the end of the growing season. Earlywood represents generally c. 40 % of a tree-ring, while transition wood is more variable and represents about 20 %, leaving the last 40 % of a ring to latewood. A regular decrease in cell radial diameter is generally observed from the beginning to the end of a ring; the first earlywood cells are commonly about three times larger (c. 45 μm) than the last latewood cells (c. 15 μm). On the other hand, the tangential cell size is almost constant all along a ring (c. 35 μm). Therefore, resulting S-shaped density profiles present minimal values in earlywood and maximum values in latewood (Fig. 1c).

2.2 Model presentation

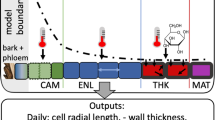
Since there are multiple potential transport mechanisms and boundary conditions involved, we have developed various models, which are organised into a family called XyDyS (Xylogenesis Dynamics Simulators). They all share a common core, which includes cell division and enlargement processes, along with the consequences for morphogen transport, and the assumption that the studied signal provides positional information to the differentiating cells and determines the growth rate of each cell. Complementing this common core, stand two adjustable elements (Fig. 3). The first one specifies the transport mechanism, either diffusion or polar transport. The second one specifies the boundary conditions, i.e. the source and the sink of the signal. Each member of the XyDyS model-family then corresponds to a different association of transport mechanism and boundary conditions.

Fig. 3
figure 3

General diagramme of XyDyS. XyDyS core defines the structure common to all XyDyS models. Each signal transport mechanism comes as a module that can be clipped to the core. The boundary condition on the xylem side comes as another module, clipped to the transport module. For instance, model a would be used to investigate the action of a signal which diffuses in the apoplast, with mature xylem flushing out the signal. Model b would be used to investigate the action of a signal which is polarly transported, with a mature xylem impenetrable to the signal

Full size image

The core of the model

XyDyS models are one-dimensional and consider a single file of differentiating cells (Fig. 4). This geometrical simplification is justified by the symmetry of the xylem tissue. The file is composed of the cells, which (within a given growing season) either differentiate into tracheids (possibly after one or more division cycles) or remain cambial at the end of the season. The first boundary of the system (‘the cambium boundary’) is the interface with the part of the cambium, which differentiates into phloem. The second boundary (‘the mature-xylem boundary’) is the interface with the mature xylem produced during the previous year. Within a file, cells are indexed from i = 1, at the cambium boundary, to i = N(t), at the xylem boundary, with N(t) being the number of cells in the file at time t. Each cell is geometrically characterised by its length L i (t). There are initially N 0 cells in the file, with all the same length L init (initial condition).

Fig. 4
figure 4

Schematic layout of a XyDyS simulation. The gradient of signal concentration (blue dots) imposes both cell identities and growth rates. Cells with a concentration above the division threshold (T d ) have the ability to divide. Cells with a concentration above the enlargement threshold (T e ) are growing, with a growth rate proportional to the concentration. The zonation is based on cell identity and geometry. Cambial zone (CZ, green): small (L i <2L i n i t ) growing cells. Enlargement zone (EZ, blue): large (L i >2L i n i t ) growing cells. Thickening zone and mature zone (TZ + MZ, red): non-growing cells

Full size image

A signal is present throughout the file, with a variable concentration profile. C i (t) denotes the average concentration of signal within the cell i. C i (t) is interpreted by the cells as a positional information, based on a French-flag model (Wolpert 1969). We defined two concentration thresholds: the division threshold, T d , and the enlargement threshold, T e , with T d >T e . The identity of any cell i is governed by the following rules:

  • If C i ≥T d , the cell enlarges and is able to divide.

  • If C i <T d and C i ≥T e , the cell enlarges but is not able to divide.

  • If C i <T e , the cell no longer enlarges.

Although the mechanical force for cell enlargement comes from turgor pressure, this process is controlled by cell wall extensibility (Cosgrove 2005). We assume that the signal also acts on wall extensibility, and thus controls the growth rate of those cells which are able to enlarge. More precisely,

$$ \frac{1}{L_{i}(t)} \frac{\mathrm{d}L_{i}(t)}{\mathrm{d}t} = k_{g} C_{i}(t), $$
(2)

where k g is a proportionality constant, in s−1. The cell growth rate \(\frac {1}{L_{i}(t)}\frac {\mathrm {d}L_{i}(t)}{\mathrm {d}t}\) is actually a growth-induced strain rate (Moulia and Fournier 2009); in what follows, it will be denoted by \(\dot {\epsilon }_{i}(t)\).

Cell division follows a simple criterion: if a cell has an identity that allows division, it divides when reaching a threshold length defined as twice its initial length. The assumption of a threshold length for division is supported by the probable existence of a cell size checkpoint at the G1-S transition (Schiessl et al. 2012). Moreover, analyses of cell size distribution along the growth zone of developing roots (Beemster and Baskin 1998) and leaves (Fiorani et al. 2000) suggest that all cells in a given meristem divide in half at the same length.

Experimentally, the developmental zones are defined based on visual criteria. In order to be able to compare the outputs of XyDyS models with data, we followed similar criteria, ascribing ‘apparent status’ to virtual cells. Cambial cells were defined as growing cells that were smaller than two times the diameter of a newly created cell (L i <L init). Enlarging cells were growing cells larger than two times the diameter of a newly created cell (L i >L init). Wall-thickening and mature cells were no longer growing cells (Fig. 4).

Transport mechanisms

As stated before, two different transport mechanisms were modeled in XyDyS and used for simulations.

Let us first consider continuous diffusion in the apoplast. The cambium boundary of the file is located at x = 0 and the xylem boundary at x = L(t), where L(t) is the total length of the file at time t. The concentration profile is then modelled as a continuous function of the space, C(x,t), which obeys a diffusion-decay transport mechanism (Wartlick et al. 2009; Grieneisen et al. 2012). The velocity field associated with the growth of the file is given by (Skalak et al. 1982)

$$ v(x,t) = \frac{\mathrm{d}x}{\mathrm{d}t}. $$
(3)

The strain rate is related with this velocity field through the following equation:

$$ \dot{\epsilon}(x,t) = \frac{\partial v(x,t)}{\partial x}. $$
(4)

In accordance with what we stated above, \(\dot {\epsilon }(x,t)\) is uniform within each cell and is defined by the discrete list \(\{\dot {\epsilon }_{i}(t)\}_{i=1,\ldots ,N(t)}\). We can now write the growth-diffusion-decay equation governing the concentration profile (Crampin et al. 2002; Baker and Maini 2007):

$$\begin{array}{@{}rcl@{}} \frac{\partial C(x,t)}{\partial t} &+& v(x,t)\frac{\partial C(x,t)}{\partial x} = D\frac{\partial^{2}C(x,t)}{\partial x^{2}} \\&-& \mu C(x,t) - \dot{\epsilon}(x,t) C(x,t). \end{array} $$
(5)

D is the diffusion coefficient (in μm2s−1) and μ is the decay rate (in s−1).

Let us now consider polar active transport. We assume that concentration gradients within cytoplasms of the cells are negligible compared to concentration differences between neighbouring cells. The concentration profile is then modelled as a discrete function of the space, {C i } i=1,…,N , which takes a single value on each cell. Transport occurs as fluxes between cells. The signal crosses cell membranes either passively or by mean of special carriers.

We use a model of fluxes similar to the ‘unidirectional transport mechanism’ from Grieneisen et al. (2012). Carriers are assumed to have a constant and equal density on all membranes. We also assume that all carriers have the same polarity along the file. This polarity is directed toward either the xylem or the cambium.

If carriers are polarised toward the cambium for example, the flux from cell i to cell i + 1 only relies on permeability, so it writes as F i,i + 1 = q C i , where q is the permeability rate (in μm s−1). The opposite flux from cell i + 1 to cell i is F i + 1,i = (p + q)C i+1, where p (in μm s−1) accounts for the action of polar carriers. The dynamic changes in C i are described as

$$ \frac{\mathrm{d}C_{i}}{\mathrm{d}t} = \frac{1}{L_{i}} \left[F_{i-1,i} -\! F_{i,i-1} + F_{i+1,i} \!- F_{i,i+1}\right] - \mu C_{i} - \dot{\epsilon}_{i} C_{i}, $$
(6)

or

$$ \frac{\mathrm{d}C_{i}}{\mathrm{d}t} = \frac{1}{L_{i}} q C_{i-i} - \frac{1}{L_{i}} (p + 2q) C_{i} - \mu C_{i} - S_{i} C_{i} + \frac{1}{L_{i}} (p+q) C_{i+1}. $$
(7)

Following the same logic, a flux equation can be derived if carriers are polarised toward the xylem. Note that Eqs. 6 and 7 do not hold for C 1 and C N , which depend on the boundary conditions.

Boundary conditions

The signal is assumed to enter the file from the cambium boundary. Accordingly, we imposed the concentration of the signal at the cambium boundary of the file. At the xylem boundary, two different conditions are possible depending on the signalling molecule. If the molecule can freely enter the mature xylem, then it is flushed out by the ascending sap flux. In this case, we model the xylem as an absorbing sink, with a zero-concentration boundary condition. Conversely, if the molecule cannot enter the mature xylem, then we model the mature xylem boundary as an impermeable barrier, with a zero-flux boundary condition. These two boundary conditions were tested alternatively in our investigation depending on studied morphogen (as detailed later on) (Tables 1 and 2).

Table 1 List of state variables
Full size table
Table 2 List of parameters
Full size table

2.3 Implementation and visualisation of simulations

Transport equations have been numerically solved using an explicit Euler method. In growing cells, new discretisation nodes are regularly added in the model so that the Courant–Friedrichs–Lewy stability condition is always satisfied. This numerical method has been implemented in the Python programming language, using the NumPy library (van der Walt et al. 2011). The exploration of XyDyS model simulations were partly performed using the IPython software (Pérez and Granger 2007). We have also developed a graphical user interface dedicated to XyDyS models with Traits and TraitsUI libraries by Enthought (https://enthought.com/). XyDyS model simulations are visualised using the graphical convention explained in Fig. 4.

3 Results

3.1 A morphogenetic signal can control the volumetric growth of the developing xylem

Continuous diffusion

We first assumed that the signal is not degraded (μ = 0) and diffuses fast enough so that dilution and advection due to cell growth can be neglected (steady-state approximation, \(\dot {\epsilon }(x,t) = 0\)). The concentration was set to zero at the xylem boundary. Under these conditions, the concentration profile was a straight line joining both boundary concentrations of the cell file (Fig. 5a and S1 Video). Thus, it depended only on the distance between the two ends of the file: the longer was the file, the flatter was the profile. Thus, the growth of the file flattened the profile. And the flatter the profile was, the larger the cambial and enlargement zones were. Therefore, the cambial and enlargement zones increased in size in the same proportion as the whole file. The growth was thus exponential and the system diverged (Fig. 6a). Under these conditions, the morphogenetic gradient proved to be unable to provide a reliable information for controlling the growth of the tissue.

Fig. 5
figure 5

Three possible concentration profiles using XyDyS-DIF with fixed boundary conditions and parameters. a Without decay and with negligible dilutive effect. The profile is linear and depends on the total length of the file: The longer the file, the flatter the profile. b With decay and negligible dilutive effect. The profile reaches a stationary exponential shape. c With non-negligible dilutive effect and without decay. The profile reaches a stationary exponential shape only in the growing part of the file (CZ + EZ)

Full size image
Fig. 6
figure 6

Growth of a cell file regulated by a diffusible signal. a Without decay and with negligible dilutive effect. The growth is exponential. b With decay and negligible dilutive effect. The growth becomes linear after an initial exponential phase. c With non-negligible dilutive effect and without decay. Again, the growth becomes linear

Full size image

The fundamental problem of that situation was that the distance on which the gradient was acting increased with the size of the system. There was no constant characteristic length in the distribution of the signal, so it could not provide a relevant positional information to the cells.

We then set a non-zero decay rate while holding the steady-state approximation. The concentration profile then presented an analytical form, which depended on the length of the cell file relatively to the characteristic length associated with the diffusion–decay mechanism. This characteristic length is expressed as:

$$ \lambda_{d}=\sqrt{\frac{D}{\mu}}. $$
(8)

As the file becomes long compared to λ d , the profile reaches a stationary exponential shape (Fig. 5b and S2 Video), given by the equation:

$$ C(x) = C_{0} \exp\left( -\frac{x}{\lambda_{d}}\right). $$
(9)

Consequently, the growing part of the file (cambial and enlargement zones) kept a fixed length, and thus the overall growth became linear in time (Fig. 6b). In this situation, the growth speed depended linearly on the concentration C 0 and on the characteristic length λ d .

We then tested the opposite setting: No decay (μ = 0), but a signal which does not diffuse fast enough to counter the growth-induced dilution. In Eq. 5, the growth rate plays the same role as an apparent non-uniform and non-constant decay rate. The dilution induced by the growth balanced the unloading of signal from the phloem. As a result, the concentration profile became stationary where the cells were growing (Fig. 5c and S3 Video). Again, this led to a constant growth speed (Fig. 6c). This means that growth alone can stabilise a gradient if the gradient is itself the cause of the growth.

In a realistic case, both decay and dilution may play a role in shaping a morphogenetic gradient. But the relative significance of each factor depends on the particular signal and tissue properties. The decay effect is relevant if λ d is of the same order of magnitude as the size of the growing tissue. Exhibiting a similar criterion for the dilutive effect is not as straightforward, since there is no analytical formula for the concentration profile. However, we propose an equivalent to λ d , expressed as follows:

$$ \lambda_{g}=\sqrt{\frac{D}{\dot{\epsilon}_{c}}}, $$
(10)

where \(\dot {\epsilon }_{c}\) is a characteristic growth rate. A relevant choice for \(\dot {\epsilon }_{c}\) is the growth rate at the division threshold, i.e. \(\dot {\epsilon }_{c} = k_{g}T_{d}\). The dilutive effect due to growth is significant when λ g is of the same order of magnitude as the size of the growing tissue.

Polar active transport

First, we assumed that carriers were oriented toward the xylem. In that configuration, the signal was ‘pumped’ from the cambium to the differentiating cells. This led to an accumulation of signal as the sink was pushed away (i.e. advected) by the growth (Fig. 7a and S4 Video). The growing part of the file inflated without limit and the global growth diverged exponentially.

Fig. 7
figure 7

Two possible concentration profiles using XyDyS-PAT with fixed boundary conditions and parameters. a, b With carriers oriented toward the xylem. Auxin is ‘pumped’ in the file and accumulates. As a consequence, the cambial and enlargement zones expand limitless. c, d With carriers oriented toward the cambium. Auxin is confined near the cambial zone and the concentration profile reaches a stationary exponential shape

Full size image

As a second assumption, carriers were oriented toward the cambium, and thus countered the diffusion of the signal away from the source. As shown in Fig. 7b and S5 Video, the concentration profile was then approximately exponential near the cambium. Strictly speaking, the profile was not stationary since cell growth and division caused both continuous and sharp changes in the local density of carriers. However, signal concentration fluctuations around the average profile were small and the growth remained linear in time.

3.2 A gradient can control the number of cells in the cambial and enlargement zones

We then investigated how the number of cells in each developmental zone can be controlled by a gradient of signal. We focussed on the exponential gradients generated by diffusion and decay, in the steady-state approximation.

Transient state

We have seen that once an exponential stationary gradient had been established, the size of the growing part of the file (cambial + enlargement zones) was quite constant. But before reaching this steady state, the system went through a transient state whose features are of interest for our understanding of the dynamics of the cambium. The type of boundary condition imposed on the xylem boundary crucially matters here.

When a zero-concentration boundary condition was imposed, cell numbers slowly increased toward their stationary values (Fig. 8a). On the contrary, when a zero-flux boundary condition was imposed, cell numbers increased very rapidly to a maximum before decreasing toward their stationary values (Fig. 8b). This initial ‘burst’ was caused by the signal filling in the cell file while the file was still shorter than the characteristic length of the gradient. It could account for the sudden onset of growth as observed at the beginning of the growing season. Note that this effect is intrinsic to the dynamics of the cambium and does not depend on any external driving force.

Fig. 8
figure 8

Cell numbers with constant parameters and boundary conditions. a With a zero-concentration boundary condition on the xylem side. b With a zero-flux boundary condition on the xylem boundary. Cell numbers reach the same stationary state in both cases, but the initial transient states are different. With a zero-concentration boundary condition (a), cell numbers increase steadily and slowly toward their final state. With a zero-flux boundary condition (b), cell numbers increase rapidly up to a maximum and then decrease rapidly toward their final state

Full size image

Steady state

In the steady state, the lengths of the cambial and enlargement zones were dictated by the shape of the concentration profile. This shape depended on two parameters: The concentration imposed on the cambium boundary, C 0, and the characteristic length, λ d . A change in C 0 caused a proportional change in the number of cambial cells (provided that C 0 was above the division threshold), but very little change in the number of enlarging cells. This was not realistic. Indeed in the observational data, the trend in the number of enlarging cells closely follows the trend in the number of cambial cells (Fig. 2b).

Alternatively, tuning the value of λ d could lead to parallel variations in the numbers of cambial and enlarging cells, in better agreement with the observations. According to Eq. 8, such a change in λ d can be achieved through a change in the decay rate of the signal, μ, which is presumably under enzymatic (and hence genic) control. The gradient expands as μ decreases. Therefore, it can be hypothesised that the zonation is controlled by λ d , through the decay rate.

Controlling the variations in cell numbers over the growing season

Our model showed that a tuning of the characteristic length λ d is sufficient to account for the main features of the variations of cell numbers in the cambial and enlargement zones through a growing season. To do so, we set a zero-flux boundary condition on the xylem boundary and imposed a constant concentration on the cambium boundary. At the beginning of the growing season, λ d was set small in order to restrain the initial burst; then, λ d was increased to sustain the growth; finally, λ d was steadily decreased. The results of that simulation (Fig. 9a) were globally in agreement with the experimental observations (Fig. 9b).

Fig. 9
figure 9

Cell numbers through a growing season. a As simulated by the model. b As experimentally reported in (Cuny et al. 2013). The model reproduces the first half of the seasonal pattern, but it cannot account for the final decline of the enlargement zone

Full size image

Although the former variation pattern of λ d can be said to be ‘ad hoc’, this at least shows that it is possible to reach a realistic control of cell numbers in the various zones by a biological control of the characteristic length of the morphogenetic gradient.

3.3 A morphogenetic gradient fails at reproducing tree-ring structure

Figure 10 shows the final cell diameters obtained from the same simulation run as in Fig. 9a. Two observations can be readily made.

  1. 1.

    The characteristic pattern of the final cell size, as shown in Fig. 1c, was not reproduced by our model. Actually, there was no global trend at all in the simulated diameters. Large changes in the size of the cambial and enlargement zones had no effect on the size of the produced cells. Therefore, the pattern of cell number variations does not imply by itself the pattern of final cell diameters. Positional information is not sufficient for controlling the final size of the cells.

  2. 2.

    Diameters oscillated, with sharp changes in the mean value of the oscillations. This behaviour does not match any observation and was totally unexpected. A deeper analysis showed that this feature is inherent to a single gradient controlling both the zonation and the growth rate. More precisely, it comes from the fact that cells cease to enlarge at a fixed position along the file, while the position of the beginning of the enlargement phase fluctuates (see S1 Text).

Fig. 10
figure 10

Final cell diameters of a cell file regulated by a diffusion-driven gradient. Cells are indexed from the innermost (xylem) boundary on, following the representation of Fig. 1c. Diameters display oscillations with a large amplitude

Full size image

4 Discussion

The morphogenetic-gradient hypothesis theory has been commonly regarded as a probable explanation for the emergence of the characteristic patterns observed in wood formation and in the resulting tree-ring structure. However, it has remained speculative. Neither the underlying biological mechanisms involved have been totally unveiled nor its dynamics has been fully assessed using computational models and their comparison to experimental results. In this work, we filled the latter gap with a careful analysis of the explanatory power of the morphogenetic-gradient hypothesis, following a parsimonious modelling approach. Although the biological example considered here were auxin and TDIF, our analysis holds also for any other potential signal with a phloem-bound source. This analysis yielded three major insights.

i) Both diffusion and polar transport are able to establish a stationary concentration profile within the wood-forming tissue. Such a profile ensures that the growth is steady and responds linearly to the concentration imposed by the source at the cambium boundary. However, some conditions have to be met in order to form a plausible morphogenetic gradient. A diffusible signalling molecule must have either a sufficiently high decay rate or a sufficiently low diffusion coefficient. We showed that growth-induced dilution alone could be strong enough to make a concentration profile stationary. This effect can be thought as a negative feedback loop, in which the growth stabilises itself through its action on signal transport. The significance of the dilution effect depends on the diffusion coefficient of the signal and on the growth rate of the tissue. In the cambium, the characteristic growth rate can be estimated around 2 10−6 s−1, based on data from Cuny et al. (2014). This means that the dilution effect is significant if the order of magnitude of the diffusion coefficient is 0.1 μm2 s−1 or less. In living roots of Arabidopsis thaliana, the diffusion coefficient of small molecules in the cell wall has been estimated at about 30 μm2 s−1 (Kramer et al. 2007). Growth-induced dilution is thus unlikely to play a significant role in the cambium. However, it can have an effect in faster growing tissues, like root meristems (Band et al. 2012). For a polarly transported signal, opposite orientations of the transporters led to radically opposite outcomes. Unlike many auxin transport models in other tissues, in which auxin is canalised away from its source, we proposed that, in the cambium, transporters confine auxin in the vicinity of the source as this was the only way to reach a steep and stationary concentration profile. This prediction of the XyDyS model could be assessed experimentally using PIN markers, as it has been already done in the shoot apical meristem (Reinhardt et al. 2003).

ii) The concentration profile was found to be informative enough to guide the zonation during the largest part of the growing season. This can be achieved through a modulation of the extent of the profile. For a signal diffusing in the apoplast, a plausible mechanism could be a tuning of the decay rate of the signal throughout the growing season. This mechanism has already been exemplified in animal morphogenesis (Wartlick and González-Gaitán 2011; Inomata et al. 2013). In plants, this tuning could be under the control of seasonal variations in day length, temperature, or water status. If the signal is polarly transported, the modulation of the extent of the profile would most probably involve variations in the quantity of carriers. This could be managed via the activation of genes coding for the carriers. In the specific case of auxin, Schrader et al. (2003) reported that PAT genes exhibit differential levels of expression during earlywood and latewood formation. It can be hypothesised that the expression of PAT genes responds to changes in environmental conditions (e.g. day length, temperature, water stress, mechanical stresses). How these external factors are spatially mediated along the cell file remains, however, an open question. If this mediation involves other signalling molecules transported in the tissue, then this upstream signalling raises the same problem as for the morphogenetic signal and may be addressed within a conceptual framework similar to the one we presented in this article. But then, more complex models will be required, since the transport capacities of the signals would depend on the spatial distribution of the signals themselves.

iii) Despite the above results, we show that the morphogenetic-gradient hypothesis does not account for the tree-ring structure. Positional information as provided by a morphogenetic gradient was found insufficient to regulate final cell sizes. The gradient guides zonation independently from the growth of each individual cell. In addition, this guidance mechanism produces an inhomogeneous cellular structure, which is not observed in real tissue. The question of how cell size is controlled in plant morphogenesis is puzzling and recurrent in the literature (Beemster and Baskin 1998; Harashima and Schnittger 2010; Powell and Lenhard 2012; Sablowski and Dornelas 2014). Concerning trees and wood, the tree-ring structure is strikingly stable compared to other tree characteristics under environmental control (Balducci et al. 2016). From our results, it clearly appears that a morphogenetic gradient does not offer a satisfactory answer, strongly suggesting the existence of an additional regulatory mechanism.

Wood formation involves numerous biochemical signals, with complex interactions (Růžička et al. 2015). Therefore, it can be hypothesised that at least two signals act together to control the development of wood-forming tissue. This idea is supported by several experimental findings. For instance, it has been demonstrated by Etchells et al. (2013) that TDIF must act in concert with a second signal for guiding the establishment of vascular organisation. That signal is identified as the receptor kinase ERECTA. In roots, a feedback loop between auxin and cytokinin has been found to specify vascular pattern (Bishopp et al. 2011). However, these two works did not directly address cell size control. Besides, water and carbohydrates also play a role, possibly in interaction with biochemical signals. They both have fluctuating statuses over a growing season. However, these two factors can be, at least partly, modelled as diffusive signals contributing to set the cell growth rates. This again calls for considering additional signals in our model.

Fully assessing whether multiple signals could provide a positional control that would actually account for final cell sizes requires much further investigations and should be the matter of another paper. However, we explored a single, minimal two-signal model (see S1 Text). It proved out that a two-signal model can indeed reproduce the global variation in cell diameters through a growing season, but that it does not solve the size-oscillation problem, therefore remaining unrealistic. Actually, these oscillations cannot be fully smoothed out unless the morphogenetic-gradient hypothesis itself is amended. This hypothesis is essentially a spatial perspective, in which developmental zones are specified by positional controls. It could thus be partially substituted for a cell-autonomous perspective, in which the trajectory of a cell is specified just before it leaves the meristem (Beemster and Baskin 1998). In such a model, only the division zone would be spatially specified by a signal concentration profile. After leaving this zone, each cell would be endowed with a certain capacity for enlargement. The endowment could take the form of a quantity of some other signals. Attributing such a pre-eminence to the cambial zone would also be in line with the hierarchical control proposed by Vaganov et al. (2011). But this hypothesis remains to be tested through appropriate dynamical modelling.

Although our modelling approach could not explain all the characteristic patterns observed in xylogenesis, it shed light on the complex dynamics of wood-forming tissue. The cambium is not a passive sink, whose activity is merely driven by the state of a source, that is by the amount of the morphogenetic signal (auxin, TDIF) at the boundary of the cambium. Instead, the cambial tissue responds to such signals in a non-trivial way. In particular, the response is mediated by how the signal is transported across the tissue. Transport within a developing tissue involves processes beyond simple thermal diffusion (Howard et al. 2011). Consequently, the shape of a morphogen gradient undergoes temporal changes as development proceeds (Kutejova et al. 2009). We highlighted that feedback loops and transient states, emerging from the dynamic interplay between growth and signal transport, are critical in the response of the tissue. For instance, the rapid increase in the number of cambial cells at the beginning of the growing season could be explained by a transient state during the initial establishment of the morphogen gradient. This is due to a fast relative change in the size of the tissue. After the transient state, we proposed that changes in the zonation are controlled by either the degradation rate or the density of carriers. In both cases, the control is internal to the tissue. These results support the idea that the cambium has a complex intrinsic dynamics, which is, to a large extent, autonomous from the environment and from the other organs of the tree.

However, autonomy has its limits. The onset of cambial activity is likely to be triggered by environmental factors such as temperature (Begum et al. 2012), but also by tree-scale events like possibly the reestablishments of the sapflow (Turcotte et al. 2009). Similarly, we could simulate how the growth speed reaches a steady value, but not the gradual decline of growth until final stop at the end of the growing season. Cessation of growth before winter is probably based on complex mechanisms involving responses to external cues, e.g. day length (Baba et al. 2011) and temperature (Begum et al. 2016). Investigating these environmental effects would require more modelling efforts, integrating xylogenesis modelling into forest ecophysiological modelling (e.g. Deckmyn et al. 2008; Guillemot et al. 2015). In any case, models with a cellular structure and an explicit spatial-temporal description, like XyDyS, are promising candidates to make progress in that direction, since they are able to integrate influences of external factors on each cell along its differentiation trajectory together with the intrinsic morphogenetical dynamics of cambial meristematic activity. They will give validated processes to infer rules of spatial zonations in current approaches of cambial activity modelling (Hölttä et al. 2010; Drew and Downes 2015).