Skip to main content

Advertisement

SpringerLink
Log in

CPFD simulation of a dual fluidized bed cold flow model

  • Original Article
  • Published:
Biomass Conversion and Biorefinery Aims and scope Submit manuscript

Abstract

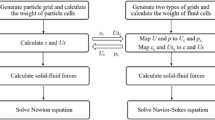
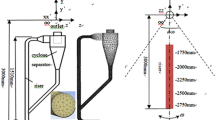
The present work was carried out to simulate a cold flow model of a biomass gasification plant. For the simulation, a Eulerian-Lagrangian approach, more specifically the multi-phase particle in cell (MP-PIC) method, was used to simulate particles with a defined particle size distribution. Therefore, Barracuda VR, a software tool with an implemented MP-PIC method specifically designed for computational particle fluid dynamics simulations, was the software of choice. The simulation results were verified with data from previous experiments conducted on a physical cold flow model. The cold flow model was operated with air and bronze particles. The simulations were conducted with different drag laws: an energy-minimization multi-scale (EMMS) approach, a blended Wen-Yu and Ergun drag law, and a drag law of Ganser. The fluid dynamic behavior depends heavily on the particles’ properties like the particle size distribution. Furthermore, a focus was placed on the normal particle stress (PS value variation), which is significant in close-packed regions, and the loop seals’ fluidization rate was varied to influence the particle circulation rate. The settings of the simulation were optimized, flooding behavior did not occur in advanced simulations, and the simulations reached a stable steady state behavior. The Ganser drag law combined with an adjusted PS value with (PS = 30 Pa) or without (PS = 50 Pa) increased loop seal fluidization rates provided the best simulation results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the corresponding author, A. Lunzer, upon reasonable request.

Abbreviations

AR:

air reactor, combustion reactor

BB:

bubbling bed

BCs:

boundary conditions

CFB:

circulating fluidized bed

CFD:

computational fluid dynamics

CPFD:

computational particle fluid dynamics

DFB:

dual fluidized bed

e.g.:

exempli gratia

EMMS:

energy-minimization multi-scale (EMMS drag model)

Eq.:

equation

Fig.:

figure

FR:

fuel reactor, gasification reactor

ILS:

inner loop seal

LES:

large eddy simulation

LLS:

lower loop seal

MP-PIC:

multi-phase particle in cell

PSD:

particle size distribution

SEP:

separator

ULS:

upper loop seal

WYE:

Wen-Yu and Ergun (WYE drag model)

a p :

particle acceleration (\( \raisebox{1ex}{$\mathrm{m}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{s}}^2$}\right. \))

D :

drag function (\( \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{s}$}\right. \))

F :

interphase momentum transfer function (N/m3)

\( \boldsymbol{g} \) :

gravitational acceleration (\( \raisebox{1ex}{$\mathrm{m}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{s}}^2$}\right. \))

p :

pressure (Pa)

P S :

constant to calculate τp (Pa)

t :

time (s)

u f :

fluid velocity (m/s)

u mf :

minimum fluidization velocity (m/s)

u p :

particle velocity

(m/s)

\( {\overline{\boldsymbol{u}}}_{\mathrm{p}} \) :

particle mean velocity (m/s)

x i :

spatial variable (m)

α :

constant to calculate τp

β :

constant to calculate τp

ε cp :

close-pack particle volume fraction

ε f :

fluid volume fraction

ε p :

particle volume fraction

δ ij :

Kronecker delta

m p :

particle mass (kg)

μ :

viscosity (\( \raisebox{1ex}{$\mathrm{kg}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{m}\times \mathrm{s}$}\right. \))

∇:

nabla operator (\( \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{m}$}\right. \))

ρ f :

fluid density (\( \raisebox{1ex}{$\mathrm{kg}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{m}}^3$}\right. \))

τ D :

damping time due to inelastic particle collisions (s)

τ f :

fluid stress tensor (\( \raisebox{1ex}{$\mathrm{N}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{m}}^2$}\right. \))

τ p :

particle normal stress (\( \raisebox{1ex}{$\mathrm{N}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{m}}^2$}\right. \))

References

  1. Schmid J (2014) Development of a novel dual fluidized bed gasification system. TU Wien

  2. Kraft S, Kirnbauer F, Hofbauer H (2017) CPFD simulations of an industrial-sized dual fluidized bed steam gasification system of biomass with 8 MW fuel input. Appl Energy 190:408–420. https://doi.org/10.1016/j.apenergy.2016.12.113

    Article  Google Scholar 

  3. Kuba M, Kraft S, Kirnbauer F, Maierhans F, Hofbauer H (2018) Influence of controlled handling of solid inorganic materials and design changes on the product gas quality in dual fluid bed gasification of woody biomass. Appl Energy 210:230–240

    Article  Google Scholar 

  4. Fotovat F, Abbasi A, Spiteri RJ, de Lasa H, Chaouki J (2015) A CPFD model for a bubbly biomass-sand fluidized bed. Powder Technol 275:39–50. https://doi.org/10.1016/j.powtec.2015.01.005

    Article  Google Scholar 

  5. Liang Y, Zhang Y, Li T, Lu C (2014) A critical validation study on CPFD model in simulating gas-solid bubbling fluidized beds. Powder Technol 263:121–134. https://doi.org/10.1016/j.powtec.2014.05.003

    Article  Google Scholar 

  6. Weber JM, Layfield KJ, Van Essendelft DT, Mei JS (2013) Fluid bed characterization using electrical capacitance volume tomography (ECVT), compared to CPFD software’s barracuda. Powder Technol 250:138–146. https://doi.org/10.1016/j.powtec.2013.10.005

    Article  Google Scholar 

  7. Zhang L, Wang Z, Wang Q, Qin H, Xu X (2016) Simulation of oil shale semi-coke particle cold transportation in a spouted bed using CPFD method. Powder Technol 301:360–368. https://doi.org/10.1016/j.powtec.2016.06.012

    Article  Google Scholar 

  8. Shi X, Sun R, Lan X, Liu F, Zhang Y, Gao J (2015) CPFD simulation of solids residence time and back-mixing in CFB risers. Powder Technol 271:16–25. https://doi.org/10.1016/j.powtec.2014.11.011

    Article  Google Scholar 

  9. Shi X, Wu Y, Lan X, Liu F, Gao J (2015) Effects of the riser exit geometries on the hydrodynamics and solids back-mixing in CFB risers: 3D simulation using CPFD approach. Powder Technol 284:130–142. https://doi.org/10.1016/j.powtec.2015.06.049

    Article  Google Scholar 

  10. Rodrigues SS, Forret A, Montjovet F, Lance M, Gauthier T (2015) CFD modeling of riser with group B particles. Powder Technol 283:519–529. https://doi.org/10.1016/j.powtec.2015.05.020

    Article  Google Scholar 

  11. Wang Q, Niemi T, Peltola J, Kallio S, Yang H, Lu J, Wei L (2015) Particle size distribution in CPFD modeling of gas-solid flows in a CFB riser. Particuology. 21:107–117. https://doi.org/10.1016/j.partic.2014.06.009

    Article  Google Scholar 

  12. Shi X, Lan X, Liu F, Zhang Y, Gao J (2014) Effect of particle size distribution on hydrodynamics and solids back-mixing in CFB risers using CPFD simulation. Powder Technol 266:135–143. https://doi.org/10.1016/j.powtec.2014.06.025

    Article  Google Scholar 

  13. Chen C, Werther J, Heinrich S, Qi HY, Hartge EU (2013) CPFD simulation of circulating fluidized bed risers. Powder Technol 235:238–247. https://doi.org/10.1016/j.powtec.2012.10.014

    Article  Google Scholar 

  14. Clark S, Snider DM, Spenik J (2013) CO2 adsorption loop experiment with eulerian-lagrangian simulation. Powder Technol 242:100–107. https://doi.org/10.1016/j.powtec.2013.01.011

    Article  Google Scholar 

  15. Wang Q, Yang H, Wang P, Lu J, Liu Q, Zhang H, Wei L, Zhang M (2014) Application of CPFD method in the simulation of a circulating fluidized bed with a loop seal, part I-determination of modeling parameters. Powder Technol 253:814–821. https://doi.org/10.1016/j.powtec.2013.11.041

    Article  Google Scholar 

  16. Hamilton MA, Whitty KJ, Lighty JS (2016) Numerical simulation comparison of two reactor configurations for chemical looping combustion and chemical looping with oxygen uncoupling. J Energy Resour Technol 138:042213. https://doi.org/10.1115/1.4033108

    Article  Google Scholar 

  17. Adkins BD, Kapur N, Dudley T, Webb S, Blaser P (2017) Experimental validation of CFD hydrodynamic models for catalytic fast pyrolysis. Powder Technol 316:725–739. https://doi.org/10.1016/j.powtec.2016.11.060

    Article  Google Scholar 

  18. Ma Q, Lei F, Xu X, Xiao Y (2017) Three-dimensional full-loop simulation of a high-density CFB with standpipe aeration experiments. Powder Technol 320:574–585. https://doi.org/10.1016/j.powtec.2017.07.094

    Article  Google Scholar 

  19. Kraft S, Kirnbauer F, Hofbauer H (2017) Influence of drag laws on pressure and bed material recirculation rate in a cold flow model of an 8 MW dual fluidized bed system by means of CPFD. Particuology 36:70–81. https://doi.org/10.1016/j.partic.2017.04.009

    Article  Google Scholar 

  20. Snider DM, Clark SM, O’Rourke PJ (2011) Eulerian-Lagrangian method for three-dimensional thermal reacting flow with application to coal gasifiers. Chem Eng Sci 66:1285–1295. https://doi.org/10.1016/j.ces.2010.12.042

    Article  Google Scholar 

  21. O’Rourke PJ, Snider DM (2014) A new blended acceleration model for the particle contact forces induced by an interstitial fluid in dense particle/fluid flows. Powder Technol 256:39–51. https://doi.org/10.1016/j.powtec.2014.01.084

    Article  Google Scholar 

  22. Snider DM (2001) An incompressible three-dimensional multiphase particle-in-cell model for dense particle flows. J Comput Phys 170:523–549. https://doi.org/10.1006/jcph.2001.6747

    Article  Google Scholar 

  23. Andrews MJ, O’Rourke PJ (1996) The multiphase particle-in-cell (MP-PIC) method for dense particulate flows. Int J Multiphase Flow 22:379–402. https://doi.org/10.1016/0301-9322(95)00072-0

    Article  Google Scholar 

  24. Yang N, Wang W, Ge W, Wang L, Li J (2004) Simulation of heterogeneous structure in a circulating fluidized-bed riser by combining the two-fluid model with the EMMS approach. Ind Eng Chem Res 43:5548–5561. https://doi.org/10.1021/ie049773c

    Article  Google Scholar 

  25. Chhabra RP, Agarwal L, Sinha NK (1999) Drag on non-spherical particles: an evaluation of available methods. Powder Technol 101:288–295

    Article  Google Scholar 

  26. Wen CY YH Yu (1966). Mechanics of fluidization. In: chemical engineering Progress symposium series. Pp 100–111

  27. Martinovic D (2013) Kaltmodellversuche und MSR-Konzept einer Zweibett-Wirbelschicht-Vergasungsanlage. TU Wien

  28. Gidaspow D (1994) Multiphase flow and fluidization: continuum and kinetic theory descriptions. Academic press

  29. Ergun S (1952) Fluid flow through packed columns. Chem Eng Prog 48:89–94

    Google Scholar 

  30. CPFD Software LLC. (2018) Barracuda Virtual Reactor User Manual

  31. Kraft S (2017) Investigation of particle mixing in dual fluidized bed gasification systems by means of cold flow modelling and computational methods. TU Wien

  32. Bi HT, Grace JR (1995) Flow regime diagrams for gas-solid fluidization and upward transport. Int J Multiphase Flow 21:1229–1236. https://doi.org/10.1016/0301-9322(95)00037-X

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Verto Engineering GmbH, Franz-Josefs Kai 53/13, 1010, Vienna, Austria

    A. Lunzer

  2. Institute of Chemical, Environmental and Bioscience Engineering, TU Wien, Getreidemarkt 9/166, 1060, Vienna, Austria

    S. Kraft, S. Müller & H. Hofbauer

  3. Bioenergy 2020+ GmbH, Wiener Strasse, 49, 7540, Güssing, Austria

    S. Kraft

Authors
  1. A. Lunzer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Kraft
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. Müller
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. H. Hofbauer
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Lunzer.

Ethics declarations

Conflict of interest

Not applicable.

Code availability

Not applicable

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lunzer, A., Kraft, S., Müller, S. et al. CPFD simulation of a dual fluidized bed cold flow model. Biomass Conv. Bioref. 11, 189–203 (2021). https://doi.org/10.1007/s13399-020-01229-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13399-020-01229-4

Keywords

Search

Navigation