Thermal uncertainty analysis of a single particle model for a Lithium-Ion cell

Abstract

In recent years, the sustained increase in the worldwide demand for lithium batteries goes side by side with the need for reliable methods to assess battery performance. Of particular importance is assessing Lithium-Ion cell’s thermal behavior given its role on hazard and aging of batteries. An essential task towards developing battery management systems is the estimation of physical parameters and their uncertainties in terms of both models and observations. Consequently, this paper analyzes the uncertainty in a thermal single particle model for a lithium-ion cell. In the first part of the manuscript, we explore the model adequacy by analyzing the forward and backward uncertainty propagation in the model in terms of diffusion coefficients, reaction rate constants, and observations of cell voltage. In the second part of the manuscript, we infer the cell’s reversible heat given the energy balance equation and the cell’s temperature observations. We argue that the methods proposed here may be extended to analyze other more general lithium-ion models.

1 Introduction

The worldwide demand for Lithium-Ion batteries has continuously increased during the last decades. The development of models to simulate battery behavior has gone side by side. Broadly speaking, first principle models of batteries are based on multiphysics and are fundamental from a theoretical point of view [1,2,3]. Unfortunately, these models are complex and computationally expensive to simulate, which is a limitation in applications, i.e., design and analysis, where the intense simulation of battery behavior under multiple regimes is required. Because of these arguments, the worldwide community has developed reduced-order models. These types of models, many of them phenomenological, reproduce battery dynamics successfully.

Computer models arising from the discretization of battery models will be useful as long as there is confidence in their predictions, mainly to assist decision making [4]. Since reduced-order models are typically easier to implement and faster to simulate, quantitative methods are required to evaluate reduced-order models’ ability to predict quantities of interest as input parameters vary across regimes. An appropriate approach to address this question is the forward and backward uncertainty propagation analysis. In this regard, it is important to analyze the model adequacy to predict the lithium-ion cell thermal behavior given its role on battery performance, safety, aging, wear and tear.

To address these questions, in this paper, we consider a thermal single-particle model (TSPM), studied by Guo et al. [5], that assumes non-constant temperature along time and couples lithium concentration and thermal balance equations. It is a reduced-order model whose numerical simulation cost allows it to combine with Monte Carlo simulations.

First, we analyze the forward uncertainty propagation of the transport and kinetic coefficients—i.e., its identifiability—through global sensitivity analysis. To accomplish this task, we analyze each coefficient’s contributions to the likelihood’s variance. We define the likelihood as the conditional probability of voltage observations given these model coefficients in the present setting. We find that four parameters (the diffusion coefficient and the reaction rate activation energies, of both electrodes) with the same scale are identifiable from voltage measurements.

On the other hand, to carry out backward uncertainty analysis, we elicit prior distribution models for the activation energy parameters and use them, with the likelihood, to analyze the conditional probability of these coefficients given voltage observations. Of note, voltage observations are easier to obtain compared to temperature observations, see [6]. We apply this strategy to Guo’s reduced-order model to find a conditional probability of the activation energy parameters given voltage observations. We remark that this is not a trivial task since “...the task of parameter identification is challenging. [...] many parameters are weakly identifiable from current and voltage measurements....", see [7]. In this context, we must highlight that we make inferences with a computer model whose solutions mimic the continuous model solutions with a specific order of error in practice. In this paper, we use the estimate introduced in [8] for the solution of the inverse problem in terms of the computer model error. Based on voltage observations, this estimation provides evidence to decide on the grid thickness used to solve the computer model.

As a second line of evidence of the TSPM’s predictive capacity, we infer the reversible heat of the lithium-ion cell using the energy balance equation and temperature observations during a discharge cycle. A central part of our method is estimating the temperature derivative solving a linear inverse problem with the Bayesian paradigm. We use spatial statistics methods to propose a prior model of the temperature derivative, which we regard as a distributed parameter, using a Gaussian Markov random field. We accomplish this task in two steps. First, we pose a uniformly spaced prior model, and secondly, we subsample a central subinterval where the pointwise variance is smaller. This strategy allows us to reduce the variance of the posterior model and reduce the number of degrees of freedom. This approach is based on well known model reduction methods, see for example Spantini et al. [9] or Bui et al. [10].

Related work There are many research efforts aimed at analyzing cycling performance of lithium ion batteries taking into account thermal effects [5, 11,12,13,14]. Marcicki et al. [15] considered a lumped energy balance equation and Kalman filtering to estimate heat generation during cycling for Li-ion cells. Bizeray thesis [16] contributes towards state and parameter estimation of thermal-electrochemical lithium-ion battery models, noteworthy are the performance estimation analyses based on extended Kalman filtering. Tagade et al. [17] carried out a synthetic analysis of experimental design and bayesian calibration of an electrochemical termal model. Chen et al. [18] proposed a 3D model aimed at exploring battery thermal behavior taking into account the battery shape. Raijmakers et al. [6] provided a review on heat generation principles, as well as methods and challenges in battery temperature measurement methods.

Regarding sensitivity analysis, [19,20,21,22] investigate global sensitivity analysis of electrochemical models of Li-ion cells including thermal effects.

Likewise, there are inverse analysis electrochemical systems defined by Li-ion batteries, see [23,24,25].

Contributions and limitations We explore the adequacy of a thermal single particle model for a Lithium-Ion cell. Our forward uncertainty propagation analysis reveals a relation between forward uncertainty propagation and practical parameter identifiability when we consider the likelihood function as a quantity of interest (QoI). Moreover, in the backward uncertainty analysis we find a probability distribution for these parameters. On the other hand, we estimate the reversible heat using this model for a lithium-ion cell with quantified uncertainty. We use methods of spatial statistics to elicit a prior statistical model for the derivative of the temperature. The corresponding inference process accounts for dimension reduction exploiting the fact that the conditional probability of the temperature derivative is a Gaussian distribution. We point out that our analysis can be applied to other models for lithium-ion cells. We show the importance of prior model elicitation to estimate the reversible heat.

The remainder of this manuscript is organized as follows: Sect. 2 presents the analyzed model and the theoretical analysis tools. Section 3 makes a discussion of our results. Finally, Sect. 4 summarizes our findings and their generality.

2 Methods

For the sake of making this paper self-contained, in this section, we gather the theoretical methods used in our in silico analysis.

2.1 Thermal Li-ion single cell model

We consider the thermal single particle model for a Lithium-Ion cell described by Guo et al. [5], which reads as follows. Assuming each electrode can be represented by a single intercalation spherical particle, the mass balance of lithium ions in an intercalation particle of electrode active material is described by Fick’s second law in a spherical coordinate system

$$\begin{aligned} \frac{\partial c_{\textrm{s}, \textrm{j}}}{\partial t}=\frac{D_{\textrm{s}, \textrm{j}}}{r^{2}} \frac{\partial }{\partial r}\left( r^{2} \frac{\partial c_{\textrm{s}, \textrm{j}}}{\partial r}\right) , \end{aligned}$$

(1)

where $c_{\textrm{s}, \textrm{j}}$ is the concentration of lithium ions in the intercalation particle, t is time, r is the radius direction coordinate, $D_{\textrm{s}, \textrm{j}}$ is the solid phase diffusion coefficient, which is a function of temperature, and the subscript $\mathrm{j = p/n}$ represents the positive/negative electrode. We also have the initial conditions

$$\begin{aligned} c_{\textrm{s}, \textrm{j}}(t=0)=c_{\textrm{s}, \textrm{ini}, \textrm{j}}, \end{aligned}$$

(2)

and the boundary conditions

$$\begin{aligned} \begin{aligned} \left( D_{\textrm{s}, \textrm{j}} \frac{\partial c_{\textrm{s}, \textrm{j}}}{\partial r}\right) _{r=0}&=0,\\ \left( D_{\textrm{s}, \textrm{j}} \frac{\partial c_{\textrm{s}, \textrm{j}}}{\partial r}\right) _{r=R_{\textrm{j}}}&=-J_{\textrm{j}}, \end{aligned} \end{aligned}$$

(3)

where $r=R_\textrm{j}$ is the particle radius, and

$$\begin{aligned} J_{\textrm{p}}=\frac{I}{F S_{\textrm{p}}}, \quad J_{\textrm{n}}=-\frac{I}{F S_{\textrm{n}}}, \end{aligned}$$

with I the total current, $F=96{,}487$ C/mol the Faraday constant and $S_\textrm{j}$ the total electroactive surface area of electrode $\textrm{j}$.

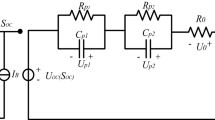
Assuming that the spatial temperature distribution in the cell can be neglected, the cell temperature T is a function of time only, satisfying

$$\begin{aligned} M C_\textrm{p} \frac{\textrm{d} T}{\textrm{d} t}=I T\left[ \frac{\partial U_{\textrm{p}}}{\partial T}\left( x_{\textrm{p}, \textrm{surf}}\right) -\frac{\partial U_{\textrm{n}}}{\partial T}\left( x_{\textrm{n}, \textrm{surf}}\right) \right] +I\left( \eta _{\textrm{p}}-\eta _{\textrm{n}}+I R_{\textrm{cell}}\right) -q. \end{aligned}$$

(4)

Here M and $C_\textrm{p}$ are the mass and the specific heat capacity of cell, respectively. In addition, $U_{\textrm{j}}$ is the Open Circuit Potencial (OCP) and $x_{\textrm{j}, \textrm{surf }}=\frac{\left. c_{\textrm{s}, \textrm{j}}\right| _{r=R_{\textrm{j}}}}{c_{\textrm{s}, \textrm{j}, \max }}$ is the State of Charge (SoC). The overpotential $\eta _{\textrm{j}}$ is defined as

$$\begin{aligned} \eta _{\textrm{j}}=\frac{2 R T}{F} \ln \left( \frac{\sqrt{m_{\textrm{j}}^{2}+4}+m_{\textrm{j}}}{2}\right) , \end{aligned}$$

where

$$\begin{aligned} m_{\textrm{j}}=\frac{I}{F k_{\textrm{j}} S_{\textrm{j}} c_{\textrm{s}, \textrm{j}, \max } c_{\textrm{e}}^{0.5}\left( 1-x_{\textrm{j}, \textrm{surf}}\right) ^{0.5} x_{\textrm{j} \textrm{surf}}^{0.5}}, \end{aligned}$$

being $k_{\textrm{j}}$ the reaction rate constant and $c_{\textrm{e}}$ the (assumed constant in this model) electrolyte concentration in solution phase. Finally, $R_{\textrm{cell}}$ is the electrolyte resistance and q is the rate of heat transfer between cell and surroundings.

The initial cell temperature is assumed to be ambient temperature

$$\begin{aligned} \left. T\right| _{t=0}=T_{\textrm{amb}}. \end{aligned}$$

(5)

In this context, it is possible to explicit the cell voltage $V_\textrm{cell}$ as

$$\begin{aligned} V_{\textrm{ cell }}= U_{\textrm{p}}\left( x_{\textrm{p}, \textrm{surf}}\right) -U_{\textrm{n}}\left( x_{\textrm{n}, \textrm{surf}}\right) +\eta _{\textrm{p}}-\eta _{\textrm{n}} +I R_{\textrm{cell}}. \end{aligned}$$

(6)

The transport and kinetic parameters involved in the model equations are functions of temperature. The solid phase diffusion coefficients $D_{\textrm{s}, \textrm{j}}$ and the reaction rate constants $k_{\textrm{j}}$ depend on the temperature through Arrhenius’ correlation

$$\begin{aligned} \begin{array}{c} {D_{\textrm{s}, \textrm{j}}(T)=D_{\textrm{s}, \textrm{j}, \textrm{ref}} \exp \left[ \frac{E_\mathrm{a_{di,j}}}{R}\left( \frac{1}{T}-\frac{1}{T_{\textrm{ref}}}\right) \right] }, \\ {k_{\textrm{j}}(T)=k_{\textrm{j}, \textrm{ref}} \exp \left[ \frac{E_\mathrm{a_{re,j}}}{R}\left( \frac{1}{T}-\frac{1}{T_{\textrm{ref}}}\right) \right] }.\end{array} \end{aligned}$$

where $E_\mathrm{a_{di,j}}$ and $E_\mathrm{a_{re,j}}$ are the diffusion coefficient activation energy and the reaction rate activation energy, respectively, of electrode j. Of note, the dependence of coefficients $D_{\textrm{s}, \textrm{j}}$ on temperature implies that Eqs. (1) and (4) are coupled.

2.2 Computer model

Broadly speaking, battery model analysis is concerned with studying the solution of model (1)–(6) under different parameter regimes. Let us denote

$$\begin{aligned} \theta =(E_\mathrm{a_{di,p}},E_\mathrm{a_{di,n}},E_\mathrm{a_{re,p}},E_\mathrm{a_{re,n}}), \end{aligned}$$

(7)

the activation energy parameter vector and let $V_\textrm{cell}(t)$ be the cell voltage at time t. Equations (1)–(6) define a forward mapping ${\mathcal {M}}$ from these model parameters to cell voltage

$$\begin{aligned} {\mathcal {M}}:\theta \longrightarrow V_\textrm{cell}. \end{aligned}$$

The forward mapping $V_\textrm{cell}={\mathcal {M}}(\theta )$ has no analytical expression. Thus, to explore problem (1)–(6), we rely on a computer model $V^{h}_\textrm{cell}={\mathcal {M}}^{h}(\theta ) \in {\mathbb {R}}^{N}$, where h accounts for a discretization size and N is the dimension of the corresponding finite dimensional space. In this paper, we propose ${\mathcal {M}}^{h}$ implementing second-order centered finite differences in space and Crank-Nicolson scheme to march in time to deal with equation (1), as well as a two stage Runge-Kutta second-order method (namely, Heun’s method) to approximate the solution of thermal equilibrium Eq. (4).

Practical validation of a computer model is necessary if we are to use model ${\mathcal {M}}^{h}$ as a surrogate of model ${\mathcal {M}}$ to explore backward and forward uncertainty propagation. In the absence of an analytical expression of $V_\textrm{cell}$, in order to provide a numerical convergence rate of the computer model, we compute

$$\begin{aligned} p_{h}\simeq \log _{2}\left( \frac{\left\| V^{4 h}_\textrm{cell}-V^{2 h}_\textrm{cell}\right\| _{\infty }}{\left\| V^{2 h}_\textrm{cell}-V^{h}_\textrm{cell}\right\| _{\infty }}\right) , \end{aligned}$$

where the norms $||\cdot ||_{\infty }$ are computed on the corresponding coarser mesh. Of note $p_{h} \approx 1.99$, for $h=2^{-j}$ for $j=2,3,4,\ldots$ This value of $p_h$ suggests a quadratic order of convergence.

2.3 Forward and backward uncertainty analysis

Let us denote by $v=(v_{i})_{i=1}^{N}$ the voltage observations at times $t=(t_{i})_{i=1}^{N}$. We shall assume $v_{i}=V_\textrm{cell}(t_{i};\theta )+\eta _{i}$. Namely, we assume that a voltage observation $v_{i}$ is the model prediction $V_\textrm{cell}(t_{i};\theta )$ for a given set of parameters $\theta$ with additive noise, e.g. $\eta _{i}\sim {\mathcal {N}}(0,\sigma ^{2})$ for $i=1,\ldots ,N$. Then, the conditional probability of $v_{i}$ given $\theta$ is $v_{i}|\theta \sim {\mathcal {N}}(V_\textrm{cell}(t_{i};\theta ),\sigma ^{2})$. In the synthetic examples shown in Sect. 3, the standard deviation $\sigma$ of the noise is set such that the signal to noise ratio (SNR) satisfies

$$\begin{aligned} \frac{\max (V_\textrm{cell})}{\sigma } = 10^{2} \end{aligned}$$

to mimic the precision of instruments used to measure voltage. We have made the hypothesis that there is no interference, see Johnson [26]. If we assume observations are independent then we obtain a model of the conditional probability of v given $\theta$

$$\begin{aligned} \pi _{V|\Theta }(v|\theta )=\prod _{i=1}^{N}\frac{1}{\sqrt{2\pi \sigma ^{2}}}\exp \left( -\frac{1}{2\sigma ^2}(v_{i}-V_\textrm{cell}(t_{i};\theta ))^2\right) . \end{aligned}$$

(8)

In Sect. 3 we analyze the uncertainty in the forward model $V_\textrm{cell}={\mathcal {M}}(\theta )$ through global sensitivity analysis. To accomplish this task, we explore the practical parameter identifiability by taking the likelihood (8) as a quantity of interest in the Sobol sensitivity analysis.

According to Salltelli et al. [27], the first order Sobol sensitivity analysis for a quantity of interest $Y=Y(\theta )$ is defined by

$$\begin{aligned} S_{i}=\frac{\textrm{var}_{\theta _{i}}\left( {\mathbb {E}}_{{\theta }_{\sim i}}\left( Y | \theta _{i}\right) \right) }{\textrm{var}(Y)}, \end{aligned}$$

(9)

where $\textrm{var}(Y)$ is the variance of the quantity of interest Y, $\textrm{var}_{\theta _{i}}(\cdot )$ denotes the variance of argument $(\cdot )$ taken over $\theta _i$, and ${\mathbb {E}}_{{\theta }_{\sim i}}(\cdot )$ denotes the expectation of argument $(\cdot )$ taken over all factors but $\theta _i$. We use (9) to explore the contribution of the variance in each model parameter to the variance in the likelihood (8). In Sect. 3 we argue that all activation energy parameters $\theta$ are practically identifiable given voltage observations.

On the other hand, in the backward uncertainty analysis, we care about the uncertainty in the parameters $\theta$ given observations of the voltage. Thus, we shall use the Bayesian paradigm to model the conditional probability of the vector of model parameters $\theta$ given a vector of observations $v=(v_1,\ldots ,v_N)^{T}$. The prior model

$$\begin{aligned} \pi _{\Theta }(\theta ) \end{aligned}$$

(10)

codes into a probability density function available information about the parameters that is independent from the voltage observations. If $\pi _{\Theta }(\theta )$ is a prior distribution of the model parameters, then the uncertainty of the model parameters given observations of the voltage is given by the posterior distribution

$$\begin{aligned} \pi _{\Theta |V}(\theta |v)=\frac{\pi _{V|\Theta }(\theta |v)\pi _{\Theta }(\theta )}{Z(v)}, \end{aligned}$$

(11)

where Z(v) is the normalization constant, often unknown.

There are no analytical methods to explore the posterior distribution (11), e.g., to obtain its estimators, for example, the maximum a posteriori $\theta _{MAP}=\max _{\theta }\pi _{\Theta |V}(\theta |v)$, the posterior conditional mean $\theta _{CM}={\mathbb {E}}[\pi _{\Theta |V}(\theta |v)]$ or posterior median $\theta _\textrm{median}$. Thus, in Sect. 3 we shall use a stochastic collocation method called Markov Chain Monte Carlo (MCMC) to approximate numerically the posterior distribution (11).

2.4 Elicitation of the prior distribution for the activation energy parameters

To elicit a prior distribution (10) we shall assume $E_\mathrm{a_{di,j}}, E_\mathrm{a_{re,j}}\in [0,a \times 10^5]$, j=p/n. We set $a=2$ for $E_\mathrm{a_{di,p}}$ and $a=1$ for the rest of the activation energy parameters. Also, we use the fact that the parameter correlation structure is implicitly set into the forward model $V_\textrm{cell}={\mathcal {M}}(\theta )$ to pose the prior model as the product of a prior model for each parameter. Consequently, we model $E_\mathrm{a_{di,j}}/(a \times 10^5), E_\mathrm{a_{re,j}}/(a \times 10^5)~\sim Beta(\alpha ,\beta )$, where instrumental parameters $\alpha ,\beta$ are chosen following ${\mathbb {E}}[\log (\theta _{i})]=\psi (\alpha )-\psi (\alpha +\beta )$, $\textrm{var}(\log (\theta _{i}))=\psi _1(\alpha )-\psi _1(\alpha +\beta )$, being $\psi$ and $\psi _1$ are the first and second logarithmic derivatives of the Gamma function.

We remark that the Beta distribution is the maximum entropy distribution with support on [0, 1] that arises (see Singh et al. [28]) from requiring a probability density function $f=f_{\theta _i}(\theta _i)$ to satisfy

$$\begin{aligned} \int _{0}^{1} f_{\theta _i}(\theta _i) \textrm{d} \theta _i=1, \\ \int _{0}^{1} \ln \theta _i f_{\theta _i}(\theta _i) \textrm{d} \theta _i={\mathbb {E}}[\ln \theta _i], \end{aligned}$$

and

$$\begin{aligned} \int _{0}^{1} \ln (1-\theta _i) f_{\theta _i}(\theta _i) \textrm{d} \theta _i={\mathbb {E}}[\ln (1-\theta _i)], \end{aligned}$$

for $i=1, 2, 3, 4$. We set the instrumental parameters $\alpha =\beta =1.1$. Then we model the joint prior probability density (10) as the product

$$\begin{aligned} \pi _{\Theta }(\theta )= f_{E_\mathrm{a_{di,p}}}(E_\mathrm{a_{di,p}}/(2 \times 10^5))\times f_{E_\mathrm{a_{di,n}}}(E_\mathrm{a_{di,n}}/10^5)\times f_{E_\mathrm{a_{re,p}}}(E_\mathrm{a_{re,p}}/10^5)\times f_{E_\mathrm{a_{re,n}}}(E_\mathrm{a_{re,n}}/10^5). \end{aligned}$$

2.5 Estimation of the reversible heat

2.5.1 Bayesian approach

We shall use the equation of energy balance (4) to estimate the reversible heat given temperature observations $T(t_{i})$ at times $t_i$ for $i=1,\ldots ,m$. Following the notation of Marcicki [15], we assume the irreversible part of the generated heat to be $q_\textrm{irr}=I\left( \eta _{\textrm{p}}-\eta _{\textrm{n}}+I R_{\textrm{cell}}\right)$, while Newton’s law of cooling holds for the heat rejected to the environment $q_\infty =h \left( T-T_{\text{ amb }}\right)$. Furthermore, we shall assume that the cell mass M and the cell specific heat capacity $C_\textrm{p}$ are known. Consequently, if an approximation of the temperature derivative $\frac{\textrm{d}T}{\textrm{d}t}$ is available, then we can use the energy balance (4) to estimate the reversible heat $q_\textrm{rev}$ by

$$\begin{aligned} q_\textrm{rev}=M C_\textrm{p} \frac{\textrm{d}T}{\textrm{d}t}-q_\textrm{irr}-q_\infty . \end{aligned}$$

(12)

In order to use Eq. (12), we propose a Bayesian approach to estimate the temperature numerical derivative given noisy observations of T. If we regard numerical differentiation as an inverse problem, then the forward problem is a convolution with a Heaviside function H

$$\begin{aligned} T(t_{i})=\int _{{\mathbb {R}}}H(t_{i}-s)f(s)\textrm{d}s+\xi _{i}, \quad \xi _{i}\sim {\mathcal {N}}\left( 0,\gamma _{T}^{2}\right) , \end{aligned}$$

(13)

where f is the derivative of T in the zero noise limit and $\gamma _{T}^{2}$ is the noise variance. In the results presented in Sect. 3 we set the signal to noise ratio

$$\begin{aligned} \textrm{SNR}=\frac{\max T}{\gamma _{T}}=10^{2}. \end{aligned}$$

We shall use Eq. (13) to pose both, a computer model to solve the direct problem and a likelihood model. We discretize the integral in Eq. (13) using the composite medium point rule obtaining

$$\begin{aligned} T_i\doteq T(t_i)-T_{\textrm{amb}}=\int _{0}^{t_{i}}f(s)\textrm{d}s+\xi _{i}\approx \sum _{j=1}^{i}\Delta sf(s_j)+\xi _{i},\quad i=1,\ldots ,m, \end{aligned}$$

(14)

where we have assumed uniform timing in the observations $t_i=i\Delta s$ for $i=0,\ldots ,m$ and $s_j=\frac{1}{2}(t_{j-1}+t_{j})$ for $j=1,\ldots ,m$. Denoting by $T=(T_i)_{i=1}^{m}, f=\left( f(s_i)\right) _{i=1}^{m}$ and $\xi =(\xi _i)_{i=1}^{m}$, the discretized inverse problem (14) can be writen as

$$\begin{aligned} T=Af+\xi , \end{aligned}$$

(15)

where $A=(a_{ij})_{i,j=1}^{m}$ is the lower triangular matrix defined by

$$\begin{aligned} a_{ij} = {\left\{ \begin{array}{ll} \Delta s&{}\text {if}\;i\ge j,\\ 0&{}\text {other case.} \end{array}\right. } \end{aligned}$$

Assuming temperature observations are independent, the likelihood is given by the conditional probability

$$\begin{aligned} T|f\sim {\mathcal {N}}(Af,\Gamma _{obs}), \end{aligned}$$

(16)

where $\Gamma _{obs}=\gamma _{T}^{2}I_{m}$ and $I_{m}\in {\mathbb {R}}^{m\times m}$ are the covariance and identity matrices respectively.

We shall solve the inverse problem in two stages. First, we pose a Gaussian prior model for the probability distribution of the temperature derivative

$$\begin{aligned} f\sim {\mathcal {N}}(0,\Gamma _{pr}), \end{aligned}$$

(17)

with zero mean and covariance matrix $\Gamma _{pr}$. Here, we define the covariance matrix in terms of the precision matrix $\Gamma _{pr}^{-1}=\gamma ^{-2}L^{T}L$, where $\gamma ^{2}$ is the marginal variance and matrix $L\in {\mathbb {R}}^{m \times m}$ is a model proposed by Bui [29] as follows. We let $f_i=\frac{1}{2}(f_{i+1}+f_{i-1})+\xi _i$, where $\xi _{i }\sim {\mathcal {N}}(0,1)$ for $i=2,\ldots ,m-1$.

For the end points $f_{1}$ and $f_{m}$ we postulate

$$\begin{aligned} f_{1} \sim {\mathcal {N}}\left( 0, \frac{1}{\delta ^{2}}\right) , \quad f_{m} \sim {\mathcal {N}}\left( 0, \frac{1}{\delta ^{2}}\right) , \end{aligned}$$

and set the end points variance $1/\delta ^{2}$ by letting

$$\begin{aligned} \frac{1}{\delta ^{2}}=e_{[m/ 2]}^{T}\left( L_{D}^{T} L_{D}\right) ^{-1} e_{[m/ 2]}, \end{aligned}$$

where $e_{[m/ 2]}$ is the canonical basis vector of index the integer part of $\frac{m}{2}$ and

$$\begin{aligned} L_D = \frac{1}{2} \begin{bmatrix} 2&{}\quad -1\\ -1&{}\quad 2&{}\quad -1\\ &{}&{}\quad \ddots &{}\\ &{}&{}\quad -1&{}\quad 2&{}\quad -1\\ &{}&{}&{}\quad -1&{}\quad 2 \end{bmatrix}\in {\mathbb {R}}^{m \times m }. \end{aligned}$$

Then $\gamma ^{-2}L^{T}L=\Gamma _{pr}^{-1}$ is the precision matrix where

$$\begin{aligned} L = \frac{1}{2} \begin{bmatrix} 2\delta &{}\quad 0\\ -1&{}\quad 2&{}\quad -1\\ &{}&{}\quad \ddots &{}\\ &{}&{}\quad -1&{}\quad 2&{}\quad -1\\ &{}&{}&{}\quad 0&{}\quad 2\delta \end{bmatrix}\in {\mathbb {R}}^{ m \times m }, \end{aligned}$$

The marginal variance $\gamma ^{2}$ is chosen to be a function of the number of degrees of freedom, i.e. $\gamma ^{2}=\gamma _{0} m^{3}$ for some $\gamma _{0} > 0$ and m is the number of degrees of freedom.

Equations (16) and (17), together with Bayes rule (see [30]), define a Gaussian model for the conditional probability of the derivative of the temperature f given a vector of temperature measurements T

$$\begin{aligned} f|T\sim {\mathcal {N}}(f_{post},\Gamma _{post}) \end{aligned}$$

(18)

with explicit expressions for the posterior covariance matrix

$$\begin{aligned} \Gamma _{post} = \left( A^{T}\Gamma _{obs}^{-1}A+\Gamma _{pr}^{-1}\right) ^{-1} = \left( \frac{1}{\gamma _{T}^2}A^{T}A+\frac{1}{\gamma ^2} L^{T}L \right) ^{-1} \end{aligned}$$

(19)

and the posterior mean vector

$$\begin{aligned} f_{post} = \frac{1}{\gamma _{T}^2}\Gamma _{post}A^{T}T. \end{aligned}$$

(20)

The second stage of the inverse problem is carried out through dimension reduction in the number of degrees of freedom.

2.5.2 Dimension reduction

It is known that in the Bayesian approach to inverse problems, the update from prior distribution (17) to posterior distribution (18) occurs along a low-dimensional subspace of the space where the distributed parameter f lies. There are research efforts aimed at understanding, computing, and exploiting those data-informed subspaces in the parameter space, see [9, 31, 32], for both linear and nonlinear inverse problems. Among the data-informed subspace analysis methods, parameter dimension reduction is of paramount importance. Indeed, there is an interplay between smoothness of the forward model (13), the dimension of the parameter space, and the signal to noise ratio that determines the uncertainty in the posterior distribution (18), and this dimension is a feature we can change to reduce the uncertainty in the posterior distribution. In the context of methods for parameter space model reduction, there are approaches based on optimization [10] and approaches based on marginalization [32] among other techniques. It is safe to say that although there are no general parameter dimension reduction methods, most methods aim to enhance the predictive capability of the posterior distribution as a statistical model, e.g., to quantify the uncertainty in the solution of the inverse problem better.

In the present setting, we reduce the dimension of the distributed parameter f, inferred as shown in the Eqs. (18), (20), by computing the pointwise posterior variance and undersampling f at points with smaller variance. To accomplish this task, we use matrix A in Eq. (15) and a linear interpolation $f=Bg$, where $B\in {\mathbb {R}}^{m \times n}$, with $n<m$, is a linear transformation aimed at collocating the degrees of freedom used to represent f. In the present setting, we define B such that Bg it leaves unchanged $r\in {\mathbb {N}}$ degrees of freedom near the endpoints, and undersamples the remainder degrees of freedom every other point.

$$\begin{aligned} B = \begin{bmatrix} I_r &{}\quad {\textbf{0}} &{}\quad {\textbf{0}}\\ {\textbf{0}} &{}\quad R &{}\quad {\textbf{0}} \\ {\textbf{0}} &{}\quad {\textbf{0}} &{}\quad I_r\\ \end{bmatrix}\in {\mathbb {R}}^{ m \times n }, \end{aligned}$$

where $I_r \in {\mathbb {R}}^{r \times r}$ is the identity matrix, ${\textbf{0}}$ are zero matrices and

$$\begin{aligned} R_{} = \begin{bmatrix} 1&{}\quad 0\\ 1/2&{}\quad 1/2&{}\quad 0\\ 0 &{}\quad 1 &{}\quad 0\\ &{}\quad 1/2&{}\quad 1/2&{}\quad 0\\ &{}&{}\quad \ddots &{}\\ \end{bmatrix} \in {\mathbb {R}}^{(m-2r) \times (n-2r)} \end{aligned}$$

is the interpolation matrix, with $n={\left\{ \begin{array}{ll}(m+1)/2 &{} \text {if}\;m\;\text {is odd}\\ m/2 &{} \text {if}\;m\;\text {is even}\end{array}\right. }$.

This collocation strategy reduces both the posterior variance, and the number of degrees of freedom in the distributed parameter g, as we will see in Sect. 3. The forward model (15) is transformed into

$$\begin{aligned} T=ABg+\xi . \end{aligned}$$

Next, we pose a posterior model on g following the derivation of the likelihood (16), as well as the prior model (17) by means of the corresponding marginal variance ${\hat{\gamma }}$ and matrix ${\hat{L}} \in {\mathbb {R}}^{n \times n}$ to define the covariance matrix in order to form the precision matrix ${\hat{\Gamma }}_{pr}^{-1}={\hat{\gamma }}^{-2} {\hat{L}}^{T} {\hat{L}}$. Thus obtaining

$$\begin{aligned} g|T\sim {\mathcal {N}}(g_{post},{\hat{\Gamma }}_{post}) \end{aligned}$$

(21)

where

$$\begin{aligned} {\hat{\Gamma }}_{post} = \left( (AB)^{T}\Gamma _{obs}^{-1}AB+{\hat{\Gamma }}_{pr}^{-1}\right) ^{-1} = \left( \frac{1}{\gamma _{T}^2}B^{T}A^{T}AB+\frac{1}{{\hat{\gamma }}^2} {\hat{L}}^{T} {\hat{L}} \right) ^{-1} \end{aligned}$$

(22)

and

$$\begin{aligned} g_{post} = \frac{1}{\gamma _{T}^2}{\hat{\Gamma }}_{post}B^{T}A^{T}T. \end{aligned}$$

(23)

Table 1 Sobol sensitivity analysis.

3 Results and discussion

3.1 Forward and backward uncertainty analysis

To establish the adequacy of the thermal Li-Ion cell model (1)–(6), we start from synthetic simulated data created with 41,000 time steps. Specifically, we solve the direct problem with the values specified in [5] for an initial temperature of 298 K and a discharge rate of 1C. The time required to reach the cutoff voltage is 4100 s. We have used the forward and backward uncertainty analysis described in Sect. 2.3. First, by carrying out a Sobol sensitivity analysis we examine the contribution of each one of the model parameters $\theta$, defined by equation (7), to the likelihood (8), which is the conditional probability of a set of voltage observations given these parameters. Table 1 offers evidence that all activation energy parameters have a meaningful contribution to the variance of the likelihood. We argue that this is a measure of practical identifiability.

Fig. 1

MCMC convergence. Two lines of evidence of the convergence of the MCMC are, this trace plot of $-\log (\pi _{V|\Theta }(\theta |v)\pi _{\Theta }(\theta ))$ versus the iteration number, and the computed integrated autocorrelation time (IAT) divided by the number of parameters, which in our case is given by $IAT/4=6.8$

Fig. 2

Inference results. Complementary to the Sobol sensitivity analysis shown in Table 1, the posterior distribution is narrower for parameters with larger Sobol sensitivity index.

Fig. 3

Predicted state variables. The predicted temperature and voltage using samples from the posterior distribution obtained through MCMC. Synthetic data was created with 41,000 time steps while samples from the MCMC were created using 4100 points.

Next, we use MCMC to sample iteratively the posterior distribution (11) by means of the t-walk from Christen and Fox [33]. Two standard tests provide numerical evidence of the MCMC convergence, see Roberts and Rosenthal [34]. Namely, the trace plot of $-\log (\pi _{V|\Theta }(\theta |v)\pi _{\Theta }(\theta ))$ versus the iteration number shown in Fig. 1, and the computed integrated autocorrelation time (IAT) divided by the number of parameters, which in our case is given by $IAT/4=13.4$.

Fig. 4

Inference results with a coarse-grained computer model (I). Temperature derivative (a) and temperature (b) inferred with a naive prior model with 4100 uniformly spaced grid points. Parts (c) and (d) shows the corresponding ones with the variance reduction subsampling method described in Sect. 2.5.2

Fig. 5

Inference results with a coarse-grained computer model (II). Reversible heat (a) and voltage (b) inferred with a naive prior model with 4100 uniformly spaced grid points. Parts (c) and (d) shows the corresponding ones with the variance reduction subsampling method described in Sect. 2.5.2

The posterior distribution gives useful information for the identification of model parameters. In particular, by means of the MCMC samples is possible to compute estimators of the posterior distribution (for example, the median $\theta _\textrm{median}$ shown in Fig. 2) with a quantified uncertainty.

Also, this MCMC samples allows us to analyze the relation between forward uncertainty analysis and practical parameter identifiability. Indeed, from Table 1 and Fig. 2 we see that posterior variance is smaller for those parameters with larger sensitivity. This outcome is expected given that carry out a global sensitivity analysis (Sobol) of the likelihood over the whole parameter support. Consequently, a measure of practical identifiability given a data set, is that the Sobol sensitivity index is roughly the same order of magnitude for all parameters. This result should be general given a data set, a likelihood and a parameter support.

Fig. 6

Inference results with a fine-grained computer model (I). Temperature derivative (a) and temperature (b) inferred with a naive prior model with 16400 uniformly spaced grid points. Parts (c) and (d) shows the corresponding ones with the variance reduction subsampling method described in Sect. 2.5.2

Figure 3a and b show, for temperature and voltage respectively, the true value as well as the values predicted by the posterior median and by the 5–95% percentiles of the posterior distribution. We note that predictions are achieved with very low forward uncertainty.

The inference results shown in Figs. 2 and 3 are obtained by simulating the direct problem with 4100 time steps, while synthetic data, as described in Sect. 2.3, was created using 41000 time steps. Indeed, numerical simulations of the direct problem in computer MacBook Pro (15-inch, 2018), 2.6 GHz Intel Core i7 of six cores, with 16 GB 2400 MHz DDR4 take $1.04\;s$ with 4100 points and $5.92\;s$ with 41000 points. Namely, simulating the posterior distribution with the coarse model saves more than 80% computation time. We argue that this computing efficiency is of paramount importance if we are to sample the posterior distribution of the activation energy parameters $\theta$ via MCMC.

3.2 Estimation of the reversible heat

Information about the estimation of the temperature derivative for a coarse-grained computer model (4100 time steps) can be found in Fig. 4a. Figure 4b shows the temperature distribution predicted by multiplying by matrix A, the discrete direct operator defined in Sect. 2.5.1, while Figs. 5a and b show the predicted cell’s reversible heat $q_\textrm{rev}$ and voltage $V_\textrm{cell}$ computed from the temperature. On the other hand, Figs. 4c, d, 5c and d show the corresponding results obtained after computing the pointwise posterior variance and undersample the temperature derivative at the points with smaller variance. For this task, we allocate 10 % of the total initial number of degrees of freedom uniformly placed in a neighborhood of the endpoints, as described in Sect. 2.5.2. Of note, the dimension reduction improves the estimation of the reversible heat, and reduces the posterior variance.

The same analysis is presented in Figs. 6 and 7 for a fine-grained computer model (41000 time steps). This simulation renders roughly the same result as the coarse-grained one. Namely, we obtain roughly the same estimate of the reversible heat and the same uncertainty and predictions of both temperature and voltage. Consequently, it may be preferable to use the coarse-grained model if we have to analyze multiple datasets.

We argue that our inference is robust to the numerical discretization, and subsampling the distributed parameters in the region where the pointwise variance is smaller reduces the variance in the posterior distribution.

Fig. 7

Inference results with a fine-grained computer model (II). Reversible heat (a) and voltage (b) inferred with a naive prior model with 16,400 uniformly spaced grid points. Parts (c) and (d) shows the corresponding ones with the variance reduction subsampling method described in Sect. 2.5.2

4 Conclusions

In this paper, we apply forward and backward uncertainty analysis to assess the adequacy of a thermal single-particle Li-Ion cell model. We have used parameter sensitivity analysis as diagnostics preceding parameter estimation. We offer numerical evidence that forward uncertainty analysis may serve as a practical identifiability test given a set of voltage observations. Afterward, we use error control of the posterior distribution concerning the numerical approximation of the direct problem to reduce the computational burden in approximating such a posterior distribution in order to identify the activation energy parameters via Markov Chain Monte Carlo. In the second part of the manuscript, we infer the reversible heat of a Li-Ion cell given observations of the temperature and an energy balance equation. To accomplish this task, we exploit the linearity of the energy balance equation to construct the solution of the inference problem as a conditional probability given by a Gaussian distribution with explicit expressions for the mean and the covariance, Eqs. (18)–(20). Furthermore, we exploit the fact that the solution grid is different from the data grid to apply a variance reduction method and obtain a posterior distribution with reduced uncertainty, and a smaller number of degrees of freedom, Eqs. (21)–(22), and Algorithm 1.