Skip to main content

Advertisement

SpringerLink
Log in

Uniform interior stabilization for the finite difference fully-discretization of the 1-D wave equation

  • Published:
Afrika Matematika Aims and scope Submit manuscript

Abstract

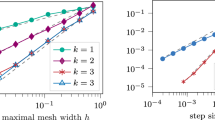
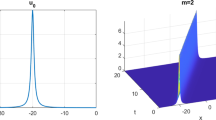
In this paper, we are interested to prove the uniform exponential decay of the energy for the finite difference fully-discretization of 1-D wave equation with an interior damping at \(\xi \). To this end, we decompose the fully discrete system into two subsystems: a conservative system, and a non conservative one. We show under a numerical hypothesis on \(\xi \) that a uniform observability inequality holds for a conservative system, when the mesh size tends to zero using Fourier series technique. Then, we use the observability inequality to prove the uniform exponential decay of the energy for the damped system. Finally, we describe some numerical experiments to illustrate the exponential decay of the energy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Ammari, K., Henrot, A., Tucsnak, M.: Asymptotic behaviour of the solutions and optimal location of the actuator for the pointwise stabilization of a string. Asymptot. Anal. 28, 215–240 (2001)

    MathSciNet  MATH  Google Scholar 

  2. Banks, H.T., Kunisch, K.: The linear regulator problem for parabolic systems. SIAM J. Control Opt. 22, 684–698 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  3. Banks, H.T., Wang, C.: Optimal feedback control of infinite-dimensional parabolic evolution systems: approximation techniques. SIAM J. Control Optim. 27, 1182–1219 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  4. Banks, H.T., Ito, K., Wang, B.: Exponentially stable approximations of weakly damped wave equations. Int. Ser. Numer. Math. 100, 1–33 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bouslous, H., El Boujaoui, H., Maniar, L.: Uniform boundary stabilization for the finite difference semi-discretization of 2-D wave equation. Afr. Mat. 25, 623–643 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  6. Castro, C., Micu, S.: Boundary controllability of a linear semi-discrete 1-D wave equation derived from a mixed finite element method. Numerische Mathematik 102, 413–462 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  7. El Boujaoui, H., Maniar, L., Bouslous, H.: Uniform boundary stabilization for the finite difference discretization of the 1-D wave equation. Afr. Mat. (2016). https://doi.org/10.1007/s13370-016-0406-3

    MathSciNet  MATH  Google Scholar 

  8. Ervedoza, S., Zuazua, E.: Uniformly exponentially stable approximations for a class of damped systems. J. Math. Pures Appl. 91, 20–48 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  9. Glowinski, R., Kinton, W., Wheeler, M.F.: A mixed finite element formulation for the boundary controllability of the wave equation. Int. J. Numer. Methods Eng. 27, 623–635 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  10. Infante, J., Zuazua, E.: Boundary observability for the space semi-discretization of the 1-D wave equation. M2AN 33, 407–438 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  11. Isaacson, E., Keller, H.B.: Analysis of numerical methods. Wiley, New York (1966)

    MATH  Google Scholar 

  12. Leon, L., Zuazua, E.: Boundary controllability of the finite-difference space semi-discretization of the beam equation. ESAIM Control Optim Calc. Var. 8, 827–862 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  13. Loreti, P., Mehrenberger, M.: An Ingham type proof for a two-grid observability theorem. ESAIM Control Optim. Calc. Var. 14, 604–631 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  14. Münch, A., Pazoto, A.F.: Uniform stabilization of a viscous numerical approximation for a locally damped wave equation. ESAIM Control Optim. Calc. Var. 13, 265–293 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  15. Negreanu, M., Zuazua, E.: Uniform boundary controllability of a discrete 1-D wave equation. Syst. Control Lett. 48, 261–280 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  16. Negreanu, M., Zuazua, E.: Convergence of a multigrid method for the controllability of a 1-D wave equation. C. R. Math. Acad. Sci. Paris 338, 413–418 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  17. Nicaise, S., Valein, J.: Stabilization of the wave equation on 1-D networks with a delay term in the nodal feedbacks. Netw. Heterog. Media 2, 425–479 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  18. Nicaise, S., Valein, J.: Quasi exponential decay of a finite difference space discretization of the 1-d wave equation by pointwise interior stabilization. Adv. Comput. Math. 32, 303–334 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  19. Rebarber, R.: Exponential stability of coupled beams with dissipative joints: a frequency domain approach. SIAM J. Control Optim. 33, 1–28 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  20. Tebou, L.T., Zuazua, E.: Uniform exponential long time decay for the space semi-discretization of a locally damped wave equation via an artificial numerical viscosity. Numer. Math. 95, 563–598 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  21. Tebou, L.T., Zuazua, E.: Uniform boundary stabilization of the finite difference space discretization of the 1-d wave equation. Adv. Comput. Math. 26, 337–365 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  22. Zuazua, E.: Boundary observability for the finite difference space semi-discretization of the 2-D wave equation in the square. J. Math. Pures Appl. 78, 523–563 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  23. Zuazua, E.: Controllability of partial differential equations and its semi-discrete approximations. Discrete Contin. Dyn. Syst. 8, 469–513 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  24. Zuazua, E.: Propagation, observation, control and numerical approximation of waves. SIAM Rev. 47, 197–243 (2005)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. National School of Applied Sciences, Ibn Zohr University, B.P. 1136, Agadir, Morocco

    H. El Boujaoui

Authors
  1. H. El Boujaoui
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to H. El Boujaoui.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

El Boujaoui, H. Uniform interior stabilization for the finite difference fully-discretization of the 1-D wave equation. Afr. Mat. 29, 557–574 (2018). https://doi.org/10.1007/s13370-018-0559-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13370-018-0559-3

Keywords

Mathematics Subject Classification

Search

Navigation