Skip to main content
SpringerLink
Log in

An Improved Creep Model for Granite Based on the Deviatoric Stress-to-Peak Strength Ratio

  • Research Article-Civil Engineering
  • Published:
Arabian Journal for Science and Engineering Aims and scope Submit manuscript

Abstract

Time-dependent behaviors of rocks can be attributed to long-term applied stress, which occurs in most underground engineering projects. The creep behavior of granite from the Shuangjiangkou underground powerhouse in western Sichuan Province, China, was investigated via creep tests. It is shown that granite has an obvious creep behavior under different confining pressures and deviatoric stresses. The new dimensionless parameter DPR, which is defined as the ratio of the deviatoric stress to the peak strength, is proposed for experimental analysis. The relationships between the instantaneous strain and final visco-elastic creep strain of granite with DPR are established under different confining pressures. It is shown that when DPR is equal to 0.63, the final visco-elastic creep strain of rocks will reach a minimum value. Based on DPR and the secondary creep strain rate, a unified method for defining the long-term strength of rocks is proposed, and the granite will enter in secondary creep with a nonzero strain rate when DPR > 0.9501. The Nishihara model is improved, and the relationships between the parameters of the improved model with confining pressures and DPR are obtained. The improved creep model can satisfactorily represent the primary creep strain of granite and secondary creep strain of granite with time under a given confining pressure and deviatoric stress.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

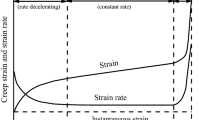
adapted from Goodman [13])

Fig. 2
Fig. 3
Fig. 4
Fig. 5

(adapted from Zhao et al. [15])

Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Code availability

Not applicable.

References

  1. Brantut, N.; Heap, M.J.; Meredith, P.G.; Baud, P.: Time-dependent cracking and brittle creep in crustal rocks: a review. J. Struct. Geol. 52(5), 17–43 (2013)

    Article  Google Scholar 

  2. Sun J.: Rock rheological mechanics and its advance in engineering applications. Chinese Journal of Rock Mechanics and Engineering. 26(6), 1081–1106 (2007) (in Chinese)

  3. Bourgeois, F.; Shao, J.F.; Ozanam, O.: An elastoplastic model for unsaturated rocks and concrete. Mech. Res. Commun. 29(5), 383–390 (2002)

    Article  Google Scholar 

  4. Zhang, Y.; Xu, W.Y.; Shao, J.F.; Zhao, H.B.; Wang, W.: Experimental investigation of creep behavior of clastic rock in Xiangjiaba Hydropower Project. Water Science and Engineering. 8(1), 55–62 (2015)

    Article  Google Scholar 

  5. Bayraktar, A.; Kartal, M.E.; Basaga, H.B.: Reservoir water effects on earthquake performance evaluation of Torul concrete-faced rockfill dam. Water Science and Engineering. 2(1), 43–57 (2009). https://doi.org/10.3882/j.issn.1674-2370.2009.01.005

    Article  Google Scholar 

  6. Yang, W.; Zhang, Q.; Li, S.; Wang, S.: Time-dependent behavior of diabase and a nonlinear creep model. Rock Mech. Rock Eng. 47(4), 1211–1224 (2014)

    Article  Google Scholar 

  7. Boukharov, G.N.; Chanda, M.W.: The three processes of brittle crystalline rock creep. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 32(4), 325–335 (1995)

    Article  Google Scholar 

  8. Dusseault M.B., Fordham C.J.: Time dependent behaviour of rocks. In: Comprehensive Rock Engineering: Principles, Practice and Projects. Pergamon Press, Oxford, UK, 119–149 (1993)

  9. Wang R., Li L., Simon R.: A model for describing and predicting the creep strain of rocks from the primary to the tertiary stage. International Journal of Rock Mechanics and Mining Sciences. 123, 104087 (2019)

  10. Cristescu N.D., Hunsche U.: Time Effects in Rock Mechanics. Wiley, New York, NY, USA, 53 (1998)

  11. Malan, K.; Vogler, U.W.; Drescher, K.: Time-dependent behaviour of hard rock in deep level gold mines. Journal South African Institute of Mining & Metallurgy. 97(3), 135–147 (1997)

    Google Scholar 

  12. Malan, D.F.: Time-dependent behaviour of deep level tabular excavations in hard rock. Rock Mech. Rock Eng. 32(2), 123–155 (1999)

    Article  Google Scholar 

  13. Goodman R.: Introduction to rock mechanics. Wiley, New York, NY, USA, 129–149 (1989)

  14. Amitrano, D.; Helmstetter, A.: Brittle creep, damage, and time to failure in rock. J. Geophys. Res. 111(B11201), 1–17 (2006)

    Google Scholar 

  15. Zhao, Y.; Wang, Y.; Wang, W.; Wan, W.; Tang, J.: Modeling of non-linear rheological behavior of hard rock using triaxial rheological experiment. Int. J. Rock Mech. Min. Sci. 93, 66–75 (2017)

    Article  Google Scholar 

  16. Zhang, H.; Wang, Z.; Zheng, Y.; Duan, P.; Ding, S.: Study on tri-axial creep experiment and constitutive relation of different rock salt. Saf. Sci. 50(4), 801–805 (2012)

    Article  Google Scholar 

  17. Ngwenya, B.T.; Main, I.G.; Elphick, S.C.; Crawford, B.; Smart, B.G.D.: A constitutive law for low-temperature creep of water-saturated sandstones. Journal of Geophysical Research Solid Earth. 106, 21811–21826 (2001)

    Article  Google Scholar 

  18. Campanella, R.G.; Vaid, Y.P.: Triaxial and plane strain creep rupture of an undisturbed clay. Can. Geotech. J. 11(1), 1–10 (1974)

    Article  Google Scholar 

  19. Lajtai, E.Z.; Schmidtke, R.H.: Delayed failure in rock loaded in uniaxial compression. Rock Mech. Rock Eng. 19(1), 11–25 (1986)

    Article  Google Scholar 

  20. Yu, M.; Mao, X.; Hu, X.: Shear creep characteristics and constitutive model of limestone. International Journal of Mining Science and Technology. 26, 423–428 (2016)

    Article  Google Scholar 

  21. Wang R., Li L.: A non-stationary power law model to predict the secondary creep rate of rocks. Proceedings of 8th International Conference on Case Histories in Geotechnical Engineering. (2019)

  22. Bazant, Z.P.; Xi, Y.: Drying creep of concrete: constitutive model and new experiments separating its mechanism. Mater. Struct. 27(1), 3–14 (2019)

    Article  Google Scholar 

  23. Tang, S.; Green, M.S.; Liu, W.K.: Two-scale mechanism-based theory of non-linear viscoelasticity. J. Mech. Phys. Solids 60(2), 199–226 (2012)

    Article  MathSciNet  Google Scholar 

  24. Shao, J.F.; Zhu, Q.Z.; Su, K.: Modeling of creep in rock materials in terms of material degradation. Comput Geotech. 30, 549–555 (2003)

    Article  Google Scholar 

  25. Chen, L.; Wang, C.P.; Liu, J.F.; Liu, Y.M.; Liu, J.; Su, R.; Wang, J.: A damage-mechanism-based creep model considering temperature effect in granite. Mech. Res. Commun. 56, 76–82 (2014)

    Article  Google Scholar 

  26. Zhang S., Liu W., Zhang Y., Lin X.: Creep damage analysis of granite based on the principle of minimum energy consumption. Journal of basic science and engineering. 27(1), 210–220 (2019) (in Chinese)

  27. Hu, K.; Feng, Q.; Li, H.; Hu, Q.: Study on creep characteristics and constitutive model for thalam rock mass with fracture in tunnel. Geotech. Geol. Eng. 36, 827–834 (2018)

    Article  Google Scholar 

  28. Maranini, E.; Yamaguchi, T.: A non-associated viscoplastic model for the behavior of granite in triaxial compression. Mech. Mater. 33(5), 283–293 (2001)

    Article  Google Scholar 

  29. Mansouri, H.; Ajallocian, R.: Mechanical behavior of salt rock under uniaxial compression and creep tests. Int. J. Rock Mech. Min. Sci. 110, 19–27 (2018)

    Article  Google Scholar 

  30. Wang, R.; Zhuo, Z.; Zhou, H.W.; Liu, J.F.: A fractal derivative constitutive model for three stages in granite creep. Results in Physics. 7, 2632–2638 (2017)

    Article  Google Scholar 

  31. Singh, A.; Kumar, C.; Kannan, G.; Rao, K.S.; Ayothiraman, R.: Estimation of creep parameters of rock salt from uniaxial compression tests. Int. J. Rock Mech. Min. Sci. 107, 243–248 (2018)

    Article  Google Scholar 

  32. Liu, X.: Introduction to rock rheology. Geological Publishing House. Beijing, China (1994)

    Google Scholar 

  33. Nielsen, L.E.; Landel, R.F.: Mechanical Properties of Polymers and Composites. New York. New York, USA, M Dekker (1993)

    Google Scholar 

  34. Xia, C.C.; Zhong, S.Y.: Experimental data processing method in consideration of influence of loading history on rock specimen deformation. Journal of Central-South Institute of Mining and Metallurgy. 20, 18–24 (1989)

    Google Scholar 

  35. Fahimifar, A.; Karamia, M.; Fahimifar, A.: Modifications to an elasto-visco-plastic constitutive model for prediction of creep deformation of rock samples. Soils Found. 55(6), 1364–1371 (2015)

    Article  Google Scholar 

  36. Sterpi, D.; Gioda, G.: Visco-Plastic Behaviour around dvancing Tunnels in Squeezing Rock. Rock Mech. Rock Eng. 42, 319–339 (2009)

    Article  Google Scholar 

  37. Liu W., Zhang S., Li R.: Accelerated creep model of rock based on energy dissipation theory. Journal of China Coal Society. 44(9). 2741–2750 (2019) (in Chinese)

  38. Zhang, S.; Liu, W.; Lv, H.: Creep energy damage model of rock graded loading. Results in Physics 12, 1119–1125 (2019)

    Article  Google Scholar 

  39. Cong, L.; Hu, X.: Triaxial rheological property of sandstone under low confining pressure. Eng. Geol. 231, 45–55 (2017)

    Article  Google Scholar 

  40. Liu, H.Z.; Xie, H.Q.; He, J.D.; Xiao, M.L.: Nonlinear creep damage constitutive model for soft rocks. Mech Time-Depend Mater. 21, 73–96 (2017)

    Article  Google Scholar 

  41. R.B. Hou, Kai Zhang, J. Tao, X.R. Xue, Y.L. Chen: A nonlinear creep damage coupled model for rock considering the effect of initial damge. Rock Mechanics and Rock Engineering. 52: 1275–1285 (2019)

  42. Lyu H.M., LIU W.B.: Study on creep damage model of granite in Gaode Coal Mine. Coal Science and Technology. 47(3): 125–130 (2019) (in Chinese)

  43. S.J, Niu, W.L. Feng, Jin Yu, C.S. Qiao, S.X. Liu, Y.B. Sun: Experimental study on the mechanical properties of short-term creep in post-peak rupture damaged sanstone. Mech Time-Depend Mater (2019) https://doi.org/https://doi.org/10.1007/s11043-019-09431-2

  44. Xiao F.K., Li R.H., Li L.C., Hou Z.Y.: Deformation and internal damage properties of coal under hierarchical constant load. Journal of Heilongjiang University of Science & Technology. 30(1): 1–7 (2020) (in Chinese)

  45. Wang L., GUO C.B., GUO P.Y., JI F.: Creep character and constitutive model of gneiss in Zilashan area of Sichuan-Tibet railway line. Ceoscience (2020) https://doi.org/https://doi.org/10.19657/j.geoscience.1000-8527.2021.008 (in Chinese)

  46. Li Y.L., Yu H.C., Liu H.D.: Study of creep constitutive model of silty mudstone under triaxial compression. Rock and Soil Mechanics. 33(7): 2035–2040, 2047 (2012) (in Chinese)

  47. Zhang Q., Shen M, Ding W.: Study of mechanical properties and long-term strength of Jinping green schist. Chinese Journal of Rock Mechanics and Engineering. 31(8), 1642–1649 (2012) (in Chinese)

  48. Wu D-S, Meng L-B, Li T-B, Lai L.: Study of triaxial rheological property and long−term strength of limestone after high temperature. Rock and Soil Mechanics. 37(s1), 183–191 (2016) (in Chinese)

  49. Cui X., Fu Z.: Experiment study on rheology properties and long-term strength of rocks. Chinese Journal of Rock Mechanics and Engineering. 25(5), 1021–1024 (2006) (in Chinese)

  50. Li L-Q, Xu W-Y, Wang W., Guo Y-Q: Estimation of long-term strength for Xiangjiaba sandstone based on creep tests. Engineering Mechanics. 27(11), 127–143 (2010) (in Chinese)

  51. Liu, J.; Wang, S.; Yang, H.: Method to determination the rheological test long-term strength for soft intercalations. Site Investigation Science and Technology 5, 3–7 (1996)

    Google Scholar 

Download references

Acknowledgments

The authors acknowledge the financial support from the National Natural Science Foundation of China (grant number U1965203) and ‘The research on support time and deformation warning of surrounding rock of large underground cavern group under extremely high stress condition of Shuangjiangkou Hydropower’ (grant number A147 SG). The authors thank Professor Jianfeng Liu for his guidance with the tests.

Funding

The National Natural Science Foundation of China (grant number U1965203) and the research on support time and deformation warning of surrounding rock of large underground cavern group under extremely high stress condition of Shuangjiangkou Hydropower (grant number A147 SG).

Author information

Authors and Affiliations

  1. State Key Laboratory of Hydraulics and Mountain River Engineering, College of Water Resources and Hydropower, Sichuan University, Chengdu, 610065, China

    Li Qian, Jianhai Zhang, Xianliang Wang, Ru Zhang & Nuwen Xu

  2. Power China Chengdu Engineering Corporation Limited, Chengdu, 610072, China

    Yonghong Li & Zhiguo Li

Authors
  1. Li Qian
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jianhai Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xianliang Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yonghong Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Ru Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Nuwen Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Zhiguo Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Li Qian performed the experiment and the data analyses, and wrote the manuscript. Jianhai Zhang and Xianliang Wang participated in part of the experiment and helped perform the analysis with constructive discussions. Yonghong Li and Zhiguo Li prepared for samples of the experiment and checked the results of the test. Ru Zhang and Nuwen Xu conceived and designed the analysis.

Corresponding author

Correspondence to Li Qian.

Ethics declarations

Conflict of interest

The authors declare there is no conflicts of interest regarding the publication of this paper.

Availability of data and material

All data generated or analyzed during this study are included in this published article.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Qian, L., Zhang, J., Wang, X. et al. An Improved Creep Model for Granite Based on the Deviatoric Stress-to-Peak Strength Ratio. Arab J Sci Eng 46, 5157–5170 (2021). https://doi.org/10.1007/s13369-021-05441-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13369-021-05441-w

Keywords

Search

Navigation