Skip to main content

Advertisement

SpringerLink
Log in

Analytical Modeling and Vibration Analysis of the Last-Stage LP Steam Turbine Blade Made of Functionally Graded Material

  • Research Article-Mechanical Engineering
  • Published:
Arabian Journal for Science and Engineering Aims and scope Submit manuscript

Abstract

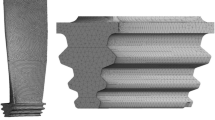
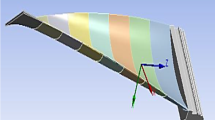
The conventional materials used in steam turbine blades undergo severe environmental loading conditions resulting in  corrosion, fatigue failures, and several kinds of defects. Especially for the last-stage steam turbine blade, there is a need to employ hybrid materials such as functionally graded (FG) materials or other composites that combine the properties of two or more desired materials to withstand extreme conditions without much loss of blade output. The present paper includes the theoretical investigation of free vibration study of the regular last-stage low-pressure steam turbine blade using the Finite element method via the in-house codes. Further, the structural modeling of the functionally graded blade and its free vibration characteristics are evaluated. The dynamic equations of motion of the functionally graded blade are derived by considering geometric taper. The impact of several factors, such as the volume fraction index, rotational speed, and twist angle on the natural frequencies of the FG rotating blade, is reported at different speeds of operation. It is observed that with an increase in volume fraction index, both chordwise and flapwise bending frequencies decrease; however, the rate of decrease is higher in higher modes. The opposite trend is observed in the FG blade’s vibratory characteristics with respect to the rotational speed and twist angle.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Krylov, N.A.; Skotnikova, M.A.; Tsvetkova, G.V.; Ivanova, G.V.: Resistance to erosive destruction of steam turbine blades from titanium alloys, their structure, and phase composition. Mater. Phys. Mech. 39, 128–134 (2017)

    Google Scholar 

  2. Carnegie, W.: Vibration of pre-twisted cantilever blading. Proc. Int. Mech. Eng. 173, 343–374 (1959)

    Article  Google Scholar 

  3. Houbolt, J.C., Brooks G.W.: Differential equations of motion for combined flapwise bending chordwise bending and torsion of twisted non-uniform rotor blades. NACA Report 1346 (1958)

  4. Dawson, B.; Ghosh, N.G.; Carnegie, W.: Effect of slenderness ratio on the natural frequencies of pre-twisted cantilever beams of uniform rectangular cross-section. J. Mech. Eng. Sci. 13, 51–59 (1971)

    Article  Google Scholar 

  5. Carnegie, W.: The application of the variational method to derive the equation of motion of vibrating cantilever blading under rotation. Bull. Mech. Eng. Educ. 6, 29–38 (1967)

    Google Scholar 

  6. Thomas, J.; Abbas, B.: Finite element model for dynamic analysis of Timoshenko beams. ASME J. Sound Vib. 41, 291–299 (1976)

    Article  Google Scholar 

  7. Rosard, D.; Lester, P.: Natural frequency of twisted cantilever beam. ASME J. Appl. Mech. 17, 241–244 (1999)

    Google Scholar 

  8. Hoa, S.V.: Vibration of a rotating beam with tip mass. J. Sound Vib. 67(3), 369–381 (1979)

    Article  MATH  Google Scholar 

  9. Chen, Y.; Zhang, J.; Zhang, H.: Free vibration analysis of rotating tapered Timoshenko beams via the variational iteration method. J. Vib. Control 23, 1–15 (2015)

    MathSciNet  Google Scholar 

  10. Karadag, V.: Dynamic analysis of practical blades with shear center effect. J. Sound Vib. 92, 471–490 (1984)

    Article  Google Scholar 

  11. Lee, S.Y.; Kuo, Y.H.: Elastic stability of non-uniform columns. J. Sound Vib. 148(1), 11–24 (1991)

    Article  Google Scholar 

  12. Sarkar, K.; Ganguli, R.: Modal tailoring and closed-form solutions for rotating non-uniform Euler-Bernoulli beams. Int. J. Mech. Sci. 88, 208–212 (2014)

    Article  Google Scholar 

  13. Sina, S.; Haddadpour, H.: Axial-torsional vibrations of rotating pre-twisted thin-walled composites beams. Int. J. Mech. Sci. 80, 93–101 (2014)

    Article  Google Scholar 

  14. Chandiramani, N.; Shete, C.; Librescu, L.: Vibration of higher-order-shearable pre-twisted rotating composite blades. Int. J. Mech. Sci. 45, 2017–2041 (2003)

    Article  MATH  Google Scholar 

  15. Yoo, H.H.; Kwak, J.Y.; Chung, J.: Vibration analysis of rotating pre-twisted blades with a concentrated mass. J. Sound Vib. 240(5), 891–908 (2001)

    Article  Google Scholar 

  16. Na, S.; Librescu, L.; Shim, K.: Modeling and bending vibration control of non-uniform thin-walled rotating beams incorporating adaptive capabilities. Int. J. Mech. Sci. 45, 1347–1367 (2003)

    Article  MATH  Google Scholar 

  17. Subrahmanyam, K.B.: Coupled bending-bending vibrations of pre-twisted tapered cantilever beams treated by the Reissner method. J. Sound Vib. 82(4), 577–592 (1982)

    Article  Google Scholar 

  18. Chen, C.K.; Ho, S.H.: Transverse vibration of a rotating twisted Timoshenko beam under axial loading using differential transform. Int. J. Mech. Sci. 41, 1339–1356 (1999)

    Article  MATH  Google Scholar 

  19. Oh, Y.; Yoo, H.H.: Vibration analysis of a rotating pre-twisted blade considering the coupling effects of stretching, bending, and torsion. J. Sound Vib. 431, 20–39 (2018)

    Article  Google Scholar 

  20. Oh, Y.; Yoo, H.H.: Vibration analysis of rotating pre-twisted tapered blades made of functionally graded materials. Int. J. Mech. Sci. 119, 68–79 (2016)

    Article  Google Scholar 

  21. Qian, X.; Dutta, D.: Design of heterogeneous turbine blade. Computer Aided Des. 35, 319–329 (2003)

    Article  Google Scholar 

  22. Fang, J.; Zhou, D.; Dong, Y.: Three-dimensional vibration of rotating functionally graded beams. J. Vib. Control. 12, 1–15 (2017)

    Google Scholar 

  23. Silambarasan, M.; Arivazhagan, K.: Developing the steam turbine blades by using various materials instead of existing one and conducting the stress analysis. Int. J. Latest Trends Eng. Technol. 8(2), 358–366 (2018)

    Google Scholar 

  24. Dong, S.; Li, L.; Zhang, D.: Vibration analysis of rotating functionally graded tapered beams with hollow circular cross-section. Aerosp. Sci. Technol. 95, 105476 (2019)

    Article  Google Scholar 

  25. Rafieea, M.; Nitzscheb, F.; Labrossea, M.: Dynamics, vibration and control of rotating composite beams and blades. Thin-Walled Struct. 119, 795–819 (2017)

    Article  Google Scholar 

  26. Cao, D.X.; Liu, B.Y.; Yao, M.H.; Zhang, W.: Free vibration analysis of a pre-twisted sandwich blade with thermal barrier coatings layers. Sci. China Technol. Sci. 60(11), 1747–1761 (2017)

    Article  Google Scholar 

  27. Şimşek, M.: Static analysis of a functionally graded beam under a uniformly distributed load by Ritz method. Int. J. Eng. Appl. Sci. 1, 1–11 (2009)

    Google Scholar 

  28. Cheng, J.; Xu, H.; Yan, A.: Frequency analysis of a rotating cantilever beam using assumed mode method with coupling effect. Mech. Based Des. Struct. Mach. 34, 25–47 (2006)

    Article  Google Scholar 

  29. Kumar, P.R.; Rao, K.M.; Rao, N.M.: Free vibration analysis of functionally graded rotating beam by differential transform method. Indian J. Eng. Mate Sci. 24, 107–114 (2017)

    Google Scholar 

  30. Piovan, M.T.; Sampaio, R.: A study on the dynamics of rotating beams with functionally graded properties. J. Sound Vib. 327, 134–143 (2009)

    Article  Google Scholar 

  31. Ramesh, M.N.V.; Mohan-Rao, N.: Flapwise bending vibration analysis of functionally graded rotating double-tapered beams. Int. J. Mech. Mate. Eng. 16, 1 (2015)

    Google Scholar 

  32. Sina, S.A.; Haddadpour, H.: Axial torsional vibrations of rotating pretwisted thin walled composite beams. Int. J. Mech. Sci. 80, 93–101 (2014)

    Article  Google Scholar 

  33. Ramesh, M.N.V.; Rao, N.M.: Free Vibration Analysis of Rotating Functionally-Graded Cantilever Beams. Int. J. Acoust. Vib. 19(1), 31–41 (2014)

    Google Scholar 

  34. Yoo, H.H.; Ryan, R.R.; Scott, R.A.: Dynamics of flexible beams undergoing overall motion. J. Sound. Vib. 181(2), 261–278 (1995)

    Article  MATH  Google Scholar 

  35. Ebrahimi, F.; Mokhtari, M.: Free vibration analysis of a rotating Mori–Tanaka-based functionally graded beam via differential transformation method. Arab J Sci Eng. 41, 577–590 (2016)

    Article  Google Scholar 

  36. Sina, S.A.; Navazi, H.M.; Haddadpour, H.: An analytical method for free vibration analysis of functionally graded beams. Mater. Des. 30, 741–747 (2009)

    Article  Google Scholar 

  37. Liang, X.; Hu, S.; Shen, S.: A new Bernoulli–Euler beam model based on a simplified strain gradient elasticity theory and its applications. Compos. Struct. 111, 317–323 (2014)

    Article  Google Scholar 

  38. Kane, T.R.; Levinson, D.A.: Dynamics: theory and applications. McGraw-HillBook Co, New York (1985)

    Google Scholar 

  39. Yoo, H.H.; Shin, S.: Vibration analysis of rotating cantilever beams. J. Sound. Vib. 212, 807–828 (1998)

    Article  Google Scholar 

  40. Ni, Z.H.H.: Vibration Mechanics. Xi’an Jiaotong University Press, Xi’an (1990)

    Google Scholar 

  41. Zienkiewic, O.C.: The Finite Element Method, 3rd edn. McGraw-Hill, London (1977)

    Google Scholar 

  42. Rao, S.S.; Gupta, R.S.: Finite element vibration analysis of rotating Timoshenko beams. J. Sound Vib. 242(1), 103–124 (2001)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, National Institute of Technology, Rourkela, Odisha, India

    Keshav Alias Deepesh Ramesh Shetkar & J. Srinivas

Authors
  1. Keshav Alias Deepesh Ramesh Shetkar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. Srinivas
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Keshav Alias Deepesh Ramesh Shetkar.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shetkar, K.A.D.R., Srinivas, J. Analytical Modeling and Vibration Analysis of the Last-Stage LP Steam Turbine Blade Made of Functionally Graded Material. Arab J Sci Eng 46, 7363–7377 (2021). https://doi.org/10.1007/s13369-020-05203-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13369-020-05203-0

Keywords

Search

Navigation