Skip to main content
SpringerLink
Log in

Stimulated Reservoir Volume Estimation and Analysis of Hydraulic Fracturing in Shale Gas Reservoir

  • Research Article - Petroleum Engineering
  • Published:
Arabian Journal for Science and Engineering Aims and scope Submit manuscript

Abstract

Hydraulic fracturing in horizontal well is the key technology for the commercial exploitation of shale gas reservoir. Stimulated reservoir volume (SRV) is an important indicator to evaluate the fracturing performance. However, estimating the SRV has been a long-standing challenge due to its complex forming mechanism. Most current SRV estimation methods are either expensive or time-consuming. This paper developed a 3D mathematical model to estimate the SRV by simulating the four main processes during shale fracturing—multiple hydraulic fractures propagation, formation stress variation, reservoir pressure lifting and natural fractures failure. In this model, hydraulic fractures propagation is calculated by pseudo-three-dimensional model, coupling with formation stress model; formation stress and reservoir pressure are obtained by displacement discontinuity method and Green’s function approach, respectively; natural fracture failure criterion is derived from Warpinski’s theory. This model not only considers the stress interference effect of multiple fractures, but also subdivides the SRV into shear-SRV and tensile-SRV according to the failure type of natural fractures network. This model was first implemented to a pilot well in the FL gas field in southwest China to estimate a SRV that matches well with the on-site monitoring microseismic signals. Then, this model was applied to FL gas field on a large scale to evaluate the overall fracturing effects. Finally, a sensitivity study was conducted to analyze the impact of engineering parameters on the SRV. This research explores an efficient method to estimate the SRV without high cost or complicated process and provides the theoretical basis and guidelines for pre-fracturing design and post-fracturing evaluation in shale gas reservoir.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

\((A_\mathrm{nn})_{ij}\) :

Plane-strain, elastic-influence coefficient matrix representing the normal stress at element i induced by normal-displacement discontinuity at element \(j; i, j \in \{1, 2, {\ldots }, N\}\)

\((A_\mathrm{nt})_{ij}\) :

Plane-strain, elastic-influence coefficient matrix representing the normal stress at element i induced by shear-displacement discontinuity at element \(j; i, j \in \{1, 2, {\ldots }, N\}\)

\((A_\mathrm{tn})_{ij}\) :

Plane-strain, elastic-influence coefficient matrix representing the shear stress at element i induced by normal-displacement discontinuity at element \(j; i, j \in \{1, 2, {\ldots }, N\}\)

\((A_\mathrm{tt})_{ij}\) :

Plane-strain, elastic-influence coefficient matrix representing the shear stress at element i induced by shear-displacement discontinuity at element \(j; i, j \in \{1, 2, {\ldots }, N\}\)

\(c_\mathrm{L}\) :

Filtration coefficient (\(\hbox {m/s}^{0.5}\))

E :

Young’s modulus of formation rock (\(\hbox {Pa}^{-1}\))

:

Force vector imposed on the unit area of fracture surface (Pa)

\(F_{i}\) :

Derivatives functions, \(i \in \{3, 4, 5, 6\}\),

G :

Formation shear modulus (\(\hbox {Pa}^{-1}\))

\(h_\mathrm{f}\) :

Fracture height (m)

\(h_\mathrm{r}\) :

Thickness of reservoir (m);

\(h_\mathrm{rD}\) :

Dimensionless thickness of reservoir

\(K_{0}\) :

Zeroth-order Bessel function

\(K_\mathrm{f}\) :

Friction coefficient of natural fracture

\(K_\mathrm{IC}\) :

Fracture toughness (\(\hbox {Pa}\,\hbox {m}^{0.5}\))

\(k_\mathrm{m}\) :

Average permeability of matrix system (D)

\(k_\mathrm{mx}\) :

x-Directional permeability of matrix system (D)

L :

Arbitrary reference length (m)

\(L_\mathrm{f}\) :

Fracture half-length (m)

M :

Number of hydraulic fractures

N :

Number of discontinuous fracture elements

\(n_{i}\) :

Component of

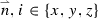
\(N_\mathrm{IL}\) :

An even number between 6 and 18

p :

Current reservoir pressure (Pa)

\(p_{0}\) :

Initial reservoir pressure (Pa)

\(p_\mathrm{f}\) :

Fluid pressure in fracture (Pa)

\(p_{{\mathrm{f}, i}}\) :

Fluid pressure in fracture, \(i \in \{1, 2,\ldots {M}\}\,(\hbox {m}^{3}/\hbox {s}\))

\(p_\mathrm{fnet}\) :

Net pressure in fracture (Pa)

\(p_\mathrm{nf}\) :

Fluid pressure in natural fracture (reservoir pressure) (Pa)

\({\tilde{q}}\) :

Filtration rate per unit area (m/s)

q :

Flow rate in fracture (\(\hbox {m}^{3}/\hbox {s}\))

\(Q_{i}\) :

Inlet flow rate of each fracture \(i \in \{1, 2,\ldots {M}\}(\hbox {m}^{3}/\hbox {s}\))

\(Q_\mathrm{pump}\) :

Pump rate (\(\hbox {m}^{3}/\hbox {s}\))

s :

Laplace transform variable

\(S_\mathrm{t}\) :

Tensile strength of natural fracture (Pa)

t :

Time (s)

u :

Defined function

\(\left( {\hat{{u}}_{\mathrm{n}} }\right) _i\) :

Normal strain of element i in local coordinate, \(i \in \{1, 2,\ldots {N}\}\,(\hbox {m})\)

\(\left( {\hat{{u}}_{\mathrm{t}} }\right) _i\) :

Shear strain of element i in local coordinate, \(i \in \{1, 2,\ldots {N}\}\,(\hbox {m})\)

\(W_\mathrm{f}\) :

Fracture width (m)

\(x_\mathrm{D}\) :

Dimensionless x value

\(x_\mathrm{wD}\) :

Dimensionless x value at perforation point

\(y_\mathrm{D}\) :

Dimensionless y value

\(y_\mathrm{wD}\) :

Dimensionless y value at perforation point

\(z_\mathrm{w}\) :

z value at cluster point (m)

\(\alpha \) :

Integration variable

\(\delta \) :

Kronecker delta

\(\Delta p\) :

Pressure increment field in the real domain (Pa)

\({\Delta }\bar{{p}}\) :

Reservoir pressure increment in Laplace domain (Pa)

\(\Delta p_{i}\) :

Pressure increment, induced by fluid leak-off from fracture \(i, i \in \{1, 2,\ldots {M}\}\,(\hbox {Pa})\)

\(\Delta \sigma _{ij}\) :

Components of induced stress tensor, \(i, j \in \{x, y, z\}\,(\hbox {Pa})\);

\(\theta \) :

Approaching angle of natural fracture (\({}^{\circ }\))

\(\varphi \) :

Dip angle of natural fracture (\({}^{\circ }\))

\(\mu \) :

Viscosity of fracturing fluid (\(\hbox {Pa}\,\hbox {s}\))

\(\nu \) :

Poisson ratio

\(\sigma _{ij}\) :

Components of current formation stress tensor, \(i, j \in \{x, y, z\}\) (Pa)

\(\sigma _{ij}^{\left( 0\right) }\) :

Components of original formation stress tensor, \(i, j \in \{x, y, z\}\) (Pa)

:

Formation stress tensor (Pa)

\(({\sigma }_\mathrm{n})_{i}\) :

Normal stress on element i in local coordinate, \(i \in \{1, 2,\ldots N\}\) (Pa)

\(({\sigma }_\mathrm{t})_{i}\) :

Shear stress on element i in local coordinate, \(i \in \{1, 2,\ldots N\}\) (Pa)

\({\sigma }_\mathrm{n}\) :

Normal stress imposed on fracture surface (Pa)

\({\sigma }_{\tau }\) :

Shear stress imposed on natural fracture (Pa)

\({\tau }\) :

Start time of filtration in fracture (s)

\({\tau }_\mathrm{o}\) :

Cohesive strength of natural fracture (Pa)

References

  1. Luffel, D.L.; Hopkins, C.W.; Schettler, P.D., Jr.: Matrix permeability measurement of gas productive shales. In: Paper SPE 26633 Presented at the SPE Annual Technical Conference and Exhibition, Houston, Texas (1993). https://doi.org/10.2118/26633-MS

  2. Sakhaee-Pour, A.; Bryant, S.: Gas permeability of shale. SPE Reserv. Eval. Eng. 15(04), 401–409 (2012). https://doi.org/10.2118/146944-pa

    Article  Google Scholar 

  3. Ben, Y.; Miao, Q.; Wang, Y.; Shi, G.-h.: Effect of Natural Fractures on Hydraulic Fracturing. In: Paper ISRM-ARMS7-2012-087 Presented at the ISRM Regional Symposium—7th Asian Rock Mechanics Symposium, Seoul, Korea (2012)

  4. Cho, Y.; Ozkan, E.; Apaydin, O.G.: Pressure-dependent natural-fracture permeability in shale and its effect on shale-gas well production. SPE Reserv. Eval. Eng. 16(02), 216–228 (2013). https://doi.org/10.2118/159801-PA

    Article  Google Scholar 

  5. Hu, D.; Matzar, L.; Martysevich, V.N.: Effect of natural fractures on eagle ford shale mechanical properties. In: Paper SPE 170651 Presented at the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands (2014). https://doi.org/10.2118/170651-MS

  6. King, G.E.: Thirty years of gas shale fracturing: what have we learned? In: Paper SPE 133456 Presented at the SPE Annual Technical Conference and Exhibition, Florence, Italy (2010). https://doi.org/10.2118/133456-MS

  7. Wu, Q.; Xu, Y.; Wang, X.; Wang, T.; Zhang, S.: Volume fracturing technology of unconventional reservoirs: connotation, design optimization and implementation. Pet. Explor. Dev. 39(3), 377–384 (2012). https://doi.org/10.1016/S1876-3804(12)60054-8

    Article  Google Scholar 

  8. Zhao, Y.L.; Zhang, L.H.; Luo, J.X.; Zhang, B.N.: Performance of fractured horizontal well with stimulated reservoir volume in unconventional gas reservoir. J. Hydrol. 512, 447–456 (2014). https://doi.org/10.1016/j.jhydrol.2014.03.026

    Article  Google Scholar 

  9. Ge, J.; Ghassemi, A.: Stimulated reservoir volume by hydraulic fracturing in naturally fractured shale gas reservoirs. In: Paper ARMA-2012-468 Presented at the 46th U.S. Rock Mechanics/Geomechanics Symposium, Chicago, Illinois (2012)

  10. Fisher, M.K.; Wright, C.A.; Davidson, B.M.; Goodwin, A.K.; Fielder, E.O.; Buckler, W.S.; Steinsberger, N.P.: Integrating fracture mapping technologies to optimize stimulations in the barnett shale. In: Paper SPE 77441 Presented at the SPE Annual Technical Conference and Exhibition, San Antonio, Texas (2002). https://doi.org/10.2118/77441-MS

  11. Mayerhofer, M.J.; Lolon, E.P.; Youngblood, J.E.; Heinze, J.R.: Integration of microseismic-fracture-mapping results with numerical fracture network production modeling in the Barnett Shale. In: Paper SPE 102103 Presented at the SPE Annual Technical Conference and Exhibition, San Antonio, Texas, USA (2006). https://doi.org/10.2118/102103-MS

  12. Mayerhofer, M.J.; Lolon, E.; Warpinski, N.R.; Cipolla, C.L.; Walser, D.W.; Rightmire, C.M.: What is stimulated reservoir volume? SPE Prod. Oper. 25(01), 89–98 (2010). https://doi.org/10.2118/119890-PA

    Article  Google Scholar 

  13. Maxwell, S.C.; Urbancic, T.I.; Steinsberger, N.; Zinno, R.: Microseismic imaging of hydraulic fracture complexity in the Barnett Shale. In: Paper SPE 77440 Presented at the SPE Annual Technical Conference and Exhibition, San Antonio, Texas (2002). https://doi.org/10.2118/77440-MS

  14. Fisher, M.K.; Wright, C.A.; Davidson, B.M.; Steinsberger, N.P.; Buckler, W.S.; Goodwin, A.; Fielder, E.O.: Integrating fracture mapping technologies to improve stimulations in the Barnett shale. SPE Prod. Facil. 20(02), 85–93 (2005). https://doi.org/10.2118/77441-pa

    Article  Google Scholar 

  15. Griffin, L.G.; Wright, C.A.; Demetrius, S.L.; Blackburn, B.D.; Price, D.G.: Identification and implications of induced hydraulic fractures in waterfloods: case history HGEU. In: Paper SPE 59525 Presented at the SPE Permian Basin Oil and Gas Recovery Conference, Midland, Texas (2000). https://doi.org/10.2118/59525-MS

  16. Astakhov, D.; Roadarmel, W.; Nanayakkara, A.: A new method of characterizing the stimulated reservoir volume using tiltmeter-based surface microdeformation measurements. In: Paper SPE 151017 Presented at the SPE Hydraulic Fracturing Technology Conference, The Woodlands, Texas, USA (2012). https://doi.org/10.2118/151017-MS

  17. Yu, G.; Aguilera, R.: 3D analytical modeling of hydraulic fracturing stimulated reservoir volume. In: Paper SPE 153486 Presented at the SPE Latin America and Caribbean Petroleum Engineering Conference, Mexico City, Mexico (2012). https://doi.org/10.2118/153486-MS

  18. Maulianda, B.T.; Hareland, G.; Chen, S.: Geomechanical consideration in stimulated reservoir volume dimension models prediction during multi-stage hydraulic fractures in horizontal wells—Glauconite tight formation in Hoadley field. In: Paper ARMA 2014-7449 Presented at the 48th U.S. Rock Mechanics/Geomechanics Symposium, Minneapolis, Minnesota (2014)

  19. Rogers, S.; Elmo, D.; Dunphy, R.; Bearinger, D.: Understanding hydraulic fracture geometry and interactions in the Horn River Basin through DFN and numerical modeling. In: Paper SPE 137488 Presented at the Canadian Unconventional Resources and International Petroleum Conference, Calgary, Alberta, Canada (2010). https://doi.org/10.2118/137488-MS

  20. Meyer, B.R.; Bazan, L.W.: A discrete fracture network model for hydraulically induced fractures—theory, parametric and case studies. In: Paper SPE 140514 Presented at the SPE Hydraulic Fracturing Technology Conference, The Woodlands, Texas, USA (2011). https://doi.org/10.2118/140514-MS

  21. Weng, X.; Kresse, O.; Cohen, C.-E.; Wu, R.; Gu, H.: Modeling of hydraulic fracture network propagation in a naturally fractured formation. SPE Prod. Oper. 26(04), 368–380 (2011). https://doi.org/10.2118/140253-pa

    Article  Google Scholar 

  22. McClure, M.; Horne, R.N.: Discrete Fracture Network Modeling of Hydraulic Stimulation: Coupling Flow and Geomechanics. Springer, Berlin (2013)

    Book  Google Scholar 

  23. Huang, J.; Safari, R.; Lakshminarayanan, S.; Mutlu, U.; McClure, M.: Impact of discrete fracture network (DFN) reactivation on productive stimulated rock volume: microseismic, geomechanics and reservoir coupling. In: Paper ARMA 2014-7017 Presented at the 48th U.S. Rock Mechanics/Geomechanics Symposium, Minneapolis, Minnesota (2014)

  24. Sun, Y.: Impact of Slickwater Fracturing Fluid Compositions on the Petrophysical Properties of Shale and Tightsand. Missouri University of Science and Technology, Rolla (2014)

    Google Scholar 

  25. Economides, M.J.; Nolte, K.G.; Ahmed, U.; Schlumberger, D.: Reservoir Stimulation, vol. 18. Wiley, Chichester (2000)

    Google Scholar 

  26. England, A.; Green, A.: Some Two-Dimensional Punch and Crack Problems in Classical Elasticity, vol. 59. Cambridge University Press, Cambridge (1963)

    MATH  Google Scholar 

  27. Guo, J.; Lu, Q.; Zhu, H.; Wang, Y.; Ma, L.: Perforating cluster space optimization method of horizontal well multi-stage fracturing in extremely thick unconventional gas reservoir. J. Nat. Gas Sci. Eng. 26, 1648–1662 (2015). https://doi.org/10.1016/j.jngse.2015.02.014

    Article  Google Scholar 

  28. Liu, C.; Liu, H.; Zhang, Y.; Deng, D.; Wu, H.: Optimal spacing of staged fracturing in horizontal shale-gas well. J. Petrol. Sci. Eng. 132, 86–93 (2015). https://doi.org/10.1016/j.petrol.2015.05.011

    Article  Google Scholar 

  29. Guo, D.; Ji, L.; Zhao, J.; Liu, C.: 3-D fracture propagation simulation and production prediction in coalbed. Appl. Math. Mech. 22(4), 385–393 (2001). https://doi.org/10.1023/a:1016337331556

    Article  MATH  Google Scholar 

  30. Elbel, J.L.; Piggott, A.R.; Mack, M.G.: Numerical modeling of multilayer fracture treatments. In: Paper SPE 23982 Presented at the Permian Basin Oil and Gas Recovery Conference, Midland, Texas (1992). https://doi.org/10.2118/23982-MS

  31. Crouch, S.: Solution of plane elasticity problems by the displacement discontinuity method. I. Infinite body solution. Int. J. Numer. Methods Eng. 10(2), 301–343 (1976). https://doi.org/10.1002/nme.1620100206

    Article  MathSciNet  MATH  Google Scholar 

  32. Cheng, Y.: Boundary element analysis of the stress distribution around multiple fractures: implications for the spacing of perforation clusters of hydraulically fractured horizontal wells. In: Paper SPE 125769 Presented at the SPE Eastern Regional Meeting, Charleston, West Virginia, USA (2009). https://doi.org/10.2118/125769-MS

  33. Wu, K.; Olson, J.E.: Investigation of the impact of fracture spacing and fluid properties for interfering simultaneously or sequentially generated hydraulic fractures. SPE Prod. Oper. 28(04), 427–436 (2013). https://doi.org/10.2118/163821-pa

    Article  Google Scholar 

  34. Schepers, K.C.; Gonzalez, R.J.; Koperna, G.J.; Oudinot, A.Y.: Reservoir modeling in support of shale gas exploration. In: Paper SPE 123057 Presented at the Latin American and Caribbean Petroleum Engineering Conference, Cartagena de Indias, Colombia (2009). https://doi.org/10.2118/123057-MS

  35. Du, C.M.; Zhang, X.; Zhan, L.; Gu, H.; Hay, B.; Tushingham, K.; Ma, Y.Z.: Modeling hydraulic fracturing induced fracture networks in shale gas reservoirs as a dual porosity system. In: Paper SPE 132180 Presented at the International Oil and Gas Conference and Exhibition in China, Beijing, China (2010). https://doi.org/10.2118/132180-MS

  36. Ozkan, E.; Raghavan, R.: New solutions for well test analysis problems: part 1-analytical considerations. SPE Form. Eval. 6(03), 359–368 (1991). https://doi.org/10.2118/18615-pa

    Article  Google Scholar 

  37. Stehfest, H.: Algorithm 368: numerical inversion of laplace transforms. Commun. ACM 13(1), 47–49 (1970). https://doi.org/10.1145/361953.361969

    Article  Google Scholar 

  38. Warpinski, N.R.: Hydraulic fracturing in tight, fissured media. J. Petrol. Technol. 43(02), 146–209 (1991). https://doi.org/10.2118/20154-pa

    Article  Google Scholar 

  39. Ren, L.; Lin, R.; Zhao, J.; Yang, K.; Hu, Y.; Wang, X.: Simultaneous hydraulic fracturing of ultra-low permeability sandstone reservoirs in China: mechanism and its field test. J. Cent. South Univ. 22(4), 1427–1436 (2015). https://doi.org/10.1007/s11771-015-2660-1

    Article  Google Scholar 

  40. Warpinski, N.R.; Teufel, L.W.: Influence of geologic discontinuities on hydraulic fracture propagation. J. Petrol. Technol. 39(02), 209–220 (1987). https://doi.org/10.2118/13224-pa

    Article  Google Scholar 

  41. Guo, T.; Li, J.; Lao, M.; Li, W.: Integrated geophysical technologies for unconventional reservoirs and case study within fuling shale gas field, Sichuan Basin, China. In: Paper SPE 178531 Presented at the Unconventional Resources Technology Conference, San Antonio, Texas, USA (2015). https://doi.org/10.2118/178531-MS

  42. Zhao, J.; Li, Z.; Hu, Y.; Ren, L.; Tao, Z.: The impacts of microcosmic flow in nanoscale shale matrix pores on the gas production of a hydraulically fractured shale-gas well. J. Nat. Gas Sci. Eng. 29(Supplement C), 431–439 (2016). https://doi.org/10.1016/j.jngse.2016.01.025

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to acknowledge the financial support of the Major Program of the National Natural Science Foundation of China (51490653), National Natural Science Foundation of China (51404204), and the National Science and Technology Major Project of the Ministry of Science and Technology of China (2016ZX05023005-001-002).

Author information

Authors and Affiliations

  1. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, 610500, China

    Lan Ren, Ran Lin & Jinzhou Zhao

Authors
  1. Lan Ren
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ran Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jinzhou Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ran Lin.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ren, L., Lin, R. & Zhao, J. Stimulated Reservoir Volume Estimation and Analysis of Hydraulic Fracturing in Shale Gas Reservoir. Arab J Sci Eng 43, 6429–6444 (2018). https://doi.org/10.1007/s13369-018-3208-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13369-018-3208-0

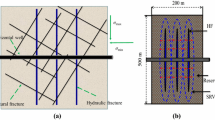
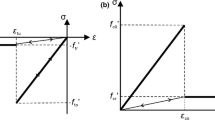
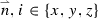
Keywords

Search

Navigation