Skip to main content

Advertisement

SpringerLink
Log in

Optimal Configuration of the Metro Rail Transit Station Service Facilities by Integrated Simulation-Optimization Method Using Passengers’ Flow Fluctuation

  • Research Article - Civil Engineering
  • Published:
Arabian Journal for Science and Engineering Aims and scope Submit manuscript

Abstract

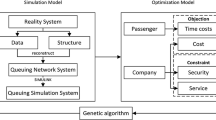
This paper proposes an integrated discrete-event simulation (DES) using phase-type (PH) distribution and optimization method for the performance assessment, as well as optimal configuration of metro rail transit (MRT) station service facilities. The MRT facilities (including ticket facilities and elevator) are represented as a queuing network system with the passengers’ arrival flow and the service time based on the PH distribution, which considers the flow and service time fluctuation. The necessary performance measures include facility utilization, mean number of passengers and waiting time of passengers in the facilities are obtained by PH-based DES model of service facilities. The model is then coupled with a genetic algorithm that works simultaneously to give the optimal configuration of service facilities. The results of PH-based DES model are first verified by existing PH-based analytical models and then compared with other existing exponential-based and deterministic-based queuing models. The results reveal that increase in squared coefficient of variation of arrival interval causes an increase in the performance measure values and high number of ticket facilities compared to existing models. The existing models therefore underestimate the results. The squared coefficient of variation is an important parameter and cannot be ignored in analysis and design of service facilities. This research provides a more realistic and novel PH-based DES, as well as PH-based simulation-optimization method that will assist the planners and designers of MRT stations to make intelligent decisions regarding analysis and design.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

i :

Number of facility

\(\lambda _{a,i} \) :

Passengers’ arrival rate to the ith facility

E[X]:

Passengers’ arrival interval

\(\varepsilon \) :

Peak-hour factor

\(c_{a,i}^2 \) :

Squared coefficient of variation of arrival interval of the ith facility

\(\mu _{s,i} \) :

Mean service rate of the ith facility

\(c_{s,i}^2 \) :

Squared coefficient of variation of service time of the ith facility

c :

Number of servers in each facility

q :

Peak-hour volume (ped/h)

1F:

Ground floor

− 1F:

Lower ground floor

\(\alpha \) :

Sub-stochastic vector for the passengers’ arrival process

D:

Sub-generator matrix for the passengers’ arrival process

\(\beta \) :

Sub-stochastic vector for service process of the service facility

H:

Sub-generator matrix for service process of the service facility

\(\rho \) :

Utilization of the facility

\(E{[{N}_{q}]}\) :

Mean number of passengers in the queue of the facility

\(E{[{W}_{q}]}\) :

Mean waiting time of passengers in the queue of the facility

n :

Number of passengers in the facility

f :

Degree of Erlang Distribution

U :

Uniformly distributed random number

References

  1. Kittelson Associates; USFT Administration; TCR Program; TD Corporation; NRCTR Board: Transit Capacity and Quality of Service Manual. Transportation Research Board of the National Academies (2003)

  2. Shi, Z.H.; Zhou, Q.R.; Zheng, X.W.: Code for design of metro, Beijing Urban Construction, Design Research Institute, Ministry of Construction of People’s Republic of China (2003)

  3. Jiang, Y.; Hu, L.; Lu, G.: Determined method of subway footway width based on queuing theory. J. Traffic Transp. Eng. 10, 61–67 (2010)

    Google Scholar 

  4. Cheah, J.; Smith, J.M.: Generalized M/G/C/C state dependent queueing models and pedestrian traffic flows. Queueing Syst. 15(1–4), 365–386 (1994)

    Article  MATH  Google Scholar 

  5. Chen, S.K.; Liu, S.; Xiaom, X.: M/G/C/C-based model of passenger evacuation capacity of stairs and corridors in urban rail transit station. J. China Railw. Soc. 34, 7–12 (2012)

    Google Scholar 

  6. Cruz, F.R.B.; Smith, J.M.; Queiroz, D.C.: Service and capacity allocation in M/G/C/C state-dependent queueing networks. Comput. Oper. Res. 32(6), 1545–1563 (2005)

    Article  MATH  Google Scholar 

  7. Smith, J.M.G.: State-dependent queueing models in emergency evacuation networks. Transp. Res. Part B Methodol. 25(6), 373–389 (1991)

    Article  Google Scholar 

  8. Mitchell, D.H.; MacGregor Smith, J.: Topological network design of pedestrian networks. Transp. Res. Part B Methodol. 35(2), 107–135 (2001)

    Article  Google Scholar 

  9. Xu, X.; Liu, J.; Li, H.; Hu, J.: Analysis of subway station capacity with the use of queueing theory. Transp. Res. Part C Emerg. Technol. 38, 28–43 (2014)

    Article  Google Scholar 

  10. Yuhaski, S.J.; Smith, J.M.: Modeling circulation systems in buildings using state dependent queueing models. Queueing Syst. 4(4), 319–338 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  11. Hu, L.; Jiang, Y.; Zhu, J.; Chen, Y.: A PH/PH state-dependent queuing model for metro station corridor width design. Eur. J. Oper. Res. 240(1), 109–126 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  12. Krishnamoorthy, A.; Babu, S.; Narayanan, V.C.: MAP/(PH/PH)/c queue with self-generation of priorities and non-preemptive service. Stoch. Anal. Appl. 26(6), 1250–1266 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  13. Miyazawa, M.; Sakuma, Y.; Yamaguchi, S.: Asymptotic behaviors of the loss probability for a finite buffer queue with QBD structure. Stoch. Models 23(1), 79–95 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  14. Alfa, A.S.; Zhao, Y.Q.: Overload analysis of the PH/PH/1/K queue and the queue of M/G/1/K type with very large K. Asian Pac. J. Oper. Res. 17, 122–136 (2000)

    MathSciNet  MATH  Google Scholar 

  15. Baumann, H.; Sandmann, W.: Numerical solution of level dependent quasi-birth-and-death processes. Proc. Comput. Sci. 1(1), 1561–1569 (2010)

    Article  Google Scholar 

  16. Løvås, G.G.: Modeling and simulation of pedestrian traffic flow. Transp. Res. Part B Methodol. 28(6), 429–443 (1994)

    Article  Google Scholar 

  17. Cruz, F.R.B.; MacGregor Smith, J.; Medeiros, R.O.: An M/G/C/C state-dependent network simulation model. Comput. Oper. Res. 32(4), 919–941 (2005)

    Article  MATH  Google Scholar 

  18. Khalid, R.; Nawawi, M.K.; Kawsar, L.A.; Ghani, N.A.; Kamil, A.A.; Mustafa, A.: A discrete event simulation model for evaluating the performances of an M/G/C/C state dependent queuing system. PLoS ONE 8(4), e58402 (2013)

    Article  Google Scholar 

  19. Jiang, Y.; Zhu, J.; Hu, L.; Lin, X.; Khattak, A.: A G/G(n)/C/C state-dependent simulation model for metro station corridor width design. J. Adv. Transp. 50, 273–295 (2016)

    Article  Google Scholar 

  20. Cetin, N.; Burri, A.; Nagel, K.: A large-scale agent-based traffic microsimulation based on queue model. In: Proceedings of Swiss Transport Research Conference (STRC), Monte Verita, CH (2003)

  21. Gomes, G.; May, A.; Horowitz, R.: Congested freeway microsimulation model using VISSIM. Transp. Res. Rec. J. Transp. Res. Board 1876, 71–81 (2004)

    Article  Google Scholar 

  22. Blue, V.J.; Adler, J.L.: Cellular automata microsimulation for modeling bi-directional pedestrian walkways. Transp. Res. Part B Methodol. 35(3), 293–312 (2001)

    Article  Google Scholar 

  23. Yang, J.; et al.: Modeling pedestrians’ road crossing behavior in traffic system micro-simulation in China. Transp. Res. Part A Policy Pract. 40(3), 280–290 (2006)

    Article  Google Scholar 

  24. Mathew, T.V.; Radhakrishnan, P.: Calibration of microsimulation models for nonlane-based heterogeneous traffic at signalized intersections. J. Urban Plan. Dev. 136(1), 59–66 (2010)

    Article  Google Scholar 

  25. Blue, V.; Adler, J.: Emergent fundamental pedestrian flows from cellular automata microsimulation. Transp. Res. Rec. J. Transp. Res. Board 1644, 29–36 (1998)

    Article  Google Scholar 

  26. Heywood, P.; Maddock, S.; Casas, J.; Garcia, D.; Brackstone, M.; Richmond, P.: Data-parallel agent-based microscopic road network simulation using graphics processing units. Simul. Model. Pract. Theory 83, 188–200 (2017)

    Article  Google Scholar 

  27. Abuamer, I.M.; Sadat, M;, Silgu, M.A.; Celikoglu, H.B.: Analyzing the effects of driver behavior within an adaptive ramp control scheme: a case-study with ALINEA. In: 2017 IEEE International Conference on Vehicular Electronics and Safety (ICVES), IEEE (pp. 109–114). (2017) https://doi.org/10.1109/ICME.2017.7991910

  28. Abuamer, I.M.; Silgu, M.A.; Celikoglu, H.B.: Micro-simulation based ramp metering on Istanbul freeways: an evaluation adopting ALINEA. In: 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), IEEE (pp. 695–700). (2016). https://doi.org/10.1109/ITSC.2016.7795629

  29. Aksoy, G.; Celikoglu, H.B.; Gedizlioglu, E.: Analysis of toll queues by micro-simulation: results from a case study in Istanbul. Proc. Soc. Behav. Sci. 111, 614–623 (2014). https://doi.org/10.1016/j.sbspro.2014.01.095

    Article  Google Scholar 

  30. ANTONIOU C, BARCELÒ J, BRACKSTONE M, CELIKOGLU H, CIUFFO B, PUNZO V, SYKES P, TOLEDO T, VORTISCH P, WAGNER P, PUNZO V, BRACKSTONE M (2014) vol. JRC885. Publications Office of the European Union. https://doi.org/10.2788/12197

  31. Sadat, M.; Celikoglu, H.B.: Simulation-based variable speed limit systems modelling: an overview and a case study on Istanbul freeways. Transp. Res. Proc. 22, 607–614 (2017). https://doi.org/10.1016/j.trpro.2017.03.051

    Article  Google Scholar 

  32. Khattak, A.; Yangsheng, J.; Lu, H.; Juanxiu, Z.: Modeling and simulation of metro transit station walkway as a state-dependent queuing system based on the phase-type distribution. Int. J. Traffic Transp. Eng. 5(5), 103–111 (2016)

    Google Scholar 

  33. Khattak, A.; Yangsheng, J.: Modeling of subway stations circulation facilities as state-dependent queuing network based on phase-type distribution. In: IEEE International Conference on Intelligent Transportation Engineering (ICITE) IEEE, pp. 133–138 (2016)

  34. Khattak, A.; Yangsheng, J.; Lu, H.; Juanxiu, Z.: Width design of urban rail transit station walkway: a novel simulation-based optimization approach. Urban Rail Transit 3(2), 112–127 (2017)

    Article  Google Scholar 

  35. Khattak, A.; Jiang, Y.; Zhu, J.; Hu, L.: A new simulation-optimization approach for the circulation facilities design at urban rail transit station. Arch. Transp. 43, 3 (2017)

    Google Scholar 

  36. Fishman, G.: Discrete-Event Simulation: Modeling, Programming, and Analysis. Springer, Berlin (2013)

    MATH  Google Scholar 

  37. Jiang, Y.; Lin, X.: Simulation and optimization of the ticket vending machine configuration in metro stations based on anylogic software. In: Fourth International Conference on Transportation Engineering, pp. 754–760 (2013)

  38. Hassannayebi, E.; Sajedinejad, A.; Mardani, S.: Urban rail transit planning using a two-stage simulation-based optimization approach. Simul. Model. Pract. Theory 49, 151–166 (2014)

    Article  Google Scholar 

  39. Figueira, G.; Almada-Lobo, B.: Hybrid simulation-optimization methods: a taxonomy and discussion. Simul. Model. Pract. Theory 46, 118–134 (2014)

    Article  Google Scholar 

  40. Hagendorf, O.; Pawletta, T.; Larek, R.: An approach for simulation-based parameter and structure optimization of MATLAB/Simulink models using evolutionary algorithms. Simulation 89, 1115 (2013)

    Article  Google Scholar 

  41. Swisher, J.R.; Hyden, P.D.; Jacobson, S.H.; Schruben, L.W.: Simulation optimization: a survey of simulation optimization techniques and procedures. In: Proceedings of the 32nd Conference on Winter Simulation, Society for Computer Simulation International, Orlando, Florida, pp. 119–128 (2000)

  42. Fu, M.C.: Feature article: optimization for simulation: theory vs practice. INFORMS J. Comput. 14(3), 192–215 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  43. Messac, A.: Optimization in Practice with MATLAB. Cambridge University Press, Cambridge (2015)

    Book  MATH  Google Scholar 

  44. Hubscher-Younger, T.; Mosterman, P.J.; DeLand, S.; Orqueda, O.; Eastman, D.: Integrating discrete-event and time-based models with optimization for resource allocation. In: Proceedings of Simulation Conference (WSC), Proceedings of the 2012 Winter, pp. 1–15 (2012)

  45. Nguyen, A.T.; Reiter, S.; Rigo, P.: A review on simulation-based optimization methods applied to building performance analysis. Appl. Energy 113, 1043–1058 (2014)

    Article  Google Scholar 

  46. Neuts, M.F.: Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach. Dover Publications, Mineola (1981)

    MATH  Google Scholar 

  47. Sadre, R.: Decomposition-Based Analysis of Queueing Networks. University of Twente, Twente (2007)

    Google Scholar 

  48. Sadre, R.; Haverkort, B.: Decomposition-based queueing network analysis with FiFi queues. In: Boucherie, R.J., van Dijk, N.M. (eds.) Queueing Netw., pp. 643–699. Springer, New York (2011)

    Chapter  Google Scholar 

  49. Liao, Y.-J.; Liao, G.-X.; Lo, S.-M.: Influencing factor analysis of ultra-tall building elevator evacuation. Proc. Eng. 71, 583–590 (2014)

    Article  Google Scholar 

  50. Smith, J.M.; Tan, B.: Handbook of Stochastic Models and Analysis of Manufacturing System Operations. Springer, Berlin (2013)

    Book  MATH  Google Scholar 

  51. Jiang, Y.; Khattak, A.; Hu, L.; Zhu, J.; Yao, Z.: Analytical modeling of two-level urban rail transit station elevator system as phase-type bulk service queuing system. European Transport-TRASPORTI EUROPEI, p. 62 (2016)

  52. Ying, H.; Fengjin, Y.; ShouWen, J.: Queuing theory based simulation and optimization of ticket office. In: 2014 IEEE Workshop on Proceedings of Advanced Research and Technology in Industry Applications (WARTIA), pp. 1217–1219

Download references

Acknowledgements

We would like to express our sincere acknowledgement to National Natural Science Foundation of China (Serial Nos. 51578465 and 71402149), Basic Research Project of Sichuan Province, the Chinese government for the funding of doctoral program at Southwest Jiaotong University and the colleagues of National United Engineering Laboratory of Integrated and Intelligent Transportation at Southwest Jiaotong University, Chengdu for their support and valuable advices.

Author information

Authors and Affiliations

  1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu, Sichuan, China

    Afaq Khattak & Jiang Yangsheng

  2. Department of Civil Engineering, International Islamic University, Islamabad, Pakistan

    Afaq Khattak & Malik Muneeb Abid

Authors
  1. Afaq Khattak
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jiang Yangsheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Malik Muneeb Abid
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Afaq Khattak.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khattak, A., Yangsheng, J. & Abid, M.M. Optimal Configuration of the Metro Rail Transit Station Service Facilities by Integrated Simulation-Optimization Method Using Passengers’ Flow Fluctuation. Arab J Sci Eng 43, 5499–5516 (2018). https://doi.org/10.1007/s13369-018-3194-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13369-018-3194-2

Keywords

Search

Navigation