Channel surfaces in Lie sphere geometry

Abstract

We discuss channel surfaces in the context of Lie sphere geometry and characterise them as certain $\Omega _{0}$-surfaces. Since $\Omega _{0}$-surfaces possess a rich transformation theory, we study the behaviour of channel surfaces under these transformations. Furthermore, by using certain Dupin cyclide congruences, we characterise Ribaucour pairs of channel surfaces.

1 Introduction

Channel surfaces, that is, envelopes of one-parameter families of spheres, have been intensively studied for many years. Although these surfaces are a classical notion (e.g., Blaschke 1929; Lie 1872; Monge 1850), they are also a subject of interest in recent research. For example, in Bernstein (2001), Hertrich-Jeromin (2003), Hertrich-Jeromin et al. (2001), Jensen et al. (2016) and Musso and Nicolodi (1999, 2002) channel surfaces were studied in the context of Möbius geometry and in Musso and Nicolodi (1995) and Peternell and Pottmann (1998) they were given a Laguerre geometric treatment. Furthermore, the subclasses of channel linear Weingarten surfaces (Hertrich-Jeromin et al. 2015) and Willmore channel surfaces (Musso and Nicolodi 1999) were recently discussed. Moreover, a novel application of channel surfaces to semi-discrete curvature line nets was explored in Burstall et al. (2017). Channel surfaces are also widely used in Computer Aided Geometric Design and the existence of a rational parametrisation was investigated in Peternell and Pottmann (1997).

In this paper, we discuss various aspects of channel surfaces in the context of Lie sphere geometry. Following the example of Blaschke (1929) and more recently (Jensen et al. 2016), we exploit the hexaspherical coordinate model introduced by Lie (1872). In Sect. 3, by applying the gauge theoretic approach of Burstall et al. (2018), Clarke (2012) and Pember (2018), we show that Legendre immersions parametrising channel surfaces are $\Omega _{0}$-surfaces that admit linear conserved quantities. Furthermore, we obtain the somewhat surprising result that $\Omega _{0}$-surfaces possessing a polynomial conserved quantity are channel surfaces. In Musso and Nicolodi (2006) it was shown that $\Omega _{0}$-surfaces are deformable surfaces in Lie sphere geometry. This induces a transformation of $\Omega _{0}$-surfaces called the Calapso transformation. We prove that this transformation preserves the class of channel surfaces.

In Sect. 4 we characterise Ribaucour pairs of umbilic-free Legendre immersions in terms of a special pair of Dupin cyclide congruences enveloping both surfaces. We investigate the behaviour of these Dupin cyclide congruences when both Legendre immersions participating in this Ribaucour pair parametrise channel surfaces. In a similar vein, given a pair of sphere curves, we construct two 1-parameter families of Dupin cyclides whose coincidence determines when the envelopes of the sphere curves form a Ribaucour pair (with corresponding circular curvature lines). We then consider the Lie-Darboux transformation of $\Omega _{0}$-surfaces, a particular Ribaucour transformation. We show that any Lie-Darboux transform of a channel surface is again a channel surface. Furthermore, any Ribaucour pair of channel surfaces (with corresponding circular curvature lines) can be arranged as a Lie-Darboux pair.

In Sect. 5 we apply our theory of channel surfaces to the special case of curves in conformal geometry. We recover a result of Burstall and Hertrich-Jeromin (2006), showing how the classical notion of Ribaucour transforms of curves is related to the Ribaucour transforms of Legendre immersions parametrising these curves.

2 Preliminaries

Given a vector space V and a manifold $\Sigma$, we shall denote by $\underline{V}$ the trivial bundle $\Sigma \times V$. Given a vector subbundle W of $\underline{V}$, we define the derived bundle of W, denoted $W^{(1)}$, to be the subset of $\underline{V}$ consisting of the images of sections of W and derivatives of sections of W with respect to the trivial connection on $\underline{V}$. In this paper, most of the derived bundles that appear will be vector subbundles of the trivial bundle, but in general this is not always the case as, for example, the rank of the derived bundle may not be constant over $\Sigma$.

Throughout this paper we shall be considering the pseudo-Euclidean space ${\mathbb {R}}^{4,2}$, i.e., a 6-dimensional vector space equipped with a non-degenerate symmetric bilinear form $(\,,\,)$ of signature (4, 2). Let ${\mathcal {L}}$ denote the lightcone of ${\mathbb {R}}^{4,2}$. According to Lie’s (1872) correspondence, points in the projective lightcone ${\mathbb {P}}({\mathcal {L}})$ correspond to spheres in any three dimensional space form. A detailed modern account of this is given in Cecil (2008). Given a manifold $\Sigma$ we then have that any smooth map $s:\Sigma \rightarrow {\mathbb {P}}({\mathcal {L}})$ corresponds to a sphere congruence in any space form. We shall thus refer to s as a sphere congruence. Such a map can also be identified as a smooth rank 1 null subbundle of the trivial bundle $\underline{{\mathbb {R}}}^{4,2}$.

The orthogonal group $\text {O}(4,2)$ acts transitively on ${\mathcal {L}}$ and thus acts transitively on ${\mathbb {P}}({\mathcal {L}})$. In Cecil (2008) it is shown that $\text {O}(4,2)$ is a double cover for the group of Lie sphere transformations. The Lie algebra $\mathfrak {o}(4,2)$ of $\text {O}(4,2)$ is well known to be isomorphic to the exterior algebra $\wedge ^{2}{\mathbb {R}}^{4,2}$ via the identification

$$\begin{aligned} a\wedge b\, (c) = (a,c)b - (b,c)a, \end{aligned}$$

for $a,b,c\in {\mathbb {R}}^{4,2}$. We shall frequently use this fact throughout this paper.

Given a manifold $\Sigma$, we define the following product of two vector-valued 1-forms $\omega _{1},\omega _{2}\in \Omega ^{1}(\underline{{\mathbb {R}}}^{4,2})$:

$$\begin{aligned} \omega _{1}\curlywedge \omega _{2}(X,Y) := \omega _{1}(X)\wedge \omega _{2}(Y) - \omega _{1}(Y)\wedge \omega _{2}(X), \end{aligned}$$

for $X,Y\in \Gamma T\Sigma$. Hence, $\omega _{1}\curlywedge \omega _{2}$ is a 2-form taking values in $\wedge ^{2}\underline{{\mathbb {R}}}^{4,2}$. Notice that $\omega _{1}\curlywedge \omega _{2} = \omega _{2}\curlywedge \omega _{1}$.

Recall that we also have the following product for two $\mathfrak {so}(4,2)$-valued 1-forms $A,B\in \Omega ^{1}(\mathfrak {so}(4,2))$:

$$\begin{aligned}{}[A\wedge B](X,Y) = [A(X),B(Y)]-[A(Y),B(X)], \end{aligned}$$

for $X,Y\in \Gamma T\Sigma$.

2.1 Legendre maps

Let ${\mathcal {Z}}$ denote the Grassmannian of isotropic 2-dimensional subspaces of ${\mathbb {R}}^{4,2}$. Suppose that $\Sigma$ is a 2-dimensional manifold and let $f:\Sigma \rightarrow {\mathcal {Z}}$ be a smooth map. By viewing f as a 2-dimensional subbundle of the trivial bundle $\underline{{\mathbb {R}}}^{4,2}$, we may define a tensor, analogous to the solder form defined in Burstall and Calderbank (2004) and Burstall and Rawnsley (1990),

$$\begin{aligned} \beta : T\Sigma \rightarrow Hom(f,f^{(1)}/f),\quad X\mapsto (\sigma \mapsto d_{X}\sigma \, mod\, f). \end{aligned}$$

In accordance with (Cecil 2008, Theorem 4.3) we have the following definition:

Definition 2.1

A map $f:\Sigma \rightarrow {\mathcal {Z}}$ is a Legendre map if it satisfies the contact condition, $f^{(1)}\le f^{\perp }$, and the immersion condition, $\ker \beta =\{0\}$.

Remark 2.2

The contact and immersion conditions together imply that $f^{(1)}=f^{\perp }$ (see Pinkall 1985).

Note that $f^{\perp }/f$ is a rank 2 subbundle of $\underline{{\mathbb {R}}}^{4,2}/f$ that inherits a positive definite metric from ${\mathbb {R}}^{4,2}$.

Definition 2.3

Let $p\in \Sigma$. Then a 1-dimensional subspace $s(p)\le f(p)$ is a curvature sphere of f at p if there exists a non-zero subspace $T_{s(p)}\le T_{p}\Sigma$ such that $\beta (T_{s(p)})s(p) = 0$. We call the maximal such $T_{s(p)}$ the curvature space of s(p).

It was shown in Pinkall (1985) that at each point p there is either one or two curvature spheres. We say that p is an umbilic point of f if there is exactly one curvature sphere s(p) at p and in that case $T_{s(p)}=T_{p}\Sigma$.

Away from umbilic points we have that the curvature spheres form two rank 1 subbundles $s_{1},s_{2}\le f$ with respective curvature subbundles $T_{1}=\bigcup _{p\in \Sigma }T_{s_{1}(p)}$ and $T_{2}=\bigcup _{p\in \Sigma }T_{s_{2}(p)}$. We then have that $f=s_{1}\oplus s_{2}$ and $T\Sigma = T_{1}\oplus T_{2}$. A conformal structure c is induced on $T\Sigma$ as the set of all indefinite metrics whose null lines are $T_{1}$ and $T_{2}$. This conformal structure induces a Hodge-star operator $\star$ that acts as id on $T^{*}_{1}$ and $-id$ on $T^{*}_{2}$.

Suppose that f is umbilic-free. Then for each curvature subbundle $T_{i}$ we may define a rank 3 subbundle $f_{i}\le f^{\perp }$ as the set of sections of f and derivatives of sections of f along $T_{i}$. One can check that given any non-zero section $\sigma \in \Gamma f$ such that $\langle \sigma \rangle \cap s_{i} = \{0\}$ we have that

$$\begin{aligned} f_{i} = f\oplus d\sigma (T_{i}). \end{aligned}$$

Furthermore,

$$\begin{aligned} f^{\perp }/f = f_{1}/f\oplus _{\perp } f_{2}/f, \end{aligned}$$

and each $f_{i}/f$ inherits a positive definite metric from that of ${\mathbb {R}}^{4,2}$.

Lemma 2.4

Let $X\in \Gamma T_{1}$ and $Y\in \Gamma T_{2}$ be nowhere zero. Then for any sections $\sigma ,\tilde{\sigma }\in \Gamma f$, $(d_{X}\sigma , d_{X}\tilde{\sigma })=0$ (or, $(d_{Y}\sigma , d_{Y}\tilde{\sigma })=0$) if and only if either $\sigma \in \Gamma s_{1}$ or $\tilde{\sigma }\in \Gamma s_{1}$ (respectively, $\sigma \in \Gamma s_{2}$ or $\tilde{\sigma }\in \Gamma s_{2}$).

Proof

Let $\sigma _{1}\in \Gamma s_{1}$ and $\sigma _{2}\in \Gamma s_{2}$ be lifts of the curvature sphere congruences. Then we may write $\sigma = \alpha \sigma _{1} + \beta \sigma _{2}$ and $\tilde{\sigma } = \gamma \sigma _{1} + \delta \sigma _{2}$, for some smooth functions $\alpha , \beta , \gamma ,\delta$. Then

$$\begin{aligned} (d_{X}\sigma , d_{X}\tilde{\sigma }) = \beta \delta (d_{X}\sigma _{2}, d_{X}\sigma _{2}), \end{aligned}$$

since $d_{X}\sigma _{1}\in \Gamma f$. Since $f_{2}/f$ inherits a positive definite metric from ${\mathbb {R}}^{4,2}$, we have that $(d_{X}\sigma _{2}, d_{X}\sigma _{2})$ is nowhere zero. Thus, $(d_{X}\sigma , d_{X}\tilde{\sigma })=0$ if and only if $\beta =0$ or $\delta =0$, i.e., $\sigma \in \Gamma s_{1}$ or $\tilde{\sigma }_{1}\in \Gamma s_{1}$. $\square$

2.2 Dupin cyclides

After spheres, Dupin cyclides are the next simplest object in Lie sphere geometry. One constructs them as follows: let D be a 3-dimensional subspace of ${\mathbb {R}}^{4,2}$ which inherits an inner product of signature (2, 1) from ${\mathbb {R}}^{4,2}$. Then we have a splitting of ${\mathbb {R}}^{4,2}$ as

$$\begin{aligned} {\mathbb {R}}^{4,2} = D\oplus D^{\perp }. \end{aligned}$$

One may then regularly parametrise the projective lightcones of D and $D^{\perp }$ by maps $L: S^{1}\rightarrow {\mathbb {P}}(D)$ and $L^{\perp }:S^{1}\rightarrow {\mathbb {P}}(D^{\perp })$. Then one obtains a Legendre map

$$\begin{aligned} {\mathcal {X}}:S^{1}\times S^{1}\rightarrow {\mathcal {Z}}, \quad {\mathcal {X}}(u,v)= L(u)\oplus L^{\perp }(v). \end{aligned}$$

The projection of ${\mathcal {X}}$ to any space form yields a parametrisation of a Dupin cyclide. Moreover, L and $L^{\perp }$ are the curvature sphere congruences of ${\mathcal {X}}$.

Dupin cyclides were originally defined by Dupin (1822) as the envelope of a 1-parameter family of spheres tangent to three given spheres. In this way a Dupin cyclide is determined by these three spheres. This can be seen by letting $a,b,c\in {\mathbb {P}}({\mathcal {L}})$ such that their span has signature (2, 1). Then letting $D=a\oplus b \oplus c$, one can construct a Dupin cyclide as above. Furthermore, a, b and c belong to one family of curvature spheres of the resulting Dupin cyclide and every curvature sphere in the other family is simultaneously tangent to a, b and c.

Now suppose that $f:\Sigma \rightarrow {\mathcal {Z}}$ is an umbilic-free Legendre map with curvature sphere congruences $s_{1}$ and $s_{2}$ and respective curvature subbundles $T_{1}$ and $T_{2}$. Let $\sigma _{1}\in \Gamma s_{1}$ and $\sigma _{2}\in \Gamma s_{2}$ be lifts of the curvature sphere congruences and let $X\in \Gamma T_{1}$ and $Y\in \Gamma T_{2}$. Then from Definition 2.3 it follows immediately that

$$\begin{aligned} d_{X}\sigma _{1},d_{Y}\sigma _{2}\in \Gamma f. \end{aligned}$$

Let

$$\begin{aligned} S_{1}:= \left\langle \sigma _{1},d_{Y}\sigma _{1},d_{Y}d_{Y}\sigma _{1}\right\rangle \quad \text {and}\quad S_{2}:= \left\langle \sigma _{2},d_{X}\sigma _{2},d_{X}d_{X}\sigma _{2}\right\rangle . \end{aligned}$$

It was shown in Blaschke (1929) that $S_{1}$ and $S_{2}$ are orthogonal rank 3 subbundles of $\underline{{\mathbb {R}}}^{4,2}$ and the restriction of the metric on ${\mathbb {R}}^{4,2}$ to each $S_{i}$ has signature (2, 1). Furthermore, $S_{1}$ and $S_{2}$ do not depend on choices and we have the following orthogonal splitting

$$\begin{aligned} \underline{{\mathbb {R}}}^{4,2} = S_{1}\oplus _{\perp } S_{2} \end{aligned}$$

of the trivial bundle. We refer to this splitting as the Lie cyclide splitting of $\underline{{\mathbb {R}}}^{4,2}$ because it can be identified with the Lie cyclides of f, i.e., a special congruence of Dupin cyclides making second order contact with f (see Blaschke 1929, Sect. 86).

This splitting now yields a splitting of the trivial connection d on $\underline{{\mathbb {R}}}^{4,2}$:

$$\begin{aligned} d = {\mathcal {D}} + {\mathcal {N}}, \end{aligned}$$

where ${\mathcal {D}}$ is the direct sum of the induced connections on $S_{1}$ and $S_{2}$ and

$$\begin{aligned} {\mathcal {N}} = d - {\mathcal {D}}\in \Omega ^{1}((Hom(S_{1},S_{2})\oplus Hom(S_{2},S_{1}))\cap \mathfrak {o}(4,2)). \end{aligned}$$

(1)

Since $S_{1}$ and $S_{2}$ are orthogonal, we have that ${\mathcal {D}}$ is a metric connection on $\underline{{\mathbb {R}}}^{4,2}$ and ${\mathcal {N}}$ is a skew-symmetric endomorphism. Hence, ${\mathcal {N}}\in \Omega ^{1}(S_{1}\wedge S_{2})$.

3 Channel surfaces in Lie sphere geometry

Channel surfaces have been a rich area of interest for many years. Examples of such surfaces include surfaces of revolution, tubular surfaces and Dupin cyclides. They are given simply by the following well-known definition:

Definition 3.1

A channel surface is the envelope of a 1-parameter family of spheres.

There are several characterisations of these surfaces, for example, in Euclidean geometry they are the surfaces for which one family of curvature lines are circular or, equivalently, one of the principal curvatures is constant along the corresponding family of curvature lines, i.e., in terms of local curvature line coordinates (u, v), $\kappa _{1,u}=0$ or $\kappa _{2,v}=0$. To begin with, we shall recall some facts about channel surfaces (cf. Blaschke 1929; Jensen et al. 2016) in the Lie geometric setup.

A sphere curve can be realised as a map $s:I\rightarrow {\mathbb {P}}({\mathcal {L}})$, where I is a 1-dimensional manifold. We impose a regularity condition that ensures the existence of an envelope of s: the induced metric on $s^{(1)}/s$ is positive definite. We now seek a parametrisation of the envelope of this sphere curve. In order to do this we shall construct a Legendre map enveloping s. Firstly, let V be a rank 3 subbundle of $I\times {\mathbb {R}}^{4,2}$ such that the induced metric on V has signature (2, 1) and such that $s^{(1)}\le V$. Then $V^{\perp }$ is a rank 3 subbundle of $I\times {\mathbb {R}}^{4,2}$ and at each point $t\in I$ we may parametrise the projective light cone of $V^{\perp }$ by a map $\tilde{s}_{t}:S^{1}\rightarrow {\mathbb {P}}({\mathcal {L}})$. Without loss of generality, we make the assumption that this is a regular parametrisation, i.e., the induced metric on $\tilde{s}_{t}^{(1)}/\tilde{s}_{t}$ is positive definite. We may extend this smoothly to all of I to obtain a map

$$\begin{aligned} \tilde{s}:I\times S^{1}\rightarrow {\mathbb {P}}({\mathcal {L}}). \end{aligned}$$

We also extend the maps s and V trivially to maps on $I\times S^{1}$.

Lemma 3.2

$f:=s\oplus \tilde{s}$ is a Legendre map.

Proof

Since $s\le V$ and $\tilde{s}\le V^{\perp }$ we have that $f:=s\oplus \tilde{s}$ is a map from $I\times S^{1}$ into ${\mathcal {Z}}$. Furthermore, $s^{(1)}\le V\perp \tilde{s}$. Hence, f satisfies the contact condition. The immersion condition follows from the regularity conditions of s on I and $\tilde{s}_{t}$ on $S^{1}$ for each $t\in I$. $\square$

Remark 3.3

Suppose that $f=s\oplus \tilde{s}$ is a Legendre map arising from V. Suppose that $\overline{V}$ is another rank 3 subbundle of $I\times {\mathbb {R}}^{4,2}$ such that the induced metric on $\overline{V}$ has signature (2, 1) and such that $s^{(1)}\le \overline{V}$. Then

$$\begin{aligned} \bar{s}:=f\cap \overline{V}^{\perp }:I\times S^{1}\rightarrow {\mathbb {P}}({\mathcal {L}}) \end{aligned}$$

is well-defined, and since $\overline{V}$ only depends on I, $\bar{s}(t,.)$ parametrises the projective lightcone of $\overline{V}_{t}^{\perp }$, for each $t\in I$.

Since s only depends on I, one has that s is a curvature sphere congruence of f with curvature subbundle $T_{1}:= TS^{1}$. If one chooses $V = \langle \sigma , d_{Y}\sigma ,d_{Y}d_{Y}\sigma \rangle$, where $\sigma \in \Gamma s$ and $Y\in \Gamma TI$, then the resulting $\tilde{s}$ will be the other curvature sphere congruence of f with curvature subbundle $T_{2}:= TI$: this follows from the fact that for any lifts $\sigma \in \Gamma s$ and $\tilde{\sigma }\in \Gamma \tilde{s}$,

$$\begin{aligned} 0= (d_{Y}d_{Y}\sigma , \tilde{\sigma })= - (d_{Y}\sigma , d_{Y}\tilde{\sigma }). \end{aligned}$$

Then by Lemma 2.4, one has that either $\sigma \in \Gamma s_{2}$ or $\tilde{\sigma }\in \Gamma s_{2}$. However, our assumption that $s^{(1)}/s$ is positive definite means that $\tilde{\sigma }\in \Gamma s_{2}$. In this case, the splitting of the trivial bundle $\underline{{\mathbb {R}}}^{4,2}=V\oplus V^{\perp }$ is the Lie cyclide splitting of f.

Conversely, suppose that $f:\Sigma \rightarrow {\mathcal {Z}}$ is an umbilic-free Legendre map such that one of the curvature sphere congruence $s_{i}$ is constant along the leaves of its curvature subbundle $T_{i}$, i.e., $d_{X}\sigma _{i}\in \Gamma s_{i}$ for $\sigma _{i}\in \Gamma s_{i}$ and $X\in \Gamma T_{i}$. Then f envelopes a sphere congruence $s:=s_{i}$ that only depends on one parameter. Hence, f parametrises a channel surface.

Proposition 3.4

An umbilic-free Legendre map $f:\Sigma \rightarrow {\mathcal {Z}}$ parametrises a channel surface if and only if one of the curvature sphere congruences $s_{i}$ is constant along the leaves of its curvature subbundle $T_{i}$.

In view of Proposition 3.4 we have the following definition:

Definition 3.5

$T_{i}$ is called a circular curvature direction of f if $s_{i}$ is constant along the leaves of $T_{i}$.

Since the Lie cyclides of a Legendre map are given by

$$\begin{aligned} S_{1}=\langle \sigma _{1}, d_{Y}\sigma _{1}, d_{Y}d_{Y}\sigma _{1}\rangle \quad \text {and}\quad S_{2}=\langle \sigma _{2}, d_{X}\sigma _{2}, d_{X}d_{X}\sigma _{2}\rangle , \end{aligned}$$

where $\sigma _{1}\in \Gamma s_{1}$, $\sigma _{2}\in \Gamma s_{2}$, $X\in \Gamma T_{1}$ and $Y\in \Gamma T_{2}$, one deduces the following corollary:

Corollary 3.6

An umbilic-free Legendre map $f:\Sigma \rightarrow {\mathcal {Z}}$ parametrises a channel surface if and only if the Lie cyclides of f are constant along the leaves of one of the curvature subbundles $T_{i}$, i.e., ${\mathcal {N}}(T_{i}) = 0$.

3.1 Channel surfaces as $\Omega _{0}$-surfaces

In Musso and Nicolodi (2006) a class of surfaces, called Lie applicable surfaces, are shown to be the only surfaces in Lie sphere geometry that admit second order deformations. It is shown that this class of surfaces naturally splits into two subclasses, $\Omega$-surfaces and $\Omega _{0}$-surfaces. This is the Lie sphere geometric analogue of R- and $R_{0}$-surfaces in projective geometry. Although $\Omega _{0}$-surfaces are objects of Lie sphere geometry, they were classically defined (Demoulin 1911a, b, c) as those surfaces in space forms which satisfy

$$\begin{aligned} \left( \frac{V}{U}\frac{\sqrt{E}}{\sqrt{G}}\frac{\kappa _{1,u}}{\kappa _{1}-\kappa _{2}}\right) _{v} =0 \quad \text {or}\quad \left( \frac{U}{V}\frac{\sqrt{G}}{\sqrt{E}}\frac{\kappa _{2,v}}{\kappa _{1}-\kappa _{2}}\right) _{u}=0 , \end{aligned}$$

(2)

for some functions U of u and V of v, in terms of curvature line coordinates (u, v), where E and G denote the usual coefficients of the first fundamental form and $\kappa _{1}$ and $\kappa _{2}$ denote the principal curvatures. Since channel surfaces in space forms are those that satisfy either $\kappa _{1,u}=0$ or $\kappa _{2,v}=0$, it is immediate that these surfaces are $\Omega _{0}$-surfaces and in fact any choice of functions U and V will satisfy (2).

We shall use the following gauge-theoretic definition of $\Omega _{0}$-surfaces:

Definition 3.7

(Pember 2018, Definition 3.1) A Legendre map $f:\Sigma \rightarrow {\mathcal {Z}}$ is an $\Omega _{0}$-surface if there exists a closed 1-form $\eta \in \Omega ^{1}(f\wedge f^{\perp })$ such that $[\eta \wedge \eta ]=0$ and

$$\begin{aligned} q(X,Y)= tr (\sigma \mapsto \eta (X)d_{Y}\sigma :f\rightarrow f) \end{aligned}$$

is a non-zero degenerate quadratic differential.

In fact, given a closed 1-form $\eta \in \Omega ^{1}(f\wedge f^{\perp })$, one obtains a family of such closed 1-forms called the gauge orbit of $\eta$ by defining $\tilde{\eta }:= \eta - d\tau$, for any $\tau \in \Gamma (\wedge ^{2}f)$. Furthermore, the quadratic differential is well defined on this gauge orbit, i.e., $\tilde{q}=q$, where $\tilde{q}$ denotes the quadratic differential of $\tilde{\eta }$. It was shown in Pember (2018) that for $\Omega _{0}$-surfaces there exists a special member of this gauge orbit called the middle potential satisfying $\eta \in \Omega ^{1}(s_{i}\wedge f^{\perp })$ for one of the curvature sphere congruences $s_{i}$, namely,

$$\begin{aligned} \eta = \sigma _{i}\wedge \star d\sigma _{i} \end{aligned}$$

for some lift $\sigma _{i}\in \Gamma s_{i}$. In this case we say that $s_{i}$ is an isothermic curvature sphere congruence.

Now suppose that a Legendre map f parametrises a channel surface. Then by Proposition 3.4 one of the curvature spheres, say $s_{1}$, is constant along the leaves of $T_{1}$. We may choose a lift $\sigma _{1}$ of $s_{1}$ so that $d|_{T_{1}}\sigma _{1} =0$. Such a lift is determined up to multiplication by a function $\mu :\Sigma \rightarrow {\mathbb {R}}$ such that $d|_{T_{1}}\mu =0$. Now consider $d(\star d\sigma _{1})$. If we let $X\in \Gamma T_{1}$ and $Y\in \Gamma T_{2}$, then

$$\begin{aligned} d(\star d\sigma _{1})(X,Y)&= d_{X}(\star d_{Y}\sigma _{1}) - d_{Y}(\star d_{X}\sigma _{1}) - \star d_{[X,Y]}\sigma _{1}\\&= -d_{X}d_{Y}\sigma _{1} - d_{Y}d_{X}\sigma _{1} - d_{\star [X,Y]}\sigma _{1}\\&= - 2d_{Y}d_{X}\sigma _{1} - d_{[X,Y] + \star [X,Y]}\sigma _{1}\\&= 0, \end{aligned}$$

since $d|_{T_{1}}\sigma _{1} =0$ and $[X,Y] + \star [X,Y] \in \Gamma T_{1}$. Hence, $d(\star d\sigma _{1})=0$. This implies that the $f\wedge f^{\perp }$ valued 1-form

$$\begin{aligned} \eta = \sigma _{1}\wedge \star d\sigma _{1} \end{aligned}$$

(3)

is closed. Since $\eta (T_{1})=0$, it follows trivially that $[\eta \wedge \eta ]=0$. Furthermore, the quadratic differential

$$\begin{aligned} q(X,Y) = tr(\sigma \mapsto \eta (X)d_{Y}\sigma ) = - (\star d_{X}\sigma _{1},d_{Y}\sigma _{1}), \end{aligned}$$

is non-zero, taking values in $(T^{*}_{2})^{2}$. Hence, f is an $\Omega _{0}$-surface.

In summary, we have seen in two different ways that:

Proposition 3.8

Channel surfaces are $\Omega _{0}$-surfaces.

Given a function $\mu :\Sigma \rightarrow {\mathbb {R}}$ such that $d|_{T_{1}}\mu =0$, by defining $\tilde{\sigma }_{1}=\mu \sigma _{1}$ we have that

$$\begin{aligned} \tilde{\eta } = \tilde{\sigma }_{1}\wedge \star d\tilde{\sigma }_{1} \end{aligned}$$

is a closed 1-form with values in $f\wedge f^{\perp }$. We then have that the quadratic differential $\tilde{q}$ satisfies $\tilde{q}=\mu ^{2} q$. Therefore, since the quadratic differentials do not coincide we have that $\eta$ and $\tilde{\eta }$ do not belong to the same gauge orbit.

It is well known that $\Omega _{0}$-surfaces, and more generally Lie applicable surfaces, constitute an integrable system, stemming from the presence of a 1-parameter family of flat connections:

Lemma 3.9

(Clarke 2012, Lemma 4.2.6) Suppose that $\eta \in \Omega ^{1}(f\wedge f^{\perp })$ is closed and $[\eta \wedge \eta ]=0$. Then $\{d+t\eta \}_{t\in {\mathbb {R}}}$ is a 1-parameter family of flat connections.

It was shown in Burstall et al. (2018) that one may distinguish subclasses of surfaces amongst $\Omega$-surfaces by using polynomial conserved quantities of the aforementioned family of flat connections. Furthermore, it was shown in Burstall et al. (2012) that $\Omega _{0}$-surfaces possessing a constant conserved quantity project to tubular surfaces in certain space forms. We shall now investigate general polynomial conserved quantities of $\Omega _{0}$-surfaces. Firstly, let us recall the definition of a polynomial conserved quantity:

Definition 3.10

A non-zero polynomial $p = p(t)\in \Gamma \underline{{\mathbb {R}}}^{4,2}[t]$ is called a polynomial conserved quantity of $\{d+t\eta \}_{t\in {\mathbb {R}}}$ if p(t) is a parallel section of $d+t\eta$ for all $t\in {\mathbb {R}}$.

It was shown in Burstall et al. (2018, Lemma 3.2) that if $\{d+t\eta \}_{t\in {\mathbb {R}}}$ admits a polynomial conserved quantity, then for any other member $\tilde{\eta }$ in the gauge orbit of $\eta$, $\{d+t\tilde{\eta }\}_{t\in {\mathbb {R}}}$ admits a polynomial conserved quantity.

The following theorem shows that we may distinguish channel surfaces from general $\Omega _{0}$-surfaces by the presence of a polynomial conserved quantity:

Theorem 3.11

Channel surfaces admit gauge orbits with linear conserved quantities. On the other hand, any $\Omega _{0}$-surface with a polynomial conserved quantity is a channel surface.

Proof

Suppose that $f=s_{1}\oplus s_{2}$ is a channel surface with $s_{1}$ constant along the leaves of $T_{1}$. Let $\sigma _{1}\in \Gamma s_{1}$ be a lift of $s_{1}$ such that $d|_{T_{1}}\sigma _{1} = 0$ and let $\mathfrak {p}$ be a non-zero vector in ${\mathbb {R}}^{4,2}$. Then the lift $\tilde{\sigma }_{1}:=- \frac{1}{(\sigma _{1},\mathfrak {p})}\sigma _{1}$ satisfies $d|_{T_{1}}\tilde{\sigma }_{1}=0$ and $(\tilde{\sigma }_{1}, \mathfrak {p})=-1$. Now if we let $\tilde{\eta }:= \tilde{\sigma }_{1}\wedge \star d\tilde{\sigma }_{1}$ then $\tilde{\eta }$ is closed and $\mathfrak {p}+t\tilde{\sigma }_{1}$ is a linear conserved quantity of $d+t\tilde{\eta }$.

Now suppose that f is an $\Omega _{0}$-surface with a closed 1-form $\eta = \sigma _{1}\wedge \star d\sigma _{1}$. Suppose further that $d+t\eta$ admits a polynomial conserved quantity $p(t)= p_{0}+ t p_{1} + ... + t^{d}p_{d}$ with $p_{d}\ne 0$. For a contradiction, let us assume that f is not a channel surface. This implies that $s_{1}^{(1)}= f\oplus d\sigma _{1}(T_{2})$. Now,

$$\begin{aligned} 0=\eta p_{d}= (\sigma _{1}\wedge \star d\sigma _{1}) p_{d} = (\sigma _{1}, p_{d}) \star d\sigma _{1} - (\star d\sigma _{1}, p_{d}) \sigma _{1}. \end{aligned}$$

Thus, $(\sigma _{1}, p_{d})=0$ and $(\star d\sigma _{1}, p_{d})=0$. Hence, $p_{d}\in \Gamma (s_{1}^{(1)})^{\perp }$. Thus, we may write

$$\begin{aligned} p_{d} = a\, \sigma _{1} + b\, \sigma _{2} + c\, d_{X}\sigma _{2}, \end{aligned}$$

where $\sigma _{2}\in \Gamma s_{2}$ and $X\in \Gamma T_{1}$. Since $dp_{d} = -\eta p_{d-1}$, one has that $dp_{d}\in \Omega ^{1}(s_{1}^{(1)})$. This implies that

$$\begin{aligned} 0 = d_{X}p_{d}\, mod\, s_{1}^{(1)} = d_{X}c\, d_{X}\sigma _{2} + c\, d_{X}d_{X}\sigma _{2} + b\, d_{X}\sigma _{2}\, mod\, s_{1}^{(1)}. \end{aligned}$$

Since $d_{X}\sigma _{2}$ and $d_{X}d_{X}\sigma _{2}$ are linearly independent, one has that $c=b=0$. Now,

$$\begin{aligned} a \, d\sigma _{1} \, mod\, s_{1} = - (\sigma _{1},p_{d-1}) \star d\sigma _{1}\, mod\, s_{1}. \end{aligned}$$

This can only hold if $a = (\sigma _{1},p_{d-1}) =0$, which contradicts that $p_{d}\ne 0$. $\square$

3.2 Calapso transforms of channel surfaces

As previously mentioned, $\Omega _{0}$-surfaces have a rich transformation theory. One transformation that arises for these surfaces is the Calapso transformation. Suppose that $\eta \in \Omega ^{1}(f\wedge f^{\perp })$ is closed and $[\eta \wedge \eta ]=0$. Let $\{d+t\eta \}_{t\in {\mathbb {R}}}$ be the resulting 1-parameter family of flat connections. For each $t\in {\mathbb {R}}$, there exists a local orthogonal trivialising gauge transformation $T(t):\Sigma \rightarrow \text {O}(4,2)$, that is,

$$\begin{aligned} T(t)\cdot (d+t\eta ) = d. \end{aligned}$$

Definition 3.12

$f^{t}:=T(t)f$ is called a Calapso transform of f.

In Pember (2018) it was shown that $f^{t}$ is again a Lie applicable surface whose quadratic differential satisfies $q^{t}=q$. Furthermore, the curvature spheres of $f^{t}$ are given by $s_{1}^{t} = T(t)s_{1}$ and $s_{2}^{t}= T(t)s_{2}$ with respective curvature subbundles $T_{1}^{t}=T_{1}$ and $T_{2}^{t}=T_{2}$.

Suppose that f is a channel surface and, without loss of generality, suppose that $T_{1}$ is the circular curvature direction of f. Then the closed 1-form $\eta \in \Omega ^{1}(f\wedge f^{\perp })$ constructed in (3) satisfies $\eta (T_{1})=0$. Now if $\sigma ^{t}_{1}\in \Gamma s_{1}^{t}$, then $\sigma ^{t}_{1} = T(t)\sigma _{1}$, for some $\sigma _{1}\in \Gamma s_{1}$. Hence, for $X\in \Gamma T_{1}$,

$$\begin{aligned} d_{X}\sigma ^{t}_{1} = T(t)(d_{X}+ t\eta (X))\sigma _{1} = T(t)d_{X}\sigma _{1}\in \Gamma s^{t}_{1}, \end{aligned}$$

since $d_{X}\sigma _{1}\in \Gamma s_{1}$. Therefore, $s_{1}^{t}$ is constant along the leaves of $T_{1}$ and thus $f^{t}$ is a channel surface with circular direction $T_{1}$.

Theorem 3.13

The Calapso transforms of channel surfaces are channel surfaces with the same circular curvature direction.

4 Ribaucour transforms of channel surfaces

Blaschke (1929) proved that the Ribaucour transforms of a channel surface have one family of spherical curvature lines. In this section we consider the Ribaucour transforms of channel surfaces that are again channel surfaces. To begin with we recall some facts about the Ribaucour transformation and associate to each Ribaucour pair of surfaces a novel pair of Dupin cyclide congruences.

4.1 Ribaucour transforms

Suppose that $f,\hat{f}:\Sigma \rightarrow {\mathcal {Z}}$ are pointwise distinct Legendre immersions enveloping a common sphere congruence $s_{0}:=f\cap \hat{f}$. Assume that f and $\hat{f}$ are umbilic-free with respective curvature sphere congruences $s_{1},s_{2}$ and $\hat{s}_{1},\hat{s}_{2}$, and let $T_{1},T_{2}\le T\Sigma$ and $\hat{T}_{1}, \hat{T}_{2}\le T\Sigma$ denote their respective rank 1 curvature subbundles. Classically two surfaces are Ribaucour transforms of each other if they are the envelopes of a sphere congruence such that the curvature directions of the surfaces are preserved. Interpreting this in the context of umbilic-free Legendre maps we have the following definition:

Definition 4.1

Two umbilic-free Legendre maps $f,\hat{f}:\Sigma \rightarrow {\mathcal {Z}}$ are Ribaucour transforms of each other if f and $\hat{f}$ envelope a common sphere congruence $s_{0}$ and $\hat{T}_{1} = T_{1}$ and $\hat{T}_{2} = T_{2}$. We then say that f and $\hat{f}$ are a Ribaucour pair.

In Burstall and Hertrich-Jeromin (2006), the condition that two Legendre maps be Ribaucour transforms of each other was equated to the flatness of a certain normal bundle. In Pember (2018, Corollary 2.11, Remark 2.12) this definition was shown to be equivalent to the following:

Lemma 4.2

f and $\hat{f}$ are Ribaucour transforms of each other if and only if for any sphere congruences $s\le f$ and $\hat{s}\le \hat{f}$ such that $s_{0}\cap s = s_{0}\cap \hat{s}=\{0\}$ one may choose lifts $\sigma \in \Gamma s$ and $\hat{\sigma }\in \Gamma \hat{s}$ such that $d\sigma ,d\hat{\sigma }\in \Omega ^{1}((s\oplus \hat{s})^{\perp })$.

We now show that a Ribaucour pair is equipped with a special pair of Dupin cyclide congruences.

Proposition 4.3

Suppose that $s_{0}$ nowhere coincides with the curvature sphere congruences $s_{1},s_{2}$ and $\hat{s}_{1},\hat{s}_{2}$ of f and $\hat{f}$, respectively. Then f and $\hat{f}$ are Ribaucour transforms of each other if and only if

$$\begin{aligned} d\hat{\sigma }_{1}(\hat{T}_{2})\le s_{1}\oplus \hat{s}_{1}\oplus d\sigma _{1}(T_{2}) \quad \text {and}\quad d\hat{\sigma }_{2}(\hat{T}_{1})\le s_{2}\oplus \hat{s}_{2}\oplus d\sigma _{2}(T_{1}), \end{aligned}$$

(4)

where $\sigma _{i}\in \Gamma s_{i}$ and $\hat{\sigma }_{i}\in \Gamma \hat{s}_{i}$.

Proof

Suppose that f and $\hat{f}$ are Ribaucour transforms of each other and thus $\hat{T}_{1}=T_{1}$ and $\hat{T}_{2}=T_{2}$. Then $d_{X}\sigma _{1}\in \Gamma f$ and $d_{X}\hat{\sigma }_{1}\in \Gamma \hat{f}$, for $X\in \Gamma T_{1}$, $\sigma _{1}\in \Gamma s_{1}$ and $\hat{\sigma }_{1}\in \Gamma \hat{s}_{1}$. One then deduces that

$$\begin{aligned} s_{1}\oplus \hat{s}_{1}\oplus d\sigma _{1}(T_{2}) = s_{1}\oplus \hat{s}_{1}\oplus d\hat{\sigma }_{1}(T_{2}) = \langle \sigma _{0}, d_{X}\sigma _{0}, d_{X}d_{X}\sigma _{0}\rangle ^{\perp }, \end{aligned}$$

for $\sigma _{0}\in \Gamma s_{0}$. Similarly, one has that

$$\begin{aligned} s_{2}\oplus \hat{s}_{2}\oplus d\sigma _{2}(T_{1}) = s_{2}\oplus \hat{s}_{2}\oplus d\hat{\sigma }_{2}(T_{1}) = \langle \sigma _{0}, d_{Y}\sigma _{0}, d_{Y}d_{Y}\sigma _{0}\rangle ^{\perp }, \end{aligned}$$

for $Y\in \Gamma T_{2}$.

Conversely, suppose that (4) holds. Now for $\sigma _{0}\in \Gamma s_{0}$ and $X\in \Gamma T_{1}$, one has that $d_{X}\sigma _{0}\perp s_{1}\oplus \hat{s}_{1}\oplus d\sigma _{1}(T_{2})$. Thus, $0= (d_{X}\sigma _{0}, d_{\hat{Y}}\hat{\sigma }_{1})$, for any $\hat{\sigma }_{1}\in \Gamma \hat{s}_{1}$ and $\hat{Y}\in \Gamma \hat{T}_{2}$. Writing $X= \hat{X}+\mu \hat{Y}$, for some $\hat{X}\in \Gamma \hat{T}_{1}$ and smooth function $\mu$, one has that

$$\begin{aligned} 0 = (d_{\hat{X}}\sigma _{0}, d_{\hat{Y}}\hat{\sigma }_{1}) + \mu (d_{\hat{Y}}\sigma _{0}, d_{\hat{Y}}\hat{\sigma }_{1}) = \mu (d_{\hat{Y}}\sigma _{0}, d_{\hat{Y}}\hat{\sigma }_{1}), \end{aligned}$$

since $d_{\hat{X}}\hat{\sigma }_{1}\in \Gamma \hat{f}$. By Lemma 2.4, $(d_{\hat{Y}}\sigma _{0}, d_{\hat{Y}}\hat{\sigma }_{1})\ne 0$, and thus $\mu =0$. Hence, $\hat{T}_{1} = T_{1}$. A similar argument shows that $\hat{T}_{2}=T_{2}$. Hence, f and $\hat{f}$ are Ribaucour transforms of each other. $\square$

We now seek a geometric interpretation of the conditions in (4). Suppose that (u, v) are local curvature line coordinates of f about a point $p=(u_{0},v_{0})$ and consider the Dupin cyclide for which $s_{1}(u_{0},v_{0})$, $s_{1}(u_{0},v_{0}+\epsilon )$ and $\hat{s}_{1}(u_{0},v_{0})$ are contained in one family of curvature spheres, for sufficiently small $\epsilon \ne 0$. One obtains a Dupin cyclide $D_{1}(p)$ by taking the limit as $\epsilon$ tends to zero. In this way one obtains a smooth congruence $D_{1}$ of Dupin cyclides over $\Sigma$ and in fact this is represented as

$$\begin{aligned} D_{1} = s_{1}\oplus \hat{s}_{1}\oplus d\sigma _{1}(T_{2}). \end{aligned}$$

On the other hand, suppose that $(\hat{u},\hat{v})$ are curvature line coordinates for $\hat{f}$ around $p=(\hat{u}_{0},\hat{v}_{0})$. One can consider the Dupin cyclide $\hat{D}_{1}(\hat{u}_{0},\hat{v}_{0})$ formed by taking the limit $s_{1}(\hat{u}_{0},\hat{v}_{0})$, $\hat{s}_{1}(\hat{u}_{0},\hat{v}_{0})$ and $\hat{s}_{1}(\hat{u}_{0},\hat{v}_{0}+\epsilon )$ as $\epsilon$ tends to zero. We then obtain a second smooth congruence $\hat{D}_{1}$ of Dupin cyclides over $\Sigma$:

$$\begin{aligned} \hat{D}_{1} = s_{1}\oplus \hat{s}_{1}\oplus d\hat{\sigma }_{1}(\hat{T}_{2}). \end{aligned}$$

One then deduces that the first condition of (4) is equivalent to asking that the two Dupin cyclide congruences $D_{1}$ and $\hat{D}_{1}$ coincide. The second condition of (4) can be interpreted in terms of $s_{2}$ and $\hat{s}_{2}$ in an analogous way.

Therefore, if f and $\hat{f}$ are a Ribaucour pair of umbilic-free Legendre immersions, one obtains two special Dupin cyclide congruences enveloping f and $\hat{f}$:

Definition 4.4

The Dupin cyclide congruences

$$\begin{aligned} D_{1} := s_{1}\oplus \hat{s}_{1}\oplus d\sigma _{1}(T_{2}) = s_{1}\oplus \hat{s}_{1}\oplus d\hat{\sigma }_{1}(T_{2}) \end{aligned}$$

and

$$\begin{aligned} D_{2} := s_{2}\oplus \hat{s}_{2}\oplus d\sigma _{2}(T_{1}) = s_{2}\oplus \hat{s}_{2}\oplus d\hat{\sigma }_{2}(T_{1}) \end{aligned}$$

will be called the Ribaucour cyclide congruences of the Ribaucour pair f and $\hat{f}$.

As shown in the proof of Proposition 4.3, one has that

$$\begin{aligned} D_{1}^{\perp } = \langle \sigma _{0}, d_{X}\sigma _{0}, d_{X}d_{X}\sigma _{0}\rangle \quad \text {and}\quad D_{2}^{\perp } = \langle \sigma _{0}, d_{Y}\sigma _{0}, d_{Y}d_{Y}\sigma _{0}\rangle , \end{aligned}$$

where $\sigma _{0}\in \Gamma s_{0}$, $X\in \Gamma T_{1}$ and $Y\in \Gamma T_{2}$.

4.2 Ribaucour transforms of channel surfaces

We now focus on the case of Ribaucour transforms between channel surfaces. Firstly, we characterise when a Ribaucour pair consists of channel surfaces in terms of the Ribaucour cyclide congruences:

Theorem 4.5

Suppose that $f,\hat{f}:\Sigma \rightarrow {\mathcal {Z}}$ are a Ribaucour pair of umbilic-free Legendre immersions. Then f and $\hat{f}$ are channel surfaces with corresponding circular curvature direction $T_{i}$ if and only if one of the Ribaucour cyclide congruences $D_{i}$ is constant along the leaves of $T_{i}$.

Proof

Suppose that f and $\hat{f}$ are channel surfaces with corresponding circular curvature direction $T_{i}$. Without loss of generality, suppose that $i=1$. Then we may choose lifts $\sigma _{1}\in \Gamma s_{1}$ and $\hat{\sigma }_{1}\in \Gamma \hat{s}_{1}$ such that $d_{X}\sigma _{1}=d_{X}\hat{\sigma }_{1}=0$ for any $X\in \Gamma T_{1}$. Then for any $Y\in \Gamma T_{2}$,

$$\begin{aligned} d_{X}d_{Y}\sigma _{1} = d_{Y}d_{X}\sigma _{1}+ d_{[X,Y]}\sigma _{1} = d_{[X,Y]}\sigma _{1} . \end{aligned}$$

Since $d\sigma _{1}(T_{1})=0$, $d_{[X,Y]}\sigma _{1}\in \Gamma d\sigma _{1}(T_{2})$. Thus, any $\nu \in \Gamma D_{1}$ satisfies $d_{X}\nu \in \Gamma D_{1}$. Hence, $D_{1}$ is constant along the leaves of $T_{1}$.

Conversely, suppose that $D_{1}$ is constant along the leaves of $T_{1}$. Then for any lift $\sigma _{1}\in \Gamma s_{1}$, $d\sigma _{1}(T_{1})\le D_{1}$. On the other hand, $d\sigma _{1}(T_{1})\perp d\sigma _{1}(T_{2})$ and $d\sigma _{1}(T_{1})\le f^{\perp }$. Thus $d\sigma _{1}(T_{1})\le s_{1}$ and $s_{1}$ is constant along the leaves of $T_{1}$. An analogous argument shows that $\hat{s}_{1}$ is constant along the leaves of $T_{1}$, proving the result. $\square$

We now change our viewpoint and seek a characterisation of the pairs of regular sphere curves whose envelopes form a Ribaucour pair:

Theorem 4.6

Suppose that $s, \hat{s}:I\rightarrow {\mathbb {P}}({\mathcal {L}})$ are two regular sphere curves that never span a contact element, i.e., s is nowhere orthogonal to $\hat{s}$. Then the envelopes of s and $\hat{s}$ are Ribaucour transforms¹ of each other, with corresponding circular curvature directions, if and only if $s^{(1)}\oplus \hat{s}=\hat{s}^{(1)}\oplus s$.

Proof

Using the parametrisation of Sect. 3, let $f,\hat{f}:I\times S^{1}\rightarrow {\mathcal {Z}}$ be Legendre maps enveloping s and $\hat{s}$, respectively, such that f and $\hat{f}$ are Ribaucour transforms of each other. Let $s_{0}:= f\cap \hat{f}$. Assuming that the circular curvature directions of f and $\hat{f}$ correspond, one has that $s_{1}=s$ and $\hat{s}_{1}=\hat{s}$. It then follows by Proposition 4.3 that

$$\begin{aligned} s^{(1)}\oplus \hat{s} = s_{1}\oplus \hat{s}_{1}\oplus d\sigma _{1}(T_{2})= s_{1}\oplus \hat{s}_{1}\oplus d\hat{\sigma }_{1}(T_{2}) = \hat{s}^{(1)}\oplus s, \end{aligned}$$

where $T_{2}= TI$.

Conversely, suppose that $s^{(1)}\oplus \hat{s}=\hat{s}^{(1)}\oplus s=:V$. Since $V^{\perp }$ has signature (2, 1), we may at each point of I parametrise the elements of the projective lightcone along $S^{1}$, i.e., we have $s_{0}:I\times S^{1}\rightarrow V^{\perp }$. Then let $f:=s_{0}\oplus s$ and $\hat{f}:=s_{0}\oplus \hat{s}$. f and $\hat{f}$ are Legendre maps by Lemma 3.2 and are Ribaucour transforms of each other because $T_{1}=\hat{T}_{1} = TS^{1}$ and $T_{2}=\hat{T}_{2}=TI$. $\square$

We can interpret the result of Theorem 4.6 geometrically as follows. For $t\in I$ and sufficiently small non-zero $\epsilon$, s(t), $s(t+\epsilon )$ and $\hat{s}(t)$ belong to one family of curvature spheres of a Dupin cyclide. By allowing $\epsilon$ to tend to zero, we obtain a unique Dupin cyclide at t. On the other hand by repeating the same process with s(t), $\hat{s}(t)$ and $\hat{s}(t+\epsilon )$, we obtain another Dupin cyclide at t. By doing this for all $t\in I$, we obtain two 1-parameter families of Dupin cyclides. The theorem states that the envelopes of s and $\hat{s}$ are a Ribaucour pair if and only if these two families of Dupin cyclides coincide.

4.3 Darboux transforms

We shall now recall the construction of Darboux transforms of $\Omega _{0}$-surfaces.

Suppose that f is an $\Omega _{0}$-surface with isothermic curvature sphere congruence $s_{1}$. Let $\eta \in \Omega ^{1}(s_{1}\wedge f^{\perp })$ be the middle potential of f. We then have that $\{d+t\eta \}_{t\in {\mathbb {R}}}$ is a 1-parameter family of flat connections. The flatness of these connections implies that they admit many parallel sections. Suppose that $\hat{s}$ is a parallel subbundle of $d+m\eta$ for $m\in {\mathbb {R}}\backslash \{0\}$. Let $s_{0}:= f\cap \hat{s}^{\perp }$ and $\hat{f}:= s_{0}\oplus \hat{s}$. Then it was shown in Pember (2018) that $\hat{f}$ is a Legendre map and furthermore an $\Omega _{0}$-surface with isothermic curvature sphere congruence $\hat{s}$. We call $\hat{f}$ a Lie-Darboux transform of f with parameter m.

Theorem 4.7

Any Lie-Darboux transformation of a channel surface is a channel surface with the same circular curvature direction. On the other hand, given a Ribaucour pair of channel surfaces with corresponding circular curvature directions, we may choose gauge orbits so that this is a Lie-Darboux pair.

Proof

Suppose that f is a channel surface with circular direction $T_{1}$. Then, as we learned in Sect. 3.1, f is an $\Omega _{0}$-surface and for any lift $\sigma _{1}\in \Gamma s_{1}$ with $d|_{T_{1}}\sigma _{1}=0$, $\eta =\sigma _{1}\wedge \star d\sigma _{1}$ is closed. Suppose that $\hat{s}$ is a parallel subbundle of $d+m\eta$, i.e., for some $\hat{\sigma }\in \Gamma \hat{s}$, $d\hat{\sigma }=-m\eta \hat{\sigma }$. Then since f is a channel surface with circular direction $T_{1}$, one has that $\eta (T_{1})=0$. Thus, $d|_{T_{1}}\hat{\sigma }=0$. Hence, $\hat{s}$ is constant along the leaves of $T_{1}$ and thus, $\hat{f}$ is a channel surface with circular direction $T_{1}$.

Suppose now that f and $\hat{f}$ are a Ribaucour pair of channel surfaces with circular curvature direction $T_{1}$. By Lemma 4.2, since f and $\hat{f}$ are a Ribaucour pair, we may choose lifts $\sigma _{1}\in \Gamma s_{1}$ and $\hat{\sigma }_{1}\in \Gamma \hat{s}_{1}$ such that

$$\begin{aligned} d\sigma _{1}, d\hat{\sigma }_{1}\in \Omega ^{1}((s_{1}\oplus \hat{s}_{1})^{\perp }). \end{aligned}$$

Without loss of generality, we may assume that $(\sigma _{1},\hat{\sigma }_{1})=-1$. Since f and $\hat{f}$ are channel surfaces with circular direction $T_{1}$, we must also have that $d|_{T_{1}}\sigma _{1}=d|_{T_{1}}\hat{\sigma }_{1}=0$. Now let

$$\begin{aligned} \eta := \sigma _{1}\wedge d\hat{\sigma }_{1}. \end{aligned}$$

Then

$$\begin{aligned} d\eta = d\sigma _{1}\curlywedge d\hat{\sigma }_{1} = d|_{T_{1}}\sigma _{1}\curlywedge d|_{T_{2}}\hat{\sigma } +d|_{T_{2}}\sigma _{1}\curlywedge d|_{T_{1}}\hat{\sigma } =0. \end{aligned}$$

Hence, $\eta$ defines an $\Omega _{0}$-structure on f. Furthermore,

$$\begin{aligned} d\hat{\sigma }_{1} + \eta \hat{\sigma }_{1} = d\hat{\sigma }_{1} + (\sigma _{1},\hat{\sigma }_{1})d\hat{\sigma }_{1}= 0. \end{aligned}$$

Thus, $\hat{f}$ is a Lie-Darboux transform of f. $\square$

5 Ribaucour transforms of curves

In Burstall and Hertrich-Jeromin (2006) a definition of Ribaucour pairs of k-dimensional submanifolds in the conformal n-sphere is given. It is shown that for appropriately constructed Legendre lifts, two k-dimensional submanifolds are a Ribaucour pair if and only if there Legendre lifts form a Ribaucour pair. In this section, using Theorem 4.6, we quickly recover this result in the case of curves in the conformal 3-sphere. To do this, we break symmetry as explained in detail in Burstall et al. (2018), Sect. 2.2.

Let $\mathfrak {p} \in {\mathbb {R}}^{4,2}$ be a timelike vector. A curve in a conformal geometry $\langle \mathfrak {p} \rangle ^\perp$ can be interpreted as a sphere curve $s: I \rightarrow {\mathbb {P}}({\mathcal {L}})$, which takes values in $\langle \mathfrak {p} \rangle ^\perp$. By the construction of Sect. 3, one obtains a Legendre immersion parametrising this curve. Furthermore, s is one of the curvature sphere congruences of this Legendre immersion.

Conversely, suppose that f is an umbilic-free Legendre map such that one of the curvature sphere congruences, say $s_{1}$, satisfies $s_{1}\perp \mathfrak {p}$. Thus, $s_{1}=f\cap \langle \mathfrak {p}\rangle ^{\perp }$. Now $d_{X}\sigma _{1}\in \Gamma f$ for all $X\in \Gamma T_{1}$ and $\sigma _{1}\in \Gamma s_{1}$. On the other hand, $(d_{X}\sigma _{1},\mathfrak {p}) = d_{X}(\sigma _{1},\mathfrak {p})=0$, and thus $d_{X}\sigma _{1} \in \Gamma s_{1}$. Thus, $s_{1}$ is constant along the leaves of $T_{1}$ and projects to a curve in the conformal geometry of $\langle \mathfrak {p}\rangle ^{\perp }$. We have thus arrived at the following proposition:

Proposition 5.1

An umbilic-free Legendre map parametrises a regular curve in the conformal geometry $\langle \mathfrak {p}\rangle ^{\perp }$ if and only if one of the curvature sphere congruences $s_{i}$ satisfies $s_{i}\perp \mathfrak {p}$.

We now recall the definition of Ribaucour transforms of curves:

Definition 5.2

(Burstall et al. 2016; Hertrich-Jeromin 2003) Two curves form a Ribaucour pair if they envelop a circle congruence.

Theorem 5.3

Two non-intersecting regular curves are Ribaucour transforms of each other if and only if there exists a Ribaucour pair of Legendre maps parametrising these curves with corresponding circular curvature directions.

Proof

Let $s,\hat{s}:I\rightarrow {\mathbb {P}}({\mathcal {L}})$ be the corresponding curves in $\langle \mathfrak {p}\rangle ^{\perp }$. By Theorem 4.6, there exists a Ribaucour pair of Legendre maps parametrising s and $\hat{s}$ with corresponding circular curvature directions if and only if $s^{(1)}\oplus \hat{s} = \hat{s}^{(1)}\oplus s$. However, $s^{(1)}\oplus \hat{s}$ and $\hat{s}^{(1)}\oplus s$ both belong to the conformal geometry $\langle \mathfrak {p}\rangle ^{\perp }$, and the condition $s^{(1)}\oplus \hat{s} = \hat{s}^{(1)}\oplus s$ is exactly the condition that s and $\hat{s}$ envelope a circle congruence (see, Burstall et al. 2016). In fact, the projective lightcone of $s^{(1)}\oplus \hat{s} = \hat{s}^{(1)}\oplus s$ yields exactly this circle congruence. $\square$

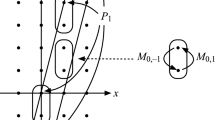
We may interpret Theorem 5.3 in Euclidean geometry as follows: two curves are Ribaucour transforms of each other if and only if tubes of the same radius over these curves are Ribaucour transforms of each other with corresponding circular curvature directions. We shall illustrate this with the following simple example. This example is generated by taking a Ribaucour transform of a straight line. By performing a parallel transformation, one obtains a Ribaucour transform of a cylinder. An explicit parametrisation of this Ribaucour transform is given in Tenenblat (2002). The tangent circles between the Ribaucour pair of curves become tori with the same radii as that of the tubular surfaces. These tori form the Ribaucour cyclide congruence that only depends on one parameter (see Theorem 4.5). Furthermore, the black circles in Fig. 1 illustrate how the circular curvature lines on the cylinder and its Ribaucour transform coincide with circular curvature lines on the enveloping tori.

Fig. 1

Ribaucour transform of a straight line and, after parallel transformation, Ribaucour transform of a cylinder

Remark 5.4

Theorem 4.7 applied to the particular case of curves recovers a result given in Burstall et al. (2016): for any Ribaucour pair of curves we can choose a polarization such that it becomes a Darboux pair.

In light of this section, we may reinterpret Theorem 4.6 in the following way. Using isotropy projection [see for example Blaschke (1929) and Cecil (2008)], one may view spheres as points in ${\mathbb {R}}^{3,1}$. Thus, sphere curves correspond to curves in ${\mathbb {R}}^{3,1}$. One may also view ${\mathbb {R}}^{4,2}$ as the conformal compactification of ${\mathbb {R}}^{3,1}$. The condition $s^{(1)}\oplus \hat{s} = \hat{s}^{(1)}\oplus s$ is then equivalent to the corresponding curves in ${\mathbb {R}}^{3,1}$ being Ribaucour transforms of each other.