Skip to main content
SpringerLink
Log in

Numerical analysis of chemical reaction and non-linear radiation for magneto-cross nanofluid over a stretching cylinder

  • Original Article
  • Published:
Applied Nanoscience Aims and scope Submit manuscript

Abstract

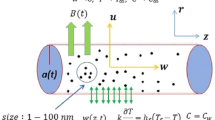
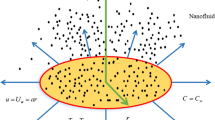
This work is focused on the numerical solution of non-Newtonian unsteady flow of a Cross nanofluid over a continuously expanding/contracting horizontal cylinder. The flow study and joule heating are obtainable in the presence of a binary chemical reaction, radiation and nanofluid for a devised Nanomaterial model, considering the phenomena of Brownian motion and thermophoresis. The idea of Boussinesq-approximations is developed with the help of momentum, temperature and concentration equations by using appropriate transformations. The nonlinear partial differential equations (PDE’s) are converted to ordinary ones via appropriate transformations. A numerical solution is obtained through the implementation of a boundary value problem fourth-order (bvp4c) technique. Flow parameters are discussed graphically. Physical engineering quantities, like surface drag forces, Nusselt and Sherwood numbers are examined numerically. It is concluded that heat transfer rates are enhanced for heat source/sink and Brownian motion.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig 2
Fig 3
Fig 4
Fig 5
Fig 6
Fig 7

Similar content being viewed by others

Abbreviations

\(u,v\) :

Velocity components

\(r,x\) :

Cylindrical coordinates

\(\rho\) :

Fluid density

\(D_{{\text{B}}}\) :

Brownian diffusion coefficient

\(\delta\) :

Chemical reaction parameter

\(a,c\) :

Constants

\(\Gamma\) :

Material parameter

\(\tau_{{\text{w}}}\) :

Surface shear stress

\(D_{{\text{T}}}\) :

Thermophoresis diffusion coefficient

\(N_{{\text{b}}}\) :

Brownian motion parameter

\(T_{{\text{w}}}\) :

Surface temperature

\(T_{\infty }\) :

Ambient fluid temperature

\(n\) :

Power law index

\(\mu\) :

Dynamic viscosity

\(\theta\) :

Dimensionless temperature

\(c_{{\uprho }}\) :

Specific heat

\(u_{w} \left( {x,t} \right)\) :

Stretching velocity

\(C_{\infty }\) :

Ambient nanoparticle concentration

\(q_{{\text{w}}}\) :

Wall heat flux

\(\mu_{\infty }\) :

Infinite shear viscosity

\(C_{{\text{f}}}\) :

Skin friction coefficient

\(k_{c}\) :

Rate of chemical reaction

\({\text{Sh}}\) :

Sherwood number

\(Q_{0}\) :

Heat generation/absorption coefficient

\(\sigma^{*}\) :

Stefan Boltzmann

\(\alpha\) :

Thermal diffusivity

\(q_{{\text{r}}}\) :

Radiative heat flux

\(q_{{\text{w}}}\) :

Wall heat flux

\(\eta\) :

Dimensionless variable

\(\psi\) :

Stream function

\({\text{We}}\) :

Local Weissenberg number

\({\Pr}\) :

Prandtl number

\(T\) :

Temperature of fluid

\(C\) :

Nanoparticles concentration

\(M\) :

Magnetic parameter

\({\text{Sc}}\) :

Schmidt number

\(\gamma\) :

Curvature parameter

\(\beta\) :

Heat generation/absorption parameter

\(\theta_{{\text{w}}}\) :

Temperature ratio parameter

\(N_{{\text{t}}}\) :

Thermophoresis parameter

\(N_{{\text{R}}}\) :

Radiation parameter

\(f\) :

Dimensionless stream function

\(C_{{\text{w}}}\) :

Surface concentration

\(\phi\) :

Dimensionless concentration

\(\tau_{{{\text{rx}}}}\) :

Wall shear stress

\(\mu_{0}\) :

Zero shear viscosity

\(q_{{\text{m}}}\) :

Wall mass flux

\(\tau\) :

Ratio of heat capacity

\({\text{Re}}_{x}\) :

Local Reynolds number

\({\text{Nu}}\) :

Local Nusselt Number

\(\upsilon\) :

Kinematic viscosity

\(k^{*}\) :

Mean absorption coefficient

\(\beta_{0}\) :

Magnetic field strength

\(\rho_{{{\text{cf}}}}\) :

Heat capacity of the base fluid

\(\tau_{{{\text{rx}}}}\) :

Wall shear stress

\(q_{{\text{m}}}\) :

Wall mass flux

References

  • Abbasi FM, Hayat T, Alsaedi A (2015) Peristaltic transport of magneto-nanoparticles submerged in water: model for drug delivery system. Physica E 68:123–132

    Article  CAS  Google Scholar 

  • Abbas SZ, Khan WA, Sun H, Ali M, Irfan M, Shahzed M, Sultan F (2020) Mathematical modeling and analysis of cross nanofluid flow subjected to entropy generation. Appl Nanosci. https://doi.org/10.1007/s13204-019-01039-9

    Article  Google Scholar 

  • Ahmad S, Hameed A, Khan K, Tauseef I, Ali M, Sultan F, Shahzad M (2019a) Evaluation of synergistic efect of nanoparticles with antibiotics against enteric pathogens. Appl Nanosci. https://doi.org/10.1007/s13204-019-01201-3

    Article  Google Scholar 

  • Ahmad S, Tauseef I, Haleem KS, Khan K, Shahzad M, Ali M, Sultan F (2019b) Synthesis of silver nanoparticle using leaves of catharanthus roseus and their antimicroblal activity. Appl Nanosci. https://doi.org/10.1007/s13204-019-01221-z

    Article  Google Scholar 

  • Alsaedi A, Awais M, Hayat T (2012) Effects of heat generation/absorption on stagnation point flow of nanofluid over a surface with convective boundary conditions. Commun Nonlinear Sci Numer Simulat 17:4210–4223

    Article  Google Scholar 

  • Ali M, Sultan F, Khan WA, Shahzad M, Arif H (2020a) Important features of expanding/contracting cylinder for cross magneto-nanofluid flow. Chaos Solitons Fractals 133:109656

    Article  Google Scholar 

  • Ali M, Sultan F, Khan WA, Shahzad M (2020b) Exploring the physical aspects of nanofuid with entropy generation. Appl Nanosci. https://doi.org/10.1007/s13204-019-01173-4

    Article  Google Scholar 

  • Choi SUS (1995) Enhancing thermal conductivity of fluids with nanoparticles, 231. ASME FED, New York

    Google Scholar 

  • Hayat T, Nawaz M (2011) Unsteady stagnation point flow of viscous fluid caused by an impulsively rotating disk. J Taiwan Inst Chem E 42(1):41–49

    Article  CAS  Google Scholar 

  • Haq I, Shahzad M, Khan WA, Irfan M, Mustafa S, Ali M, Sultan F (2019) Characteristics of chemical processes and heat source/sink with wedge geometry. Case Stud Thermal Eng 14:100432

    Article  Google Scholar 

  • Hussain Z, Rehman AU, Zeeshan R, Sultan F, Hamid TA, Ali M, Shahzad M, MHD instability of Hartmann fow of nanoparticles Fe2O3 in water. Appl Nanosci. https://doi.org/10.1007/s13204-020-01308-y

  • Khan WA, Haq I, Ali M, Shahzad M, Khan M, Irfan M (2018) Significance of static–moving wedge for unsteady Falkner-Skan forced convective flow of MHD cross fluid. J Braz Soc Mech Sci 40:470 https://doi.org/10.1007/s40430-018-1390-3

    Article  Google Scholar 

  • Khan MI, Hayat T, Waqas M, Alsaedi A (2017) Outcome for chemically reactive aspect in flow of tangent hyperbolic material. J Mol Liq 230:143–151

    Article  CAS  Google Scholar 

  • Khan WA, Sultan F, Ali M, Shahzad M, Khan M, Irfan M (2019a) Consequences of activation energy and binary chemical reaction for 3D fow of cross-nanofuid with radiative heat transfer. J Braz Soc Mech Sci 41:4. https://doi.org/10.1007/s40430-018-1482-0

    Article  CAS  Google Scholar 

  • Khan WA, Ali M, Sultan F, Shahzad M, Khan M, Irfan M (2019b) Numerical interpretation of autocatalysis chemical reaction for nonlinear radiative 3D flow of cross magnetofluid, Pramana. J Phys 92:16. https://doi.org/10.1007/s12043-018-1678-y

    Article  CAS  Google Scholar 

  • Khan WA, Ali M (2019) Recent developments in modeling and simulation of entropy generation for dissipative cross material with quartic autocatalysis. Appl Phys A 125:397

    Article  Google Scholar 

  • Khan WA, Sun H, Shahzad M et al (2020) Importance of heat generation in chemically reactive flow subjected to convectively heated surface. Indian J Phys. https://doi.org/10.1007/s12648-019-01678-2

    Article  Google Scholar 

  • Kumar KA, Sugunamma V, Sandeep N, Reddy JVR (2018) Impact of Brownian motion and thermophoresis on bioconvective flow of nanoliquids past a variable thickness surface with slip effects. Multidiscip Modeling Mater Struct. https://doi.org/10.1108/MMMS-02-2018-0023

    Article  Google Scholar 

  • Muhammad S, Ali G, Shah SIA, Irfan M, Khan WA, Ali M, Sultan F (2019) Numerical treatment of activation energy for the three-dimensional flow of a cross magnetonanoliquid with variable conductivity, Pramana. J Phys 93:40. https://doi.org/10.1007/s12043-019-1800-9

    Article  Google Scholar 

  • Reddy JVR, Sugunamma V, Sandeep N, Sulochana C (2016) Influence of chemical reaction, radiation and rotation on MHD nanofluid flow past a permeable flat plate in porous medium. J Nigerian Math Soc 35(1):48–65

    Article  Google Scholar 

  • Sheikholeslami M (2018) Numerical approach for MHD –Al2O3 water nanofluid transportation inside a permeable medium using innovative computer method. Comput Methods Appl Mech Engrg. https://doi.org/10.1016/j.cma.2018.09.042

    Article  Google Scholar 

  • Shahzad M, Sultan F, Haq I, Ali M, Khan WA (2019a) C-matrix and invariants in chemical kinetics: a athematical concept, Pramana. J Phys 92:64. https://doi.org/10.1007/s12043-019-1723-5

    Article  Google Scholar 

  • Shahzad M, Sultan F, Ali M, Khan WA, Irfan M (2019b) Slow invariant manifold assessments in multi-route reaction mechanism. J Mo Liq 284:265–270

    Article  CAS  Google Scholar 

  • Sulochana C, Ashwinkumar GP, Sandeep N (2018) Effect of frictional heating on mixed convection flow of chemically reacting radiative Casson nanofluid over an inclined porous plate. Alexandria Eng J 2573–2584.

  • Sultan F, Khan WA, Ali M, Shahzad M, Irfan M, Khan M (2019a) Theoretical aspects of thermphoresis and Brownian motion for three-dimensional flow of the cross fluid with activation energy, Pramana. J Phys 92:21. https://doi.org/10.1007/s12043-018-1676-0

    Article  Google Scholar 

  • Sultan F, Khan WA, Ali M, Shahzad M, Sun H, Irfan M (2019b) Importance of entropy generation and infnite shear rate viscosity for non-Newtonian nanofuid. Int J Mech Sci 41:439. https://doi.org/10.1007/s40430-019-1950-1

    Article  CAS  Google Scholar 

  • Sultan F, Shahzad M, Ali M, Khan WA (2019c) The reaction routes comparison with respect to slow invariant manifold and equilibrium points. AIP Adv 9:015212. https://doi.org/10.1063/1.5050265

    Article  CAS  Google Scholar 

  • Sultan F, Khan WA, Ali M, Shahzad M, Khan F, Waqas M (2019d) Slow invariant manifolds and its approximation in a multi-route reaction mechanism: a case study of iodized mechanism. J Mol Liq 288:111048

    Article  CAS  Google Scholar 

  • Sultan F, Mustafa S, Khan W et al (2020) A numerical treatment on rheology of mixed convective Carreau nanofluid with variable viscosity and thermal conductivity. Appl Nanosci. https://doi.org/10.1007/s13204-020-01294-1

    Article  Google Scholar 

  • Waqas M, Hayat T, Alsaedi A (2018) A theoretical analysis of SWCNT–MWCNT and nanofluids considering Darcy–Forchheimer relation. Appl Nanosci. Doi: https://doi.org/10.1007/s13204-018-0833-6.

    Article  Google Scholar 

  • Waqas M, Khan MI, Hayat T, Farooq S, Alsaedi A (2019) Interaction of thermal radiation in hydromagnetic viscoelastic nanomaterial subject to gyrotactic microorganisms. Appl Nanosci. https://doi.org/10.1007/s13204-018-00938-7

    Article  Google Scholar 

  • Wang J, Khan WA, Asghard Z, Waqas M, Ali M, Irfan M (2020) Entropy optimized stretching flow based on non-Newtonian radiative nanoliquid under binary chemical reaction. Comput Methods Programs Biomed 188:105274

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, Hazara University, Mansehra, 21300, Pakistan

    Mehboob Ali, Muhammad Shahzad & Faisal Sultan

  2. Department of Mathematics, Mohi-Ud-Din Islamic University, Nerian Sharif 12010, Islamabad, Azad Jammu and Kashmir, Pakistan

    Waqar Azeem Khan

Authors
  1. Mehboob Ali
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Muhammad Shahzad
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Faisal Sultan
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Waqar Azeem Khan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mehboob Ali.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ali, M., Shahzad, M., Sultan, F. et al. Numerical analysis of chemical reaction and non-linear radiation for magneto-cross nanofluid over a stretching cylinder. Appl Nanosci 10, 3259–3267 (2020). https://doi.org/10.1007/s13204-020-01385-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13204-020-01385-z

Keywords

Search

Navigation