Skip to main content

Advertisement

SpringerLink
Log in

Mixed convective flow of Maxwell nanofluid induced by vertically rotating cylinder

  • Original Article
  • Published:
Applied Nanoscience Aims and scope Submit manuscript

Abstract

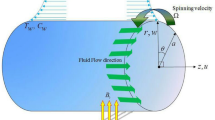
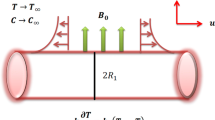
A study of mixed convection phenomenon in 3D flow of Maxwell nanofluid induced by vertically rotating and stretching cylinder is presented in current article. The Boussinesq approximation is used to predict the force of buoyancy due to which the free convection occurs in the fluid. Moreover, a popular Buongiorno model is utilized to reveal the influence of thermophoretic and Brownian forces for the transportation of energy in nanoliquid. The current physical problem of Maxwell nanofluid flow with energy transport is modeled under above consideration in form of partial differential equations (PDEs). Using the suitable flow similarities, the PDEs transformed into the set non-linear ordinary differential equations (ODEs) and then solved numerically by MATLAB built in scheme bvp4c. The outcomes of the problem are explored graphically and discussed with physical justification in rigorous way. In the flow and thermal analysis, it is noted that the higher values of both buoyancy and mixed convection parameters enhance the axial velocity and decline the swirl velocity, while these parameters decline the temperature and solutal fields, respectively. The higher value of thermophoretic force increases the thermal and solutal energy transport in the nanoliquid. Overall, it is revealed from the analysis that for large values of Reynolds number, the flow and energy transport decay exponentially faster to free stream conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Abbreviations

\(r,\phi ,z\) :

Cylindrical coordinates

u, v, w :

Velocity components

T :

Temperature of fluid

\(T_{w}\) :

Wall temperature

a :

Stretching rate

\(\nu\) :

Kinematic viscosity

\(\sigma\) :

Conductivity of fluid

\(T_{\infty }\) :

Ambient fluid temperature

\(B_{T}\) :

Thermal expansion coefficient

\(g_{1}\) :

Gravity strength

\(\alpha _{1}\) :

Thermal diffusivity

\(D_{B}\) :

Mass diffusivity

\(Q_{0}\) :

Heat source/sink

\(u_{\hbox {ss}}\) :

Surface stretching velocity

\(\eta\) :

Dimensionless variable

g :

Dimensionless azimuthal velocity

\(\theta\) :

Dimensionless temperature

\(\hbox {Re}\) :

Reynolds number

\(N_{t}\) :

Thermophoretic parameter

\(N_{1}\) :

Mixed convection parameter

\(\hbox {Gr}\) :

Grashof numbers for temperature

\(\hbox {Nu}\) :

Nusselt number

\(\Pr\) :

Prandtl number

\(\lambda _{1}\) :

Fluid relaxation time

\(\mathbf {B}\) :

Magnetic field

C :

Concentration in fluid

\(C_{w}\) :

Wall concentration

E :

Rotational velocity

\(\mu\) :

Dynamic viscosity

\(\rho\) :

Density of fluid

\(C_{\infty }\) :

Ambient concentration

\(B_{C}\) :

Solutal expansion coefficient

\(B_{0}\) :

Strength of magnetic field

\(\tau\) :

Heat capacity ratio

\(D_{T}\) :

Thermophoresis coefficient

\(c_{p}\) :

Specific heat capacity

\(v_{\hbox {sr}}\) :

Surface rotation velocity

\(f^{\prime }\) :

Dimensionless axial velocity

\(\frac{f}{\sqrt{\eta }}\) :

Dimensionless radial velocity

\(\beta _{1}\) :

Maxwell parameter

M :

Magnetic number

\(N_{b}\) :

Brownian diffusion parameter

\(\lambda\) :

Buoyancy parameter

\(\hbox {Gr}^{*}\) :

Grashof numbers for concentration

\(\hbox {Sh}\) :

Sherwood number

\(\hbox {Le}\) :

Lewis number

References

  • Ahmed SE, Raizah ZAS, Aly AM (2017) Entropy generation due to mixed convection over vertical permeable cylinders using nanofluids. J King Saud Univ Sci. https://doi.org/10.1016/j.jksus.2017.07.010

    Article  Google Scholar 

  • Ahmed J, Khan M, Ahmad L (2019) Stagnation point flow of Maxwell nanofluid over a permeable rotating disk with heat source/sink. J Mol Liq 287:110853

    Article  CAS  Google Scholar 

  • Ahmed J, Khan M, Ahmad L (2019) MHD swirling flow and heat transfer in Maxwell fluid driven by two coaxially rotating disks with variable thermal conductivity. Chin J Phys 60:22–34

    Article  Google Scholar 

  • Bai Y, Huo L, Zhang Y, Jiang Y (2019) Flow, heat and mass transfer of three-dimensional fractional Maxwell fluid over a bidirectional stretching plate with fractional Fourier’s law and fractional Fick’s law. Comp Math Appl 78(8):2831–2846

    Article  Google Scholar 

  • Cheng WT, Lin CH (2007) Melting effect on mixed convective heat transfer with aiding and opposing external flows from the vertical plate in a liquid-saturated porous medium. Int J Heat Mass Transf 50:3026–3034

    Article  Google Scholar 

  • Ellahi R, Sait S, Shehzad N, Ayaz Z (2019) A hybrid investigation on numerical and analytical solutions of electro-magnetohydrodynamics flow of nanofluid through porous media with entropy generation. Int J Numer Meth Heat Fluid Flow 30(2):834–854

    Article  Google Scholar 

  • Ellahi R, Hussain F, Abbas SA, Sarafraz MM, Goodarzi M, Shadloo MS (2020) Study of two-phase Newtonian nanofluid flow hybrid with Hafnium particles under the effects of slip. Inventions 5:6. https://doi.org/10.3390/inventions5010006

    Article  Google Scholar 

  • Fang TG (2007) Flow over a stretchable disk. Phys Fluids 19(12):128105. https://doi.org/10.1063/1.2823572

    Article  CAS  Google Scholar 

  • Fang T, Yao S (2011) Viscous swirling flow over a stretching cylinder. Chin Phys Lett 28:114702

    Article  Google Scholar 

  • Guha A, Sengupta S (2017) Non-linear interaction of buoyancy with von Kármán’s swirling flow in mixed convection above a heated rotating disc. Int J Heat Mass Transf 108:402–416

    Article  CAS  Google Scholar 

  • Hashim AHamid, Khan M (2018) Unsteady mixed convective flow of Williamson nanofluid with heat transfer in the presence of variable thermal conductivity and magnetic field. J Mol Liq 260:436–446

    Article  CAS  Google Scholar 

  • Hayat T, Ullah I, Alsaedi A, Waqas M, Ahmad B (2017) Three-dimensional mixed convection flow of Sisko nanoliquid. Int J Mech Sci 133:273–282

    Article  Google Scholar 

  • Hsiao KL (2016) Stagnation electrical MHD nanofluid mixed convection with slip boundary on a stretching sheet. Appl Therm Eng 98:850–861

    Article  CAS  Google Scholar 

  • Hsiao KL (2017a) To promote radiation electrical MHD activation energy thermal extrusion manufacturing system efficiency by using Carreau-Nanofluid with parameters control method. Energy 130:486–499

    Article  Google Scholar 

  • Hsiao KL (2017b) Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int Heat Mass Transf 112:983–990

    Article  Google Scholar 

  • Hsiao KL (2017c) Combined electrical MHD heat transfer thermal extrusion system using Maxwell fluid with radiative and viscous dissipation effects. Appl Therm Eng 112:1281–1288

    Article  CAS  Google Scholar 

  • Kármán V (1921) Über laminare und turbulente Reibung. Z Angew Math Mech 1:233–252

    Article  Google Scholar 

  • Khan SU, Ali Shehzad S, Rauf A, Ali N (2018) Mixed convection flow of couple stress nanofluid over oscillatory stretching sheet with heat absorption/generation effects. Results Phys 8:1223–1231

    Article  Google Scholar 

  • Li W, Feng ZZ (2013) Laminar mixed convection of large-Prandtl-number in-tube nanofluid flow, Part II: correlations. Int J Heat Mass Transf 65:928–935

    Article  CAS  Google Scholar 

  • Malik R, Khan M (2018) Numerical study of homogeneous-heterogeneous reactions in Sisko fluid flow past a stretching cylinder. Results Phys 8:64–70

    Article  Google Scholar 

  • Mustafa M (2017) An analytical treatment for MHD mixed convection boundary layer flow of Oldroyd-B fluid utilizing non-Fourier heat flux model. Int J Heat Mass Transf 113:1012–1020

    Article  CAS  Google Scholar 

  • Nazari S, Ellahi R, Sarafraz MM, Safaei MR, Asgari A, Akbari OA (2019) Numerical study on mixed convection of a non-Newtonian nanofluid with porous media in a two lid-driven square cavity. J Therm Anal Calorim. https://doi.org/10.1007/s10973-019-08841-1

    Article  Google Scholar 

  • Raees A, Wang RZ, Xu H (2018) A homogeneous-heterogeneous model for mixed convection in gravity-driven film flow of nanofluids. Int Commun Heat Mass Transf 95:19–24

    Article  CAS  Google Scholar 

  • Riaz A, Bhatti MM, Ellahi R, Zeeshan A, Sait SM (2020) Mathematical analysis on an asymmetrical wavy motion of blood under the influence entropy generation with convective boundary conditions. Symmetry 12:102. https://doi.org/10.3390/sym12010102

    Article  Google Scholar 

  • Sharma PR, Sinha S, Yadav RS, Filippov AN (2018) MHD mixed convective stagnation point flow along a vertical stretching sheet with heat source/sink. Int J Heat Mass Transf 117:780–786

    Article  Google Scholar 

  • Sprague MA, Weidman PD (2011) Three-dimensional flow induced by torsional motion of a cylinder. Fluid Dyn Res 43:015501

    Article  Google Scholar 

  • Turkyilmazoglu M (2017) Mixed convection flow of magnetohydrodynamic micropolar fluid due to a porous heated/cooled deformable plate: exact solutions. Int J Heat Mass Transf 106:127–134

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Quaid-i-Azam University, Islamabad, 44000, Pakistan

    Awias Ahmed, Masood Khan & Jawad Ahmed

  2. Department of Basic Sciences, University of Engineering and Technology, Taxila, 47050, Pakistan

    Jawad Ahmed

Authors
  1. Awias Ahmed
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Masood Khan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jawad Ahmed
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Awias Ahmed.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ahmed, A., Khan, M. & Ahmed, J. Mixed convective flow of Maxwell nanofluid induced by vertically rotating cylinder. Appl Nanosci 10, 5179–5190 (2020). https://doi.org/10.1007/s13204-020-01320-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13204-020-01320-2

Keywords

Search

Navigation