Abstract
This study is aimed to predict potential soil erosion in the Langat River Basin, Malaysia by integrating Remote Sensing (RS) and Geographical Information System (GIS) with the Revised Universal Soil Loss Equation (RUSLE) model. In RUSLE model, parameters such as rainfall erosivity factor (R), soil erodibility factor (K), slope length and steepness factor (LS), vegetation cover and management factor (C) and support practice factor (P) are determined based on the input data followed by the spatial analysis process in the GIS platform. Rainfall data from 2008-2015 are collected from the 29 rain gauge stations located within the study area. From the analysis, the magnitude of RUSLE model obtained corresponding to the parameter R, K, LS, C and P factors is varied between 800 to 3000 MJ mm ha− 1 h− 1 yr− 1, 0.035–0.5 Mg h MJ− 1 mm− 1, 0–73.00, 0.075–0.77 and 0.2–1.00, respectively. Findings of this study indicates that based on the calculated RUSLE parameter values, about 95% of the Langat River Basin area have been classified as a very low to a low erosion vulnerability. Findings of this study would greatly benefits a decision maker in proposing a suitable soil management and conservation practices for the river basin.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
The soil erosion process is involved in three major parts of a complex dynamic way which are detachment, transportation and accumulation of eroded particles either in site or offsite on the earth surface (Jain et al. 2001). This process is propagated slowly over large period having affected the geomorphology of rural area, and the soil fertility get increased in flood plains. However, several human activates most likely the deforestation, overgrazing, inaccurate tillage method and unscientific agriculture practice often lead to the worst erosion hazards (Lal 2003, Weifeng and Bingfang 2008). Although the naturally occurred erosion is ranged between 0.1 and 1 t ha −1 yr−1, this figure is increased by 10–1000 times getting intermingled with the aforesaid human activities (De Franchis and Ibanez 2003). The consequence resulted from soil erosion in the watersheds is the gradual decrease in fertility due to the successive removal of their topsoils. Having deposited the removal soils onto the beds of rivers, lakes and reservoir, they suffer from numerous problems; the occurrence of flash flood and hindrance of the normal water flow are the most common (Weifeng and Bingfang 2008; Zhou et al. 2008). In addition, the surface water quality become worsen, and the consequences associated are eutrophication, turbidity and pollution, thus deteriorating the landscape beauty and the aquatic biodiversity (Onyando et al. 2005; Sthiannopkao et al. 2007; Zhou et al. 2008; Bewket and Teferi 2009; Wang et al. 2009).
To get rid of our environment as well as economy and ecology from getting affected by the adverse situations, adapting the best soil management practice is the only option (Zhang et al. 2009; Arefin et al. 2020). Before proposing any soil management practice to have its optimum efficiency in soil conservation, several parameters such as the potential amount, risk category and spatial distribution of soil erosions are needed to know obviously. As an empirical model, the widely used Revised Universal Soil Loss Equation (RUSLE) is the best alternative to predict the soil erosion that offers better visualization of the spatial distribution of soil erosion integrated with Geographic Information System (GIS) and Remote Sensing (RS), besides less time, and data needed to simulate (Fu et al. 2005; Yue-Qing et al. 2008; Das et al. 2020).
To predict the soil erosion, this model requires several basic factors related to rainfall, soil type, slope and land use (Weifeng and Bingfang 2008; Kouli et al. 2009). These factors will be interpreted in the model as separate raster layers, and the analysis will then be based on each grid’s value (Bhattarai and Dutta 2007). Some studies, either plot scale or watershed scale, have employed the RUSLE model integrated with the GIS to analyze soil erosion (Yue-Qing et al. 2008; Kouli et al. 2009; Terranova et al. 2009; Islam et al. 2018). Although there are few studies have been done using RUSLE models to predict soil loss in few watersheds in Malaysia (Almas and Jamal 1999; Teh 2011; Kamaludin et al. 2013; Jaafar et al. 2020), an integrated approach of RUSLE and GIS using remotely sensed satellite data and observation data is the first time to be implemented in this study by focusing on the Langat River Basin.
Study area
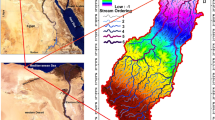
The Langat River Basin is located within the latitudes 2° 40′ 12″ N to 3° 16′ 15″ N and the longitudes 101° 19′ 20″ E to 102° 1′ 10″ E at the southern region of Selangor State, west Malaysia. The drainage area of the basin is 2140.6 km2, and the overall shape and morphology along with the rain gauge location (plain map) of the basin were viewed as digital elevation model (DEM) (Fig. 1). It is situated about 40 km from Kuala Lumpur and the length of the main river course is 141 km and the main tributaries of the Langat River are the Semenyih River, Lui River and Beranang River. The data used in this study to predict the annual soil loss and their sources are illustrated in Table 1.
Geology and soils
The bedrock in the mountain area which is a bone of peninsula is formed from granite, and it is extended to hilly areas near kg Cheras. The layer of the hilly areas is comprised of metamorphosed sandstone, shale, mudstone and schist, and it is called Kenny Hill Formation and Kajang Formation. The granite and also upper part of the bedrock are weathered, and several parts are heavily weathered to the depth of several meters (JICA 2002). The thick quaternary layers are deposited on the bedrock in the low flatlands. From the top to the bottom, the deep of the quaternary layer is about 0.5–5.5 m, Beruas Formation with peat layers at the top, clayey Gula Formation and Kempadang Formation starting from the hilly areas having 40–50 m depth near the seacoast. The Simpang Formation of sand is lying underneath, and the gravel thickness is about 50 m and higher than 100 m in the flatlands (JICA 2002). However, a geology map and the soil details of the study area are presented in Fig. 2 and Table 2 based on the present version (3.6) of the digitized Soil Map of the World which is prepared by Food and Agriculture Organization of the United Nations.
Meteorological and vegetation conditions
The daily temperature fluctuates between 24 °C and 25 °C, and it remains uniform throughout the year over the study area. The humidity of the study area is high during the year, and it exceeds by 90%. The mean daily sunshine is obtained 6 h, and daily evaporation is 3.48 mm, while the mean surface wind speed is 1.59 m s−1(climate data of UKM Bangi Station from 1985 to 2000).The luxurious growth of vegetation in the study area is palpable due to porous laterite soil and heavy rainfall. The eastern and northeast regions are covered with dense forests and are located at the upper portion of the basin. The different types of the forest varied from evergreen scrub to fully grown forest which can be seen in the basin.
Materials and methodology
The widely used RUSLE model, employed in this study, is capable of predicting and visualizing the temporal and spatial variations of soil erosion once integrated with GIS. RUSLE model considers that the detachment and transportation of soil particles are function of sediment load of the flow. The erosion is not dependent on the sources of eroded materials but it depends on the the carrying capacity of flow. A detachment of sediment loads no longer occurs when it reaches the carrying capacity of the flow. The sedimentation also happens during the preceding portion of hydrograph while the flow rate decreases (Kim 2006). However, The basic parameters needed in RUSLE model to calculate the soil loss are the rainfall events, digital elevation model (DEM), soil type and land use data; the overall methodology is shown schematically in Fig. 3.
RUSLE parameter estimation
In this study, the annual average soil was predicted using RUSLE model where the model parameters were generated through DEM and satellite images. All the input parameters were integrated as raster layers in GIS platform. Here, each layer stands for an individual RUSLE parameter that is comprised of numerous grids or square cells. According to Eq. (1), the average annual soil loss was predicted using the raster calculator in ArcGIS software.
where A is the soil loss (t ha−1 yr−1); R is the rainfall erosivity factor (MJ mm ha−1 h−1 yr−1); K is the soil erodibility factor (t h MJ−1 mm−1); LS is the slope length and steepness factor (dimensionless); C is the vegetation cover and management factor (dimensionless); and P is the support practice factor (dimensionless).
Rainfall erosivity factor (R) The rainfall erosivity factor (R) is the quantity which indicates the cumulative soil detachment capability of the rainstorms over the year. Continuous precipitation data are needed to calculate the R factor, and it reflects the effect of rainfall intensity in the water erosion process (Wischmeier and Smith 1978). Two most important characteristics of a storm that determine its erosivity are the amount of rainfall and the peak intensity sustained over an extended period. The rainfall erosivity factor can be determined easily if the rainfall intensity data are found in a suitable form. Here, the R factor has been calculated based on annual rainfall data of 29 rain gauge stations in and around the study area for 8 years, 2008–2015. Based on best estimation practice, a typical calculation of the R factor for a particular rain gauge station is presented in Table 3, where R is the rainfall erosivity factor in MJ mm ha−1 h−1 yr−1 and Rm and Rr are also the rainfall erosivities according to Morgan (2005) and Roose (1977); P is the annual rainfall (mm). Having been calculated the R factors for individual rain gauge stations, the Kriging, an interpolation method, is then employed to figure out the spatial distribution of the R factor over the study area; the erosivity map is presented in Fig. 4.
Soil erodibility factor (K) The soil erodibility factor (K) states the inherent erodibility of the soils, and that measures its vulnerability to detachment and transportation by falling raindrops and overland flow. K factor can be determined experimentally integrating several soil parameters. Soil erosion rate obtained by unit rainfall erosivity indicates the value of K factor. In general, the direct measurement at natural runoff plots can offer the best soil erodibility (K) determination practice. In fact, the K value of clay soils is low because they exhibit a considerable resilient against their particle detachment. In addition, sandy soil also has a low K value because of its high infiltration rates and decreased runoff and the eroded particles are hard to transport. K values are moderate to high for silt loam because of its easy detachability and low to moderate infiltration capacity, thereby producing moderate to high runoff and sediment transportation as well. The highest K value is silt soils as the soils already crust and the runoff rates are high. However, in this study, the soil map of Langat Basin provided by Ministry of Natural Resources and Environment Malaysia (2010) has been used to present the spatial variation of soil properties. According to this map, there were 14 different soil series and their corresponding K values. Finally, the soil erodibility map was generated assigning the soil series with the corresponding K factors (Fig. 5).
Slope length and steepness factor (LS) The slope length and steepness factor (LS) comprise two factors: (1) slope length and (2) slope steepness. The LS factor signifies a ratio of soil loss under given condition at a site with the standard slope steepness of 9% and slope length of 22.1 m. The effect of slope length on erosion is called slope length factor (L); the slope length is the distance between two points: Initial one is the overland flow commencing point and the final one is the termination point. Therefore, when the slope length is increased the soil loss per unit area is increased simultaneously. The effect of slope steepness on erosion is denoted as slope steepness factor (S).The impact of slope steepness on soil erosion is higher than that of the slope length. The steeper the slope, the greater the erosion; the slope steepness between 10 and 25% leads to the severest erosion. The LS factor is then calculated using Eq. (2):
where X = slope length (m); S = slope gradient (%), the values of X and S were also derived through the DEM of the study area. To calculate the X as per Eq. (2), flow accumulation was derived having conducted the FILL and flow direction operation to the DEM in ArcGIS10.1.
Substituting the X to Eq. (2), LS equation is appeared as follows:
The magnitude of “m” is varied from 0.2 to 0.5 depending upon the slope types as shown in Table 4.
Vegetation cover and management factor (C) In RUSLE, the land cover of the study area is represented by the vegetation cover and management factor that sets a significant effect on erosion. Reducing the erosion up to said extent, the C is the only factor that can easily be manipulated. More specifically, the C factor stands for vegetation cover percentage and results in the ratio of soil loss from specific crops to the equivalent loss from tilled, bare test plots. The magnitude of C factors undergoes changes with time due to the variability in vegetation types and their growth and densities. Considering the normalized difference vegetation index (NDVI) as a function of vegetation growth, the satellite image, e.g., Landsat 8 imagery, offers a convenient computation method for C factor.
In Eq. (5), NIR represents the reflection of the near-infrared portion of the electromagnetic spectrum and IR signifies the reflection in the visible spectrum. The NDVI value is ranged between − 1.0 and + 1.0 where the relatively higher and the lower values stand for, respectively, green area and other common surface materials. More specifically, the bare soil is represented by the value closer to 0, whereas the water bodies are defined with the negative values. In this study, the NDVI calculation was based on the Landsat 8 imagery with spatial resolution of 30 m. Spatial distribution of C factor over the study area was calculated according to Eq. 6 that was developed by Lin et al. (2002). Anache et al. (2014) found it as the most suitable equation for calculating C factor, especially in Asian countries.
Support practice factor (P) The conservation and support practice factor (P) are quantified as the ratio of soil loss occurred at a plot under conservation and support practiced to that of straight-row farming up and down the slope. Such practices reduce the erosion potential of the runoff which is influenced by drainage patterns, the runoff concentration, the runoff velocity and hydraulics forces resulted from runoff. Similar to the C factor, the magnitude of the P factor also varied from 0 to 1.0 where a good conservation and support practice is represented by the value imminent to 0 and the poor conservation practice is what imminent to 1.0. Here, the P factor map of the study area was generated using the pre-defined P factor values corresponding to the land use classes (Table 5).
Results and discussion
Rainfall erosivity factor (R)
The R factor was determined in this study using the rainfall data provided by the Malaysian Meteorological Department (MMD), of which 29 rain gauge stations were used where the average annual rainfall varied from 100 to 3222 mm in the duration of 2008–2015. However, the average annual rainfall over the catchment area is 2322 mm. It was found that the R factor in Langat Basin varies from 820 to 3000 MJ mm ha−1h−1 yr−1 and its spatial distribution is presented in Fig. 3. Other than the central area of the catchment where R value predicted the maximum, the rest area is found with uniform distribution of R values.
Soil erodibility factor (K)
The resentence of soils and/or soil profile against erosion is represented by the soil erodibility factor (K) (Renard et al. 1997). There are 15 different soil types found in the study area with different K factor values. The K values range between 0.035 and 0.50 Mg h MJ−1mm−1. It should be noted that maximum major portion of the study area has been characterized with the lower value of K, i.e., 0.035 to 0.128 Mg h MJ−1mm−1. Only the soil series steep land appeared with relatively higher value of K, but it covers very small area (1.12%) compared to the entire basin. This series is mostly characterized by fine sand and silt fraction which increase the susceptibility to erosion and thereby K value as well. Available soil series and their corresponding K values are presented in Table 6.
Slope length and steepness factor (LS)
In RUSLE model, the impact of slope length and slope steepness on soil erosion process is signified by the topographic factor (LS). The flow accumulation and slope percentage are inputs to calculate LS factor. The result of the analysis shows that the LS value increases in the range of 0 to 72 (Fig. 6). The very low LS values (0 to 0.86) were found almost over the basin, and hence, from topographical conditions, it might be considered that the study area is no more vulnerable to erosion hazard.
Vegetation cover and management factor (C)
In RUSLE model, the effects of available vegetation cover for any ground surface either agricultural practices or not in reducing the soil erosion are numerically represented by the C factor. Here, the C factor retrieval has been done using the Landsat 8 imagery along with NDVI. The NDVI values found in the study area are ranged from − 0.30 to + 0.60. The negative value is obtained for the water body, while the maximum value for dense forest. However, the C factor values calculated here are ranged from 0.075 for forest to 0.75 for non-vegetative area; all the themes are presented in Fig. 7.
Support practice factor (P)
Based on the land use map of the study area, it is observed that the basin is highly dominated by agricultural land, especially by the palm tree and some other permanent crops (Fig. 8). In fact, about 39.25% study area is covered with the cropping practice; thus, the corresponding P factor of the area was considered 0.2. Besides, little area is found with horticulture land as well as short-term crops whose P value was 0.4. In Langat River Basin, at least 25% area was occupied by forest including the swamp mangrove and the wetland forest. The urban, settlements and associated non-agricultural areas are found together approximately at 20% area with a P value of 1.00. Small patches of idle grassland are found at the southern part of the basin with a P factor value of 0.20. However, the P value for water body and some others has been considered as 0.50 and 0.70, respectively.
Potential annual soil erosion estimation
Integrating the RUSLE parameter in GIS interface, the potential annual soil loss (A) in Langat was analyzed on pixel basis and its spatial distribution was presented over the study area. The average annual soil loss estimated for the study area is varied between 0 and 847.95 t ha−1 yr−1. This estimation result of the accumulated soil loss of the basin is 42,132.65 t yr−1taking into account the land use map of the year 2010. Based on erosion susceptibility, the entire basin was classified into seven categories, i.e., very low, low, moderate, high, severe, extreme and exceptional erosion area. In this study, a large area in the river basin is found under a low soil erosion category. The extreme to exceptional soil erosion occurred only in a few regions with barren lands and the steep slope; moderate soil erosion occurs at the foothills as there were agricultural areas next to the mild slope.
Conclusions
The RUSLE integrates all the erosion parameters in RS and GIS framework to demarcate precisely the erosion-vulnerable zones. In this study, the spatial distribution of different erosion susceptible areas in Langat River Basin was figured out along with the estimated erosion figure of 42,132.65 t yr−1. According to erosion map of the river basin, only 5% of the area are classified under the high and extreme erosion category, whereby the erosion control measures surely be practiced to control its erosion severity. The outcome of this research is crucial to all agencies or individuals who are directly or indirectly associated with the basin. In developing management scenarios, it will help the policymakers or basin managers in providing the options for managing the soil erosion hazards in a well-manageable and efficient way (Fig. 9).
References
Almas M, Jamal T (1999) Soil loss prediction (using Rusle) and comparison with measured soil loss. Pak J Biol Sci (Pak) 2:1536–1539
Anache JA, Bacchi CG, Alves-Sobrinho T (2014) Modeling of (R) USLE C-factor for pasture as a function of normalized difference vegetation index. Eur Int J Sci Technol 3(9):214–221
Arefin R, Mohir MMI, Alam J (2020) Watershed prioritization for soil and water conservation aspect using GIS and remote sensing: PCA-based approach at northern elevated tract Bangladesh. Appl Water Sci 10(4):1–19
Bewket W, Teferi E (2009) Assessment of soil erosion hazard and prioritization for treatment at the watershed level: case study in the Chemoga watershed, Blue Nile Basin, Ethiopia. Land Degrad Dev 20(6):609–622
Bhattarai R, Dutta D (2007) Estimation of soil erosion and sediment yield using GIS at catchment scale. Water Resour Manag 21(10):1635–1647
Das B, Bordoloi R, Thungon LT, Paul A, Pandey PK, Mishra M, Tripathi OP (2020) An integrated approach of GIS, RUSLE and AHP to model soil erosion in West Kameng watershed, Arunachal Pradesh. J Earth Syst Sci 129(1):1–18
De Franchis L, Ibanez F (2003) Threats to soils in Mediterranean Countries. Plan Bleu-Centre d’activités régionales, Sophia Antipolis
Fu B, Zhao W, Chen L, Zhang Q, Lu Y, Gulinck H, Poesen J (2005) Assessment of soil erosion at large watershed scale using RUSLE and GIS: a case study in the Loess Plateau of China. Land Degrad Dev 16(1):73–85
Islam MR, Jaafar WZW, Hin LS, Osman N, Din MAM, Zuki FM, Srivastava P, Islam T, Adham MI (2018) Soil erosion assessment on hillslope of GCE using RUSLE model. J Earth Syst Sci 127(4):50
Jaafar WZW, Islam MR, Hin LS, Osman N, Othman FB, Din MAM, Karim R (2020) Assessment of rainfall-induced soil erosion on hillslope: a case study at the Guthrie Corridor Expressway, Malaysia. Sustainable Water Resources Manag 6(2):1–10
Jain SK, Kumar S, Varghese J (2001) Estimation of soil erosion for a Himalayan watershed using GIS technique. Water Resour Manag 15(1):41–54
JICA M (2002) The study on the sustainable groundwater resources and environmental management for the Langat Basin in Malaysia. Kuala Lumpur
Kamaludin H, Lihan T, Ali Rahman Z, Mustapha M, Idris W, Rahim S (2013) Integration of remote sensing, RUSLE and GIS to model potential soil loss and sediment yield (SY). Hydrol Earth Syst Sci Dis 10(4):4567–4596
Kim HS (2006) Soil erosion modeling using RUSLE and GIS on the IMHA Watershed. Colorado State University, South Korea
Kouli M, Soupios P, Vallianatos F (2009) Soil erosion prediction using the revised universal soil loss equation (RUSLE) in a GIS framework, Chania, Northwestern Crete, Greece. Environ Geol 57(3):483–497
Lal R (2003) Soil erosion and the global carbon budget. Environ Int 29(4):437–450
Lin C-Y, Lin W-T, Chou W-C (2002) Soil erosion prediction and sediment yield estimation: the Taiwan experience. Soil Tillage Res 68(2):143–152
Morgan RPC (2005) Soil erosion and conservation. Blackwell, UK
Onyando J, Kisoyan P, Chemelil M (2005) Estimation of potential soil erosion for river perkerra catchment in Kenya. Water Resour Manag 19(2):133–143
Renard KG, Foster GR, Weesies G, McCool D, Yoder D (1997) Predicting soil erosion by water: a guide to conservation planning with the Revised Universal Soil Loss Equation (RUSLE). US Department of Agriculture, Agricultural Research Service Washington, Washington
Roose E (1977) Application of the universal soil loss equation of Wischmeier and Smith in West Africa. In: Paper presented at the soil conservation and management in the humid tropics, Proceedings of the international conference
Sthiannopkao S, Takizawa S, Homewong J, Wirojanagud W (2007) Soil erosion and its impacts on water treatment in the northeastern provinces of Thailand. Environ Int 33(5):706–711
Teh SH (2011) Soil erosion modeling using RUSLE and GIS on Cameron highlands, Malaysia for hydropower development. Master’s thesis, The School for Renewable Energy Science, University of Iceland
Terranova O, Antronico L, Coscarelli R, Iaquinta P (2009) Soil erosion risk scenarios in the Mediterranean environment using RUSLE and GIS: an application model for Calabria (southern Italy). Geomorphology 112(3):228–245
Wang G, Hapuarachchi P, Ishidaira H, Kiem AS, Takeuchi K (2009) Estimation of soil erosion and sediment yield during individual rainstorms at catchment scale. Water Resour Manag 23(8):1447–1465
Weifeng Z, Bingfang W (2008) Assessment of soil erosion and sediment delivery ratio using remote sensing and GIS: a case study of upstream Chaobaihe River catchment, north China. Int J Sedim Res 23(2):167–173
Wischmeier WH, Smith DD (1978) Predicting rainfall erosion losses-A guide to conservation planning. Predicting rainfall erosion losses-A guide to conservation planning. US Department of Agriculture, Washington, DC
Yue-Qing X, Xiao-Mei S, Xiang-Bin K, Jian P, Yun-Long C (2008) Adapting the RUSLE and GIS to model soil erosion risk in a mountains karst watershed, Guizhou Province, China. Environ Monit Assess 141(1–3):275–286
Zhang Y, Degroote J, Wolter C, Sugumaran R (2009) Integration of modified universal soil loss equation (MUSLE) into a GIS framework to assess soil erosion risk. Land Degrad Develop 20(1):84–91
Zhou P, Luukkanen O, Tokola T, Nieminen J (2008) Effect of vegetation cover on soil erosion in a mountainous watershed. CATENA 75(3):319–325
Acknowledgements
The authors would like to acknowledge the University of Malaya for overall financial supports. This research was carried out by the University of Malaya Research Grant (UMRG) under the project “Investigate Soil Hydrological Aspects and Vegetation Cover for Slope Erosion” Project no. PR005B-13SUS.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Islam, M.R., Jaafar, W.Z.W., Hin, L.S. et al. Development of an erosion model for Langat River Basin, Malaysia, adapting GIS and RS in RUSLE. Appl Water Sci 10, 165 (2020). https://doi.org/10.1007/s13201-020-01185-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13201-020-01185-4