Multi-objective linear fractional inventory problem under intuitionistic fuzzy environment

Abstract

In this paper, we have assumed an inventory multi-objective optimization model under intuitionistic fuzziness. In modelling, we have considered the situations where triangular intuitionistic fuzzy numbers used to express some of the input information which associated with decision variables. Further, a ranking function approach by considering linear and the nonlinear degree of membership functions have been used to obtain the crisp form of the fuzzy parameters. Finally, the fuzzy goal programming approach has been used to solve the resultant model to obtain the optimal ordering quantity. Also, a comparative study of the formulated problem under intuitionistic fuzziness has been done with a deterministic model of inventory. The concept of the paper is explained through a numerical example.

1 Introduction

In industries, the top management personnel’s, who are also the decision maker (DM), are not able to accurately estimate the business-oriented input information’s. Since due to complex situations in business nobody can judge the actual parameters. These parameters are also known as the independent factors. However, the DM has some rough idea about these independent factors. The DM can roughly express these types of uncertainties by using fuzzy numbers either with non-negative trapezoidal or triangular IFN. Zadeh (1965) gave the concept of well known fuzzy set theory to tackle the uncertainty. Later on, with some advancement the concept of intuitionistic fuzzy set (IFS) theory was specified by Atanassov (1986, 1989), to tackle the intricate ambiguity in decision-making problems. Some important applicationsof IFS theory have been discussed by the following authors: Nagoorgani and Ponnalagu (2012), Mahapatra and Roy (2013), Garg and Rani (2013), Garg et al. (2013, 2014a, b), Wu and liu (2013), Chakraborty et al. (2014), De and Sana (2014), Garg (2014, 2015a, b, 2016a, b, 2017, 2018), Singh and Garg (2017), Garg and Arora (2017), and many others.

Today multi-objective optimization model has been recurrently formulated by the practitioners or researchers in almost every field of the research study. The best part of the multi-criterion decision making is to optimize all objective functions simultaneously in a single frame. The decision maker can also set up an aspiration level to each of the objective function which is considered as their goal values. In particular, most of the models formulated for supply chains management includes transportation problem, production planning problem and inventory problem based on a deterministic view of the decision maker. In the same manner, a multi-criteria decision-making model with fuzzy parameters is found to be more realistic than the deterministic model. However, while modelling the optimization model, we have found that data are not often precisely known to the decision maker due to incomplete and inadequate information. Therefore in such situation first role of the DM is to study the pattern of data after then make it convenient for modelling. This paper deals with IFS concepts in inventory management. Inventory management is the lifeblood of every supply chain, and if it accurately managed then it plays an essential role in reducing the total cost, brings productivity for companies; otherwise, it serves as legal responsibility for the concerned authority. Moreover, as the prerequisite of the business changes, the inventory management needs to be modified as accordingly. Inventory management is concerned with the flow of materials from vendors (suppliers) to production and the subsequent movement of products through distribution centres to the customers at the right time to maintain the demand and supply ratio with the minimum cost of the product. The primary objective of inventory management is specifying the quantity of items when it should be ordered from the vendors (suppliers) and how much it is? Interested readers can read the research of Tersine (1994), Pentico and Drake (2011), for getting a proper overview on the inventory models.

From the last decade or with the commencement of the twentieth era, optimization technique has been recurrently used by the researchers in the field of inventory management. The researchers have developed many models related to the inventory control, but the conventional economic order quantity (EOQ) model proposed by Harris (1913) is still considered the most popular inventory model. Due to its ease of use and simplicity, many researchers tried to extend it under different realistic assumptions. Hariri and Abou-El-Ata (1997) formulated inventory model as a geometric programming problem with the assumption of varying deterministic ordering cost for a multi-item lot size problem. Sabri and Beamon (2000) formulated the most significant part of a supply chain management as a mathematical programming problem and minimize the cost related to production cost and delivery time of strategic and operational planning respectively. Fung et al. (2003) formulated multi production planning problem with ambiguous demands and capacities with the purpose to obtain the optimal order quantities. The fractional programming problem formulation of inventory management first proposed by Sadjadi et al. (2005). They considered a deterministic model with the primary aim was to optimise the holding cost and entirely ordered quantities simultaneously. Similarly, Chen (2005) used LFPP approach under the stochastic environment in inventory problem. Later on, two different types of inventory model proposed by Khanra et al. (2010), Valliathal and Uthayakumar (2010) with reliant demand rate. Yadav et al. (2010) established a model with small storage volume with deterioration rate under some reliability and flexibility assumptions. Banerjee and Roy (2010) formulated stochastic inventory model by considering fuzzy cost function and uniform, exponential, and normal lead time demand. The developed model is solved by fuzzy intuitionistic optimization technique and Zimmermann (1978) fuzzy optimization technique respectively. Kundu and Chakrabarti (2011) discussed the circumstances of ambiguous demand and deterioration rate under the tolerable delay in disbursements for a lot-size model. Das and Maiti (2012) formulated an inventory model for production problem and used the simulated methodology to obtain the optimal quantity under uncertainty. Rafiei et al. (2013) constructed supply chain network design as a mixed integer programming problem and minimizes the expected cost of transhipment. Roy et al. (2013) considered a deterministic situation in EOQ model with the assumption of tolerable postponement in expenses. Chakrabortty et al. (2013) discussed an inventory model in which different inventory costs and demand quantity considered as fuzzy numbers. They used intuitionistic fuzzy programming technique with different types of membership functions to obtain the Pareto optimal solution. The same work has been extended by Bhaya et al. (2014) by considering scrap and reworkable types of deficient quality items. De et al. (2014) developed an intuitionistic fuzzy optimization algorithm for solving certain and uncertain inventory model where all the parameters of an uncertain model considered as fuzzy triangular numbers. Fattahi et al. (2015) determined the reorder level and ordering quantity by optimising total cost and service level simultaneously using Metaheuristic approach. Du et al. (2015) developed a multi-objective optimisation technique based neural network model to optimise inventory costs, and the non-dominated algorithm has been used to solve it. The most notable work using multi-criterion decision making in inventory management was given by Dutta and Kumar (2013, 2015). They considered multi-products without shortages and formulated the problem as a multi-objective inventory model with conflicting linear and fractional objective function respectively and obtained the optimal order quantity of products. Some other remarkable works related to inventory control management are as follows: Xu and Zhao (2008, 2010), Wee et al. (2009), Shah and Soni (2011), Pando et al. (2012, 2013), Min et al. (2012), Bera et al. (2012), Taleizadeh et al. (2013), Tripathi (2013), Mondal et al. (2013), Mahata and Goswami (2013), Yang (2014), Srivastav and Agrawal (2016), Garai et al. (2018) and the contribution has been summarized in Table 1.

Table 1 Summary of related literature

De and Sana (2014) developed different optimization models for inventory management, the general optimization model for inventory and intuitionistic fuzzy optimization model for inventory. The primary purpose of the study is to control the regular and overtime production quantity lot under some capacitated restrictions by minimizing inventory cost function. Garg (2015a, b) formulated an inventory model to optimize the annual inventory cost of the system under a fuzzy environment in which the reorder level follows the different types of probability distributions namely uniform, exponential and Laplace distribution. Garai et al. (2015) introduced a non-linear inventory model of geometric programming with the main objective to optimize the total cost of the system with budget restriction under fuzzy intuitionistic environment. Rani et al. (2016) developed an algorithm for obtaining the Pareto optimal solution for parabolic multi-objective non-linear transportation and manufacturing problem. The main contribution of this study was the development of optimistic and pessimistic models in the intuitionistic fuzzy set environment by considering membership as well as non-membership function for these problems.

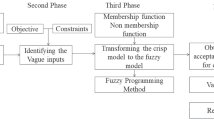
In this paper, we are formulating inventory management problem as multi-objective linear fractional inventory problem (MOLFIP) with conflicting objective functions, where our aim to optimize the profit per-ordered quantity and holding cost per-ordered quantity respectively. Also, we consider a situation in which somehow the information about some of the parameters, i.e., holding cost, purchasing price, selling price, demand and ordering cost are not precisely known but available with vagueness. After studying the pattern of vagueness, IFN used to present all these parameters in the formulated problem. The ranking method is used for the conversion of intuitionistic fuzzy parameters into an equivalent crisp form. Finally, the FGP technique is used to solve the MOLFIP to obtain best compromise order quantity. Whereas, the fuzzy goals of MOLFIP determine the individual optimum solution. These goals categorised by their accompanying membership functions which renovated into fuzzy flexible membership goals using over and under deviational variable. The main contribution of this paper can be summarized below:

• Inventory management problem has been formulated as a multi-criterion decision-making problem with conflicting fractional objective functions.

• The problem has been formulated in the intuitionistic fuzzy environment.

• Two separate models have been presented and discussed with linear and non-linear membership functions.

• Different solution sets have been generated at different discrete values of $\alpha$ and $\beta$.

The continuing part of the article includes the formulation of MOLFIP with IFN in Sect. 2. The FGP methodology with some advancement developed in Sect. 3. Section 3 presents a numerical case study which is given to demonstrate the models. Finally, Sect. 5 is devoted to a conclusion.

2 Multi-objective linear fractional inventory problem

Inventories deal with maintaining sufficient stock of goods that will ensure a smooth operation of a production system or a business activity. Traditionally, inventory has been viewed by business and industry as a necessary evil. Too little inventory may cause a costly interruption in the operation of the system, and too much of inventory can ruin the competitive edge and profitability of the business. Dutta and Kumar (2013) formulated multi-objective linear fractional inventory model, wherein they considered a hypothetical system for the inventory model with deterministic parameters. Here, we have examined the modelling and optimisation of a multi-objective linear fractional inventory model, as advanced with some imprecise information considered on it, which is represented by an IFN.

The following notations and assumptions which have used in the formulation of the problem taken from Dutta and Kumar (2013):

Nomenclature

n	Number of items i = 1, 2, 3,…, n
k	Stable cost per demand
B	Total offered budget for all items
F	Total accessible space for all items
Q i	Ordering quantity of item i
h i	Holding cost per item per unit time for ith item
P i	Purchasing price of ith item
S i	Selling Price of ith item
D i	Demand quantity per unit time of ith item
f i	Space required per unit for the ith item
OC i	Ordering cost of ith item

The following assumptions which are essential for the inventory problem have been considered as:

• 1. An inventory model with multi-items.

• 2. Infinite time horizon with one period of the cycle time.

• 3. Constant demand rate.

• 4. Lead time is zero.

• 5. Holding cost and purchase price is supposed to be known and persistent.

• 6. No discount is offered.

• 7. Shortages are not permitted.

• 8. No deterioration is permissible.

Based on the above assumptions the mathematical model for the multi-objective linear fractional inventory model for one period of the cycle time is formulated as follows:

MODEL(1)

$$\begin{aligned} {\text{Maximize}}\,\,\, & Z_{1} = \frac{{\sum_{i = 1}^{n} {(S_{i} - P_{i} )\,Q_{i} } }}{{\sum_{i = 1}^{n} {(D_{i} - Q_{i} )} }} \\ {\text{Minimize}}\,\,\, & Z_{2} = \frac{{\sum_{i = 1}^{n} {\frac{{h_{i} Q_{i} }}{2}} }}{{\sum_{i = 1}^{n} {Q_{i} } }} \\ {\text{Subject to }} & {\text{the constraint}} \\ & \sum_{i = 1}^{n} {P_{i} Q_{i} \le B} \\ & \sum_{i = 1}^{n} {f_{i} Q_{i} \le F} \\ & kD_{n} - \left( {OC_{n} } \right)Q_{n} \le 0 \\ & Q_{n} \ge 0 \quad and \quad OC_{n} > 0,\quad \forall i = 1,2,3, \ldots ,n \\ \end{aligned}$$

where

$\sum_{i = 1}^{n} {(S_{i} - P_{i} )\,Q_{i} }$ :

denotes the profit related to ordering quantity

$\sum_{i = 1}^{n} {\frac{{h_{i} Q_{i} }}{2}}$ :

denotes the holding cost

$\sum_{i = 1}^{n} {(D_{i} - Q_{i} )}$ :

denotes the back ordered quantity

$\sum_{i = 1}^{n} {Q_{i} }$ :

denotes the total ordering quantity

$\sum_{i = 1}^{n} {\frac{{kD_{n} }}{{Q_{n} }}}$ :

denotes the ordering cost

and

• Constraint I denotes the upper limit of the total investment.

• Constraint II denotes restriction on the warehouse spacing.

• Constraint III denotes the budgetary constraint on ordering cost. Ordering cost for the nth item can express as:

• 1st Item $\frac{{kD_{1} }}{{Q_{1} }} \le OC_{1} = > kD_{1} - \left( {OC_{1} } \right)Q_{1} \le 0$

• 2nd Item $\frac{{kD_{2} }}{{Q_{2} }} \le OC_{2} = > kD_{2} - \left( {OC_{2} } \right)Q_{2} \le 0$

Similarly, for the nth item

$$\frac{{kD_{n} }}{{Q_{n} }} \le OC_{n} = > kD_{n} - \left( {OC_{n} } \right)Q_{n} \le 0$$

The above-formulated model (1) extended by making some more additional assumptions, which are as follows:

• Holding Cost cannot be fixed in advance, and it may vary over time-period.

• Purchasing Price and Selling price cannot be uniform respectively for the different zones and time periods. It can vary from these two factors.

• The demand for the items cannot prefix in advanced. It may always vary due to the behaviours of customers’ requirements.

• The ordering cost cannot also be prefixed. It is also an independent factor of human behaviour. So it can also vary from the predetermined fixed cost.

Therefore, all these parameters that are holding cost, purchasing price, selling price, demand and ordering cost which are not precisely known to the decision maker. However, somehow the information about all these parameters is available with vagueness. We have considered that IFN’s can present this vagueness in the parameters. Hence model (1), can be rewritten after amendments all these above assumptions as follows:

MODEL (2)

$$\begin{aligned} {\text{Maximize}}\quad & \tilde{Z}_{1} = \frac{{\sum_{i = 1}^{n} {(\tilde{S}_{i}^{I} - \tilde{P}_{i}^{I} )\,Q_{i} } }}{{\sum_{i = 1}^{n} {(\tilde{D}_{i}^{I} - Q_{i} )} }} \\ {\text{Minimize}}\quad & \tilde{Z}_{2} = \frac{{\sum_{i = 1}^{n} {\frac{{\tilde{h}_{i}^{I} Q_{i} }}{2}} }}{{\sum_{i = 1}^{n} {Q_{i} } }} \\ {\text{Subject to }} & {\text{the constraints}} \\ & \sum_{i = 1}^{n} {\tilde{P}_{i}^{I} Q_{i} \le B} , \\ & \sum_{i = 1}^{n} {f_{i} Q_{i} \le F,} \\ & kD_{n} - (\widetilde{{OC_{n} }})^{I} \le 0\,\,\,\left( {{\text{for each}}\,\,n} \right), \\ & {\text{and all}}\,\,\,Q_{n} \ge 0 \\ \end{aligned}$$

We assume that $\tilde{S}_{i}^{I} ,\tilde{P}_{i}^{I} ,\tilde{h}_{i}^{I} ,\tilde{D}_{i}^{I}$ and $(\widetilde{{OC_{n} }})^{I}$ are IFN for each $i = 1,2, \ldots ,n$.

The preliminaries of IFN’s and their ranking function has been studied from Atanassov (1986, 1989), Singh and Yadav (2016). In Model (2), the following input information namely selling price, purchasing price, holding cost, ordering cost and demand of items have been assuming as IFN and follows the following definitions, which are given below.

Definition 1

(IFN) An intuitionistic fuzzy set $\tilde{S}_{i}^{I} = \{ < x,\mu_{{\tilde{S}_{i}^{I} }} (x),\gamma_{{\tilde{S}_{i}^{I} }} (x) > \,\,:\,x \in X\}$ called an IFN if the following situation holds:

• 1. If there exists $m \in R$ such that $\mu_{{\tilde{S}_{i}^{I} }} (m) = 1\,$ and $\gamma_{{\tilde{S}_{i}^{I} }} (m) = 0\,$ (m is known as the mean value of $\tilde{S}_{i}^{I})$.

• 2. If $\mu_{{\tilde{S}_{i}^{I} }} \,$ and $\gamma_{{\tilde{S}_{i}^{I} }}$ area continuous function from R to the closed [0, 1] and $0 \le \mu_{{\tilde{S}_{i}^{I} }} (x) + \gamma_{{\tilde{S}_{i}^{I} }} \,(x) \le 1,\,\,\forall x \in R,$ where

$$\mu_{{\tilde{S}_{i}^{I} }} \,(x) = \left\{ {\begin{array}{ll} {g_{1} (x),} \hfill &\quad {m - a_{{S_{i} }} \le x < m} \hfill \\ {1,} \hfill & \quad{x = m} \hfill \\ {h_{1} (x),} \hfill & \quad{m < x \le m + b_{{S_{i} }} } \hfill \\ {0,} \hfill & \quad{otherwise} \hfill \\ \end{array} } \right.$$

and

$$\gamma_{{\tilde{S}_{i}^{I} }} \,(x) = \left\{ {\begin{array}{ll} {g_{2} (x),} \hfill & \quad{m - a_{{S_{i} }}^{\prime} \le x < m;\,\,0 \le g_{1} (x) + g_{2} (x) \le 1} \hfill \\ {1,} \hfill &\quad {x = m} \hfill \\ {h_{2} (x),} \hfill &\quad {m < x \le m + b_{{S_{i} }}^{'} ;\,\,0 \le h_{1} (x) + h_{2} (x) \le 1} \hfill \\ {0,} \hfill &\quad {otherwise} \hfill \\ \end{array} } \right.$$

Here m is the average value of IFN $\tilde{S}_{i}^{I}$; $(a_{{S_{i} }} ,b_{{S_{i} }} )$ and $(a_{{S_{i} }}^{\prime} ,b_{{S_{i} }}^{\prime} )$ are the left and right spreads of the linear membership function (LMF) $\mu_{{\tilde{S}_{i}^{I} }} (x)\,$ and non-linear membership function NLMF $\gamma_{{\tilde{S}_{i}^{I} }} (x)\,,$ respectively. The symbols g₁ and h₁ are piecewise continuous, strictly increasing, and strictly decreasing functions in [$m - a_{{S_{i} }} ,m$) and ($m,m + b_{{S_{i} }}$], strictly decreasing, and strictly increasing functions in [$m - a_{{S_{i} }}^{\prime} ,m$] and [$m,m + b_{{S_{i} }}^{\prime}$], respectively. Therefore, the IFN can define as $\tilde{S}_{i}^{I} = (m;a_{{S_{i} }} ,b_{{S_{i} }} ;a_{{S_{i} }}^{\prime} ,b_{{S_{i} }}^{\prime} ).$

Definition 2

(Triangular IFN) Let us assume that $\tilde{S}_{i}^{I} = \{ (a_{{S_{i} }} ,b_{{S_{i} }} ,c_{{S_{i} }} )\,;(e_{{S_{i} }} ,b_{{S_{i} }} ,f_{{S_{i} }} )\} ,$$\forall \,e_{{S_{i} }} \le a_{{S_{i} }} \le b_{{S_{i} }} \le c_{{S_{i} }} \le f_{{S_{i} }}$ be a triangular IFN with LMF $\mu_{{\tilde{S}_{i}^{I} }} \,$ and NLMF $\gamma_{{\tilde{S}_{i}^{I} }}$ which is given as:

$$\mu_{{\tilde{S}_{i}^{I} }} \,(x) = \left\{ {\begin{array}{ll} {\frac{{x - a_{{S_{i} }} }}{{b_{{S_{i} }} - a_{{S_{i} }} }},} \hfill &\quad {a_{{S_{i} }} < x \le b_{{S_{i} }} } \hfill \\ {1,} \hfill & \quad{x = b_{{S_{i} }} } \hfill \\ {\frac{{c_{{S_{i} }} - x}}{{c_{{S_{i} }} - b_{{S_{i} }} }},} \hfill &\quad {b_{{S_{i} }} \le x \le c_{{S_{i} }} } \hfill \\ {0,} \hfill &\quad {otherwise} \hfill \\ \end{array} } \right.$$

(1)

and

$$\gamma_{{\tilde{S}_{i}^{I} }} \,(x) = \left\{ {\begin{array}{ll} {\frac{{b_{{S_{i} }} - x}}{{b_{{S_{i} }} - e_{{S_{i} }} }},} \hfill &\quad {e_{{S_{i} }} < x \le b_{{S_{i} }} } \hfill \\ {1,} \hfill &\quad {x = b_{{S_{i} }} } \hfill \\ {\frac{{x - b_{{S_{i} }} }}{{f_{{S_{i} }} - b_{{S_{i} }} }},} \hfill &\quad {b_{{S_{i} }} \le x < f_{{S_{i} }} } \hfill \\ {0,} \hfill & \quad{otherwise} \hfill \\ \end{array} } \right.$$

(2)

The left and right bound of the triangular IFN at $(\alpha ,\beta )$ set with its LMF and NLMF can express as:

$$\begin{aligned} & L_{{\mu_{{S_{i} }} }} (x) = \frac{{x - a_{{S_{i} }} }}{{b_{{S_{i} }} - a_{{S_{i} }} }},\quad a_{{S_{i} }} \le x \le b_{{S_{i} }} \quad {\text{and}}\quad R_{{\mu_{{S_{i} }} }} (x) = \frac{{c_{{S_{i} }} - x}}{{c_{{S_{i} }} - b_{{S_{i} }} }},\quad b_{{S_{i} }} \le x \le c_{{S_{i} }} \\ & L_{{\gamma_{{S_{i} }} }} (x) = \frac{{b_{{S_{i} }} - x}}{{b_{{S_{i} }} - e_{{S_{i} }} }},\quad e_{{S_{i} }} \le x \le b_{{S_{i} }} \quad {\text{and}}\quad R_{{\gamma_{{S_{i} }} }} (x) = \frac{{x - b_{{S_{i} }} }}{{f_{{S_{i} }} - b_{{S_{i} }} }},\quad b_{{S_{i} }} \le x \le f_{{S_{i} }} \\ \end{aligned}$$

The inverse function $L^{ - 1}$ and $R^{ - 1}$ can define analytically as

$$\begin{aligned} L_{{\mu_{{S_{i} }} }}^{ - 1} (h) & = a_{{S_{i} }} + (b_{{S_{i} }} - a_{{S_{i} }} )h,\quad R_{{\mu_{{S_{i} }} }}^{ - 1} (h) = c_{{S_{i} }} - (c_{{S_{i} }} - b_{{S_{i} }} )h \\ L_{{\gamma_{{S_{i} }} }}^{ - 1} (h) & = b_{{S_{i} }} - (b_{{S_{i} }} - e_{{S_{i} }} )h,\quad R_{{\gamma_{{S_{i} }} }}^{ - 1} (h) = b_{{S_{i} }} + (f_{{S_{i} }} - b_{{S_{i} }} )h \\ \end{aligned}$$

The magnitude of LMF for $\tilde{S}_{i}^{I}$ at $\alpha$ level can express as:

$$\begin{aligned} P_{{\mu_{{S_{i} }} }} (\tilde{S}_{i}^{I} ) & = \frac{{\int\limits_{0}^{1} {h\left[ {\alpha \left( {a_{{S_{i} }} + (b_{{S_{i} }} - a_{{S_{i} }} )h} \right) + (1 - \alpha )\left( {c_{{S_{i} }} - (c_{{S_{i} }} - b_{{S_{i} }} )h} \right)} \right]dh} }}{{\int\limits_{0}^{1} {h\,dh} }} \\ & = \frac{{\left[ {\frac{{a_{{S_{i} }} \alpha h^{2} }}{2} + \frac{{\alpha (b_{{S_{i} }} - a_{{S_{i} }} )h^{3} }}{3} + \frac{{(1 - \alpha )c_{{S_{i} }} h^{2} }}{2} - \frac{{(1 - \alpha )(c_{{S_{i} }} - b_{{S_{i} }} )h^{3} }}{3}} \right]_{0}^{1} }}{{\left[ {\frac{{h^{2} }}{2}} \right]_{0}^{1} }} \\ & = \frac{{\alpha (a_{{S_{i} }} - c_{{S_{i} }} ) + c_{{S_{i} }} + 2b_{{S_{i} }} }}{3} \\ \end{aligned}$$

(3)

The magnitude of NLMF for $\tilde{S}_{i}^{I}$ at $\beta$ level can express as:

$$\begin{aligned} P_{{\gamma_{{S_{i} }} }} (\tilde{S}_{i}^{I} ) & = \frac{{\int\limits_{0}^{1} {h\left[ {\beta \left( {b_{{S_{i} }} - (b_{{S_{i} }} - e_{{S_{i} }} )h} \right) + (1 - \beta )\left( {b_{{S_{i} }} + (f_{{S_{i} }} - b_{{S_{i} }} )h} \right)} \right]dh} }}{{\int\limits_{0}^{1} {h\,dh} }} \\ & = \frac{{\left[ {\frac{{\beta b_{{S_{i} }} h^{2} }}{2} - \frac{{\beta (b_{{S_{i} }} - e_{{S_{i} }} )h^{3} }}{3} + \frac{{(1 - \beta )b_{{S_{i} }} h^{2} }}{2} + \frac{{(1 - \beta )(f_{{S_{i} }} - b_{{S_{i} }} )h^{3} }}{3}} \right]_{0}^{1} }}{{\left[ {\frac{{h^{2} }}{2}} \right]_{0}^{1} }} \\ & = \frac{{2\beta (e_{{S_{i} }} - f_{{S_{i} }} ) + b_{{S_{i} }} + 2f_{{S_{i} }} }}{3} \\ \end{aligned}$$

(4)

The magnitude of LMF and NLMF for $\tilde{S}_{i}^{I}$ at $(\alpha ,\beta )$ level can express as:

$$P(\tilde{S}^{I} ) = \left[ {\frac{{\alpha (a_{{S_{i} }} - c_{{S_{i} }} ) + c_{{S_{i} }} + 2b_{{S_{i} }} }}{3},\frac{{2\beta (e_{{S_{i} }} - f_{{S_{i} }} ) + b_{{S_{i} }} + 2f_{{S_{i} }} }}{3}} \right]$$

Similarly, the same assumption followed for the other intuitionistic fuzzy parameters, i.e., ($\tilde{P}_{i}^{I} ,\tilde{h}_{i}^{I} ,\tilde{D}_{i}^{I}$, $(\widetilde{{OC_{n} }})^{I}$) respectively. Based on the above conversion procedures of IFN; the model (2) has been rewritten as:

MODEL (2A)

$$\begin{aligned} {\text{Maximize}}\quad & \tilde{Z}_{1} = \frac{{\sum_{i = 1}^{n} {\left( {\frac{{\alpha (a_{{S_{i} }} - c_{{S_{i} }} ) + c_{{S_{i} }} + 2b_{{S_{i} }} }}{3} - \frac{{\alpha (a_{{P_{i} }} - c_{{P_{i} }} ) + c_{{P_{i} }} + 2b_{{P_{i} }} }}{3}} \right)\,Q_{i} } }}{{\sum_{i = 1}^{n} {\left( {\frac{{\alpha (a_{{D_{i} }} - c_{{D_{i} }} ) + c_{{D_{i} }} + 2b_{{D_{i} }} }}{3} - Q_{i} } \right)} }} \\ {\text{Minimize}}\quad & \tilde{Z}_{2} = \frac{{\sum_{i = 1}^{n} {\frac{{\left( {\alpha (a_{{h_{i} }} - c_{{h_{i} }} ) + c_{{h_{i} }} + 2b_{{h_{i} }} } \right)Q_{i} }}{6}} }}{{\sum_{i = 1}^{n} {Q_{i} } }} \\ {\text{Subject to }} & {\text{the constraints}} \\ & \sum_{i = 1}^{n} {\left( {\frac{{\alpha (a_{{P_{i} }} - c_{{P_{i} }} ) + c_{{P_{i} }} + 2b_{{P_{i} }} }}{3}} \right)Q_{i} \le B} , \\ \end{aligned}$$

(5)

$$\sum_{i = 1}^{n} {f_{i} Q_{i} \le F,}$$

(6)

$$k\,D_{n} - \left( {\frac{{\alpha (a_{{OC_{n} }} - c_{{OC_{n} }} ) + c_{{OC_{n} }} + 2b_{{OC_{n} }} }}{3}} \right) \le 0\quad \left( {{\text{for each}}\,\,n} \right),$$

(7)

$${\text{and all}}\,\,\,\,\,Q_{n} \ge 0$$

(8)

Similarly, an equivalent crisp form of MODEL(2) with NLMF expressed as follows:

MODEL (2B)

$$\begin{aligned} {\text{Maximize}}\quad & \tilde{Z}_{1} = \frac{{\sum_{i = 1}^{n} {\left( {\frac{{2\beta (e_{{S_{i} }} - f_{{S_{i} }} ) + b_{{S_{i} }} + 2f_{{S_{i} }} }}{3} - \frac{{2\beta (e_{{P_{i} }} - f_{{P_{i} }} ) + b_{{P_{i} }} + 2f_{{P_{i} }} }}{3}} \right)\,Q_{i} } }}{{\sum_{i = 1}^{n} {\left( {\frac{{2\beta (e_{{D_{i} }} - f_{{D_{i} }} ) + b_{{D_{i} }} + 2f_{{D_{i} }} }}{3} - Q_{i} } \right)} }} \\ {\text{Minimize}}\quad & \tilde{Z}_{2} = \frac{{\sum_{i = 1}^{n} {\frac{{\left( {2\beta (e_{{h_{i} }} - f_{{h_{i} }} ) + b_{{h_{i} }} + 2f_{{h_{i} }} } \right)Q_{i} }}{6}} }}{{\sum_{i = 1}^{n} {Q_{i} } }} \\ \end{aligned}$$

Subject to the constraints

$$\sum_{i = 1}^{n} {\left( {\frac{{2\beta (e_{{P_{i} }} - f_{{P_{i} }} ) + b_{{P_{i} }} + 2f_{{P_{i} }} }}{3}} \right)Q_{i} \le B} ,$$

(9)

$$\sum_{i = 1}^{n} {f_{i} Q_{i} \le F,}$$

(10)

$$k\,D_{n} - \frac{{2\beta (e_{{OC_{n} }} - f_{{OC_{n} }} ) + b_{{OC_{n} }} + 2f_{{OC_{n} }} }}{3}\quad \left( {{\text{for each}}\,\,\,n} \right),$$

(11)

$${\text{and all}}\,\,Q_{n} \ge 0$$

(12)

3 Fuzzy goal programming approach

FGP is a powerful and flexible technique that can apply to a variety of decision-making problems involving multiple objectives. Several contributions have been reported in the literature on FGP approach. In all these literature efficient methodologies has been developed for solving multi-objective programming problems employing the FGP approach. After doing some manipulations in FGP approach, we have given a stepwise solution procedure for solving the formulated MOLFIP.

3.1 Procedure for solving molfip

This stepwise solution procedure of FGP has been used to obtain the optimal order quantity in an intuitionistic fuzzy environment, which are as follows:

• Step 1 Formulate the inventory problem as MOLFIP with certain and uncertain parameters (holding cost, purchasing price, selling price, demand and ordering cost).

• Step 2 As explained in Sect. 2, the first step is to convert the intuitionistic fuzzy parameters of MOLFIP into the equivalent crisp form using the ranking procedure. The equivalent crisp form for MODEL (2A) of MOLFIP in which IFN is in the shape of LMF has obtained by using Eq. (3). Similarly, the case when the IFN is in the form of the NLMF, the resultant equivalent crisp form for the MODEL (2B) of MOLFIP has obtained by using Eq. (4).

• Step 3 Here we have two resultant crisp form models of MOLFIP, i.e., MODEL (2A) and MODEL (2B). Firstly the MODEL (2A) is solved as a solitary objective problem using only one objective at a time for different values of $\alpha \in \left[ {0,1} \right]$ and ignoring the other objective functions.

Similarly, MODEL (2B) is solved as a solitary objective problem using only one objective at a time for the different values of $\beta \in \left[ {0,1} \right]$ and ignoring the other objective functions. The solutions thus obtained of these models are considered to be ideal solutions and these solutions help to the decision maker for setting the aspiration level to each of the objective function.

• Step 4 The aspiration level to each of the objective functions, $\tilde{Z}_{j} (x),\,j = 1,2$ of the models can define in such a way.

Now MOLFIP (2A) is defined as follows:

$$\begin{aligned} \tilde{Z}_{1} (X)\,\,\,\underline{ \succ } \,\,g_{1} , &\quad ( {\text{fuzzy}} - {\text{max)}} \hfill \\ \tilde{Z}_{2} (X)\,\,\,\underline{ \prec } \,\,g_{2} , &\quad ( {\text{fuzzy}} - {\text{min)}} \hfill \\ \end{aligned}$$

(13)

Subject to Constraint (5)–(8)

Where $\left( {g_{1} } \right)_{\alpha } = Max\,\,\left( {Z_{1} (x)} \right)_{\alpha }$ and $(g_{2} )_{\alpha } = Min\,\left( {Z_{2} (x)} \right)_{\alpha } \,$$\forall \,\alpha \in [0,1]$.

Solved the Eq. (13) by achieving all its defined fuzzy goals and for the optimal values $Q_{i} * = (Q_{1} ,Q_{2} , \ldots ,Q_{n} )$.

Similarly, MOLFIP (2B) is defined as follows:

$$\begin{aligned} \tilde{Z}_{1} (X)\,\,\,\underline{ \succ } \,\,g_{1} , &\quad ( {\text{fuzzy}} - {\text{max)}} \hfill \\ \tilde{Z}_{2} (X)\,\,\,\underline{ \prec } \,\,g_{2} , &\quad ( {\text{fuzzy}} - {\text{min)}} \hfill \\ \end{aligned}$$

(14)

Subject to Constraint (9)–(12)

Where $\left( {g_{1} } \right)_{\beta } = Max\,\,\left( {Z_{1} (x)} \right)_{\beta }$ and $(g_{2} )_{\beta } = Min\,\left( {Z_{2} (x)} \right)_{\beta } \,$$\forall \,\beta \in [0,1]$.

Similarly, Solved the Eq. (14) by achieving all its defined fuzzy goals and for the optimal values $Q_{{}} * = (Q_{1} ,Q_{2} , \ldots ,Q_{n} )$.

Step 5 Construct a fuzzy linear membership function for the Model (2A) for both the defined objective functions. Hence, the membership function of the fuzzy goal $\tilde{Z}_{1} (X)\,\,\underline{ \succ } \,g_{1}$ (i.e., fuzzy-max) is defined as:

$$\mu_{1} (\tilde{Z}_{1} (X)) = \left\{ {\begin{array}{ll} {1,} \hfill &\quad {if\,\,\tilde{Z}_{1} (X) \ge g_{1} } \hfill \\ {\frac{{\tilde{Z}_{1} (X) - L_{1} }}{{g_{1} - L_{1} }},} \hfill & \quad{if\,\,L_{1} \le \tilde{Z}_{1} (X) \le g_{1} } \hfill \\ {0,} \hfill &\quad {if\,\,\tilde{Z}_{1} (X) \le L_{1} } \hfill \\ \end{array} } \right.$$

where $\,L_{1}$ is the lower tolerance limit of the fuzzy goal, $\,\tilde{Z}_{1} (x)$ (Fig. 1).

Fig. 1

Linear membership function $(\tilde{Z}_{1} (X)\,\,\underline{ \succ } \,g_{1} )$

Moreover, similarly, for the fuzzy goal $\,\tilde{Z}_{2} \,\underline{ \prec } \,\,g_{2}$ (i.e., fuzzy-min), the membership function is defined as:

$$\mu_{2} (\tilde{Z}_{2} (X)) = \left\{ {\begin{array}{ll} {1,} \hfill &\quad {if\,\,\tilde{Z}_{2} (X) \le g_{2} } \hfill \\ {\frac{{U_{2} - \tilde{Z}_{2} (X)}}{{U_{2} - g_{2} }},} \hfill &\quad {if\,\,g_{2} \le \tilde{Z}_{2} (X) \le U_{2} } \hfill \\ {0,} \hfill &\quad {if\,\,\tilde{Z}_{2} (X) \ge U_{2} } \hfill \\ \end{array} } \right.$$

where $U_{2} \,\,$ is the upper tolerance limit of the fuzzy goal $\,\tilde{Z}_{2} (x)$ (Fig. 2).

Fig. 2

Linear membership function $(\tilde{Z}_{2} (X)\,\,\underline{ \prec } \,\,g_{2} )$

It has been known that the possible highest degree of membership function can only be unity in fuzzy programming. Therefore, the flexible membership goals with the aspiration level can define as:

$$\begin{aligned} & \frac{{\tilde{Z}_{1} (X) - L_{1} }}{{g_{1} - L_{1} }} + d_{1}^{ - } - d_{1}^{ + } = 1, \\ & \frac{{U_{2} - \tilde{Z}_{2} (X)}}{{U_{2} - g_{2} }} + d_{2}^{ - } - d_{2}^{ + } = 1, \\ \end{aligned}$$

where $d_{j}^{ - } \ge 0,\,\,\,d_{j}^{ + } \ge 0,\,\,j = 1,2$ with $d_{j}^{ + } d_{j}^{ - } = 0,\,\,j = 1,2$ are respectively under- and over-deviations from the targeted goal. Similarly, the same procedure has been followed for construction of membership function for Model (2B).

Step 6 Calculate the weight which is attached to both the objective function:

$$\begin{aligned} & w_{1} = \frac{1}{{g_{1} - l_{1} }}\quad for\,\,\hbox{max} - fuzzy\,\,goal \\ & w_{2} = \frac{1}{{u_{2} - g_{2} }}\quad for\,\,\hbox{min} - fuzzy\,\,goal \\ \end{aligned}$$

Similarly, the same weighted criterion has been used for the Model (2B).

Step 7 By following all the above-given steps, FGP model for MOLFIP is formulated as follows:

$$\begin{aligned} Min\quad & \sum_{j = 1}^{2} {w_{j} d_{j}^{ - } } \\ subject & \,\,to\,\,\,{\text{the}}\,\,{\text{constraints}}\, ( 9 )\,\,t{\text{o}}\,\, ( 1 2 )\,{\text{of model 2(A)}}\,\, \\ {\text{and}}\quad & \frac{{\tilde{Z}_{1} (X) - L_{1} }}{{g_{1} - L_{1} }} + d_{1}^{ - } - d_{1}^{ + } = 1, \\ & \frac{{U_{2} - \tilde{Z}_{2} (X)}}{{U_{2} - g_{2} }} + d_{2}^{ - } - d_{2}^{ + } = 1, \\ & d_{j}^{ - } ,d_{j}^{ + } \ge 0,\,\,with\,\,\,\,\,d_{j}^{ - } \times d_{j}^{ + } = 0,\,j = 1,2 \\ & Q_{n} \ge 0 \\ \end{aligned}$$

(15)

A similar model has been formulated for Model (2B) with some others additional set of constraints (13)–(16) in place of the set of constraints (9)–(12). Finally, the above-formulated problem has been solving to obtain the optimal compromise solution $Q^{*}$ by using the optimising software LINGO 16.0. If the decision maker is not satisfied with the solution, then proceed to step 8.

Step 8 Construct the membership functions for the decision vector $Q_{{}}^{*} = (Q_{1} ,Q_{2} , \ldots ,Q_{n} ).$

Let $t^{L} \,\,{\text{and}}\,\,t^{R}$ are the maximum negative and maximum positive tolerance values, which are not necessarily to be the same. This tolerance value helps the DM to extend the feasible region to search for the optimal solution. In the case of no feasible region, this tolerance limits can increase for searching the new feasible region in which the desired optimal solution can found (Fig. 3).

Fig. 3

Membership function of decision vector

The linear membership function of controlled decision vector can be defined as follows:

$$\mu (Q_{n} ) = \left\{ {\begin{array}{ll} {\frac{{Q_{n} - (Q_{{_{n} }}^{*} - t^{L} )}}{{t^{L} }},} \hfill &\quad {if\,\,Q_{n}^{*} - t^{L} \le Q_{n} \le Q_{n}^{*} } \hfill \\ {\frac{{(Q_{n}^{*} + t^{R} ) - Q_{n} }}{{t^{R} }},} \hfill &\quad {if\,\,Q_{n}^{*} \le Q_{n} \le Q_{n}^{*} + t^{R} } \hfill \\ {0,} \hfill &\quad {if\,\,otherwise} \hfill \\ \end{array} } \right.$$

where $Q_{{}}^{*}$ is the most preferred solution. The satisfaction level of $Q_{n}^{*}$ is linearly increasing in the interval $\left[ {Q_{n}^{*} - t^{L} ,Q_{n} } \right]$, and linearly decreasing in the interval $\left[ {Q_{n} ,Q_{n}^{*} + t^{L} } \right]$.

So, for the defined membership function of the decision vector, the flexible membership goals with aspiration levels are can be expressed as follows:

$$\mu (Q_{n} ) + d_{n}^{ - } - d_{n}^{ + } = 1,$$

Alternatively, equivalently as

$$\begin{aligned} & \frac{{Q_{n} - (Q_{n}^{*} - t^{L} )}}{{t^{L} }} + d_{n}^{L - } - d_{n}^{L + } = 1 \\ & \frac{{(Q_{n}^{*} + t^{R} ) - Q_{k} }}{{t^{R} }} + d_{n}^{R - } - d_{n}^{R + } = 1 \\ \end{aligned}$$

where $d_{n}^{ - } = (d_{n}^{L - } ,d_{n}^{R - } )$, $d_{n}^{ + } = (d_{n}^{L + } ,d_{n}^{R + } )$ and $d_{n}^{L - } ,d_{n}^{R - } ,d_{n}^{L + } ,d_{n}^{R + } \ge 0$ with $d_{n}^{L - } \times d_{n}^{L + } = 0$ and $d_{n}^{R - } \times d_{n}^{R + } = 0$, respectively, represents the under-deviational and over-deviational from the targeted goals. Calculation of weights $w_{n}^{L} \,\,{\text{and}}\,\,\,w_{n}^{R}$ attached to the decision variables is as follows:

$$w_{n}^{L} = \frac{1}{{t^{L} }}\quad {\text{and}}\quad \,\,\,w_{n}^{R} = \frac{1}{{t^{R} }}$$

Similarly, the same procedure will follow for construction of membership function for Model (2B).

Step 9 By following all the above steps, final FGP model for MOLFIP has been formulated as follows:

$$\begin{aligned} Min\quad & \sum_{j = 1}^{2} {w_{j} d_{j}^{ - } } + \sum_{n = 1}^{3} {[w_{n}^{L} (d_{n}^{L - } + d_{n}^{L + } ) + w_{n}^{R} (d_{n}^{R - } + d_{n}^{R + } )]} \\ subject & \,\,to\,\,\,{\text{the}}\,\,{\text{constraint}}\, ( 9 )\,\,t{\text{o}}\,\, ( 1 2 )\,{\text{of model 2(A)}}\,\, \\ {\text{and}}\quad & \frac{{\tilde{Z}_{1} (X) - L_{1} }}{{g_{1} - L_{1} }} + d_{1}^{ - } - d_{1}^{ + } = 1, \\ & \frac{{U_{2} - \tilde{Z}_{2} (X)}}{{U_{2} - g_{2} }} + d_{2}^{ - } - d_{2}^{ + } = 1, \\ & \frac{{Q_{n} - (Q_{n}^{*} - t^{L} )}}{{t^{L} }} + d_{n}^{L - } - d_{n}^{L + } = 1 \\ & \frac{{(Q_{n}^{*} + t^{R} ) - Q_{k} }}{{t^{R} }} + d_{n}^{R - } - d_{n}^{R + } = 1 \\ & d_{j}^{ - } ,d_{j}^{ + } \ge 0,\,\,with\,\,\,\,\,d_{j}^{ - } \times d_{j}^{ + } = 0,\,j = 1,2 \\ & d_{n}^{L - } ,d_{n}^{L + } \ge 0,\,\,with\,\,d_{n}^{L - } \times d_{n}^{L + } = 0 \\ & d_{n}^{R - } ,d_{n}^{R + } \ge 0,\,\,with\,\,\,d_{n}^{R - } \times d_{n}^{R + } = 0 \\ & Q_{n} \ge 0 \\ \end{aligned}$$

(16)

A similar model has been formulated for Model (2B) with some others additional set of constraints (13)–(16) in place of the set of constraints (9)–(12). Finally, the above-formulated problem has been solved to obtain the optimal compromise solution $Q^{*}$ by using the optimising software LINGO 16.0 (Fig. 4).

Fig. 4

Flowchart of solution methodology

4 Numerical example

The following numerical example has been used to illustrate the proposed approach. Dutta and Kumar (2013) have presented their inventory model with fixed input information data set. Here we are considering the case of inventory optimisation problem in which the input information is available in the form of IFN. This available information is summarised in Table 2 and given below:

Table 2 Input data for a three-item inventory problem

By using the above information of Table 2 in model 2, the MOLFIP with intuitionistic fuzzy input data is expressed as:

$$\begin{aligned} Max\,Z_{1} & = \frac{{(\widetilde{650}^{I} - \widetilde{625}^{I} )Q_{1} + \left( {\widetilde{750}^{I} - \widetilde{730}^{I} } \right)Q_{2} + \left( {\widetilde{450}^{I} - \widetilde{440}^{I} } \right)Q_{3} }}{{\left( {\widetilde{1000}^{I} - Q_{1} } \right) + \left( {\widetilde{2000}^{I} - Q_{2} } \right) + \left( {\widetilde{1500}^{I} - Q_{3} } \right)}} \\ Min\,Z_{2} & = \frac{{\frac{{\widetilde{12}^{I} Q_{1} }}{2} + \frac{{\widetilde{16}^{I} Q_{1} }}{2} + \frac{{\widetilde{18}^{I} Q_{1} }}{2}}}{{Q_{1} + Q_{2} + Q_{3} }} \\ \end{aligned}$$

Subject to the constraint

$$\begin{aligned} & \widetilde{625}^{I} Q_{1} + \widetilde{730}^{I} Q_{2} + \widetilde{440}^{I} Q_{3} \le 900,000 \\ & 2Q_{1} + 4Q_{2} + 2Q_{3} \le 13,000 \\ & 7\left( {\widetilde{1000}^{I} } \right) - \widetilde{320}^{I} Q_{1} \le 0 \\ & 7\left( {\widetilde{2000}^{I} } \right) - \widetilde{350}^{I} Q_{2} \le 0 \\ & 7\left( {\widetilde{1500}^{I} } \right) - \widetilde{250}^{I} Q_{3} \le 0 \\ & All\;Q_{i} \ge 0,\;i = 1,2,3\end{aligned}$$

(17)

The Eq. (16) is in the form of fuzzy numbers. We cannot solve it directly by any given methods. Therefore first we convert it to crisp form and then will be solved. As we have discussed the two models are made for this, Model (2A) and Model (2B). Here we are debating Model (2A) under the case 1 and Model (2B) under the case 2.

Case 1 for Model (2A)

This model has been solved by followed the stepwise solution procedure as defined in Sect. 3.1. The maximum and minimum individual values of the objective function at the different value of $\alpha \in [0,1]$ has been given in Tables 3, 4, 5 and 6.

Table 3 Individual maximum solution $(Z_{1} )$

Table 4 Individual minimum solution $(Z_{1} )$

Table 5 Individual minimum solution $(Z_{2} )$

Table 6 Individual maximum solution $(Z_{2} )$

The relative weights attached to each objective functions given in Table 7.

Table 7 Relative weights

Table 8 has been obtained by using the table’s values of 3–7. Table 8 is the final solution table for the Model (2A).

Table 8 Optimal compromise objective values with order quantities

From Table 8 and Fig. 5, we have seen that at $\alpha = 0$, the optimal order quantities are as follows: Q₁ = 22.19335 units, Q₂ = 1187.256 units, Q₃ = 42.41547 units with optimal compromise value of objective functions are Z₁= 7.498250, Z₂ = 8.62294. Similarly, at $\alpha = 1.0$, the optimal order quantities are as Q₁ = 21.58310 units, Q₂ = 1190.436 units, Q₃ = 41.63432 units with optimal compromise value of objective functions are Z₁ = 7.782631, Z₂ = 8.005682. The obtained result shows that proposed approach can generates more consistent results with efficient solutions. Hence, the solutions obtained at the different value of α helps the decision maker to choose the best solution which increases or decreases according to the preference as defined in terms of weight. Specifically, α = 0 gives the widest lowest possibility, indicating that the objective value will never fall outside of this range while at the other extreme end of α  = 1, it provides the most optimistic value of the objective value. For this example, both the objective function is fuzzy intuitionistic and conflicting in nature, the most likely value of objective function are Z₁ = 7.619745, Z₂ = 8.300349, while the pessimistic value are Z₁ = 7.498250, Z₂ = 8.622942 and the optimistic value of objective function are Z₁ = 7.782631, Z₂ = 8.005682.

Fig. 5

Different values of the objective function

Case 2 for Model (2B)

In similar to Model (2A), this model has also been solved by following the stepwise solution procedure as defined in Sect. 3.1. The maximum and minimum individual values of the objective function at the different value of $\beta \in [0,1]$ has been given in Tables 9, 10, 11 and 12.

Table 9 Individual maximum solution $(Z_{1} )$

Table 10 Individual minimum solution $(Z_{1} )$

Table 11 Individual minimum solution $(Z_{2} )$

Table 12 Individual maximum solution $(Z_{2} )$

The relative weights attached to each objective functions given in Table 13.

Table 13 Relative weights

Table 14 has been obtained by using the Table’s values of 9–13. Table 14 is the final solution Table for the Model (2B).

Table 14 Optimal compromise objective values with order quantities

From the Table 14 and Fig. 6, we have seen that at $\beta = 0$, the optimal order quantity quantities are as follows: Q₁ = 23.18841 units, Q₂ = 41.09848 units, Q₃ = 1935.242 units with optimal compromise value of objective functions are Z₁ = 7.685360, Z₂ = 19.62314. Similarly, at $\beta = 1.0$, the optimal order quantities are as Q₁ = 20.54507 units, Q₂ = 38.88889 units, Q₃ = 1960.934 units with optimal compromise value of objective functions are Z₁ = 9.168477, Z₂ = 15.71491. The obtained result shows that proposed approach can generates more consistent results with efficient solutions. Hence, the solutions obtained at a different value of $\beta$ helps the decision maker to choose the best solution which increases or decreases according to the preference as defined in terms of weight. Specifically, $\beta = 0$ gives the widest lowest possibility, indicating that the objective value will never fall outside of this range while at the other extreme end of $\beta = 1.0$, it provides the most optimistic value of the objective value. For this example, both the objective function is fuzzy intuitionistic and conflicting in nature, the most likely value of objective function are Z₁ = 8.295876, Z₂ = 17.68649, while the pessimistic value are Z₁ = 7.685360, Z₂ = 19.62314 and the optimistic value of objective function are Z₁ = 9.168477, Z₂ = 15.71491. LMF focuses more on Q₂ ordered quantity while in case of NLMF focus shifted more to Q₃ ordered quantity.

Fig. 6

Different values of objective function

The above example has been compared with Dutta and Kumar (2013). They formulated the problem in deterministic environment and obtained the following results $Q_{1} = 1363.712,\,\,Q_{2} = 40,\,\,Q_{3} = 42$ with $Z_{1} = 11.5617,\,\,Z_{2} = 6.1424$.

The relative effectiveness (R.E.) of an obtained compromise solution with respect to the Dutta and Kumar (2013) approach is defined as:

$$R.E. = T_{Dutta\,and\,\,Kumar(2013)} /T_{Proposed Approach}$$

where, $T_{Dutta\,and\,\,Kumar(2013)}$ represents the trace value of a compromise solution obtained by Dutta and Kumar (2013) and $T_{Proposed Approach}$ represents the trace value of the compromise solution obtained by using the proposed approach (Table 15).

Table 15 Relative efficiency of solutions

From these results, it has been found that, due to the existence of conflicting objective function in the formulated MOLFIP, they cannot optimized sufficiently. In the same manner, the R.E. related to the first objective function decreases for the different levels of $\alpha$ and $\beta$, while the R.E. related to the second objective function increases for the different levels of $\alpha$ and $\beta$.

5 Managerial perceptions, contributions and limitations

5.1 Managerial perceptions

The following visions are drawn from the proposed work which is supportive of any operational managers in the manufacturing unit:

• The problem formulated in this paper is helpful to demonstrate a simulation study based on the realistic situation of inventory management, which is continuously faced by the operational managers in manufacturing and production unit, where DM want to optimize the different costs, which are directly related to the inventory management.

• The model considered holding cost, purchasing price, selling price, demand and ordering cost of the items with some ambiguity which is a natural phenomenon rather than an exact value, and hence, provides an elastic view to the operational managers to optimize the different inventory costs under ambiguity.

5.2 Contributions

The proposed work makes following contribution:

• A mathematical model for inventory management has been formulated with the primary objective to maximize the profit and minimize the holding cost of pre-ordered quantity.

• The proposed work gives the concept of intuitionistic fuzzy set theory in inventory management.

• Developed an FGP model for inventory management, where DM can control the quantity of ordered items.

• Different solution sets have been generated at some discrete values of $\alpha$ and $\beta$.

5.3 Limitations

There are some limitations related to our model which is given below:

• A hypothetical case study has been used to illustrate the proposed work.

• The proposed model limited to vagueness only, but in real-world problems decision maker has to face randomness and multi-choices situations.

• The role of deterioration during different production cycle is yet to be explored in this model.

• Fuzzy goal programming model is limited to linear membership function only. Hence, the role of other membership function in this model is yet to be explored.

6 Conclusion

In this paper, we have considered inventory modelling under IFS and maximize the profit and minimize the holding cost related to per-ordered quantity with some realistic set of constraints. The formulated problem cannot be solved unless it converted into an equivalent deterministic form, which has been done by using the ranking function approach by defining the membership and non-membership function respectively, which gives decision maker an optimistic and pessimistic view in multi-criterion decision making. The formulated models have been solved by using an FGP technique for attaining the most acceptable solution of the models by controlling the decision vectors at different levels of $\alpha$ and $\beta$. Tables 7 and 13 gives an optimum compromise solution with an optimum ordered quantity and in Table 14, the relative efficiency of the obtained solution has been compared with the deterministic model of inventory management. The procedure given in this manuscript can also be used for solving all those problems where the input information is in the form of an intuitionistic parameter. Such problems may be related to transportation problems, assignment problems, production planning problems, problems related to workforce management and many more. In a future study, the model can be further extended with different types of inventory and production-related costs and can also be solve with different types of linear and non-linear membership functions such exponential, hyperbolic, parabolic, piecewise linear, gaussian, and singleton membership function respectively.