Abstract
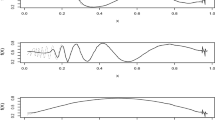
The problem of estimating the density-weighted average derivative of a regression function is considered. We present a new consistent estimator based on a plug-in approach and wavelet projections. Its performances are explored under various dependence structures on the observations: the independent case, the ρ-mixing case and the α-mixing case. More precisely, denoting n the number of observations, in the independent case, we prove that it attains 1/n under the mean squared error, in the ρ-mixing case, \(1/\sqrt{n}\) under the mean absolute error, and, in the α-mixing case, \(\sqrt{\ln n /n}\) under the mean absolute error. A short simulation study illustrates the theory.
Similar content being viewed by others
References
Antoniadis, A. (1997). Wavelets in statistics: a review (with discussion). J. Ital. Statist. Soc., 6, 97–144.
Banerjee, A.N. (2007). A method of estimating the average derivative. J. Econometrics, 136, 65–88.
Cattaneo, M.D., Crump, R.K. and Jansson, M. (2010). Robust data-driven inference for density-weighted average derivatives. J. Amer. Stat. Assoc., 105, 1070– 1083.
Cattaneo, M.D., Crump, R.K. and Jansson, M. (2008). Small bandwidth asymptotics for density-weighted average derivatives. CREATES Research Paper 200824. Available at SSRN: http://ssrn.com/abstract=1148173.
Carrasco, M. and Chen, X. (2002). Mixing and moment properties of various GARCH and stochastic volatility models. Econometric Theory, 18, 17–39.
Chaubey, Y.P. and Doosti, H. (2005). Wavelet based estimation of the derivatives of a density for m-dependent random variables. J. Iran. Stat. Soc., 4, 97–105.
Chaubey, Y.P., Doosti, H. and Prakasa Rao, B.L.S. (2006). Wavelet based estimation of the derivatives of a density with associated variables. Int. J. Pure Appl. Math., 27, 97–106.
Cohen, A., Daubechies, I., Jawerth, B. and Vial, P. (1993). Wavelets on the interval and fast wavelet transforms. Appl. Comput. Harmon. Anal., 24, 54–81.
Coppejans, M. and Sieg, H. (2005). Kernel Estimation of Average Derivatives and Differences. J. Bus. Econ. Stat., 23, 211–225.
Daubechies, I. (1992). Ten Lectures on Wavelets. CBMS-NSF regional conferences series in applied mathematics. SIAM, Philadelphia.
Davydov, Y. (1970). The invariance principle for stationary processes. Theor. Probab. Appl., 15, 498–509.
Deaton, A. and Ng, S. (1998). Parametric and nonparametric approaches to price and tax reform. J. Amer. Stat. Assoc., 93, 900–909.
Doukhan, P. (1994). Mixing. Properties and Examples. Lecture Notes in Statistics 85. Springer Verlag, New York.
Fryzlewicz, P. and Subba Rao, S. (2011). Mixing properties of ARCH and time-varying ARCH processes. Bernoulli, 17, 320–346.
Härdle, W. and Stoker, T.M. (1989). Investigating smooth multiple regression by the method of average derivatives. J. Amer. Stat. Assoc., 84, 986–995.
Härdle, W., Hildenbrand, W. and Jerison, M. (1991). Empirical evidence on the law of demand. Econometrica, 59, 1525–1549.
Härdle, W., Hart, J., Marron, J.S. and Tsybakov, A.B. (1992). Bandwidth choice for average derivative estimation. J. Amer. Stat. Assoc., 87, 417, 218–226.
Härdle, W. and Tsybakov, A.B. (1993). How sensitive are average derivatives?. J. Econom., 58, 31–48.
Härdle, W., Kerkyacharian, G., Picard, D. and Tsybakov, A. (1998). Wavelet, Approximation and Statistical Applications. Lectures Notes in Statistics 129. Springer Verlag, New York.
Hansen, B. (2009). Lecture Notes on Nonparametrics, Lecture Notes.
Juditsky, A. and Lambert-Lacroix, S. (2004). On minimax density estimation on R. Bernoulli, 10, 187–220.
Kolmogorov, A.N. and Rozanov, Yu.A. (1960). On strong mixing conditions for stationary Gaussian processes. Theor. Probab. Appl., 5, 204–208.
Lütkepohl, H. (1992). Multiple Time Series Analysis. Springer-Verlag, Heidelberg.
Mallat, S. (2009). A Wavelet Tour of Signal Processing, Third Edition. The Sparse Way, with Contributions from Gabriel Peyré. Elsevier/Academic Press, Amsterdam.
Marron, J.S., Adak, S., Johnstone, I.M., Neumann, M.H. and Patil, P. (1998). Exact risk analysis of wavelet regression. J. Comput. Graph. Statist., 7, 278–309.
Matzkin, R.L. (2007). Nonparametric Identification. In Handbook of Econometrics (J. Heckman and E. Leamer Eds.). Elsevier Science B.V., VIB, pp. 5307– 5368.
Meyer, Y. (1992). Wavelets and Operators. Cambridge University Press, Cambridge.
Powell, J.L., Stock, J.H. and Stoker, T.M. (1989). Semiparametric estimation of index coefficients. Econometrica, 57, 1403–1430.
Powell, J.L. (1994). Estimation of Semiparametric Models. In Handbook of Econometrics (R. Engle and D. McFadden Eds.). Elsevier Science B.V., IV, pp. 2443– 2521.
Powell, J.L. and Stoker, T.M. (1996). Optimal bandwidth choice for density-weighted averages. J. Econometrics, 75, 291–316.
Prakasa Rao, B.L.S. (1995). Consistent estimation of density-weighted average derivative by orthogonal series method. Statist. Probab. Lett., 22, 205–212.
Prakasa Rao, B.L.S. (1996). Nonparametric estimation of the derivatives of a density by the method of wavelets. Bull. Inform. Cybernet., 28, 91–10.
Reynaud-Bouret, P., Rivoirard, V. and Tuleau-Malot, C. (2011). Adaptive density estimation: a curse of support? J. Statist. Plann. Inference, 141, 115–139.
Rosenblatt, M. (1956). A central limit theorem and a strong mixing condition. Proc. Nat. Acad. Sci. USA, 42, 43–47.
Rosenthal, H.P. (1970). On the subspaces of \(\mathbb{L}_p\) (p ≥ 2) spanned by sequences of independent random variables. Israel J. Math., 8, 273–303.
Schafgans, M. and Zinde-Walsh, V. (2010). Smoothness adaptive average derivative estimation. Econom. J., 13, 40–62.
Shao, Q.-M. (1995). Maximal inequality for partial sums of ρ-mixing sequences. Ann. Probab., 23, 948–965.
Stoker, T.M. (1986). Consistent estimation of scaled coefficients. Econometrica, 54, 1461–1481.
Stoker, T.M. (1989). Tests of additive derivative constraints. Rev. Econ. Stud., 56, 535–552.
Stoker, T.M. (1991). Equivalence of Direct, Indirect and Slope Estimators of Average Derivatives, Nonparametric and Semiparametric Methods in Econometrics and Statistics (W.A. Barnett, J. Powell and G. Tauchen Eds.). Cambridge University Press.
Türlach, B.A. (1994). Fast implementation of density-weighted average derivative estimation. Computationally Intensive Statistical Methods, 26, 28–33.
White, H. and Domowitz, I. (1984). Nonlinear regression with dependent observations. Econometrica, 52, 143–162.
Vidakovic, B. (1999). Statistical Modeling by Wavelets. John Wiley & Sons, Inc., New York, 384 pp.
Zhengyan, L. and Lu, C. (1996). Limit Theory for Mixing Dependent Random Variables. Kluwer, Dordrecht.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Chesneau, C., Kachour, M. & Navarro, F. On the estimation of density-weighted average derivative by wavelet methods under various dependence structures. Sankhya A 76, 48–76 (2014). https://doi.org/10.1007/s13171-013-0032-1
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13171-013-0032-1
Keywords and phrases.
- Nonparametric estimation of density-weighted average derivative
- ‘plug-in’ approach, wavelets
- consistency
- ρ-mixing
- α-mixing