Skip to main content
SpringerLink
Log in

Extremal disc packings in compact hyperbolic surfaces

  • Published:
Revista Matemática Complutense Aims and scope Submit manuscript

Abstract

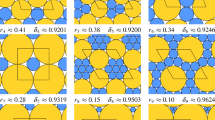
We study packings of metric discs with respect to the canonical hyperbolic metric of a compact Riemann surface of genus greater than one. We find the maximum radius of a packing as a function of the genus and the number of discs and we investigate some properties of the surfaces that contain an extremal packing.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Bavard, C.: Disques extrémaux et surfaces modulaires. Ann. Fac. Sci. Toulouse Math. (6) 5(2), 191–202 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bavard, C., Böröczky, K.J., Farkas, B., Prok, I., Vena, L., Wintsche, G.: Equality in László Fejes Tóth’s triangle bound for hyperbolic surfaces. Acta Sci. Math. (Szeged) 77(3–4), 669–679 (2011)

    MathSciNet  MATH  Google Scholar 

  3. Beardon, A.F.: The Geometry of Discrete Groups, Graduate Texts in Mathematics, vol. 91. Springer, New York (1983)

    Book  Google Scholar 

  4. Böröczky, K.: Packing of spheres in spaces of constant curvature. Acta Math. Acad. Sci. Hungar. 32(3–4), 243–261 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  5. Edmonds, A.L., Ewing, J.H., Kulkarni, R.S.: Torsion free subgroups of Fuchsian groups and tessellations of surfaces. Invent. Math. 69(3), 331–346 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  6. Girondo, E., González-Diez, G.: On extremal discs inside compact hyperbolic surfaces. C. R. Acad. Sci. Paris Sér. I Math. 329(1), 57–60 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  7. Girondo, E., González-Diez, G.: Genus two extremal surfaces: extremal discs, isometries and Weierstrass points. Isr. J. Math. 132, 221–238 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  8. Girondo, E., González-Diez, G.: On extremal Riemann surfaces and their uniformizing Fuchsian groups. Glasg. Math. J. 44(1), 149–157 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  9. Girondo, E., González-Diez, G.: Introduction to Compact Riemann Surfaces and dessins d’enfants. London Mathematical Society Student Texts, vol. 79. Cambridge University Press, Cambridge (2012)

    MATH  Google Scholar 

  10. Girondo, E., Nakamura, G.: Compact non-orientable hyperbolic surfaces with an extremal metric disc. Conform. Geom. Dyn. 11, 29–43 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  11. Girondo, E., Torres-Teigell, D., Wolfart, J.: Shimura curves with many uniform dessins. Math. Z. 271(3–4), 757–779 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  12. Jones, G.A., Wolfart, J.: Dessins D’enfants on Riemann Surfaces. Springer Monographs in Mathematics. Springer, Cham (2016)

    Book  MATH  Google Scholar 

  13. Maclachlan, C., Rosenberger, G.: Commensurability classes of two-generator Fuchsian groups. Discrete Groups and Geometry (Birmingham. 1991), London Mathematical Society Lecture Note Series, vol. 173, pp. 171–189. Cambridge University Press, Cambridge (1992)

    Chapter  Google Scholar 

  14. Nakamura, G.: Extremal disks and extremal surfaces of genus three. Kodai Math. J. 28(1), 111–130 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  15. Nakamura, G.: Compact non-orientable surfaces of genus 4 with extremal metric discs. Conform. Geom. Dyn. 13, 124–135 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  16. Nakamura, G.: Compact non-orientable surfaces of genus 5 with extremal metric discs. Glasg. Math. J. 54(2), 273–281 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  17. Nakamura, G.: Compact Klein surfaces of genus 5 with a unique extremal disc. Conform. Geom. Dyn. 17, 39–46 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  18. Takeuchi, K.: Arithmetic triangle groups. J. Math. Soc. Japan 29(1), 91–106 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  19. Takeuchi, K.: Commensurability classes of arithmetic triangle groups. J. Fac. Sci. Univ. Tokyo Sect. IA Math 24(1), 201–212 (1977)

    MathSciNet  MATH  Google Scholar 

  20. Wolfart, J.: The ‘obvious’ part of Belyi’s theorem and Riemann surfaces with many automorphisms. In: Geometric Galois Actions, 1, London Mathematical Society Lecture Note Series, vol. 242, pp. 97–112. Cambridge University Press, Cambridge (1997)

Download references

Acknowledgements

I am indebted to K. Böröczky and M. Conder for several valuable comments during the preparation of the article. Also to the reviewers for many interesting comments and questions that clearly improved the first version of the text.

Author information

Authors and Affiliations

  1. Departamento de Matemáticas, Universidad Autónoma de Madrid, Campus de Cantoblanco, 28049, Madrid, Spain

    Ernesto Girondo

  2. Instituto de Ciencias Matemáticas ICMAT, Nicolás Cabrera 13-15, Campus de Cantoblanco, 28049, Madrid, Spain

    Ernesto Girondo

Authors
  1. Ernesto Girondo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ernesto Girondo.

Additional information

This work was partially supported by the Grants MTM2012-31973 and MTM2016-79497-P of the Spanish MEyC and ICMAT Severo Ochoa project SEV-2015-0554 (MINECO).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Girondo, E. Extremal disc packings in compact hyperbolic surfaces. Rev Mat Complut 31, 467–478 (2018). https://doi.org/10.1007/s13163-017-0252-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13163-017-0252-3

Keywords

Mathematics Subject Classification

Search

Navigation