An optimal investment, consumption-leisure and voluntary retirement choice problem with subsistence consumption constraints

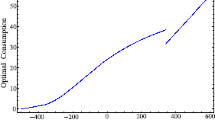
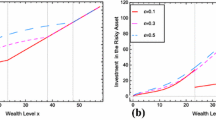
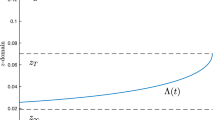
Abstract

We study an optimal investment, consumption-leisure and voluntary retirement problem for an agent whose consumption rate process is subject to a subsistence constraint before retirement. We use the dynamic programming method to obtain closed-form solutions for the optimal strategies as well as the value function when the agent’s utility of consumption and leisure is of Cobb–Douglas form.

Appendices

Appendix 1: Proof of the assertion that $C_2>0$ in (18) and $X'(c)>0$ for given X(c) in (22).

With the continuity condition of the value function V(x) at $\bar{x}$ (32), we obtain an alternative expression of $D_2$ as follows:

$$\begin{aligned} D_2=\frac{\rho }{r-\frac{1}{2}\theta ^2n_2}\Biggl (1-L^{\frac{\gamma -\gamma _1}{\gamma _1}}\Biggr )\frac{K_2^{\gamma _1 n_2}}{1-\gamma _1}\bar{x}^{\gamma _1 n_2+1}-\frac{r-\frac{1}{2}\theta ^2n_1}{r-\frac{1}{2}\theta ^2n_2}D_1(K_2\bar{x})^{\gamma _1(n_2-n_1)}. \end{aligned}$$

Since $0<\bar{x}_E<\bar{x}$, we have

$$\begin{aligned} \frac{r-\frac{1}{2}\theta ^2n_2-\frac{\rho }{1-\gamma _1}}{\frac{1}{2}\theta ^2\gamma _1 n_1 (n_2-n_1)}\left( \frac{1}{K_2}-\frac{1}{K_1}\right) =D_1(K_2\bar{x}_E)^{-(\gamma _1n_1+1)}>D_1(K_2\bar{x})^{-(\gamma _1n_1+1)}. \end{aligned}$$

(40)

Obviously, $\gamma _1n_1>-1$ and $-\gamma _1(n_2-n_1)>-(\gamma _1n_2+1),$ which is equivalent to the inequality

$$\begin{aligned} \frac{1}{2}\theta ^2\gamma _1\left( -\frac{2\rho }{\theta ^2}\right) (n_2-n_1)>-(\gamma _1n_2+1)\rho . \end{aligned}$$

From (33) and (34), $\displaystyle {-\frac{2\rho }{\theta ^2}}=(n_1+1)(n_2+1).$ So we have

$$\begin{aligned} \frac{1}{2}\theta ^2\gamma _1(n_1+1)(n_2+1)(n_2-n_1)>-(\gamma _1n_2+1)\rho , \end{aligned}$$

and

$$\begin{aligned} \frac{1}{2}\theta ^2\gamma _1(n_1+1)(n_2-n_1)<-\frac{(\gamma _1n_2+1)}{(n_2+1)}\rho = \left( r-\frac{1}{2}\theta ^2n_2-\frac{\rho }{1-\gamma _1}\right) (1-\gamma _1), \end{aligned}$$

where the relation $\displaystyle {\frac{r-\frac{1}{2}\theta ^2 n_{1, 2}}{\rho }}=\frac{n_{1, 2}}{n_{1, 2}+1}$ is used to obtain the above equality. Note that $K_1<K_2$ for $\gamma _1>1$ and $K_1>K_2$ for $0<\gamma _1<1$ from Remark 1. Consequently,

$$\begin{aligned} \frac{n_1+1}{(1-\gamma _1)n_1}\left( \frac{1}{K_2}-\frac{1}{K_1}\right) >\frac{r-\frac{1}{2}\theta ^2n_2-\frac{\rho }{1-\gamma _1}}{\frac{1}{2}\theta ^2\gamma _1 n_1 (n_2-n_1)}\left( \frac{1}{K_2}-\frac{1}{K_1}\right) . \end{aligned}$$

(41)

From (40) and (41), we derive

$$\begin{aligned} \frac{1}{(1-\gamma _1)}\left( \frac{1}{K_2}-\frac{1}{K_1}\right) >\frac{n_1}{n_1+1}D_1(K_2\bar{x})^{-(\gamma _1n_1+1)}=\frac{r-\frac{1}{2}\theta ^2 n_1}{\rho }D_1(K_2\bar{x})^{-(\gamma _1n_1+1)}, \end{aligned}$$

and

$$\begin{aligned} \rho \left( 1-L^{\frac{\gamma -\gamma _1}{\gamma _1}}\right) \frac{\bar{x}}{1-\gamma _1} -\left( r-\frac{1}{2}\theta ^2 n_1\right) D_1(K_2\bar{x})^{-\gamma _1n_1}>0, \end{aligned}$$

which yields that $D_2>0.$ From (26), we see that

$$\begin{aligned} X'(R)&=-\gamma _1 n_1 D_1 R^{-\gamma _1 n_1-1}-\gamma _1 n_2 D_2 R^{-\gamma _1 n_2-1}+\frac{1}{K_1}\\&={\frac{\frac{\gamma _1 n_1}{r}-\frac{\gamma _1 n_1}{K_1}-\frac{1}{K_1}}{(m_2-1)n_1-1}}-\gamma _1 n_2 D_2 R^{-\gamma _1 n_2-1}>0, \end{aligned}$$

which implies

$$\begin{aligned} \frac{\gamma _1 n_1}{r}-\frac{\gamma _1 n_1}{K_1}-\frac{1}{K_1}=-\frac{\frac{1}{2}\theta ^2n_1^2+\frac{1}{2\gamma _1}n_1\theta ^2}{rK_1}<0. \end{aligned}$$

Therefore we have $\widetilde{x}>(R-\epsilon )/r$ from the first equality of (29) and $C_2>0$ by (17). And, for $c\ge R$,

$$\begin{aligned} X'(c)&=-\gamma _1 n_1 D_1 c^{-\gamma _1 n_1 -1}-\gamma _1 n_2 D_2 c^{-\gamma _1 n_2 -1}+\frac{1}{K_1}\\&\ge -\gamma _1 n_1D_1R^{-\gamma _1 n_1 -1}+\frac{1}{K_1}-\gamma _1 n_2 D_2 c^{-\gamma _1 n_2 -1}\\&=\displaystyle {\frac{\frac{\gamma _1 n_1}{r}-\frac{\gamma _1 n_1}{K_1}-\frac{1}{K_1}}{(m_2-1)n_1-1}}-\gamma _1 n_2 D_2 c^{-\gamma _1 n_2 -1}>0. \end{aligned}$$

$\square$

Appendix 2: An extension: pre- and post-retirement subsistence consumption

We consider the situation where there exists a post-retirement subsistence consumption $\hat{R}$ as well as a pre-retirement subsistence consumption R. The value function of the retiree is then given by

$$\begin{aligned} \varPhi ^{p}(x)\triangleq \max _{(\mathbf{c},{\varvec{\pi }})\in \mathcal {\hat{A}}(x)}\mathbb {E} \left[ L^{\gamma _1-\gamma }\int _0^\infty e^{-\rho t}\frac{c_t^{1-\gamma _1}}{1-\gamma _1}dt\right] , \end{aligned}$$

subject to

$$\begin{aligned} dX_t=\left[ rX_t+\pi _t(\mu -r)-c_t\right] dt+\pi _t \sigma dB_t, \end{aligned}$$

where $\mathcal {\hat{A}}(x)$ is an admissible set (at initial wealth $X_0=x>\hat{R}/\epsilon$), which consists of pairs of consumption/portfolio $(\mathbf{c},{\varvec{\pi }})$ such that $X_t>\hat{R}/\epsilon$ and $c_t\ge \hat{R}$ for all $t\ge 0$. Along similar lines to the proof of Theorem 2 (or see Shim et al. [19]), we obtain

$$\begin{aligned} \varPhi ^{p}(x)/L^{\gamma _1-\gamma }=\left\{ \begin{array}{ll} a\left( x-\frac{\hat{R}}{r}\right) ^{m_2}+\frac{\hat{R}^{1-\gamma _1}}{\rho (1-\gamma _1)},&{}\quad ~\text{ for }~~\hat{R}/r< x<\hat{x} ,\\ \frac{r-\frac{1}{2}\theta ^2 n_1}{\rho } b \zeta ^{-\gamma _1(n_1+1)}+\frac{\zeta ^{1-\gamma _1}}{K_1(1-\gamma _1)},&{}\quad ~\text{ for }~~ x\ge \hat{x}, \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} b=\frac{\left( \frac{m_2-1}{\gamma _1}+1\right) \frac{1}{K_1}-\frac{1}{r}}{(m_2-1)n_1-1}\hat{R}^{\gamma _1 n_1 +1},~\hat{x}=b \hat{R}^{-\gamma _1 n_1}+\frac{\hat{R}}{K_1} \end{aligned}$$

and

$$\begin{aligned} a=\frac{1}{m_2}\left( \hat{x}-\frac{\hat{R}}{r}\right) ^{1-m_2} \hat{R}^{-\gamma _1}. \end{aligned}$$

$\hat{x}$ is the threshold wealth level corresponding to the subsistence consumption $\hat{R}$. For $x\ge \hat{x}$, $\zeta$ is determined from the following algebraic equation

$$\begin{aligned} x=b \zeta ^{-\gamma _1 n_1}+\frac{\zeta }{K_1}, \end{aligned}$$

(42)

which is the relationship between the optimal consumption rate $\zeta$ and the wealth level x. The optimal consumption and portfolio pair $(\mathbf{c}^{p,*},{\varvec{\pi }}^{p,*})$ for the retiree is given by

$$\begin{aligned} c_t^{p,*}=\left\{ \begin{array}{ll} \hat{R},&{}\quad ~\text{ for }~~\hat{R}/r< X_t<\hat{x}\\ \zeta _t,&{}\quad ~\text{ for }~~X_t\ge \hat{x} \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \pi _t^{p,*}=\left\{ \begin{array}{ll} \frac{\theta }{\sigma }\frac{1}{1-m_2}\left( X_t-\frac{\hat{R}}{r}\right) ,&{}\quad ~\text{ for }~~\hat{R}/r< X_t<\hat{x}\\ \frac{\theta }{\sigma \gamma _1}\left( -\gamma _1 n_1 b \zeta _t^{-\gamma _1 n_1}+\frac{\zeta _t}{K_1} \right) ,&{}\quad ~\text{ for }~~ X_t\ge \hat{x}, \end{array}\right. \end{aligned}$$

where $\zeta _t$ is determined by the following algebraic equation

$$\begin{aligned} X_t=b \zeta _t^{-\gamma _1 n_1}+\frac{\zeta _t}{K_1}. \end{aligned}$$

(43)

Then the agent’s optimization problem can the be written as

$$\begin{aligned} \varPhi (x)\triangleq \max _{(\mathbf{c},{\varvec{\pi }}, \tau )\in {\mathcal {A}}(x)}{\mathbb {E}} \left[ \int _0^\tau e^{-\rho t}\frac{c_t^{1-\gamma _1}}{1-\gamma _1}dt+e^{-\rho \tau }\varPhi ^{p}(X_\tau )\right] , \end{aligned}$$

and the value function $\varPhi (x)$ can be pursued by similar lines to the proof of Theorem 2.

Theorem 4

$$\begin{aligned} \varPhi (x)=\left\{ \begin{array}{ll} \displaystyle {c_2\left( x-\frac{R}{r}+\frac{\epsilon }{r}\right) ^{m_2}+\frac{R^{1-\gamma _1}}{\rho (1-\gamma _1)}},&{}\quad \text{ for }~~(R-\epsilon )/r< x<\check{x} ,\\ \displaystyle {\frac{r-\frac{1}{2}\theta ^2 n_1}{\rho } d_1 \eta ^{-\gamma _1(n_1+1)}}&{}\\ \quad \displaystyle {+\frac{r-\frac{1}{2}\theta ^2 n_2}{\rho } d_2 \eta ^{-\gamma _1(n_2+1)}+ \frac{\eta ^{1-\gamma _1}}{K_1(1-\gamma _1)}},&{}\quad \text{ for }~~\check{x}\le x<\bar{\check{x}} , \\ \varPhi ^{p}(x),&{}\quad \text{ for }~~\bar{\check{x}}\le x , \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} c_2&=C_2,~d_1=D_1,~\\ d_2&=-(d_1-L^{-n_1(\gamma _1-\gamma )}b)\bar{c}_l^{\gamma _1(n_2-n_1)}+\left( \frac{1}{K_2}-\frac{1}{K_1}\right) \bar{c}_l^{\gamma _1 n_2+1}+\frac{\epsilon }{r}\bar{c}_l^{\gamma _1 n_2}, \end{aligned}$$

and $\bar{c}_l$ solves the following algebraic equation

$$\begin{aligned}&\frac{1}{2}\theta ^2(n_2-n_1)(d_1-L^{-n_1(\gamma _1-\gamma )}b)\bar{c}_l^{-\gamma _1 n_1}\!+\!\left( r-\frac{1}{2}\theta ^2n_2-\frac{\rho }{1-\gamma _1}\right) \left( \frac{1}{K_2}-\frac{1}{K_1}\right) \bar{c}_l\nonumber \\&\quad +\left( r-\frac{1}{2}\theta ^2n_2\right) \frac{\epsilon }{r}=0. \end{aligned}$$

(44)

Furthermore,

$$\begin{aligned} \check{x}=d_1 R^{-\gamma _1 n_1}+d_2 R^{-\gamma _1 n_2}+\frac{R}{K_1}-\frac{\epsilon }{r},~~ \bar{\check{x}}=d_1 \bar{c}_l^{-\gamma _1 n_1}+d_2 \bar{c}_l^{-\gamma _1 n_2}+\frac{\bar{c}_l}{K_1}-\frac{\epsilon }{r}. \end{aligned}$$

$\check{x}$ is the threshold wealth level corresponding to the subsistence consumption R and $\bar{\check{x}}$ is the retirement wealth level. For $\check{x}\le x<\bar{\check{x}}$, $\eta$ is determined from the following algebraic equation

$$\begin{aligned} x=d_1 \eta ^{-\gamma _1 n_1}+d_2 \eta ^{-\gamma _1 n_2}+\frac{\eta }{K_1}-\frac{\epsilon }{r}, \end{aligned}$$

which is the relationship between the optimal consumption rate $\eta$ and the wealth level x.

Proof

Similar arguments to the proof of Theorem 2 lead us to have

$$\begin{aligned} \varPhi (x)=\displaystyle {c_2\left( x-\frac{R}{r}+\frac{\epsilon }{r}\right) ^{m_2}+\frac{R^{1-\gamma _1}}{\rho (1-\gamma _1)}},\quad \text{ for }~~(R-\epsilon )/r< x<\check{x}, \end{aligned}$$

and

$$\begin{aligned} \varPhi (x)= & {} \displaystyle {\frac{r-\frac{1}{2}\theta ^2 n_1}{\rho } d_1 \eta ^{-\gamma _1(n_1+1)}+\frac{r-\frac{1}{2}\theta ^2 n_2}{\rho } d_2 \eta ^{-\gamma _1(n_2+1)}+ \frac{\eta ^{1-\gamma _1}}{K_1(1-\gamma _1)}},~\\ \text{ for }~~\check{x}\le & {} x<\bar{\check{x}}, \end{aligned}$$

where

$$\begin{aligned} x=d_1 \eta ^{-\gamma _1 n_1}+d_2 \eta ^{-\gamma _1 n_2}+\frac{\eta }{K_1}-\frac{\epsilon }{r}, \end{aligned}$$

(45)

for some constants $c_2$, $d_1$, and $d_2.$ Boundary conditions at $x=\check{x}$ yield $c_2=C_2$, $d_1=D_1$, and $\check{x}=d_1 R^{-\gamma _1 n_1}+d_2 R^{-\gamma _1 n_2}+\frac{R}{K_1}-\frac{\epsilon }{r}.$

To determine $d_2$ and $\bar{\check{x}}$, we use the smooth-pasting condition at $x=\bar{\check{x}}$. Let us denote $\check{\tau }^*\triangleq \inf \{t\ge 0: X_t\ge \bar{\check{x}}\}$,  $\bar{c}_l\triangleq c_{\check{\tau }^*-}$, $\bar{c}_r\triangleq c_{\check{\tau }^*}$. From (42) and (45), we have

$$\begin{aligned} \bar{\check{x}}=d_1 \bar{c}_l^{-\gamma _1 n_1}+d_2 \bar{c}_l^{-\gamma _1 n_2}+\frac{\bar{c}_l}{K_1}-\frac{\epsilon }{r}=b \bar{c}_r^{-\gamma _1 n_1}+\frac{\bar{c}_r}{K_1}, \end{aligned}$$

(46)

the continuity of $\varPhi (x)$ at $x=\bar{\check{x}}$ yields

$$\begin{aligned} \varPhi (\bar{\check{x}})&=\displaystyle {\frac{r-\frac{1}{2}\theta ^2 n_1}{\rho } d_1 \bar{c}_l^{-\gamma _1(n_1+1)}+\frac{r-\frac{1}{2}\theta ^2 n_2}{\rho } d_2 \bar{c}_l^{-\gamma _1(n_2+1)}+\frac{\bar{c}_l^{1-\gamma _1}}{K_1(1-\gamma _1)}}\nonumber \\&=L^{\gamma _1-\gamma }\frac{r-\frac{1}{2}\theta ^2 n_1}{\rho } b \bar{c}_r^{-\gamma _1(n_1+1)}+L^{\gamma _1-\gamma }\frac{\bar{c}_r^{1-\gamma _1}}{K_1(1-\gamma _1)}, \end{aligned}$$

(47)

and the continuity of $\varPhi '(x)$ at $x=\bar{\check{x}}$ does

$$\begin{aligned} \varPhi '(\bar{\check{x}})=\bar{c}_l^{-\gamma _1}=L^{\gamma _1-\gamma }\bar{c}_r^{-\gamma _1}. \end{aligned}$$

(48)

It follows from the Eqs. (46), (47), and (48) that $\bar{c}_l$ solves the algebraic equation

$$\begin{aligned}&\frac{1}{2}\theta ^2(n_2-n_1)(d_1-L^{-n_1(\gamma _1-\gamma )}b)\bar{c}_l^{-\gamma _1 n_1}\!+\!\left( r-\frac{1}{2}\theta ^2n_2-\frac{\rho }{1-\gamma _1}\right) \left( \frac{1}{K_2}-\frac{1}{K_1}\right) \bar{c}_l\\&\quad +\left( r-\frac{1}{2}\theta ^2n_2\right) \frac{\epsilon }{r}=0, \end{aligned}$$

and $d_2$ can be found from (46). $\Box$

The following optimal strategies are immediate consequences of the first order conditions (FOCs).

Theorem 5

The optimal strategies $(\mathbf{c}^*,{\varvec{\pi }}^*, \tau ^*)$ for the agent are given by

$$\begin{aligned} c_t^{*}= & {} \left\{ \begin{array}{ll} R,~&{}\quad \text{ for }~~(R-\epsilon )/r< X_t<\check{x} ,\\ \eta _t,~&{}\quad \text{ for }~~\check{x}\le X_t<\bar{\check{x}} , \\ \zeta _t,~&{}\quad \text{ for }~~\bar{\check{x}}\le X_t , \end{array} \right. \\ \pi _t^{*}= & {} \left\{ \begin{array}{ll} \displaystyle {\frac{\theta }{\sigma }\cdot \frac{1}{1-m_2}\left( X_t-\frac{R}{r}+\frac{\epsilon }{r}\right) },~&{}\quad \text{ for }~~(R-\epsilon )/r< X_t<\check{x} ,\\ \displaystyle {\frac{\theta }{\sigma }\left( -n_1d_1\eta _t^{-\gamma _1 n_1}-n_2d_2\eta _t^{-\gamma _1 n_2}+\frac{\eta _t}{\gamma _1 K_1}\right) },~&{}\quad \text{ for }~~\check{x}\le X_t<\bar{\check{x}} , \\ \frac{\theta }{\sigma \gamma _1}\left( -\gamma _1 n_1 b \zeta _t^{-\gamma _1 n_1}+\frac{\zeta _t}{K_1} \right) ,~&{}\quad \text{ for }~~\bar{\check{x}}\le X_t , \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \tau ^*=\inf \{t\ge 0: X_t\ge \bar{\check{x}}\}, \end{aligned}$$

where $\eta _t$ and $\zeta _t$ solves the following algebraic equations

$$\begin{aligned} X_t=d_1 \eta _t^{-\gamma _1 n_1}+d_2 \eta _t^{-\gamma _1 n_2}+ \frac{\xi _t}{K_1}-\frac{\epsilon }{r},~~X_t=b \zeta _t^{-\gamma _1 n_1}+\frac{\zeta _t}{K_1}, \end{aligned}$$

respectively.

Proposition 3

If $L^{n_1(\gamma _1-\gamma )}<\left( \frac{\hat{R}}{R}\right) ^{\gamma _1n_1+1},$ the algebraic equation (44) has a unique solution and $\bar{c}_l$ decreases with R, while increases with $\hat{R}$.

Proof

If we define a function H(x) as follows:

$$\begin{aligned} H(x)\triangleq & {} \frac{1}{2}\theta ^2(n_2-n_1)(d_1-L^{-n_1(\gamma _1-\gamma )}b)\bar{c}_l^{-\gamma _1 n_1}\\&+\left( r-\frac{1}{2}\theta ^2n_2-\frac{\rho }{1-\gamma _1}\right) \left( \frac{1}{K_2}-\frac{1}{K_1}\right) \bar{c}_l\\&+\left( r-\frac{1}{2}\theta ^2n_2\right) \frac{\epsilon }{r}, \end{aligned}$$

we see that H(x) is a strictly decreasing function with $\displaystyle {\lim _{x \rightarrow 0}H(x)=+\infty }$ and $\displaystyle {\lim _{x \rightarrow \infty }H(x)=-\infty }$. So, $H(x)=0$ has a unique solution $\bar{c}_l>0.$ Taking partial derivatives of (44) with respect to R and $\hat{R}$ yields

$$\begin{aligned} \frac{\partial \bar{c}_l}{\partial R}<0\quad \text{ and }\quad \frac{\partial \bar{c}_l}{\partial \hat{R}}>0. \end{aligned}$$

$\square$

Remark 3

It can be easily shown that $\bar{\check{x}}$ increases with $\bar{c}_l$. From Proposition 3, if $L^{n_1(\gamma _1-\gamma )}<\left( \frac{\hat{R}}{R}\right) ^{\gamma _1n_1+1}$, it follows that $\bar{\check{x}}$ decreases with R, while increases with $\hat{R}$. In this case, pre-retirement subsistence consumption R stimulates early retirement but post-retirement subsistence consumption $\hat{R}$ delays retirement.