A new method of convergence acceleration of series expansion for analytic functions in the complex domain

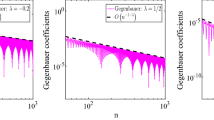
Abstract

This paper proposes a new method of convergence acceleration of series expansion of complex functions which are analytic on and inside the unit circle in the complex plane. This class of complex functions may have some singularities outside the unit circle, which dominate convergence of series expansion. In the proposed method, the singular points are moved away from the origin using conformal mapping, and the function is expanded using a sequence of polynomials orthogonalized on the boundary of the mapped complex domain. The decay rate of coefficients of the orthogonal polynomial expansion can be related to the convergence region in a similar form to the Cauchy–Hadamard formula for power series. Using this relation, we quantitatively evaluate and maximize the convergence rate of the improved series. Numerical examples demonstrate that the proposed method is effective for slow convergent series, and may converge faster than Padé approximants.

Appendix. The proof of the contraction property (14) of the map \(F\) in Theorem 1

The contraction property (14) of the map $F$ in Theorem 1 can be proved as follows. First, for convenience, we write (12) as $H_{\beta ^*}(\zeta ) = G_\mu (H_\beta (z))$ with $H_{\beta ^*} :\zeta \mapsto \hat{z}$, $H_\beta :z \mapsto \check{z}$ and $G_\mu :\check{z} \mapsto \hat{z}$ defined by

$$\begin{aligned} H_{\beta ^*}(\zeta ) = \frac{1 - \beta ^*\zeta }{1 + \beta ^*\zeta } , \quad H_\beta (z) = \frac{1 - \beta z}{1 + \beta z} \quad \text{ and } \quad G_{\mu }(\check{z}) = \check{z}^{\mu } . \end{aligned}$$

(45)

Then the map $F$ defined by (9) can be rewritten in the form

$$\begin{aligned} F = H_{\beta ^{*}}^{-1} \circ G_{\mu } \circ H_{\beta } , \end{aligned}$$

(46)

and the contraction property (14) can be expressed as

$$\begin{aligned} H_{\beta ^{*}}^{-1} (G_{\mu } (H_{\beta }(D_z))) \ \subset \ D_\zeta , \end{aligned}$$

(47)

where $D_z$ and $D_\zeta$ are the unit disks $|z| < 1$ in the $z$-plane and $|\zeta | < 1$ in the $\zeta$-plane, respectively. Thus we can prove (14) by showing that

$$\begin{aligned} G_{\mu }(H_{\beta }(D_z)) \ \subset \ H_{\beta ^{*}}(D_\zeta ) . \end{aligned}$$

(48)

Using $\hat{z} = r \mathrm {e}^{\mathrm {i}\theta }$, the boundary of $G_{\mu }(H_{\beta }(D_z))$ in the $\hat{z}$-plane is given by

$$\begin{aligned} r^{2/\mu } - \{ (B+B^{-1}) \cos (\theta /\mu ) \} r^{1/\mu } + 1 = 0 , \end{aligned}$$

(49)

where $B = (1 + \beta )/(1 - \beta ) > 1$. Similarly, noting that $(1+\beta ^{*})/(1-\beta ^{*}) = B^{\mu }$, we can represent the boundary of $H_{\beta ^{*}}(D_\zeta )$ by

$$\begin{aligned} r^{2} - \{ (B^{\mu }+B^{-\mu }) \cos \theta \} r + 1 = 0 . \end{aligned}$$

(50)

The domains $G_{\mu }(H_{\beta }(D_z))$ and $H_{\beta ^{*}}(D_\zeta )$ are both in the right half of the $\hat{z}$-plane and symmetric with respect to the real axis, as shown in Fig. 13. Thus it suffices to consider the region for $0 \le \theta < \pi /2$ in the $\hat{z}$-plane. Equations (49) and (50) are quadratic with respect to $r^{1/\mu }$ and $r$, respectively, and the corresponding discriminants for $r \ge 0$ and $0 \le \theta < \pi /2$ produce the following conditions:

Fig. 13

The mapped domains $G_{\mu }(H_{\beta }(D_z))$ and $H_{\beta ^{*}}(D_\zeta )$ in the $\hat{z} ~ (=\hat{x} + \mathrm {i}\hat{y})$-plane for $\beta = 0.9$ and $\mu = 0.4$. The solid and dashed closed curves represent the boundaries of $G_{\mu }(H_{\beta }(D_z))$ and $H_{\beta ^{*}}(D_\zeta )$, respectively. The maps $H_{\beta }$, $H_{\beta ^*}$ and $G_\mu$ are defined in (45). $D_z$ and $D_\zeta$ denote the the unit disks $|z| < 1$ in the $z$-plane and $|\zeta | < 1$ in the $\zeta$-plane, respectively. The straight lines $\mathrm {OP}$ and $\mathrm {OQ}$ are in contact with $G_{\mu }(H_{\beta }(D_z))$ at $\mathrm {P}$ and $H_{\beta ^{*}}(D_\zeta )$ at $\mathrm {Q}$, respectively. The points $\mathrm {P}_1$, $\mathrm {P}_2$, $\mathrm {Q}_1$ and $\mathrm {Q}_2$ are on the same straight line. $\theta _{\mathrm {P}} = \angle \,\mathrm {P}_0\mathrm {O}\mathrm {P}$, $\theta _{\mathrm {Q}} = \angle \,\mathrm {P}_0\mathrm {O}\mathrm {Q}$, $r_{\mathrm {P}_1} = \overline{\mathrm {OP}_1}$, $r_{\mathrm {P}_2} = \overline{\mathrm {OP}_2}$, $r_{\mathrm {Q}_1} = \overline{\mathrm {OQ}_1}$ and $r_{\mathrm {Q}_2} = \overline{\mathrm {OQ}_2}$

$$\begin{aligned} \sin (\theta /\mu ) \le \tanh \ell _B \quad \text{ and } \quad \sin \theta \le \tanh (\mu \, \ell _B) , \end{aligned}$$

(51)

where $\ell _B = \log B > 0$. For the cases of equality $\sin (\theta /\mu ) = \tanh \ell _B$ and $\sin \theta = \tanh (\mu \,\ell _B)$ in (51), we write $\theta = \theta _{\mathrm {P}}$ and $\theta = \theta _{\mathrm {Q}}$, respectively, namely

$$\begin{aligned} \theta _{\mathrm {P}} = \mu \, \mathrm {arcsin}(\tanh \ell _B) \quad \text{ and } \quad \theta _{\mathrm {Q}} = \mathrm {arcsin}(\tanh (\mu \,\ell _B)) . \end{aligned}$$

(52)

Also let $r_{\mathrm {P}_1}(\theta )$ and $r_{\mathrm {P}_2}(\theta )$ be the solutions of (49) with $r_{\mathrm {P}_1}(\theta ) \le r_{\mathrm {P}_2}(\theta )$ for $0\le \theta \le \theta _{\mathrm {P}}$, and let $r_{\mathrm {Q}_1}(\theta )$ and $r_{\mathrm {Q}_2}(\theta )$ be the solutions of (50) with $r_{\mathrm {Q}_1}(\theta ) \le r_{\mathrm {Q}_2}(\theta )$ for $0\le \theta \le \theta _{\mathrm {Q}}$, as shown in Fig. 13. We can show that $\theta _{\mathrm {Q}}/\theta _{\mathrm {P}}$ is the monotone decreasing function with respect to $\mu$, and that $\mathrm {d}\log r_{\mathrm {Q}_1}/\mathrm {d}\theta \le \mathrm {d}\log r_{\mathrm {P}_1}/\mathrm {d}\theta$ and $\mathrm {d}\log r_{\mathrm {P}_2}/\mathrm {d}\theta \le \mathrm {d}\log r_{\mathrm {Q}_2}/\mathrm {d}\theta$. From these, we get

$$\begin{aligned} \theta _{\mathrm {P}} \le \theta _{\mathrm {Q}} , \end{aligned}$$

(53)

and

$$\begin{aligned} r_{\mathrm {Q}_1}(\theta ) \le r_{\mathrm {P}_1}(\theta ) \le r_{\mathrm {P}_2}(\theta ) \le r_{\mathrm {Q}_2}(\theta ) \,\, \,\,\quad \text{ for } \ 0 \le \theta \le \theta _{\mathrm {P}} . \end{aligned}$$

(54)

These results indicate that (48) holds, and thus the contraction property (14) of the map $F$ in Theorem 1 is proved.