Abstract
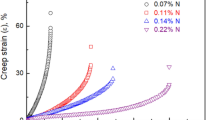
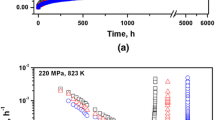
Effect of nitrogen on primary and steady state creep deformation behaviour of 316LN austenitic stainless steel has been studied. Nitrogen content was varied between 0.07 and 0.22 wt%. Creep tests have been carried out on the steels over the stress range of 120–225 MPa at 923 K. The creep behaviour of the steels has been assessed based on Garofalo relationship, \(\varepsilon = \varepsilon_{o} + \varepsilon_{T} \left[ {1 - exp\left( { - rt} \right)} \right] + \dot{\varepsilon }_{s} t\). The rate of exhaustion of primary creep rate ‘r’ and steady state creep rate ‘\(\dot{\varepsilon }_{s}\)’ decrease and time to onset the secondary creep stage increases with nitrogen content. The relationships between the initial creep rate ‘\(\dot{\varepsilon }_{i}\)’and rate of exhaustion of primary creep rate ‘r’ with steady creep rate ‘\(\dot{\varepsilon }_{s}\)’ reveal that the same deformation mechanism prevails during the transient and steady state creep deformations. Attempt has been made to generate a master transient creep curve for the steels having different nitrogen contents using the above parameters. Even though for a steel of specific nitrogen content, master curve has been generated for different stress levels, a master curve for all the steel could not be established. Different deformation characteristics of the steel having different nitrogen content which effect the stacking fault energy as well as precipitation behaviour is considered for the disagreement.















Similar content being viewed by others
Abbreviations
- ε:
-
Creep strain
- t:
-
Time
- εo :
-
Instantaneous strain on loading
- \(\varepsilon_{T }\) :
-
Transient creep strain
- \(r\) :
-
Rate of exhaustion of primary creep
- \(\dot{\varepsilon }_{s}\) :
-
Steady state creep rate
- \(\dot{\varepsilon }_{i}\) :
-
Initial creep rate
- τ:
-
Relaxation time for rearrangement of dislocations into stable configuration
- K:
-
Constant
- β:
-
Constant
- tos :
-
Time for onset of secondary
References
Simmons J W, Mat Sci Eng A207 (1996) 159.
Gavriljuk V G, and Berns H (eds) High Nitrogen Steels, Springer, Berlin (1999).
Speidel M O, in Proceedings of International Conference on High Nitrogen Steels HNS 88, France, May 1988, (eds) Foct J, and Hendry A, The Institute of Metals, London (1989), p 92.
Vanaja J, Laha K, and Mathew M D, Met Trans 45A (2014) 5076.
Sidey D, and Wilshire B, Met Sci J 3 (1969) 56.
Phaniraj C, Nandagopal M, Mannan S L, and Rodriguez P, Acta Metall Mater 39 (1991) 651.
Webster G A, Cox A P D, and Dorn J E Metal Sci J 3 (1969) 221.
Conway J B, Numerical Methods for Creep and Rupture Analysis, Gordon and Breach, New York (1968).
Scframm R E, and Reed R P, Met Trans 6A (1975) 1345.
High Nitrogen Steels, Structure, Properties, Manufacture, Applications, Valentin Gavriljuk, Hans Berns. Springer, Berlin (1999). doi:10.1007/978-3-662-03760-7.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Nandagopal, M., Ganesan, V. & Laha, K. Effect of Nitrogen on Primary and Steady State Creep Deformation Behaviour of 316LN Austenitic Stainless Steel. Trans Indian Inst Met 70, 783–790 (2017). https://doi.org/10.1007/s12666-017-1088-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12666-017-1088-8