Abstract
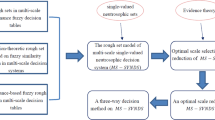
The paper discusses the trapezoidal fuzzy number (TrFN); interval-valued intuitionistic fuzzy number (IVIFN); neutrosophic set and its operational laws; and, trapezoidal neutrosophic set (TrNS) and its operational laws. Based on the combination of IVIFN and TrNS, an interval valued trapezoidal neutrosophic set (IVTrNS) is proposed followed by its operational laws. The paper also presents the score and accuracy functions for the proposed interval valued trapezoidal neutrosophic number (IVTrNN). Then, an interval valued trapezoidal neutrosophic weighted arithmetic averaging (IVTrNWAA) operator is introduced to combine the trapezoidal information which is neutrosophic and in the unit interval of real numbers. Finally, a method is developed to handle the problems in the multi attribute decision making (MADM) environment using IVTrNWAA operator followed by a numerical example of NFRs prioritization to illustrate the relevance of the developed method.


Similar content being viewed by others
References
Akram M, Ilyas F, Garg H (2019) Multi-criteria group decision making based on ELECTRE I method in Pythagorean fuzzy information. Soft Comput 24(5):3425–3453. https://doi.org/10.1007/s00500-019-04105-0
Anton A (1997) Goal identification and refinement in the specification of software-based information systems. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA
Ashraf S, Abdullah S, Mahmood T (2019) Spherical fuzzy Dombi aggregation operators and their application in group decision-making problems. J Ambient Intell Hum Comput. https://doi.org/10.1007/s12652-019-01333-y
Atanassov K (2017) Type-1 fuzzy sets and intuitionistic fuzzy sets. Algorithms 10(3):106. https://doi.org/10.3390/a10030106
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96. https://doi.org/10.1016/s0165-0114(86)80034-3
Atanassov KT (1999) Interval valued intuitionistic fuzzy sets. Intuitionistic Fuzzy Sets Stud Fuzziness Soft Comput. https://doi.org/10.1007/978-3-7908-1870-3_2
Atanassov KT (2000) Two theorems for intuitionistic fuzzy sets. Fuzzy Sets Syst 110(2):267–269. https://doi.org/10.1016/s0165-0114(99)00112-8
Atanassov K, Gargov G (1989) Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst 31(3):343–349. https://doi.org/10.1016/0165-0114(89)90205-4
Chen TY (2010) An outcome-oriented approach to multicriteria decision analysis with intuitionistic fuzzy optimistic/pessimistic operators. Expert Syst Appl 37(12):7762–7774. https://doi.org/10.1016/j.eswa.2010.04.064
Dey PP, Pramanik S, Giri BC (2016) TOPSIS for solving multi-attribute decision making problems under bi-polar neutrosophic environment. In: Smarandache F, Pramanik S (eds) New trends in neutrosophic theory and applications. Pons Editions, Brussels, pp 65–77
Dong JY, Wan SP (2015) Interval-valued trapezoidal intuitionistic fuzzy generalized aggregation operators and application to multi-attribute group decision making. Scientia Iranica 22(6):2702–2715
Glinz M (2007) On non-functional requirements. In: 15th IEEE International Requirements Engineering Conference, 21–26
Gong Z, Hai S (2014) The interval-valued trapezoidal approximation of interval-valued fuzzy numbers and its application in fuzzy risk analysis. J Appl Math 2014:1–22. https://doi.org/10.1155/2014/254853
Goguen J (1967) L-fuzzy sets. J Math Anal Appl 18:145–174
Jana C, Pal M, Wang J (2019) Bipolar fuzzy Dombi aggregation operators and its application in multiple-attribute decision-making process. J Ambient Intell Hum Comput 10:3533–3549. https://doi.org/10.1007/s12652-018-1076-9
Joshi R (2020) A new multi-criteria decision-making method based on intuitionistic fuzzy information and its application to fault detection in a machine. J Ambient Intell Hum Comput 11:739–753. https://doi.org/10.1007/s12652-019-01322-1
Joshi BP, Kumar S (2012) Fuzzy time series model based on intuitionistic fuzzy sets for empirical research in stock market. Int J Appl Evol Comput 3(4):71–84. https://doi.org/10.4018/jaec.2012100105
Khatter K, Kalia A (2012) Goal based analysis of non-functional requirements for webbased Systems. CSI J Comput 1(4):3–20 (ISSN: 2277–7091)
Khatter K, Kalia A (2013a) Impact of non-functional requirements on requirements evolution. Sixth international conference on emerging trends in engineering and technology-ICETET 2013, IEEE Computer Society 61–68. https://doi.org/10.1109/ICETET.2013.15
Khatter K, Kalia A (2013b) Integration of non-functional requirements in model-driven architecture. Fifth International conference on advances in recent technologies in communication and computing (ARTCom 2013). https://doi.org/10.1049/cp.2013.2213
Khatter K, Kalia A (2014) Quantification of non-functional requirements. Sixth international conference on contemporary computing-IC3 2014. 224–229, IEEE Computer Society, https://doi.org/10.1109/IC3.2014.6897177
Kumar R, Khatter K, Kalia A (2011) Measuring software reliability: a fuzzy model. SIGSOFT Softw Eng Notes 36:1–6
Li J, Zeng W, Guo P (2014) Interval-valued intuitionistic trapezoidal fuzzy number and its application. 2014 IEEE International Conference on Systems, Man, and Cybernetics (SMC). https://doi.org/10.1109/smc.2014.6973997
Liang Y, Qin J, Martínez L, Liu J (2020) A heterogeneous QUALIFLEX method with criteria interaction for multi-criteria group decision making. Inf Sci 512:1481–1502. https://doi.org/10.1016/j.ins.2019.10.044
Liu F, Yuan XH (2007) Fuzzy number intuitionistic fuzzy set. Fuzzy Syst Math 21(1):88–91
Liu H-W, Wang G-J (2007) Multi-criteria decision-making methods based on intuitionistic fuzzy sets. Eur J Oper Res 179(1):220–233. https://doi.org/10.1016/j.ejor.2006.04.009
Meng F, Tan C, Zhang Q (2013) The induced generalized interval-valued intuitionistic fuzzy hybrid Shapley averaging operator and its application in decision making. Knowl Based Syst 42:9–19. https://doi.org/10.1016/j.knosys.2012.12.006
Meng F, Tang J, Cabrerizo FJ, Herrera-Viedma E (2020) A rational and consensual method for group decision making with interval-valued intuitionistic multiplicative preference relations. Eng Appl Artif Intell 90:103514. https://doi.org/10.1016/j.engappai.2020.103514
Morente-Molinera J, Kou G, Pérez I, Samuylov K, Selamat A, Herrera-Viedma E (2018) A group decision making support system for the Web: how to work in environments with a high number of participants and alternatives. Appl Soft Comput 68:191–201. https://doi.org/10.1016/j.asoc.2018.03.047
Morente-Molinera J, Wu X, Morfeq A, Al-Hmouz R, Herrera-Viedma E (2020) A novel multi-criteria group decision-making method for heterogeneous and dynamic contexts using multi-granular fuzzy linguistic modelling and consensus measures. Inf Fusion 53:240–250. https://doi.org/10.1016/j.inffus.2019.06.028
Pawlak Z (1982) Rough sets. Int J Comput Inform Sci 11:341–356. https://doi.org/10.1007/BF01001956
Perera I (2011) Impact of poor requirement engineering in software outsourcing: a study on software developers’ experience. Int J Comput Commun Control 6(2):337. https://doi.org/10.15837/ijccc.2011.2.2182
Robertson S, Robertson J (1999) Mastering the requirements process, 2nd edn. Addison-Wesley Professional, USA
Shino TK, Sunil JJ (2012) Intuitionistic fuzzy multisets and its application in medical diagnosis. Int J Math Comput Sci 6:34–37
Smarandache F (1998) Neutrosophy/neutrosophic probability, set, and logic. American Research Press, Rehoboth
Smarandache F (2019) Neutrosophic set is a generalization of intuitionistic fuzzy set, inconsistent intuitionistic fuzzy set (Picture Fuzzy Set, Ternary Fuzzy Set), Pythagorean Fuzzy Set (Atanassov's Intuitionistic Fuzzy Set of second type), q-Rung Orthopair Fuzzy Set, Spherical Fuzzy Set, and n-HyperSpherical Fuzzy Set, while Neutrosophication is a Generalization of Regret Theory, Grey System Theory, and Three-Ways Decision (revisited), arXiv, Cornell University, New York City, NY, USA, (Submitted on 17 Nov 2019 (v1), last revised 29 Nov 2019 (this version, v2)), https://arxiv.org/ ftp/ arxiv/ papers/1911/1911.07333.pdf
Tan C (2011) A multi-criteria interval-valued intuitionistic fuzzy group decision making with Choquet integral-based TOPSIS. Expert Syst Appl 38(4):3023–3033. https://doi.org/10.1016/j.eswa.2010.08.092
Tan CQ, Ma BJ, Wu DSD, Chen XH (2014) Multi-criteria decision making methods based on interval-valued intuitionistic fuzzy sets. Int J Uncertainty Fuzziness Knowl Based Syst 22(3):475–494
Turksen I (1986) Interval valued fuzzy sets based on normal forms. Fuzzy Sets Syst 20(2):191–210. https://doi.org/10.1016/0165-0114(86)90077-1
Wang XF (2008) Fuzzy number intuitionistic fuzzy geometric aggregation operators and their application to decision making. Control Decis 23(6):607–612
Wang H, Smarandache F, Zhang YQ, Sunderraman R (2005) Interval neutrosophic sets and logic: theory and applications in computing. Hexis, Arizona
Wang H, Smarandache F, Zhang YQ, Sunderraman R (2010) Single valued neutrosophic sets. Multisp Multistruct 4:410–413
Wei G, Zhao X, Lin R (2010) Some induced aggregating operators with fuzzy intuitionistic number information and their applications for group decision making. Int J Comput Intell Syst 3(1):84. https://doi.org/10.2991/ijcis.2010.3.1.8
Weinberg GM (1972) The psychology of improved programmer performance. Datamation 82–85
Wiegers KE, Forte S, Suojanen N (2003) Software requirements, 2nd edn. Microsoft Press, Redmond
Wu J, Liu Y (2013) An approach for multiple attribute group decision making problems with interval-valued intuitionistic trapezoidal fuzzy numbers. Comput Ind Eng 66(2):311–324. https://doi.org/10.1016/j.cie.2013.07.001
Xu Z (2012) Intuitionistic fuzzy multiattribute decision making: an interactive method. IEEE Trans Fuzzy Syst 20(3):514–525. https://doi.org/10.1109/tfuzz.2011.2177466
Ye J (2014a) Prioritized aggregation operators of trapezoidal intuitionistic fuzzy sets and their application to multicriteria decision-making. Neural Comput Appl 25(6):1447–1454. https://doi.org/10.1007/s00521-014-1635-8
Ye J (2014b) Trapezoidal neutrosophic set and its application to multiple attribute decision-making. Neural Comput Appl 26(5):1157–1166. https://doi.org/10.1007/s00521-014-1787-6
Ye J (2017) Some weighted aggregation operators of trapezoidal neutrosophic numbers and their multiple attribute decision making method. Informatica 28(2):387–402. https://doi.org/10.15388/informatica.2017.108
Zadeh LA (1965) Fuzzy sets. Inf Control 8(5):338–353
Zadeh L (1975) The concept of a linguistic variable and its application to approximate reasoning—II. Inf Sci 8(4):301–357. https://doi.org/10.1016/0020-0255(75)90046-8
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Khatter, K. Interval valued trapezoidal neutrosophic set: multi-attribute decision making for prioritization of non-functional requirements. J Ambient Intell Human Comput 12, 1039–1055 (2021). https://doi.org/10.1007/s12652-020-02130-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12652-020-02130-8
Keywords
- Non-functional requirements (NFRs)
- Multi criteria decision making (MCDM)
- Multi attribute decision making (MADM)
- Neutrosophic set
- Interval valued fuzzy set (IVFS)
- Interval valued intuitionistic fuzzy set (IVIFS)
- Interval valued neutrosophic set
- Trapezoidal neutrosophic set
- Interval valued trapezoidal neutrosophic set (IVTrNS)
- Interval valued trapezoidal neutrosophic number (IVTrNN)
- Interval valued trapezoidal neutrosophic weighted arithmetic averaging operator (IVTrNWAA)