Abstract
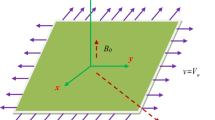
The spectral relaxation method is a very powerful tool which was applied in this paper to get the numerical solution for the system of nonlinear ordinary differential equations which describe the problem of fluid flow of a Powell–Eyring model past an exponentially shrinking sheet with the presence of magnetic field and thermal radiation. The introduced method is based on the spectral relaxation method, which is successfully used to solve this type of equations. Also, this method is developed from the Gauss–Seidel idea of reducing the governing nonlinear system of ordinary differential equations into smaller systems of linear equations. Likewise, the influences of the governing parameters on the velocity and temperature profiles are studied graphically. Results of this study shed light on the accuracy and efficiency of the proposed method in solving this type of the nonlinear boundary layer equations.





Similar content being viewed by others
References
S S Motsa and Z G Makukula Cent. Eur. J. Phys. 11 363 (2013)
S Shateyi Bound. Value Probl. 196 1 (2013)
D Vieru and C Fetecau Appl. Math. Comput. 200 459 (2008)
T Hayat, Z Iqbal, M Qasim and S Obaidat Int. J. Heat Mass Transf. 55 1817 (2012)
N S Akbar and S Nadeem Heat Mass Transf. 46 531 (2010)
M M Khader Indian J. Phys. 11 1 (2019)
J C Pu and H C Hu Indian J. Phys. 93 229 (2019)
M Y Malik, A Hussain and S Nadeem Sci. Iran. Trans. Mech. Eng. (B) 20 313 (2013)
F Awad, S S Motsa and M Khumalo PLoS ONE 9 16 (2014)
N A Haroun, P Sibanda, S Mondal and S S Motsa Bound. Value Probl. 23 210 (2015)
S S Motsa Chem. Eng. Commun. 12 107 (2013)
C Canuto, M V Hussaini, A Quarteroni and T A Zang Spectral Methods in Fluid Dynamics (Berlin: Springer) (1988)
L N Trefethen Spectral Methods in MATLAB (Philadelphia: SIAM) (2000)
P K Kameswaran, P Sibanda and S S Motsa Bound. Value Probl. 242 1 (2013)
S S Motsa, P Dlamini and M Khumalo Nonlinear Dyn. 72 265 (2013)
S S Motsa, P G Dlamini and M Khumalo Adv. Math. Phys. 2014 Article ID 341964 (2014)
A Ara, N A Khan, H Khan and F Sultan Ain Shams Eng. J. 5 1337 (2014)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Khader, M.M. Numerical solutions for the problem of the boundary layer flow of a Powell–Eyring fluid over an exponential sheet using the spectral relaxation method. Indian J Phys 94, 1369–1374 (2020). https://doi.org/10.1007/s12648-019-01583-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12648-019-01583-8