Skip to main content
SpringerLink
Log in

Axial vibration of single-walled carbon nanotubes with fractional damping using doublet mechanics

  • Original Paper
  • Published:
Indian Journal of Physics Aims and scope Submit manuscript

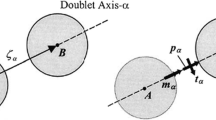
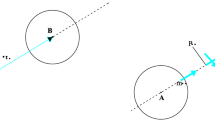
Abstract

This paper investigates the axial vibration of single-walled carbon nanotubes (SWCNTs) with fractional damping based on doublet mechanics. The Kelvin–Vigot model is used to incorporate damping effect for CNTs. By solving the equation of motion, the relation between natural frequency with scale parameter and fractional order is derived in the axial mode of vibration. It is shown that fractional order and scale parameter play significant roles in the axial vibration behavior of SWCNTs. Such effects decrease the natural frequency compared to the predictions of the classical continuum mechanics models and also ignores the damping effects. These effects on the natural frequency are more apparent in higher mode numbers and lower tube lengths and radii. Results for complex roots of characteristic equation obtained for a SWCNT without viscoelastic foundation, where imaginary parts represent damped frequencies, were compared with the results found from molecular mechanics simulations and a good agreement was achieved.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. M Ferrari, V T Granik, A Imam and J Nadeau Advances in Doublet Mechanics (Berlin: Springer) (1997)

    Book  Google Scholar 

  2. A Fatahi-Vajari and A Imam ZAMP89 81 (2016) https://doi.org/10.1007/s00033-016-0675-6

    Article  ADS  Google Scholar 

  3. A C Eringen Int. J. Eng. Sci.10 1 (1972)

    Article  Google Scholar 

  4. A Szabó et al. Materials3 3092 (2010)

    Article  ADS  Google Scholar 

  5. F Taleshi, A A Hosseini, M Mohammadi and M Pashaee Indian J. Phys.87 873 (2013)

    Article  ADS  Google Scholar 

  6. A Fatahi-Vajari and A Imam Indian J. Phys.90 447 (2016)

    Article  ADS  Google Scholar 

  7. S M Bachilo et al. Science298 2361 (2002)

    Article  ADS  Google Scholar 

  8. D Sanchez-Portal, E Artacho, J M Soler, A Rubio and P Ordejon Phys. Rev. B59 12678 (1999)

    Article  Google Scholar 

  9. S S Gupta, F G Bosco and R C Batra Comput. Mater. Sci.47 1049 (2010)

    Article  Google Scholar 

  10. S S Gupta and R C Batra Comput. Mater. Sci.43 715 (2008)

    Article  Google Scholar 

  11. S S Rao Vibration of Continuous Systems (New Jersey: Wiley) (2007)

  12. M H Sadd Elasticity Theory, Applications, and Numerics (Burlington: Elsevier Butterworth-Heinemann) (2005)

  13. U Gul, M Aydogdu and G Gaygusuzoglu Compos. Struct.160 1268 (2017)

    Article  Google Scholar 

  14. A Fatahi-Vajari, A Imam J. Solid Mech.8 875 (2016)

    Google Scholar 

  15. U Gul and M Aydogdu Compos. Part B Eng.137 60 (2018)

    Article  Google Scholar 

  16. A Fatahi-Vajari and A Imam ZAMM96 1020 (2016)

    Article  ADS  Google Scholar 

  17. V T Granik and M Ferrari Mech. Mater.15 301 (1993)

    Article  Google Scholar 

  18. M Kojic, I Vlastelica, P Decuzzi, V T Granik and M Ferrari Comput. Methods Appl. Mech. Eng.200 1446 (2011)

    Article  ADS  Google Scholar 

  19. F Gentile, J Sakamoto, R Righetti, P Decuzzi and M Ferrari J. Biomed. Sci. Eng.4 362 (2011)

    Article  Google Scholar 

  20. M Ferrari Biomed. Microdevices2 273 (2000)

  21. J Xin, L Xiao-Zhou and W Jun-Ru Chin. Phys. Lett.26 074301-1 (2009)

    ADS  Google Scholar 

  22. S S Lin and Y C Shen Soil Dyn. Earthq. Eng.25 893 (2005)

    Article  Google Scholar 

  23. M H Sadd and Q Dai Mech. Mater.37 641 (2005)

    Article  Google Scholar 

  24. G Mandal and T Ganguly Indian J. Phys.85 1229 (2011)

    Article  ADS  Google Scholar 

  25. F Maddalena and M Ferrari Mech. Mater.20 241 (1995)

    Article  Google Scholar 

  26. A Fatahi-Vajari and Z Azimzadeh Indian J. Phys.92 1425 (2018)

    Article  ADS  Google Scholar 

  27. U Gul and M Aydogdu J. Mech.34 279 (2018)

    Article  Google Scholar 

  28. A Fatahi-Vajari ZAMM98 255 (2018)

    MathSciNet  Google Scholar 

  29. M Imboden and P Mohanty Phys. Rep.534 89 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  30. A M Dıez-Pascual, M A Gomez-Fatou, F Ania and A Flores Prog. Mater. Sci.67 94 (2015)

    Google Scholar 

  31. T M Atanackovic, S Pilipovic, B Stankovic and D Zorica Fractional Calculus with Applications in Mechanics (London: Wiley) (2014)

    Book  Google Scholar 

  32. J F Gomez-Aguilar, J J Rosales-Garcıa, J J Bernal-Alvarado, T Cordova-Fraga and R Guzman-Cabrera, Revista Mexicana de Física58 348 (2012)

    Google Scholar 

  33. M Borowiec, G Litak and A Syta Shock Vib.14 29 (2007)

    Article  Google Scholar 

  34. Y Lei, T Murmu, S Adhikari and M I Friswell Eur. J. Mech. A/Solids42 125 (2013)

    Article  ADS  Google Scholar 

  35. D Karlicic, M Cajic, T Murmu and S Adhikari Eur. J. Mech. A/Solids49 183 (2015)

    Article  ADS  Google Scholar 

  36. A H Ghorbanpour-Arani, A Rastgoo, M M Sharafi, R Kolahchi and A G Arani Meccanica51 25 (2016)

    Article  Google Scholar 

  37. R L Bagley and P J Torvik J. Rheol. (1978-present)30 133 (1986)

  38. W J Welch, R A Rorrer and R G Duren Mech. Time-Dependent Mater.3 279 (1999)

    Article  ADS  Google Scholar 

  39. Y A Rossikhin and M V Shitikova Mech. Time-Dependent Mater.5 131 (2001)

    Article  ADS  Google Scholar 

  40. A Tofighi Physica A329 29 (2003)

    Article  ADS  Google Scholar 

  41. J F Gómez-Aguilar et al. Entropy17 6289 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  42. A W Wharmby and R L Bagley J. Rheol. (1978-present)57 1429 (2013)

  43. T D Shermergor J. Appl. Mech. Tech. Phys.7 85 (1966)

    Article  ADS  Google Scholar 

  44. R Ansari, M F Oskouie, F Sadeghi and M Bazdid-Vahdati Physica E74 318 (2015)

    Google Scholar 

  45. R Ansari, M F Oskouie and R Gholami Physica E75 266 (2016)

    Google Scholar 

  46. N Challamel, D Zorica, T M Atanackovic and DT Spasic Comptes Rendus Mécanique341 298 (2013)

  47. M Cajic, D Karlicic and M Lazarevic Meccanica (2017) https://doi.org/10.1007/s11012-016-0417-z

  48. M Cajic, D Karlicic, and M Lazarevi Theor. Appl. Mech.42 167 (2015)

    Article  ADS  Google Scholar 

  49. I Podlubny Fractional Differential Equation (San Diego: Academic Press) (1999)

  50. A A Kilbas, H M Srivastava and J J Trujillo Theory and Applications of Fractional Differential Equation (Amsterdam: Elsevier) (2006)

    Google Scholar 

  51. Y Povstenko Linear Fractional Diffusion-Wave equation for Scientists and Engineers (New York: Birkhauser) (2015)

  52. Y. Povstenko J. Therm. Stress.39 1442 (2016)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Young Researchers and Elite Club, Yadegar-e-Imam Khomeini (RAH) Shahr-e-Rey Branch, Islamic Azad University, Tehran, Iran

    Alireza Fatahi-Vajari & Zahra Azimzadeh

Authors
  1. Alireza Fatahi-Vajari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zahra Azimzadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alireza Fatahi-Vajari.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fatahi-Vajari, A., Azimzadeh, Z. Axial vibration of single-walled carbon nanotubes with fractional damping using doublet mechanics. Indian J Phys 94, 975–986 (2020). https://doi.org/10.1007/s12648-019-01547-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12648-019-01547-y

Keywords

PACS Nos.

Search

Navigation