Introduction

Heart failure is a challenging health problem with increasing prevalence throughout the globe. As a matter of fact, despite all advances in cardiovascular science and technology, heart failure is still one of the major causes of death [23]. Pathological cardiac hypertrophy, as a known important risk factor in heart failure, develops with the increment of biochemical and mechanical stimuli. At the cellular level, these stimuli are transduced to hypertrophy-responsive transcription factors through a complex network of signaling pathways [27, 28]. The β-adrenergic signaling pathway is one of the pathways that mediate cardiac hypertrophy and plays a central role in all pathophysiological aspects of heart failure [20, 37]. According to the literature, chronic stimulation of β-adrenergic receptors (β-ARs) by agonists such as isoproterenol (ISO) could induce cardiac hypertrophy [7, 43].

The β-ARs are a class of the superfamily of membrane proteins known as G-protein-coupled receptors (GPCRs) including four subtypes [31]. The most important β-AR subtypes are β1-AR and β2-AR, which comprise 75–80% and 20–25% of cardiac β-ARs, respectively [47, 64]. Some studies claim that β-AR-induced hypertrophy is mainly caused by the β1-AR subtype stimulation [43, 53]. However, the decrease in the ratio of β1/β2 receptors and the significant increase of Giα level in a failing heart [10, 11, 22] suggest a key role of the β2-AR stimulation in cardiac hypertrophy and heart failure [58]. The β-adrenergic signaling pathway can be divided into two subdivisions: classical and non-classical [37]. In the classical pathway, which is shared between β1-AR and β2-AR, ligand binding activates adenylyl cyclases (AC) through Gs, causing a rise in the cellular concentration of cyclic AMP (cAMP) and subsequent stimulation of protein kinase A (PKA) [30]. The non-classical pathway, which is specific to β2-AR, is initiated by PKA-mediated switching of β2-AR coupling from Gs to Gi. Then, the ligand binding activates the two main signaling pathways through Gi: PI3 K/Akt/GSK3β and Ras/Raf/MEK/ERK [37, 52]. At the downstream of both classical and non-classical signaling pathways, there are transcription factors such as cAMP response element-binding protein (CREB) [12] and GATA binding protein 4 (GATA4) [42], which facilitate hypertrophic gene expression. Despite successful investigations for identification of the β-adrenergic signaling components, the complexity of this network makes the understanding of its signaling responses difficult.

Most of the efforts to understand the signaling network of β-AR-induced hypertrophy are experimental studies that investigate isolated pathways [49]. Although in vitro and in vivo experiments elucidate the main characteristics of β-adrenergic signaling [50], they have limitations, such as the inability to recognize the relative contribution of its hypertrophic mediators in cardiac morphological and biochemical changes. In general, qualitative and experimental approaches are not sufficient for investigating complex nonlinear networks such as the signaling network of β-AR-induced hypertrophy [27]. Quantitative understanding of these biological networks is a challenging issue, which can be accomplished by computational systems models [17]. Saucermann et al. [51] presented the first mathematical model for the β1-adrenergic pathway to analyze the effects of β-adrenergic signaling on myocyte excitation-contraction coupling. Since then, researchers have proposed several mathematical models for β-AR classical signaling pathway in cardiac myocytes [9, 26, 29, 32, 63]. However, the majority of these studies have investigated non-hypertrophic functions of β-adrenergic signaling pathway. There are a few studies that have addressed the modeling of β-AR-induced hypertrophy. In one of them, Yang et al. [66] extended Saucerman et al.’s [51] model for β1-adrenergic signaling, classical pathway, to study the protein kinase A activity in the cytosol and the nucleus and investigated the effects of protein kinase A on CREB activity. In another study, Ryall et al. [48] presented a general model for cardiac hypertrophy signaling network including the β-adrenergic pathway. Despite that their model considers nearly all the pathways which contribute in cardiac hypertrophy, it has a limitation in capturing the dynamics of hypertrophic mediators. This limitation is due to the lack of valid experimental data for all signaling pathways, which makes them to use the same default parameters for all reactions. So, their model is practically a logic-based network model, not a deterministic one.

In this study, we present a computational model for β-adrenergic-induced hypertrophy. The model covers both classical and non-classical signaling pathways that are shown to be effective in β-AR-induced cardiac hypertrophy. In order to develop the model, we first identify unknown intermediate components of β-adrenergic non-classical signaling pathway based on the experimental results reported in previous studies [39, 41, 67, 69]. We then determine the kinetic reaction parameters either from the existing kinetic data or from fitting the simulated results to experimental data. To achieve a coherent model, we take into account important phenomena such as β-AR desensitization and cross-talk between signaling pathways. In this study, the proposed model is validated by relevant experimental data. This model can be used to investigate the β-AR-induced activation of cardiomyocyte hypertrophic transcription factors such as CREB and GATA4 and analyze the mediators’ contribution in this response.

Materials and methods

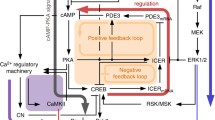
The purpose of this study is to model the β-AR signaling pathways involved in cardiac hypertrophy. Since both classical and non-classical β-AR pathways play a crucial role in β-AR-induced hypertrophy [4, 37], we considered both cases to define the topology of our model. Figure 1 represents the general pathways involved in our model and the cross-talk between them. The detailed schematic diagram of non-classical pathways is illustrated in Fig. S1 (supplementary materials). The model has one cellular compartment in which the β-ARs are the upstream and the transcription factors CREB and GATA4 are the downstream of the pathways. The comprehensive description of our model with its equations and parameters are presented in supplementary materials.

Fig. 1
figure 1

The model of β2-AR signaling pathways involved in the cardiac hypertrophy. The left is classical and the right is non-classical β-adrenergic pathway. Activation and inhibition of the components are indicated by arrows and T-bars, respectively

Full size image

To construct the model, the biochemical reactions in each pathway should be first formulated for which we used ordinary differential equations (ODEs) based on the mass action and Michaelis–Menten kinetics. To formulate enzymatic reactions with common enzymes such as PP2A, MEKPP, and Ras-GTP, we used the equations that are presented in Hatakeyama et al.’s [25] study. To obtain the required kinetic parameters, we utilized cardiomyocyte kinetics and experimental data of rats as far as possible (see supplementary materials). The reasons for the selection of rat data for our model are as follows: rat is a valid model system for studying cardiovascular changes in humans such as cardiac hypertrophy [19] and most of the experimental research related to cardiac hypertrophy is conducted on rat cardiomyocytes.

In modeling biological pathways, there is often a trade-off between simplicity and completeness. Simple models are easy to handle, but, for the large and complex signaling networks such as β-adrenergic, there are limitations for their applicability. Consequently, these models cannot capture the underlying dynamics in the β-adrenergic network. Thus, to capture the most features of the β-adrenergic pathways, it was inevitable to build a complex model. One of the main difficulties in developing large and complex models is the lack of coordination between the number of experimental observations and model parameters. This disproportion may result in the model non-identifiability and overfitting. So, we took several approaches to minimize the possibility of these shortcomings.

First, by a comprehensive and detailed review of the literature on signaling network of β-AR-induced hypertrophy (see supplementary materials), we identified the most effective signaling components. Therefore, in our model, we only took into account the components that their effects on β-AR-induced hypertrophy have been established. Second, we obtained as many parameters as possible from the literature to reduce the number of estimated parameters. Also, based on the previous computational and experimental studies, we made several assumptions to simplify the model equations and reduce its parameters. For example, in the receptor module, we assumed that the hydrolysis and reassociation rates are equal for Gs and Gi proteins and PKA-mediated desensitization of β1-AR and β2-AR subtypes are related (Table S2). Third, to avoid overfitting, it is necessary to test the model’s ability to generalize to unseen data by assessing its performance on a set of data that is not used for calibration. So, in the Results section, we externally validated our model and evaluated its generality by comparing the model’s results with experimental data that were not used for calibration.

In summary, the presented model captures the concentration of 39 signaling components as state variables (Table S1). Also, the unknown model parameters, which must be estimated from fitting the model results to the experimental data (calibration process), are 40 parameters (Table S2–S9). For calibration and validation of our model, we used experimental data of 15 signaling components of our model (71 experimental point data for calibration and 100 experimental point data for validation).

After completing our model structure, we investigated its identifiability. Due to the size and complexity of the model, the designed methods and software in the literature to check the model global identifiability were powerless mainly due to computational costs (e.g., lack of memory in GenSSI [14] in a PC with Intel Core i7 CPU and 32 GB RAM). Finally, by applying an algorithm [3], which is suited for the large and complex models (only check local identifiability), we determined that our model is locally structurally identifiable.

According to the model topology, β-adrenergic non-classical pathways are downstream of the classical pathway without any feedback to the upstream. There is also the same connection between the transcription factors module and the classical and non-classical pathways. So, it is not necessary to estimate all of the unknown parameters at once. First, we estimated the parameters of the classical pathway and subsequently the parameters of non-classical pathways from related experimental data. Finally, we estimated the parameters of transcription factors module. Inspired by the performance of hybrid approaches, we used a hybrid approach to minimize objective function value that is sum of the squared residuals between experimental measurements and the model trajectories. We used an evolutionary algorithm (genetic algorithm) to explore the parameters space for highest scoring parameters. The parameters’ bounds have been determined by physiological consideration (positive rate constant and concentrations) or centered on the values from previous models. We then used a nonlinear least-square solver (trust-region method) with highest score sets of parameters as initial values to reach the minimal objective function value. To diminish the risks of getting trapped in a local minimum, we also randomly changed some of the initial values from each set. The estimation process was conducted in MATLAB. We also selected root mean squared error (RMSE) for the goodness-of-fit measure. Since this measure has the same unit with experimental data, we could compare RMSE with the experimental measurement errors to obtain the goodness-of-fit. In Fig. 2, the RMSE for fitted curves (except Fig. 2e) are below or equal to experimental measurements errors. So, our model is reasonably well fitted to experimental data.

Fig. 2
figure 2

Estimation of kinetic parameters for β-adrenergic classical and non-classical signaling pathways. a The sensitivity of normalized AC activity over basal to isoproterenol for maximal AC activity (simulation solid line and experimental filled circle) and AC activity after 30 min of ISO stimulation (simulation dashed line and experimental filled triangle). The experimental data were obtained from Freedman et al.’s study [21] for β1-AR stimulation and its desensitization through GRK2 mechanism. b The time course of normalized cAMP level after indicated ISO stimulation. The experimental data were obtained from De Arcangelis et al.’s study [18]. c The time course of normalized PKA activity after indicated ISO stimulation. The experimental data were obtained from De Arcangelis et al.’s study [18]. d The time course of normalized active GSK3β after indicated ISO stimulation. The experimental data were obtained from Morisco et al.’s study [41]. e The time course of normalized active Shc after indicated ISO stimulation. The experimental data were obtained from Zou et al.’s study [69]. f The time course of normalized ERK1/2 pp concentration after indicated ISO stimulation. The experimental data were obtained from Shin et al.’s study [56]. g The sensitivity of normalized steady-state activity of CREB to isoproterenol. The experimental data were obtained from Yang et al.’s study [66]. h The time course of normalized GATA4 activity after indicated ISO stimulation. The experimental data were obtained from Morisco et al.’s study [42]. For b–h, simulation results are indicated by solid lines and experimental data are indicated by filled circles. The experimental data are mean ± SE of at least three independent experiments

Full size image

After constructing the model, the system of ordinary differential equations of our model is solved in MATLAB using the ode15 s solver. To obtain initial conditions for the state variables of the model, we ran the model to steady-state without ISO stimulation. The state variables of the model and their initial conditions are shown in Table S1 (supplementary materials). As shown in Fig. 2, the model outputs fit reasonably well to the experimental data.

Results and discussion

In this study, we constructed a computational model to investigate different mediators’ response to β-ARs stimulation and their contribution in the β-AR-induced cardiac hypertrophy. The model involves two main signaling pathways: classical and non-classical pathways. In the following, we investigate the dynamic response of the pathway components to β-ARs stimulation and utilize a sensitivity analysis to realize the main controlling parameters in the β-AR-induced cardiac hypertrophy.

Dynamics of the classical pathway activity during β-ARs stimulation

The β-adrenergic classical pathway connects the β-ARs stimulation to cardiac excitation-contraction coupling by AC/cAMP/PKA pathway. The pathway also mediates hypertrophic signals by several known methods. First, PKA could directly activate hypertrophic transcription factors such as CREB. Second, β2-AR phosphorylation by PKA initiates β2-AR switching from Gs to Gi and subsequent β-adrenergic non-classic signaling. Third, PKA controls both cardiomyocyte calcium transient and diastolic level by phosphorylation of ryanodine receptor, L-type calcium channel, and phospholamban [6]. The modification of intracellular calcium by PKA could induce cardiac hypertrophy by activating the Ca2+-dependent pathways [66] such as CaN/NFAT. In this study, we model the two first methods of transducing hypertrophic signals by the classical pathway.

We investigate the dynamics of the classical pathway activity during β-ARs stimulation, first, by examining the phosphorylation (desensitization) of β-ARs by both PKA and GRK2. The model is calibrated to reproduce the experimental results related to human β1-AR desensitization through GRK2 mechanism [21], see Fig. 2a. We simulated this experiment by setting the total β2-AR and PKA concentration equal to zero in our model. According to the result, pretreatment of CHW cells with ISO for 30 min both in vitro and in silico, reduce the maximal AC activity resulted from β1-AR stimulation (ISO = 1 µM) to 55% of its value in control. Also, we determined the contribution of PKA in β1-AR desensitization by simulating β1-AR phosphorylation by ISO as seen in Fig. 3a.

Fig. 3
figure 3

The β-ARs desensitization by isoproterenol. a Phosphorylation of β1-AR by ISO through GRK2 and PKA. The experimental data were obtained from Freedman et al.’s study [21] for HEK293 cells with and without PKA inhibitor (H89) after 3-min ISO stimulation. b Desensitization of β2-AR by ISO after different ISO concentration and stimulation times. The experimental data were obtained from Lohse et al.’s study [36] for A431 cells with and without PKI (1 µM). The experimental data are mean ± SE of at least three independent experiments

Full size image

According to Freedman et al.’s study [21], pretreatment of intact 293 cells with H89, a PKA inhibitor, attenuates the β1-AR phosphorylation by 65%, which is in agreement with our model results. Moreover, they showed that pretreatment of CHW cells with transfected β2-AR in 1 µM ISO-containing medium for 5 min reduces the maximal AC activity to about 70% of its value in control after stimulation with different isoproterenol concentrations (0.1, 0.3, and 1 µM) and through GRK2 mechanism. We simulated this experiment by setting the total β1-AR and PKA concentration to zero and applying ISO (1 µM) for 5 min to obtain new initial conditions for subsequent simulations. The calculated maximal AC activity is about 73% of maximal AC activity of control, which is consistent with the experimental results. In β-ARs desensitization, especially β2-AR, β-ARs phosphorylation by PKA has minimum effects at longer times after agonist stimulation or at high agonist concentrations [62]. As shown in Fig. 3b, pretreatment of cells with ISO at short times or low concentrations results in the elevation of PKA contribution in β2-AR desensitization. Therefore, it seems that β2-AR desensitization through GRK2 is more important than its desensitization by PKA in the hypertrophied and failing hearts with chronic isoproterenol stimulation [15].

In the classical β-adrenergic pathway, adenylyl cyclases are in charge of converting ATP to cAMP. We considered a basal level for AC activity along with its activation and inhibition by Gsα and Giα in our model, respectively. As shown in Fig. 2a, we adjusted the model parameters to fit the simulated results to the experimental data of AC activation above basal level for different ISO concentrations in CHW cells with transfected β1-AR. To investigate the model’s ability to resemble cardiomyocyte experimental data, we determined AC activity above basal level as a function of isoproterenol concentration through the model. As seen from Fig. 4, the model could replicate the sensitivity of AC activity to isoproterenol in mouse ventricular and cardiac cells.

Fig. 4
figure 4

Normalized AC activity above basal level after ISO stimulation at different concentrations. The simulation result is indicated by a solid line and experimental data for mouse hearts [59] and ventricular myocytes [33] are indicated by filled circles and hollow triangles, respectively. The experimental data represent mean ± SE from five individual experiments

Full size image

Cyclic AMP is one of the main mediators in the β-adrenergic classical pathway [61]. In addition to AC, PDEs also contribute in the regulation of cAMP level by degrading cAMP into 5′-AMP. The PKA-mediated phosphorylation of PDEs could enhance its activity several fold. As seen from Fig. 2b, cAMP level rises to its maximum in 1–3 min [1, 18] after ISO stimulation due to the activation of AC by β-adrenergic receptors. The increased level of cAMP leads to the enhanced PKA activity and subsequent PDEs phosphorylation. The phosphorylation of PDEs by PKA and elevation of cAMP level increase the rate of cAMP degradation by PDEs. Also, the AC activity decreases through time due to the desensitization of the β-adrenergic receptors. These events result in the reduction of cAMP level from its maximum to a steady-state level. Figure 5a indicates the basal level and accumulation of cyclic AMP in the model and mouse cardiomyocytes at different times after ISO stimulation. The resting concentration of cAMP in our model is 0.683 µM that is in the range of basal cAMP level in the cardiac cells (0.5–1 µM) [9]. To convert the biological numbers such as protein concentrations from pmol/mg cell protein to µM in a cardiac cell, we used conversion factors of Table 9 from Ref. [6].

Fig. 5
figure 5

Effects of β-ARs stimulation by isoproterenol on the cellular cAMP level. a The cAMP accumulation in cardiomyocytes after ISO stimulation. The experimental data were obtained from O’Connell et al.’s study [44] for mouse cardiac myocytes and are mean ± SE of three independent experiments. b Effects of β-AR subtype specific-antagonists and PDEs inhibitor, IBMX, (100 µM) on the cellular cAMP level. The experimental data were obtained from Rochais et al.’s study [46] for rat ventricular myocytes after 3 min ISO stimulation and represent mean ± SE of at least eight separate experiments

Full size image

Also, we included the effects of IBMX, as a non-specific PDEs inhibitor, on β-adrenergic pathway activity in our model to examine the impacts of PDEs on the cAMP level. Figure 5b shows both simulated and experimental data of cAMP level with and without IBMX. IBMX inhibits PDEs and raises both basal and ISO-induced cAMP level in the cardiac cells. In addition to the isoproterenol, we utilized the β-AR subtype-specific antagonists’ data to study the impact of each subtype on ISO-induced cAMP accumulation in cardiac cells. ICI and CGP are selective β2-AR and β1-AR antagonists, respectively. We simulated the β-AR stimulation via its antagonists by setting the total concentration of related β-AR subtype to zero in our model. The predictions of cAMP level with and without IBMX compare well with the experimental data. According to Fig. 5b, β1-AR stimulation by ISO has a greater impact on cAMP level in comparison to the β2-AR stimulation, which is inconsistent with experimental observations [57].

Protein kinase A is the downstream component of the β-adrenergic classical pathway and is responsible for most of its physiological and pathological functions. Activation of PKA holoenzymes by cAMP releases the PKA catalytic subunits, which phosphorylate many cell components including ion channels and proteins involved in the cardiomyocytes Ca2+ handling system. Figure 6a illustrates the PKA activity as a function of cellular cAMP concentration with and without heat-stable protein kinase inhibitor (PKI). As seen from Fig. 6a, PKI inhibits PKA completely in cellular cAMP concentrations below 100 nM and its inhibitory effect diminishes PKA activity to 80% of its maximum in high cellular cAMP concentrations. The simulated variations of PKA activity as a function of cAMP concentration fit well with the experimental data in both cases.

Fig. 6
figure 6

The PKA activity after β-ARs stimulation by ISO (a) normalized PKA activity as a function of cAMP level with (simulation dashed line and experimental hollow triangle) and without PKI (1 µM) (simulation solid line and experimental filled circle). The experimental data were obtained from Beavo et al.’s study [5]. b The time course of normalized PKA activity after indicated ISO stimulation. The experimental data were obtained from Amanfu and Saucerman’s study [2] for cardiac myocytes. In a and b, no error bar was provided for experimental data in references. c The time course of normalized PKA activity after indicated ISO stimulation. The experimental data were obtained from De Arcangelis et al.’s study [18] for cardiac myocytes and are mean ± SE from three separate experiments

Full size image

The time courses of cellular PKA activity are shown in Fig. 6b, c for different ISO concentrations. We considered the cellular concentration of PKA catalytic subunits (PKAC) as PKA activity. As is evident from Fig. 6b, c, the PKA activity reaches its maximum in 1–2 min after ISO stimulation and then declines slowly to its steady-state level. The dynamics of PKA activity is similar to the cAMP level.

Due to the importance of PKA in both β-adrenergic classical and non-classical signaling, we simulated the time course of ISO-induced PKA activity (catalytic subunits concentration) by four isoproterenol concentrations, 10, 100, 1, and 10 µM, in the presence of different β-AR subtypes to investigate the impacts of β-AR subtypes on PKA activity. As is clear from Fig. 7, in low concentrations of isoproterenol (10 nM), β1-AR and β2-AR subtypes have relatively equal influence on PKA activity; however, in high isoproterenol concentrations, the role of β1-AR in PKA activity becomes more dominant. According to the results of Yang et al. [66], in ISO-induced myocyte hypertrophy, EC50 is 86 nM and maximal hypertrophy could be obtained by 1 µM ISO. The ratio of the PKA activity that is induced by β1-AR stimulation to β2-AR stimulation varies from 2.6:1 for 86 nM ISO to 4:1 for 1 µM ISO in the model. Hence, the role of β2-AR in ISO-induced hypertrophy cannot be ignored even in the healthy cardiomyocytes with the molar ratio 5:1 for β1-AR to β2-AR.

Fig. 7
figure 7

The simulated PKA activity after different indicated ISO stimulation. Simulated time courses of PKAc concentration for control condition (normal cardiomyocytes), selective β1-AR and β2-AR stimulation are shown by solid, dashed, and dotted lines, respectively

Full size image

Dynamics of the non-classical pathway activity during β-ARs stimulation

PI3K/Akt/GSK3β and Ras/Raf/MEK/ERK are two pathways that are included in the β-adrenergic non-classical signaling pathway. In the PI3K/Akt/GSK3β pathway, GSK3β acts as a known negative regulator of cardiac hypertrophy. Activation of this pathway by β2-AR-Gi complex inhibits GSK3β and leads to cardiac hypertrophy by releasing the inhibitory effects of GSK3β on several hypertrophic transcription factors such as GATA4 and CREB. In the Ras/Raf/MEK/ERK pathway, stimulation of β2-AR-Gi coupling leads to the ERK1/2 phosphorylation. Phosphorylated ERK1/2 contributes to cardiac hypertrophy by facilitating hypertrophic gene expression through GATA4 activation. These two pathways are closely attached together with several interrelations that are shown in Fig. S1.

In the non-classical pathway, PI3K plays an important role in mediating hypertrophic signal to both Akt and ERK. In Fig. 8a, ISO-induced PI3K activity is illustrated. Cellular PIP3 concentration was measured as PI3K activity in both model and experimental studies. As seen from Fig. 8a, our model predictions for PI3K activity are consistent with cardiomyocyte experimental data after ISO stimulation with and without CGP antagonist. While β2-AR is the recognized β-AR subtype responsible for PI3 K activation [13], β1-AR also contributes to PI3K activation due to its role in PKA-mediated phosphorylation of β2-AR. Figure 8a illustrates the major role of β2-AR stimulation in PI3 K activity. In this regard, in silico blocking of β2-AR stimulation results in the complete suppression of ISO-induced PI3K activity, which is similar to the experimental observations [13]. Also, inhibition of Giβγ abolishes the PI3K activity, which is consistent with Yano et al. study [67]. They showed that Gβγ inhibition eliminates both basal and ISO-induced PI3K activity in the cardiomyocytes. The simulated time course of PIP3 concentration, as a measure of PI3K activity, is shown for different ISO concentration in Fig. 8b. Cellular PIP3 concentration elevates to its maximum after ISO stimulation in 2 min and then gradually declines to its steady-state level in 1 h.

Fig. 8
figure 8

The effect of β-AR stimulation by ISO on PI3 K activity. a The β-AR-induced increase in PI3 K activity after 2-min stimulation by ISO with and without CGP antagonist. The experimental data were obtained from Yano et al.’s study [67] for H9c2 cardiomyocytes and represent mean ± SE from three separate experiments. b The simulated time course of PIP3 concentration after stimulation with different isoproterenol concentrations (0.001 µM filled circle, 0.01 µM filled diamond, 0.1 µM filled triangle, 1 µM star and 10 µM hollow square)

Full size image

Akt (PKB) is a serine/threonine protein kinase that is activated by PDK1. The experimental studies on cardiomyocytes show that phosphorylated Akt at Thr308 (Akt-p) reaches its peak within 5 min after ISO stimulation and then decreases to the steady-state level [16], which is similar to our model results. The calculated cellular concentration of ISO-induced phosphorylated Akt at Thr308 by the model is compared to the cardiomyocyte experimental data in Fig. 9a.

Fig. 9
figure 9

Effects of β-AR stimulation on Akt and GSK3β activity. a ISO-induced Akt phosphorylation at Thr308. The increase in Akt phosphorylation after stimulation by ISO for 2 min EXP1 and 30 min EXP2. The experimental data were obtained from Yano et al.’s study [67] for H9c2 cardiomyocytes (EXP1) and from Zhang et al.’s study [68] for mouse cardiac cells (EXP 2). The experimental data represent mean ± SE from three (EXP1) and six (EXP2) individual experiments. b ISO-induced Akt-pp kinase activity. The experimental data were obtained from Morisco et al. study [41] for rat cardiac myocytes and represent mean ± SE from four separate experiments. c GSK3β phosphorylation (deactivation) after ISO stimulation through PI3 K/Akt pathway. The experimental data were obtained from Zhang et al.’s study [68] for mouse cardiac cells at 30 min after ISO stimulation. Data are mean ± SE from six individual experiments

Full size image

The double phosphorylation is necessary for complete activation of Akt. The simulated activity of Akt-pp is validated through measuring GSK3 phosphorylation by Akt-pp in both model and experimental study, as seen in Fig. 9b. Also, The cellular concentration of phosphorylated GSK3β after ISO stimulation in both model and mouse hearts are shown in Fig. 9c. As is clear from Figs. 9c and 2d, ISO-induced activation of Akt results in the GSK3β phosphorylation and reduces the active GSk3β concentration.

In the ERK pathway, both Giα and Giβγ (through PI3 K) activate Src that is the responsible mediator for the activation of downstream components of the ERK1/2 pathway [60]. According to the experimental data [39, 40] after isoproterenol stimulation, active Src concentration rises to five- six-folds of its basal concentration in 2 min. Nevertheless, its concentration is too low (below 2–3%) compare to the Src total concentration [38]. The measured ratio of active Src to total Src concentration in our model and experimental data are displayed in Fig. 10. For the remaining mediators of ERK pathway except ERK1/2, there are a few valid experimental data for their activation after ISO stimulation and most of them are qualitative. So, we validate our model results qualitatively. In this regard, the overall time courses of the ERK pathways components in our model are similar to experimental observations. They reach their maximum in a short time and gradually decrease to their steady-state values through time. In our model for different ISO stimulation, the peak times of active Src, active Shc, Shc-GRB2 complex, Ras-GTP, active Raf, and ERK1/2 pp are within 2–3 min, 2–3 min, 2–3 min, 2–3 min, 0.5–1 min, and 3–7 min after ISO stimulation, respectively. These peak times are in good consistency with experimental observations on ERK pathways in cardiomyocytes [16, 54, 69, 70].

Fig. 10
figure 10

Activation of Src after indicated ISO stimulation. The experimental data were obtained from Luttrell et al.’s study [38] for HEK 293 cells and are mean ± SE of three independent experiments

Full size image

ERK1/2 is the downstream component of Ras/Raf/MEK/ERK pathway and plays the major role in cardiac hypertrophy. ERK1/2 is activated through double phosphorylation by MEKpp. Several mediators are suggested in previous studies for contribution to ISO-induced ERK activation in cardiac myocytes. For example, Zou et al. [69] showed that PKA is involved in ERK activation by ISO. So, we simulated ERK activation by ISO with and without PKA inhibition. The results are shown in Fig. 11a and have good consistency with experimental data of rat hearts. In addition to PKA, inhibition of Gi, Gβγ and Src by Pertussis toxin (PTX), overexpression of βARK1495−689 and Csk, respectively, suppresses the ISO-induced ERK activity in vitro [69], which are also predicted by the model. Wortmannin is a potent non-specific PI3 K inhibitor that is utilized widely in experimental studies. According to the Morisco et al. study [41], using Wortmannin results in the suppression of Akt in both basal and ISO-stimulated states. However, ISO-stimulated ERKpp level is only reduced in response to Wortmannin [45]. These observations validate our model in which the PI3 K/Akt pathway is activated only through Giβγ:PI3K and on the other hand ERK pathway is activated through parallel mediators.

Fig. 11
figure 11

Effects of β-AR stimulation on ERK1/2 activity. a The experimental data for ERK1/2 pp after 8 min of ISO stimulation with and without PKA inhibition (H89) were obtained from Zou et al. study [69] for rat cardiac myocytes. Data represent mean ± SE of three individual experiments. b Normalized ERK1/2 activity as a function of isoproterenol concentration. The simulation result is indicated by a solid line and the experimental data for ERK1/2 pp after 5 min of ISO stimulation were obtained from Shenoy et al.’s study [55] for HEK-293 cells. Data represent mean ± SE of three individual experiments. c The time course of ERK1/2 pp after indicated ISO stimulation. The simulation result is indicated by a solid line and the experimental data were obtained from Bogoyevitch et al.’s study [7] for rat cardiac myocytes. Data represent mean ± SE of at least three independent experiments

Full size image

We also calculated the cellular ERKpp concentration after 5-min ISO stimulation with different concentrations to illustrate the ERK pathway sensitivity to β-adrenergic receptors agonist, see Fig. 11b. Our result is relatively close to the experimental data. Moreover, our model is calibrated to match the time course of ERK activation by 10 µM ISO, as seen from Fig. 2f. To validate the model results, the simulated time course of ERK activation by 50 µM ISO is compared with experimental results from rat cardiomyocytes, see Fig. 11c. The simulated ERK activity reaches its peak in 7 min (5 min in rat cardiomyocytes) after ISO stimulation and then reduces to its steady-state level in 1 h.

Dynamics of the transcription factors during β-ARs stimulation

ISO-induced activation of CREB occurs through phosphorylation by PKA and Akt and on the other hand GSK3β as a negative regulator inhibits that. We calibrated our model to fit the sensitivity of active CREB to isoproterenol in our model to the experimental data as shown in Fig. 2g. In the model, the calculated EC50 for active CREB is 56 nM, which is very close to the measured EC50 = 52.7 nM for the rat cardiomyocytes. Also, we calculated the variation of ISO-induced active CREB concentration (CREBp) to compare with the experimental data. As illustrated in Fig. 12a, the model could correctly predict the variation of active CREB after ISO stimulation from rat cardiomyocytes. To determine the contribution of β1-AR and β2-AR subtypes stimulation in CREB activation, we selectively inhibited β1-AR and β2-AR by 50 and 100%. As shown in Fig. 12b, inhibition of β1-AR by 50% decreases active CREB steady-state concentration to 62% of its value at physiological state and it is 68% for β2-AR inhibition. In the complete inhibition of β-ARs, steady-state concentration of active CREB reduces to 19% and 42% for β1-AR and β2-AR inhibition, respectively. Therefore, Fig. 12b shows that in addition to β1-AR, β2-AR also has a great effect on ISO-induced CREB activity and consequent cardiac hypertrophy. Also, in β1-AR selective inhibition by 50%, the time course of CREB activity is similar to physiological one with two peaks. The first and the second peaks originate from PKA and Akt/GSK3β activation, respectively (see also Fig. 12e). However, the time course of ISO-induced CREB activation after inhibition of β2-AR by 50% is different from β1-AR and has only the first peak, which is due to the decrease in Akt/GSK3β activity.

Fig. 12
figure 12

Effects of β-AR stimulation on CREB activity. a ISO-induced CREB activity. The experimental data were obtained from Shin et al.’s study [56] for rat cardiac myocytes after 5 min of indicated ISO stimulation. Data represent mean ± SE of at least three independent experiments. b Effects of β-AR subtypes on CREB activity. The time course of ISO-induced CREB activity in physiological (solid line), β1-AR inhibition by 50% (hollow circle) and 100% (filled circle), and β2-AR inhibition by 50% (hollow square) and 100% (filled square). c Effects of β1/ β2-AR ratio on CREB activity The ratios are 9:1, 8:2, 7:3, 6:4, and 5:5. d Simulated time course of CREB activity after ISO stimulation (0.01 µM dash-dotted line, 0.1 µM dashed line, and 1 µM solid line). e Effects of β-adrenergic mediators on CREB activity. The time course of ISO-induced CREB activity in physiological (solid line) and artificial states including blocking direct effect of PKA (triangle), and Aktpp (circle), and blocking ISO-induced variation in GSK3β (square)

Full size image

The ratio of β1/β2-AR is not constant for different species and also varies in cardiomyocytes through different cellular processes. Therefore, we investigated the influences of β1/β2-AR ratio variation on CREB activity. As is clear from Fig. 12c, decrease in the β1/β2-AR ratio (with constant total concentration of β-ARs) from 9:1 to 1:1 elevates CREB activity. This elevation indicates the significant role of β2-AR in activation of CREB and consequent cardiac hypertrophy by ISO. Also, the simulated time course of CREB activation after β-ARs stimulation by different ISO concentrations is displayed in Fig. 12d. The active CREB reaches its maximum within 20 min and then declines to its steady-state level in 2 h [56].

For CREB transcription factor, several mediators including PKA, Akt, and GSK3β have direct effects on its activity. In Fig. 12e, we analyzed each of these mediators’ contribution in CREB activation. After blocking the direct effect of PKA on CREB, the ISO-induced CREB activity reduces to 33% of its control value. For Aktpp and GSK3β, ISO-induced CREB activity reduces to 80 and 59% of its control value, respectively. Therefore, PKA is the main mediator for CREB activity and GSK3β plays the major role in PI3 K/Akt/GSK3β pathway for CREB activation and consequent cardiac hypertrophy. These results are in accordance with experimental observations in cardiomyocytes [12, 24]. Therefore, in addition to the known PKA, GSK3β is also an important potential candidate for treatment of the β-AR-induced cardiac hypertrophy.

While both classical and non-classical β-adrenergic pathways contribute directly to CREB activation, only non-classical pathway components induce GATA4 activation in our model. In this regard, we analyzed ISO-induced GATA4 activation through Ras/Raf/MEK/ERK and PI3K/Akt/GSK3β pathways. As seen in Fig. 2g, we constrained the GATA4 model parameters to replicate the time course of ISO-induced GATA4 activation from rat cardiac myocytes. To date, several studies have reported an increase in GATA4 transcriptional activity or mRNA level in response to ISO stimulation [35]. It is found that an increase in transcriptional activity or mRNA level of a transcription factor could lead to cardiac hypertrophy [8]. Due to the lack of experimental data on ISO-induced GATA4 transcriptional activity, we compared model results with data on the GATA4 mRNA level after ISO stimulation. According to the studies on cardiac myocytes, ISO stimulation increases the GATA4 mRNA level two- three-folds for 1 µM [65] and 10 µM [34] ISO and results in cardiac hypertrophy. We also predicted a twofold increase in the steady-state GATA4 activity after same ISO stimulation through the model. Hence, our model could predict the effects of ISO-induced GATA4 activation on cardiac hypertrophy with a close approximation to available experimental data.

Figure 13a illustrates the contribution of β1-AR and β2-AR stimulation on GATA4 activity. We repeated selective inhibition of β-ARs by 50 and 100% as mentioned before to simulate variations in GATA4 activity. In the physiological state, 1 µM ISO stimulation results in a 1.95-fold increase in GATA4 steady-state activity. Inhibition of β1-AR by 50 and 100% decreases the ISO-induced GATA4 activity to 1.4-fold and 1.1-fold, respectively. On the other hand, inhibition of β2-AR by 50% decreases the ISO-induced GATA4 activity to 1.21-fold of its basal value and inhibition of β2-AR by 100% results in the complete deactivation of active GATA4 in both basal and ISO-induced states. As is clear from Fig. 13a, β2-AR has a major role in ISO-induced GATA4 activation and consequent cardiac hypertrophy.

Fig. 13
figure 13

Effects of β-AR stimulation on GATA4 activity. a Effects of β-AR subtypes on GATA4 activity. The time course of ISO-induced GATA4 activity in the following states physiological (solid line), β1-AR inhibition by 50% (hollow circle) and 100% (filled circle), and β2-AR inhibition by 50% (hollow square). b Effects of β1/ β2-AR ratio on GATA4 activity. The ratios are 9:1, 8:2, 7:3, 6:4, and 5:5. c Effects of β-adrenergic mediators on GATA4 activity. The time course of ISO-induced GATA activity in the following states physiological (solid line), and artificial [blocking ISO-induced variation in GSK3β (square)]. d Simulated time course of GATA4 transcription factor after ISO stimulation for different concentrations (0.01 µM dash-dotted line, 0.1 µM dashed line, and 1 µM solid line)

Full size image

To analyze the effects of β1/β2-AR ratio variation on GATA4 activity, we changed the ratio from 9:1 to 1:1 as shown in Fig. 13b. The response of GATA4 activity to decrease in the ratio of β1/β2-AR is the same as CREB but due to the β2-AR’s major role in GATA4 activation, the resultant variation in GATA4 activity is larger than CREB. Also, to determine the contribution of ERK1/2-pp and GSK3β in ISO-induced GATA4 activity, we blocked the ISO-induced variation in GSK3β. As shown in Fig. 13c, without GSK3β contribution, the maximum and steady-state GATA4 activities are lower than physiological state and practically the effect of ERK1/2 pathway on GATA4 significantly decreases after 1 h. Therefore, as observed in experimental studies [42], GSK3β plays a significant role in GATA4 activation and consequent cardiac hypertrophy. The simulated time course of GATA4 activation after β-ARs stimulation by ISO is also displayed for 3 h in Fig. 13d. The active GATA4 time course is similar to CREB and rises to its maximum within 30 min and then reduces to its steady-state level in 2–3 h [42].

Mediators’ contribution to the hypertrophic response

After constructing our model and calibrating the unknown parameters, we performed a sensitivity analysis to determine the contribution of model parameters in the selected outputs. We chose steady-state activities of PKA, GSK3β, ERK1/2, GATA4, and CREB for our analysis due to the crucial roles of these variables in the cardiomyocyte response to hypertrophic stimulation. We derived the outputs local sensitivities to parameters perturbation \(\left( {\Delta p = 1.01p - 0.99p} \right)\) and normalized them to compare the parameters’ contribution to the outputs values. For this analysis, we set the isoproterenol concentration to 0.1 µM, which is a moderate agonist concentration to induce hypertrophy in cardiomyocytes [66]. The resultant graph of normalized output sensitivities is illustrated in Fig. 14. We also obtained a similar result by performing this analysis with \(\Delta p = 1.05p - 0.95p\).

Fig. 14
figure 14

Contribution of model parameters in mediating hypertrophic response. Each column represents the sensitivity of the outputs (+1 maximum activation and −1 maximum inhibition) to the perturbation in indicated parameter. The associated parameter of each number is shown in Table S10 (supplementary materials)

Full size image

We calculated the sensitivities for all of our model parameters. The list of model parameters and their associated numbers is shown in Table S10 (see supplementary materials). The top five parameters with highest and lowest scores for each of the selected outputs are listed in Table 1.

Table 1 Highest and lowest scored parameters in β-adrenergic pathway sensitivity analysis
Full size table

According to Table 1, for the CREB transcription activity, Akt and AC play the major roles. Akt activation enhances the CREB activity by two methods: (1) reducing the inhibitory effect of GSK3β on the CREB, and (2) activating CREB by its phosphorylation. The AC activation influences the CREB activity by activating PKA catalytic subunits and subsequent CREB phosphorylation. Also, higher expression of CREB transcription factor enhances ISO-induced cardiac hypertrophy through CREB. On the other hand, an increase in the hill coefficient of AC activation by Gsα reduces the cAMP level by attenuating its production and elevated concentration of PDEs leads to the same result by amplifying cAMP degradation. Finally, the diminished cAMP level results in a decrease in PKA and CREB activity. PP2A also inhibits the CREB activity by dephosphorylation of Akt-pp and reducing its effect on CREB activation.

As seen from Table 1, the most effective parameters for the GATA4 transcriptional activity and ERK activity are the same. This is due to the dominant effects of ERK activity on GATA4 activation. The kinetic parameters that regulate Src, Shc, and Ras activation play the main roles in GATA4 activation. Also, an increase in the Grb2 and Akt total concentration activates and inhibits GATA4 activation, respectively. Elevated Grb2 enhances ERK activity, and on the other hand an increase in the Akt concentration inhibits ERK activity by Raf deactivation. The Akt activation acts as a double-edged sword in ISO-induced cardiac hypertrophy due to its effects on CREB and GATA4 activation. This effect emerges from considering the interrelations between PI3 K/Akt and Ras/Raf/MEK/ERK pathways, which will be missed if researchers only study isolated pathways. Hence, it is critical to perform more experimental studies on the interrelations between β-adrenergic non-classical pathways to examine their effects on the cell response after hypertrophic stimulation.

Conclusions

In this study, a computational approach has been used to investigate the hypertrophic response of cardiac myocytes to β-adrenergic receptor stimulation. We considered the contribution of both β-adrenergic classical and non-classical signaling pathways in the regulation of hypertrophic transcription factors CREB and GATA4. There exist other transcription factors, such as NFAT, which contribute to β-AR-induced cardiac hypertrophy, but their activation depends mostly on the β-AR-induced Ca2+ variations, these will be presented in our future study. The current model was formulated by a system of ordinary differential equations and its parameters were obtained directly or estimated from experimental studies. We validated the model with an extensive range of experimental data. Our results indicated that, despite the low portion of β2-AR out of the total cardiac β-ARs (below 20%) in healthy cardiomyocytes, its contribution in inducing cardiac hypertrophy is noticeable. This contribution arises from its specific non-classical signaling through PI3K/Akt and Ras/Raf/MEK/ERK pathways. According to our result, GSK3β plays a significant role in ISO-induced CREB and GATA4 activation and blocking its modulation by ISO greatly diminishes the cardiac hypertrophy. Finally, we determined the β-adrenergic signaling mediators’ contribution to cardiomyocyte hypertrophic response through classical and non-classical pathways by performing a sensitivity analysis and realized that Akt activation has a double-edged-sword effect on cardiac hypertrophy.