1 Introduction

The continuous growth of artificial objects resident in near-Earth orbits is raising concerns among the experts (e.g., [1]), especially considering the recent proposals and deployment of LEO (low Earth orbit) large constellations [2,3,4,5,6]. International guidelines [7] recommend deorbiting all new satellites within 25 years since their end of operative life, if their orbital altitude is below 2000 km (in the LEO region), regardless of their dimension, mass, and orbit shape. This recommendation is currently leading all major spacecraft providers to install disposal systems on board their vehicles, to save propellant for deorbiting, or to arrange dedicated interfaces for on-orbit servicing and deorbit operations at the end of life. Among the proposed solutions, ElectroDynamic Tethers (EDTs) appear to be a promising option as they overcome the limitations of traditional chemical and electric propulsion (e.g., propellant leakages or degradations due to long storage time on board and attitude control demands) and are more effective than alternative passive devices [8]. Moreover, as highly encouraged by 2017 IADC guidelines [9], EDTs retain the ability to conduct collision avoidance maneuvers during the disposal phase. In fact, there is the possibility to modulate the current, and therefore the drag force, to vary the deorbiting performance when necessary. In this context, in 2018, the European Commission awarded an H2020 FET OPEN project with the title “Electrodynamic Tether Technology for Passive Consumable-less Deorbit Kit” (E.T.PACK), which aims at the development of a Deorbit Kit (DK) based on electrodynamic tether technology with TRL 4 [10,11,12].

1.1 Electrodynamic tethers deployment

Electrodynamic tethers were first proposed in the early 1970s [13, 14], and the first space experiments flew on board the Space Shuttle in the 1990s (TSS-1 and its re-flight TSS1-R) to demonstrate the feasibility of deploying long tethers and to conduct experiments in space plasma physics [15]. While collecting good results regarding the current level, experiments confirmed the complexity of tether deployment [16]. Several in-space [17, 18] and ground verifications [19,20,21,22], as well as theoretical investigations [23,24,25], followed the TSS missions. A demonstration flight (ProSEDS [26]) was prepared and qualified by NASA for flight in 2003, but it was canceled following the Shuttle Columbia accident. A recent project in Europe (BETs [27]) introduced the use of tape tethers instead of round wires due to their higher survivability to space debris impacts and better electrodynamic performance due to the larger perimeter for equal tether length and mass [28]. In late 2019, the TEPCE technology demonstrator [29] deployed a \(500-m\) EDT in a 300 km \(\times\) 860 km orbit. Despite the short deployed length and no detailed evidence about its on-orbit nominal deployment, the 3U Cubesat deorbited in about two months from its delivery orbit. In fact, it is clear that while the physics at the basis of tethered systems in space is well-known, the deployment of a space tether is still a critical issue in space tether missions. Specifically, in the TSS-1 experiment, the deployment failed due to a blockage in the tether leveling system of the deployer [30], and in the ESA YES2 mission the tether deployment was off-nominal [31, 32] because of the failure of a sensor. SEDS-I [33] and SEDS-II [34] were successful in deploying 20-km long tethers in space: the former one in 1993 with a high-amplitude libration necessary for the release of the capsule at the tether tip and the latter one in 1994 with the tether aligned along the local vertical (LV) at the end of the deployment.

Further improvements, both on the deployer technology [35] and deployment strategies [36], have been proposed to control tether deployment better and to avoid instabilities during the deorbit phase. Deorbiting missions must follow a deployment profile in terms of length and velocity versus time, bringing the system to a small libration amplitude at the end of the maneuver [34, 36]. In this paper, the proposed approach is further developed and applied to the E.T.PACK scenario. The objective is the clear definition of a strategy for deploying EDTs through a stable and well-defined trajectory, thus limiting libration oscillations at the end of the maneuver. Therefore, a reference profile is computed through an optimization process for the Deployment Mechanism (DM) to make the tethered system reach the desired final conditions. This reference profile also determines the design requirements of the E.T.PACK deployer sensing and motor subsystems.

1.2 Paper outline

The work presented in this manuscript is organized as follows. Section 2 introduces the E.T.PACK Deorbit Kit, focusing on its design drivers and the past mission approaches for the tether deployment. Section 3 introduces the mission requirements (e.g., deorbit time, operational desiderata, mass and volume constraints). Section 4 focuses on the deployment trajectories, on the reference profiles for deployment and the definition of the deployer subsystems design requirements, and introduces future developments. Finally, Sect. 5 draws the relevant conclusions.

2 E.T.PACK Deorbit Kit

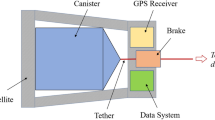
In this section, the E.T.PACK Deorbit Kit's main characteristics are introduced. The kit will be mounted on a host spacecraft, and after the end of its life, it will stabilize the satellite before deploying the EDT. EDTs collect ionospheric electrons passively from the plasma environment and re-emit them through a cathode (C-EDTs [37]) or a “low work-function” segment of the same tether by using thermionic and photoelectric effects (LWTs [38, 39]). In both cases, the resulting electric current flowing through the conductive tether generates a drag Lorentz force thanks to the interaction with the Earth’s magnetic field that progressively decreases the orbital altitude of the satellite, causing its re-entry in the atmosphere. The working principle of C-EDTs and LWTs is shown in the diagrams of Fig. 1. A sketch of the Deorbit Kit can be seen in Fig. 2. The Deorbit Kit proposed for the E.T.PACK project includes all the elements reported in the figure and can be divided into three different parts: the interface with the host S/C, the tether, and the tip mass; in the current configuration, the tip mass corresponds to the DM and includes all the subsystems necessary to perform the tether deployment.

A market analysis has been performed, identifying several attractive commercial scenarios to apply the Deorbit Kit. Among them, the most promising reference missions have been identified as:

  • De-orbit EO (Earth Observation) satellites in orbit at about 800 km altitude and 98\(^\circ\) inclination. Typical mass values of these spacecraft are between 700 and 1000 kg.

  • Deorbit small telecommunication satellites from 1200 km altitude at 90\(^\circ\) inclination. The typical mass of large constellation spacecraft is in the order of 200–300 kg.

This market analysis revealed that a multi-km tape tether should be used for the EO S/C. Further details on the Deorbit Kit and on the expected operations modes (e.g., hibernation, S/C stabilization, deployment) for the mentioned reference missions can be found in [12]. Accordingly, few issues directly affect design decisions about the DM:

  • the DM should host a tape with typical dimensions of a few km of length, with a cross-section of a few cm in width by tens of microns in thickness;

  • the DM should also be able to handle tapes of different thicknesses, which is the case of the LWT will be coated;

  • the longitudinal structure of the tether is complex, and it involves an inert segment necessary for dynamic stabilization, a bare aluminum tether for capturing electrons, with an insulated segment near the cathode;

  • the amplitude of the tether oscillations about the local vertical at the end of the deployment should be below a threshold (e.g., 10\(^\circ\)).

The design drivers for the DM are:

  • to have a simple design;

  • to provide good operability;

  • to minimize sensitivity to environmental/external loads;

  • to provide the required performance with minimum mass, minimum volume, simple interfaces, and low cost;

  • to host tapes of different thicknesses and different tribological properties (in particular, tethers coated with Low Work-Function materials);

  • to be able to control the deployment profile.

Based on the criteria mentioned above, a trade-off analysis was focused on the DM and on the entire system, giving particular attention to the deployer technology and the ejection technique.

The ejection technique adopted for starting the deployment is a crucial issue. Deploying a few-kilometers-long tether requires keeping the tether tension very low once the initial velocity is reached, and the deployment is then driven by the acquired linear momentum with very little help from the gravity gradient in the early stages of deployment. This issue has proved to be critical, and it may be solved by keeping the friction low enough by employing an active system to extract the tape from the spool. Deploying a tape requires using a low-acceleration system to reach the desired separation velocity in the initial stage of deployment. After a thorough comparison of the advantages and shortcomings of both configurations, we chose an in-line cold gas thrust system over a long-stroke push-boom system.

Fig. 1
figure 1

Working principle of (top) C-EDT and (bottom) LWT System in retrograde orbit (e.g., sunsynchronous)

Full size image
Fig. 2
figure 2

Basic deployer kit configuration with the interface to the satellite (top), the tape tether and the DM (bottom)

Full size image

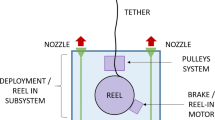
The basic DM configuration consists of:

  • Reel;

  • Pulley assembly, consisting of motorized guiding pulleys;

  • Cold gas system, required for attaining the desired velocity in the early phase of deployment;

  • Battery ;

  • Drivers and electronics;

  • Onboard computer;

  • Sensors and data handling.

The deployer technology that was adopted in the past missions falls into three basic categories:

  • Rotating reels (e.g., [16]);

  • Stationary spools (e.g., [32, 33]);

  • Folded/pleated tethers (origami) (e.g., [40]).

The folded solution is not compact enough and not suited for a kilometer-long tether made of metal or plastic (e.g., Kapton) that retains a memory of sharp turns. Consequently, the baseline designs of concepts for the DM involving either a rotating reel or a stationary spool have been investigated (see Fig. 3). The technology of rotating reels is well-known and is commonly used to store and deploy long ropes, cables, and tapes (e.g., [16, 36, 41, 42]). This technique works independently of the cross-sectional shape of the element being deployed, requiring only suitable modifications of the DM. Stationary spools are also commonly used for lighter ropes or threads. Deploying from a stationary spool implies that the exiting tether acquires a 360\(^\circ\) torsional rotation per deployed turn, that is, several thousand turns for a tether that is kilometer long. Thus, the reeling technology fits more readily with a tape-shaped tether, but the stationary spool has its own advantages over it (e.g. smaller size, no reel support, and bearings). Both solutions were considered in the trade-off analysis with the selection of the stationary spool for a first E.T.PACK demonstration breadboard.

Fig. 3
figure 3

Schematics of stationary spool (top) and rotating reel (bottom) configurations for the tape deployer

Full size image

3 Requirements definitions

The main requirements that have driven the design of the DM proposed for E.T.PACK are based on the Deorbit Kit requirements generated by the E.T.PACK team during the first phase of the project to fulfill ESA requirements at system level and are included in the H2020 proposal to the EU [10]. The target requirements specified for the DM are summarized in Table 1.

Table 1 DM target requirements
Full size table

The selection of the tether geometry is another key issue in tether mission design. Only five missions deployed tethers in space that were several kilometers long, and they all involved cylindrical tethers. However, being a considerable technological improvement, tape-shaped tethers have been selected for the E.T.PACK Project, and length L, width w, and thickness h have been sized considering a combination of

  • electrodynamic performance during deorbit;

  • survivability to micro-meteoroids and orbital debris impacts;

  • ability to collect electrons (i.e., anodic effectiveness);

  • and dynamic considerations.

A more extensive description of the advantages of tape tethers with respect to cylindrical ones is reported in [46,47,48].

A key requirement that drives the design of the deployer is whether the tethered system needs to be deployed only once or it needs to be retrieved. E.T.PACK requires a 3-km-long system to be deployed once (no retrieval) and utilizes a ribbon-shaped tether/tape. A system deployed while in orbit without any specific control will end up with a very large libration amplitude of the system with respect to the LV. An EDT is continually perturbed by a varying Lorentz force during deorbit, and consequently, it will not stay aligned with the LV, but rather it will oscillate about it both in the orbital and out of the orbital planes [49]. The amplitudes of the oscillations will result from the relative geometry between the tether and the magnetic field. The out of plane component is particularly significant at high orbital inclinations. The libration amplitude remains stable in the absence of perturbing forces but, if the amplitude starts at a large value, it will take a small number of perturbing cycles to become unstable and turn the system upside-down or vice versa. Specifically, above an amplitude of 45\(^\circ\), the restoring torque, provided by the gravity gradient, decreases with the amplitude making it less and less effective. Above a value of about 65\(^\circ\), the tether loses tension [44] during parts of the libration cycle, a condition that is not desirable from the overall stability point of view. As dynamic simulations showed, a longitudinal damper (in series with the tether) is an effective way to damp the tether oscillations produced by Lorentz forces during deorbit [45]. Consequently, for an EDT system, it is desirable to start the deorbiting operations with a limited oscillation amplitude to have favorable initial conditions. Furthermore, in order to avoid a more complicated system that needs to perform a phased yo-yo sequence for canceling the libration associated with an uncontrolled deployment, it is preferable to derive a deployment profile that provides a libration with a small amplitude at the end of the maneuver. Additionally, environmental requirements for the Deorbit Kit, and consequently the DM, must be added to guarantee functionality in the operating environment from start to end. Table 2 specifies preliminary launch load requirements for the kit essential in comparing alternative designs of the DM. The static launch envelopes and the PSD (Power Spectral Density) of the random vibration launch load, which refers to a typical rocket delivering payloads launched to LEO, can be found in Ref. [50].

Table 2 Launch load requirement
Full size table

4 Deployment dynamics

The deployment of the system starts with an initial velocity that could be imparted either over a very short time (e.g., by compressed springs) or over a relatively long time at a smaller acceleration (e.g., a long deployable boom or an in-line thruster system, the latter being the solution chosen in E.T.PACK). Generally speaking, it is desirable to start deployment with a small initial velocity for reasons such as (a) the librational stability of the system and (b) reducing the size and mass of the ejection system.

Once the system is accelerated to the initial velocity, it will continue to deploy under its initial momentum if the tether is not dragged, and with greater and greater help from the gravity gradient pulling on the tip mass as the tether length increases.

The deployment dynamics is non-linear. The general tendency, due primarily to the Coriolis accelerations acting on the tip mass, is to end up with libration amplitudes that are typically in the range 40\(^\circ\)–50\(^\circ\) [44]. The first step is, therefore, to derive length and velocity profiles vs time that, for given initial conditions, bring the system from those initial conditions to a small libration amplitude at the end of the maneuver.

4.1 Mathematical model

The reference profiles of length and length rate vs. time provide the “trajectory” in phase space that the tip mass must follow for reaching the desired final dynamic state (e.g., small libration amplitude and small longitudinal velocity) starting from given initial conditions. The equations of motion of a variable-length tether orbiting system are strongly non-linear and with time-varying coefficients. A linearized analysis can only provide useful information under the assumptions of small angles and a constant tether length, and hence it does not apply to deployment. For this reason, the  numerical optimization of the deployment maneuver was carried out by solving a boundary value problem of the non-linear dynamic system to find the trajectory in phase space that the tether must follow to reach the final state. The reference profiles will be used by the DM to make the tethered system reach the desired final conditions. The reference profiles are also important for determining the requirements of the sensing and motor systems of a specific deployer design to be able to implement them.

The reference frame utilized for the deployment dynamics is an orbiting reference frame (see Fig. 4) rotating at constant angular velocity \(\omega _0\) in which the origin G is placed at the center of mass (CoM) of the entire tethered system, \(\theta\) and \(\phi\) are the in-plane angle and out-of-plane angle of libration, respectively.

Fig. 4
figure 4

Orbiting reference frame

Full size image

The model adopted for the analysis of the deployment dynamics is a classical dumbbell model with a straight and inelastic tether of variable length that takes into account the mass flow of the tether [36]. From the 3-D equations of motion, it can be noted that if the system is deployed on the orbital plane (i.e., with \(\phi = 0\)), then the in-plane motion does not excite the out-of-plane motion and the dynamics reduces to a 2-D scenario, governed by the variables l and \(\theta\). The effects of out-of-plane errors at release and those associated with the tether flexibility are addressed in the following subsections. The 2D dumbbell model system is well justified for deriving the reference profile. This model has provided a very good agreement in the past missions of SEDS-I [33] and SEDS-II [34] between the pre-flight deployment simulations and the flight data.

To obtain the 2-D equations of motion for the deployment maneuver, we used a Lagrangian approach also considering that the tape-shaped tether is stored on board the tip-mass and released from it, and adopting the tether length l(t) and the in-plane libration angle \(\theta (t)\) as generalized variables (Fig. 5). The in-plane libration angle can also be expressed as the supplementary of \(\theta _\mathrm{nadir}\), the in-plane angle from the nadir direction. In addition, since the mass of the host spacecraft is much higher than that of the tip-mass (\(m_\mathrm{TM}<<m_\mathrm{sc}\)), we assumed that the origin of the orbiting reference frame is coincident with the CoM of the host spacecraft. The resulting 2-D equations of motion are [36]:

$$\begin{aligned} \ddot{l}= & {} \frac{2\,F_\mathrm{thr}-2\,T_\mathrm{p}+\rho _\mathrm{l} \,{\dot{l}}^2}{2\,m_0-2\,\rho _\mathrm{l}\,l} + l\,(2\,{\dot{\theta }}\,\omega _0+{\dot{\theta }}^2+3\,\omega _0^2\,\cos ^2\theta ) \end{aligned}$$
(1)
$$\begin{aligned} \ddot{\theta }= & {} 6\,{\dot{l}}\, \frac{(m_0-\rho _l\, l)({\dot{\theta }}+\omega _0)}{l\,(-3\,m_0+2\rho _\mathrm{l}\,l)} -3\,\omega _0^2\,\cos ^2\theta \, \sin \theta \end{aligned}$$
(2)

where \(m_0=m_\mathrm{TM}\) \((t=0)\) is the initial mass of the tip-mass including the total mass of the tether, \(\rho _\mathrm{l}\) the linear density of the tether, \(F_\mathrm{thr}\) the force applied to the tip-mass and along the tether direction by the thruster system on board the tip-mass and \(T_\mathrm{p}\) is the tether tension at the exit of the tip-mass, respectively.

Fig. 5
figure 5

Mathematical model of the 2-D deployment dynamics

Full size image

4.2 Deployment reference profiles

The reference profiles for the deployment maneuver were obtained using the BOCOP software [51] that approximates the optimal control problem by a finite-dimensional optimization problem (NLP) using a time discretization. The NLP problem is then solved by the software Ipopt (based on interior point optimization), using sparse exact derivatives computed by ADOL-C [51].

Considering \(x(t)=[\,l,\theta ,{\dot{l}},{\dot{\theta }}\,](t)\) as state variable and \(u(t)=T_\mathrm{p} (t)\) as the input variable, the objective is to find the dynamic state trajectory x(t) and the input variable trajectory u(t) for \(t\in [\,0 ,t_\mathrm{f} ]\) that minimize the following cost function:

$$\begin{aligned} J(\theta _\mathrm{f},{\dot{\theta }}_\mathrm{f} )=(\theta _\mathrm{f,ref}-\theta _f )^2+k\, ({\dot{\theta }}_\mathrm{f,ref}-{\dot{\theta }}_\mathrm{f} )^2 \end{aligned}$$
(3)

with \(\theta _\mathrm{f,ref}=\pi\), \({\dot{\theta }}_\mathrm{f,ref}=0\), \(k=10\), and subject to the following constraints:

  • dynamics: the dynamics is given by Eqs. 1–2;

  • boundary conditions:

    • \(l_0=0.5\) m;

    • \(\theta _0 \in [3.2, 3.6]\) rad, i.e., \(\theta _0 \in [185, 205]\) deg;

    • \({\dot{l}}_0=0\) m/s;

    • \({\dot{\theta }}_0=0\) rad/s;

    • \(l_f=3000\) m;

    • \({\dot{l}}_f=0\) m/s;

  • other constraints:

    • \(t_f= 3600\) s;

    • \(l\in [0 ,3000]\) m;

    • \(\theta \in [2.3 ,4.6]\) rad;

    • \({\dot{l}} \in [0 ,1.4]\) m/s;

    • \({\dot{\theta }}= [-0.0015 ,0.0015]\) rad/s;

We adopted \(k = 10\) to compensate for the smaller value of the libration rate error at the end of deployment with respect to the final libration angle error. The condition on \(\theta _0\) can be equivalently expressed as \(\theta _\mathrm{nadir,0} \in [5, 25]\) deg.

The selected final time \(t_\mathrm{f}\) is a trade-off solution between the two following points. A shorter final time implies that the deployment maneuver has to be completed in a shorter time interval, and consequently, the length rate assumes higher values on average, especially at the beginning (initial acceleration phase) and at the end (final deceleration phase) of the deployment. Conversely, a longer time for deployment to take place requires a lower length rate on average, leading to a too-small length rate near the cusp (at time \(t=1500\) s for ID = 5 in Fig. 9), which is an undesirable condition.

The constraints on each state variable were selected considering our previous experience in this subject to limit the discretization intervals for each state variable and guarantee the convergence of the optimization algorithm.

Table 3 Release angle values for each scenario ID
Full size table

As mentioned earlier, the reference profiles depend strongly on the initial conditions. The deployment trajectories were analyzed considering different values of the release angle referred to nadir direction \(\theta _\mathrm{nadir,0}\) from 5\(^\circ\) to 25\(^\circ\), according to the scenario ID listed in Table 3.

Fig. 6
figure 6

Deployment trajectory of the tip mass in the orbital plane of the host spacecraft for different values of the release angles \(\theta _\mathrm{nadir,0}\) (see Table 3)

Full size image
Fig. 7
figure 7

Deployment trajectory of the tip mass in the orbital plane with a lumped mass discretization of the tether underlining the negligible effect of flexibility during the deployment (\(\Delta l = 250\, m\), snapshots at \(\Delta t = 400\) s)

Full size image
Fig. 8
figure 8

Time profiles of the tether length l(t) for different values of the release angles \(\theta _\mathrm{nadir,0}\) (see Table 3)

Full size image
Fig. 9
figure 9

Time profiles of the tether length rate \({\dot{l}}(t)\) for different values of the release angles \(\theta _\mathrm{nadir,0}\) (see Table 3)

Full size image
Fig. 10
figure 10

Time profiles of the tether length rate \({\dot{l}}(t)\) for the first 100 s (top) and the last 100 s (bottom) of the deployment for different values of the release angles \(\theta _\mathrm{nadir,0}\) (see Table 3)

Full size image
Fig. 11
figure 11

Time profiles of the in-plane libration angle referred to nadir direction \(\theta _\mathrm{nadir}(t)\) for different values of the release angles \(\theta _\mathrm{nadir,0}\) (see Table 3)

Full size image
Fig. 12
figure 12

Time profiles of the in-plane libration rate referred to nadir direction \({\dot{\theta }}_\mathrm{nadir}(t)\) for different values of the release angles \(\theta _\mathrm{nadir,0}\) (see Table 3)

Full size image
Fig. 13
figure 13

Time profile of the tether tension \(T_p (t)\) for different values of the release angles \(\theta _\mathrm{nadir,0}\) (see Table 3)

Full size image

The simulation results are shown in Figs. 6, 7, 8, 9, 10, 11, 12 and 13. Figure 6 depicts the 2-D deployment trajectory of the tip mass in the orbital plane of the host spacecraft for the different values of the release angle. This figure shows that the deployment trajectory consists of an initial curved part that includes the acceleration phase provided by the thruster system on board the tip-mass, a “cusp” at which the libration angle reaches its maximum value, and a final portion in which the tip-mass moves toward the local vertical.

An additional set of simulations with a lumped mass discretization of the tether has been performed with the aim of highlighting the evolution of the shape of the tether as the tip mass progresses. Figure 7 shows that tether bending is rather limited, as expected since the tether is maintained taut during the deployment. Moreover, neglecting the environmental forces during deployment is well justified because: (a) aerodynamic drag is negligible at the considered altitude; (b) the effects of solar radiation pressure over the deployment time are negligible, and (c) the Lorentz force is null during deployment because the cathode is switched off. Consequently, the model adopted for deriving the reference profile is a good representative of the key effects during deployment.

Figures 8 and 9 show the evolution of the tether length l(t) and length rate \({\dot{l}}(t)\), respectively, i.e., the reference profiles to be followed by the tip-mass and controlled by the motor driving the pulley assembly that extracts the tape from the DM. As also detailed in Fig. 10, the length rate profile \({\dot{l}}(t)\) consists of a first linear portion due to the thruster system acceleration, at the end of which the length rate reaches the maximum value of about 1.4 m/s. Toward the end of the deployment, the length rate \({\dot{l}}(t)\) shows a final deceleration phase going from 1.2–1.3 to 0 m/s.

Figures 11 and 12 show, respectively, the resulting time profiles of the in-plane libration angle referred to nadir direction \(\theta _\mathrm{nadir}(t)\) and its rate \({\dot{\theta }}_\mathrm{nadir}(t)\). If \(\theta (t)_\mathrm{nadir}\) and \({\dot{\theta }}_\mathrm{nadir}(t)\) profiles are followed by the tip-mass controlled by the DM, they provide a final libration amplitude close to zero, in good accordance with the required value of \(< 10^\circ\), and a final velocity that approaches zero at a tether length that approaches 3000 m. The final longitudinal velocity is an easier requirement to meet than the libration amplitude, and small adjustments to the final phase of deployment can be easily implemented in the control system to stop the deployment at the required tether length.

Previous figures show that if the release angle referred to nadir direction \(\theta _\mathrm{nadir}\) is too low, i.e., \(|\theta _\mathrm{nadir}| = 5^\circ\), corresponding to the dashed orange curves in the figures, the tip-mass moves away from the local vertical direction before reaching a cusp and progressively comes back to the local vertical attaining an angular velocity close to zero at the end of the deployment trajectory. In addition, the time profile of \(\,{\dot{l}}(t)\) shows an evident oscillation with respect to the more regular curve of scenario with ID = 3 and the time profile of \(T_p(t)\) shows an oscillation in the time interval [500,1500] s that includes the cusp (see Fig. 13). On the other hand, if the release angle \(\theta _\mathrm{nadir}\) is too high, i.e., \(|\theta _\mathrm{nadir}| = 25^\circ\), corresponding to the continuous green curves in the figures, the time profile of \(\,{\dot{l}}(t)\) starts oscillating with respect to the more regular curve of scenario 3 and the magnitude of the libration rate \({\dot{\theta }}_\mathrm{nadir}\) reaches higher values than for the other scenarios.

Regarding the in-line thruster, a constant thrust is needed to guarantee that the tether remains in tension in the early stage of the deployment when the contribution of gravity gradient forces is very low (due to the very low tether length). The level of the thrust does not need to be very accurate because the deployment is controlled in velocity by the driving pulleys of the deployer that follow the velocity reference profile. A higher thrust level would only produce a higher tether tension (when the thruster is activated) without changing the velocity profile.

The previous analysis shows that a valid choice for initial conditions appears to be \(\theta _\mathrm{nadir,0}=0.262\) rad \(=15^\circ\) for a cold-gas thrusting force \(F_\mathrm{thr}=0.4\) N acting for the first 64 s of the deployment maneuver. These conditions provide enough linear momentum to the tip mass, a stable deployment (i.e., the system does not tip over), and allow a design with a reasonably light ejection system.

The following considerations refer to the scenario with ID = 3 for the sake of clarity, without any loss of generality. After the tether has been completely deployed, the tethered system is almost aligned with the local vertical, i.e., \(\theta _\mathrm{nadir}=0^\circ\), and the tension the tether experiences can be computed from Equation 1 imposing \(\ddot{l}=0\) m/s\(^2\), \({\dot{l}}=0\) m/s, \(l=l_\mathrm{tot}=3\) km, \({\dot{\theta }}=0\) rad/s and \(\theta =\pi\):

$$\begin{aligned} T_\mathrm{p,ref} = 3\,(m_0-\rho _l\,l_\mathrm{tot})\,\omega _0^2\,l_\mathrm{tot}= 93.8\,\mathrm{mN} \end{aligned}$$
(4)

\(T_\mathrm{p,ref}\) is almost five times lower than the tether tension peak at the end of the deployment, i.e., \(\simeq 541.2\) mN, causing a bounce of the tether that is undesirable (Fig. 14). The final tether tension peak is due to \(\ddot{l}\) that is not equal to zero at the end of the deployment (it can be seen from the slope of the curve in the bottom panel in Fig. 10 and from Eq. 1). To solve this issue, the final part of the length rate profile was modified by imposing the following “half-cosine” profile starting from time \(t_i\) (see the top right panel of Fig. 15):

$$\begin{aligned} {\dot{l}}^*(t)= \frac{{\dot{l}}_i}{2}\left[ cos\left( \pi \frac{t-t_i}{t_f^*-t_i}\right) +1\right] \end{aligned}$$
(5)

where \(t_i=3487.5\) s is the time instant corresponding to a local maximum of the original \({\dot{l}}(t)\) profile (the densely dotted blue curve in Fig. 15), \({\dot{l}}_i={\dot{l}}(t_i)\), and \(t_f^*=3673.7\) s is the new final time of the deployment maneuver, computed by imposing that the tether is completely deployed when the new \({\dot{l}}^*(t)\) profile is imposed. The resulting new profiles of \(\ddot{l}^*(t)\) and \({l}^*(t)\) can be obtained by computing the time derivative and the integral of \({\dot{l}}^*(t)\), respectively, whereas the new time profiles of \(T_\mathrm{p}^*(t)\) (see Fig. 14) for the final part of the deployment and of \(\theta ^*_\mathrm{nadir}(t)\), \({\dot{\theta }}^*_\mathrm{nadir}(t)\) (see Fig. 15) are computed from Eqs. 1 and 2 by imposing the new final profiles \(l^*(t)\), \({\dot{l}}^*(t)\) and \(\ddot{l}^*(t)\).

Fig. 14
figure 14

Time profiles of (densely dotted blue line) tether tension \(T_\mathrm{p}(t)\) provided by the optimization process with the final peak; (solid red line) tether tension \(T_\mathrm{p}^*(t)\) obtained with the new smooth final deceleration profile; and (dashed green line) the steady-state value of the tether tension at the end of the deployment \(T_\mathrm{p,ref}\)

Full size image
Fig. 15
figure 15

Time profiles of the tether length l(t) (upper left panel), length rate \({\dot{l}}(t)\) (upper right panel), libration angle \(\theta _\mathrm{nadir}(t)\) (lower left panel) and libration rate \({\dot{\theta }}_\mathrm{nadir}(t)\) (lower right panel) at the end of the deployment referred to the sudden final deceleration (dashed blue line) and to the smoother deceleration (solid red line). The red dot refers to the time instant \(t_i\)

Full size image

4.3 Sensitivity analysis to release angle errors

Additional sets of simulations have been performed to evaluate the influence of release angle errors, both in-plane and out-of-plane.

Figure 16 shows the deployment trajectories obtained considering different errors of the in-plane release angle \(\epsilon _{\theta _\mathrm{nadir,0}}\) with respect to the same reference profile trajectory to follow: in all cases, the deviation from the nominal trajectory is limited. The evolution of the in-plane libration angle referred to nadir direction \(\theta _\mathrm{nadir}\) is highlighted in Fig. 17.

Fig. 16
figure 16

Deployment trajectories of the tip mass for different errors \(\epsilon _{\theta _\mathrm{nadir,0}}\) of the in-plane release angle \(\theta _\mathrm{nadir,0}\) with respect to the same reference trajectory (solid black line)

Full size image
Fig. 17
figure 17

Time profiles of the in-plane libration angle referred to nadir direction \(\theta _\mathrm{nadir} (t)\) for different values of error on the in-plane release angle \(\epsilon _{\theta _\mathrm{nadir,0}}\)

Full size image

The sensitivity of the out-of-plane deployment dynamics to initial out-of-plane release angle errors can be readily investigated by substituting the 2D model equations with the following equation system adapted from [52]:

$$\begin{aligned} \ddot{l}= & {} \frac{2\,F_\mathrm{thr}-2\,T_\mathrm{P}+\rho _\mathrm{l} \,{\dot{l}}^2}{2\,m_0-2\,\rho _\mathrm{l}\,l} + l\,\nonumber \\&\times \left[ ({\dot{\theta }}+\omega _0)^2\,\cos ^2\phi +{\dot{\phi }}^2-\omega _0^2+3\,\omega _0^2\, \cos ^2\theta \, \cos ^2\phi \right] \nonumber \\ \ddot{\theta }= & {} 2\, \left( \frac{{\dot{l}}}{l}\frac{3\,(m_0-\rho _\mathrm{l}\, l)}{(-3\,m_0 +2\rho _l\,l)} \,-{\dot{\phi }}\,\tan \phi \right) \, ({\dot{\theta }}+\omega _0)\nonumber \\&-3\,\omega _0^2\,\cos ^2\theta \, \sin \theta \nonumber \\ \ddot{\phi }= & {} -2\,m_R\frac{{\dot{l}}}{l}{\dot{\phi }}\nonumber \\&-\left[ ({\dot{\theta }}+\omega _0)^2+3\,\omega _0^2\,cos^2\theta \right] sin\phi \, cos\phi \end{aligned}$$
(6)

where \(m_\mathrm{R}\) is the reduced mass of the system and \(\phi\) is the out-of-plane libration angle. Equations 6 show that the coupling between the in-plane dynamics and the out-of-plane dynamics is of second order in the out-of-plane variable. Consequently, the out-of-plane dynamics can be investigated separately from the in-plane dynamics for small out-of-plane angles, and it does affect the in-plane dynamics appreciably. Figure 18 shows the out-of-plane libration angle and angular velocity for initial out-of-plane errors at release within 5\(^\circ\) that is the pointing accuracy planned for the E.T.PACK Deorbit Kit. As shown in Fig. 18, the effect of an out-plane error at release on the final libration amplitude is small.

Finally, Fig. 19 summarizes the results on post-deployment libration amplitude, both in-plane and out-of-plane, considering different values of errors on the release angles \(\phi _0\) and \(\theta _\mathrm{nadir,0}\). After the deployment, the tether oscillates around the nadir direction with a maximum amplitude smaller than \(1.5^\circ\) both in-plane and out-of-plane, for all the simulated cases. In particular, it is noticeable that the minimum in the post-deployment libration amplitude does not occur when the error on \(\theta _\mathrm{nadir,0}\) is null. This effect is due to the update of the “half-cosine” profile of the tether length rate at the end of the deployment to the profiles originated by the optimization process.

This section analyses show that, in all cases, the oscillation amplitude remains well below the required \(10^\circ\).

Fig. 18
figure 18

Time profiles of the out-of-plane libration angle \(\phi (t)\) (upper panel) and out-of-plane libration rate \({\dot{\phi }}(t)\) (lower panel) during the deployment and for an error at the out-of-plane release angle \(\epsilon _{\phi _0}\) in the range 1–5\(^\circ\). For negative values of \(\epsilon _{\phi _0}\), the profiles are symmetric with respect to the x-axis

Full size image
Fig. 19
figure 19

Post-deployment in-plane (top) and out-of-plane (bottom) libration amplitude for cases with different errors on release angles \(\epsilon _{\phi _0}\) and \(\epsilon _{\theta _\mathrm{nadir,0}}\)

Full size image

4.4 Future development

The research group in Padova is developing a prototype of the tip-mass using off-the-shelf components, with the final aim of validating and testing the DM during the initial phase of the tip-mass deployment maneuver, with a particular focus on the sensor system used to estimate the deployment velocity and the ability to follow the reference profile [53]. The SPARTANS facility of the University of Padova [54,55,56] will be used to host the prototype of the DM, emulating a microgravity environment to test the functionality and the performance of the DM during the beginning of the deployment maneuver when the thrusters on board the tip-mass operate.

5 Conclusions

This paper presents the E.T.PACK tether deployer basic architecture, requirements, and tether deployment strategy. The deployer consists of the tether reel, a motorized pulley system, a cold gas actuator to provide linear momentum at the beginning of the deployment, and the dedicated electronics and other ancillary subsystems. The Deorbit Kit requirements have been selected in collaboration with the European Space Agency; they focus on the impact on spacecraft resources, on the tether deployment strategy and stability, and on the survivability of the kit to launch loads. The tether deployment strategy aims at achieving tether libration stability as well as at the optimization of the ejection system. The deployment trajectory developed is able to limit the final libration amplitude of the tether system to less than 10\(^\circ\) and requires an ejection system providing a thrust of \(F_\mathrm{thr}=0.4\) N for the first 64 s of operations. This allows a complete and safe deployment of about a 3-km-long tether in 1 h time.

An in-plane, straight-tether-only dynamic model was adopted to optimize the deployment trajectory that aligns the tether system within about 1\(^\circ\) from the local vertical at the end of a 1-h-long deployment. Finally, the validity of the reference trajectory has been proven by adding the effects of the tether flexibility and those of the out-of-plane dynamics, with pointing errors at the start of deployment expected of the E.T.PACK system.

The extensive set of results leads to the conclusion that adopting the derived reference profile allows for the tether system to be aligned at the end of deployment to about 1\(^\circ\) from the local vertical in the presence of release errors within the pointing accuracy provided by the attitude control system. These results satisfy the deployment requirements with margins.