Abstract
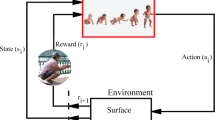
In this paper, a control algorithm based on Advantage Actor-Critic for the classical inverted pendulum system has been proposed. To enrich the observed states which are used to control, a CNN feature-based state is proposed. The direct control and the indirect control algorithms are introduced to address different control situations, such as the situation which only physical states like angle, velocity, etc. provided or the situation which only the indirect states provided like images, etc. A comparison experiment between the direct control and the indirect control algorithms based on the Advantage Actor-Critic has been evaluated. Besides, the comparison experiment with the Deep Q-Network algorithm has been performed. The experiment results show that the proposed method achieves comparable performance with the PID control algorithm and better than the Deep Q-Network based algorithm.
Similar content being viewed by others
References
Y. Y. Zhai, “A comparative study on the fuzzy control, LQR control and PID control of inverted pendulum,” Journal of Electronic Design Engineering, vol. 24, no. 7, pp. 116–119, April 2016.
H. C. Du, X. G. Hu, and C. Q. Ma, “Dominant pole placement with modified PID controllers,” International Journal of Control, Automation and Systems, vol. 17, no. 11, pp. 2833–2838, November 2019.
L. Zhou, J. H. She, and S. W. Zhou, “Robust H∞ control of an observer-based repetitive-control system,” Journal of the Franklin Institute, vol. 355, no. 12, pp. 4952–4969, August 2018.
L. Zhou, J. H. She, S. W. Zhou, and C. Y. Li, “Compensation for state-dependent nonlinearity in a modified repetitive control system,” International Journal of Robust and Nonlinear Control, vol. 28, no. 1, pp. 213–226, January 2018.
G. F. Jiang and C. P. Wu, “Inverted pendulum control based on Q-learning algorithm and BP neural network,” Journal of Acta Automatica Sinica, vol. 24, no. 5, pp. 662–666, May 1998.
C. J. C. H. Watkins and P. Dayan, “Q-learning,” Machine Learning, vol. 8, no. 3–4, pp. 279–292, May 1992.
V. Mnih, K. Kavukcuoglu, D. Silver, A. Graves, I. Antonoglou, D. Wierstra, and M. Riedmiller, “Playing atari with deep reinforcement learning,” arXiv preprint arXiv:1312.5602, December 2013.
H. van Hasselt, A. Guez, and D. Silver, “Deep reinforcement learning with double Q-learning,” Proc. of 30th AAAI Conference on Artificial Intelligence, 2016.
V. R. Konda and J. N. Tsitsiklis, “Actor-critic algorithms,” Advances in Neural Information Processing Systems, pp. 1008–1014, 2000.
V. Mnih, A. P. Badia, M. Mirza, A. Graves, T. Harley, T. P. Lillicrap, D. Silver, and K. Kavukcuoglu, “Asynchronous methods for deep reinforcement learning,” Proc. of International Conference on Machine Learning, pp. 1928–1937, 2016.
T. Schaul, J. Quan, I. Antonoglou, and D. Silver, “Prioritized experience replay,” CoRR abs/1511.05952, November 2015.
Z. Y. Wang, T. Schaul, M. Hessel, H. van Hasselt, M. Lanctot, and N. de Freitas, “Dueling network architectures for deep reinforcement learning,” Proc. of International Conference on Machine Learning, pp. 1995–2003, 2016.
T. P. Lillicrap, J. J. Hunt, A Pritzel, N. Heess, T. Erez, Y. Tassa, D. Silver, and D. Wierstra, “Continuous control with deep reinforcement learning,” Computer Science, vol. 8, no. 6, pp. A187, September 2015.
R. J. Williams, “Simple statistical gradient-following algorithms for connectionist reinforcement learning,” Machine Learning, vol. 8, no. 3, pp. 229–256, May 1992.
J. Kennedy and R. Eberhart, “Particle swarm optimization,” Proceedings of the IEEE International Conference on Neural Networks, vol. 4, pp. 1942–1948, December 1995.
G. Brockman, V. Cheung, L. Pettersson, J. Schneider, J. Schulman, J. Tang, and W. Zaremba, “OpenAI gym,” arXiv preprint arXiv:1606.01540, June 2016.
Author information
Authors and Affiliations
Corresponding author
Additional information
Recommended by Associate Editor David Banjerdpongchai under the direction of Editor Myo Taeg Lim.
Yan Zheng received her Ph.D., M.Eng. and B.Eng. degrees in control science and engineering from Northeastern University, China, in 2006, 1989, and 1984, respectively. She has been with the automation science in the school of information science and engineering at Northeastern University since 2000. Her research interests include variable structure control, intelligent control, fractional order system, machine learning and deep learning.
Xutong Li received her M.Eng. degree in control theory and control engineering from Northeastern University, China, in 2020. She received the B.Eng. degree in automation from Northeast Petroleum University, China, in 2017. Her research interests include computer vision, visual target tracking, machine learning and deep learning, reinforcement learning.
Long Xu received his M.Eng. degree in navigation guidance and control from Northeastern University, China, in 2019. He received his B.Eng. degree in automation from Inner Mongolia University, China, in 2016. His research interests include computer vision, visual target tracking, machine learning and deep learning, reinforcement learning.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Zheng, Y., Li, X. & Xu, L. Balance Control for the First-order Inverted Pendulum Based on the Advantage Actor-critic Algorithm. Int. J. Control Autom. Syst. 18, 3093–3100 (2020). https://doi.org/10.1007/s12555-019-0278-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12555-019-0278-z