Skip to main content
SpringerLink
Log in

A New Adaptive Neuro-sliding Mode Control for Gantry Crane

  • Regular Paper
  • Control Theory and Applications
  • Published:
International Journal of Control, Automation and Systems Aims and scope Submit manuscript

Abstract

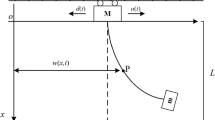
This paper presents a new adaptive neuro-sliding mode control for gantry crane as varying rope length. This control method derived from combining the sliding surfaces of three subsystem of the gantry crane (trolley position, rope length, anti-swing) to draw out two system sliding surfaces: the trolley position with the anti-swing and the rope length and the anti-swing. On the based of the sliding mode control principle, drawn out the equivalent controller and the switching controller for gantry crane. But due to the uncertain parameters-nonlinear model of gantry crane with the bound disturbances, combining the neural approximate method, defined the neural controller and the compensation controller for the difference between the equivalent controller and the neural controller for two system control inputs: trolley position and rope length. The adaptive control laws for these controllers were deduced from Lyapunov’s stable criteria to asymptotically stabilize the sliding surfaces. Simulation studies are performed to illustrate the effectiveness of the proposed control.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. P. Hahn, D. Chwa, and K. Hong, “A feedback linearization control of container cranes: varying rope length,” Interna tional Journal of Control, Automation and Systems, vol. 5, no. 4, pp. 379–387, 2007.

    Google Scholar 

  2. D. Liu and W. Guo, “Nonlinear controller design for the underactuated crane system,” International Journal of Control and Automation, vol. 6, no. 6, pp. 93–104, 2013.

    Article  Google Scholar 

  3. D. Qian and J. Yi, “Design of combining sliding mode controller for overhead crane systems,” International Journal of Control and Automation, vol. 6, no. 1, pp. 131–140, 2013.

    Google Scholar 

  4. A. Kaur, S. Kumari, and T. Singh, “Position control of overhead cranes using fuzzy controller,” International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering, vol. 3, no. 5, pp. 9341–9350, 2014.

    Google Scholar 

  5. A. Pal and R. K. Mudi, “An adaptive PD-type FLC and its real time implementation to overhead crane control,” International Association of Scientific Innovation and Research, vol. 13, 2013.

  6. M. Nazemizadeh, “A PID tuning method for tracking control of an underactuated gantry crane,” Universal Journal of Engineering Mechanics, vol. 1, no. 3, pp. 45–49, 2013.

    Google Scholar 

  7. J. Qiu, H. Gao, and S. X. Ding, “Recent advances on Fuzzy-Model based nonlinear networked control systems,” IEEE Transactions on Industrial Electronics, vol. 63, no. 2, pp. 1207–1217, 2016. [click]

    Article  Google Scholar 

  8. J. Qiu, S. X. Ding, H. Gao, and S. Yin, “Fuzzy model based reliable static output feedback H ∞ control of nonlinear hyperbolic PDE systems,” IEEE Transactions on Fuzzy Systems, vol. 24, no. 2, pp. 388–400, 2016. [click]

    Article  Google Scholar 

  9. A. Abe, “Anti-sway control for overhead cranes using neural networks,” International Journal of Innovative Computing Information and Control, vol. 7, no. 7, pp. 4251–4262, 2011.

    Google Scholar 

  10. J. Jafari, M. Ghazal, and M. Nazemizadeh, “A LQR optimal method to control the position of an overhead crane,” International Journal of Robotics and Automation, vol. 3, no. 4, pp. 252–258, 2014. [click]

    Google Scholar 

  11. H. Saeidi, M. Naraghi, and A. Asadollah, “A neural network self tuner based on input shapers behavior for anti sway system of gantry cranes,” Journal of Vibration and Control, vol. 19, no. 13, pp. 1936–1949, 2012.

    Article  Google Scholar 

  12. X. Shi and T. P. Zhang, “Sliding mode controls of doublependulum crane systems,” Journal of Mechanical Sciences and Technology, vol. 27, no. 6, pp. 1863–1873, 2013. [click]

    Article  Google Scholar 

  13. K. Huang and S. Zuo, “Neural network-based sliding mode control for permanent magnet synchronous motor,” The Open Electrical & Electronic Engineering Journal, vol. 5, no. 9, pp. 314–320, 2015. [click]

    Article  Google Scholar 

  14. D. Liu, J. Yi, D. Zhao, and W. Wang, “Swing-free transporting of two-dimensional overhead crane using sliding mode fuzzy control,” Proc. of American Control Conference, Boston, vol. 2, pp. 1764–1769, 2004.

    Google Scholar 

  15. S. Frikha, M. Djemel, and N. Derbel, “Observer based adaptive neuro-sliding mode control for MIMO nonlinear systems,” International Journal of Control, Automation and Systems, vol. 8, no. 2, pp. 250–256, 2010. [click]

    Article  MATH  Google Scholar 

  16. W. Chen, R. Li, and L. Jing, “Adaptive sliding mode control of container cranes,” IET Control Theory and Applications, vol. 6, no. 5, pp. 662–668, 2012. [click]

    Article  MathSciNet  Google Scholar 

  17. K. Choi and J. S. Lee, “Sliding mode control of overhead crane,” International Journal of Modeling and Simulation, vol. 31, pp. 203–209, 2011.

    Google Scholar 

  18. Y. Tao, J. Zheng, and Y. Lin, “A sliding mode control-based on a RBF neural network for deburring industry robotic systems,” International Journal of Advanced Robotic Systems, vol. 16, no. 8 pp. 1–10, 2016.

    Google Scholar 

  19. S. Sefriti, J. Boumhidi, R. Naoual, and I. Boumhidi, “Adaptive neural network sliding mode control for electricallydriven robot manipulators,” Journal of Control Engineering and Applied Informatics, vol. 14, no. 4, pp. 27–32, 2012.

    Google Scholar 

  20. L. Yugang and L. Yamgmin, “Dynamic modeling and adaptive neural-fuzzy control for nonholonomic mobile manipulators moving on a slope,” International Journal of Control, Automation, and Systems, vol. 4, no. 2, pp. 197–203, 2006.

    Google Scholar 

  21. W. He and S. Ge, “Cooperative control of a non uniform gantry crane with constrained tension,” Automatica, vol. 66, pp. 146–154, 2016. [click]

    Article  MathSciNet  MATH  Google Scholar 

  22. W. He, S. Zhang, Y. Ge, and Y. Li, “Adaptive control of a flexible crane system with the boundary output constraint,” IEEE Transactions on Industrial Electronics, vol. 61, no. 8, pp. 4126–4133, 2014. [click]

    Article  Google Scholar 

  23. J. Yu, Z. Peng, L. Cai, and B. Wu, “Adaptive control design for high-order MIMO nonlinear time-delay systems based on neural networks,” Scientific Journal of Control Engineering, vol. 4, no. 2, pp. 43–50, 2014.

    Google Scholar 

  24. D. Liu and L. Muguo, “Adaptive wavelet neural network backstepping sliding mode tracking control for PMSM drive system,” Automatica, vol. 55, no. 4, pp. 405–415, 2014.

    Google Scholar 

  25. S. Gao, J. Liu, Y. Li, K. Hong, and Y. Zhang, “Dual-layer fuzzy control architecture for the case rover arm,” International Journal of Control, Automation and Systems, vol. 13, no. 5, pp. 1262–1271, 2015. [click]

    Article  Google Scholar 

  26. H. Wong and A. Rad, “State observer based indirect adaptive fuzzy tracking control,” Simulation Modeling Practice and Theory, vol. 13, pp. 646–663, 2005. [click]

    Article  Google Scholar 

  27. Z. Du and T. Lin, “Adaptive fuzzy tracking control for MIMO uncertain nonlinear time-delay systems,” International Journal of Advancements in Computing Technology, vol. 3, no. 6, pp. 10–20, 2011.

    Article  Google Scholar 

  28. Y. Liu and Y. Li, “Sliding mode adaptive neural networks control for nonholonomic mobile modular manipulators,” Journal of Intelligent and Robotics Systems, vol. 44, no. 3, pp. 203–224, 2005. [click]

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Control and Energy Management Laboratory, Sfax University, Sfax, Tunisia

    Slim Frikha, Mohamed Djemel & Nabil Derbel

Authors
  1. Slim Frikha
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mohamed Djemel
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nabil Derbel
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Slim Frikha.

Additional information

Recommended by Associate Editor Huanqing Wang under the direction of Editor Hamid Reza Karimi.

Slim Frikha was born in Sfax (Tunisia) in 1970. He received his B.S. degree from the Ecole Supérieure des Sciences Techniques de Tunis (ESSTT) in 1996, and Doctorate degree in 2010 from the National School of Engineers of Sfax, Tunisia (ENIS). He is currently an assistant professor at the higher institute of industrial management of Sfax. His areas of interest include the stability, neural networks and adaptive control and observers.

Mohamed Djemel was born in Sfax (Tunisia), in 1963. He received his B.S. degree and the Diplôme d’Etudes Approfondies and Doctorat thesis in Electrical Engineering from the Ecole Supérieure des Sciences Techniques de Tunis (ESSTT), in 1987 and 1989, and 1996, respectively, and Habiltation Universitaire from the Ecole Nationale d’Ingénieurs de Sfax (ENIS) in 2006. He jointed the Tunisiaian University since 1990, where he held different positions involved in research and education. Currently, he is a Professor of Automatic Control at the Electrical Departement of the Ecole Nationale d’Inggénieurs de Sfax. His main research interests include the order reduction, the stability, the control and the advanced control of the complex systems.

Nabil Derbel was born in Sfax (Tunisia) in 1962.He received his engineering Diploma from the Ecole Nationale d’Ingénieurs de Sfax in 1986, the Diplôme d’Etudes Approfondies in Automatic control from the Institut National des Sciences Appliquées de Toulouse in 1986, the Doctorat d’Université degree from the Laboratoire d’Automatique et d’Analyse des Systèmes de Toulouse in 1989, and the Doctorat d’Etat degree from the Ecole Nationale d’Ingénieurs de Tunis. He joined the Tunisian University since 1989, where he held different position involved in research and education. Currently, he is a Full Professor of Automatic Control at the Ecole Nationale d’Ingénieurs de Sfax. His current interests include: optimal control, complex systems, fuzzy logic, neural networks, and genetic algorithms.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Frikha, S., Djemel, M. & Derbel, N. A New Adaptive Neuro-sliding Mode Control for Gantry Crane. Int. J. Control Autom. Syst. 16, 559–565 (2018). https://doi.org/10.1007/s12555-017-0070-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12555-017-0070-x

Keywords

Search

Navigation