Abstract
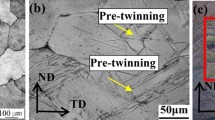
Effects of initial twins on dynamic torsional properties of extruded AZ31 alloy were investigated by introducing {10–12} twins into it through precompression to 3 and 6% strains along the extrusion direction and performing torsional testing at a strain rate of 1.4 × 103 s−1 using a torsional Kolsky bar system. The as-extruded sample without twins showed higher dynamic torsional properties than the precompressed samples with many initial twins; the maximum shear strength and fracture shear strain decreased with increasing amount of initial twins. In the as-extruded sample, twinning occurred vigorously throughout the gage section of the tubular specimen during high-strain-rate torsional tests, resulting in heavily deformed morphology, many macrocracks, and rough fractured surfaces. The increased amount of initial twins suppressed the twinning behavior and localized the applied torsional deformation; this resulted in an almost unchanged sample shape, no secondary cracks, and a flat fracture plane, thereby deteriorating the dynamic torsional properties of the extruded alloy.






Similar content being viewed by others
References
G.S. Rao, Y.V.R.K. Prasad, Mater. Sci. Eng. A 13, 2219 (1982)
S. Kleiner, P.J. Uggowitzer, Mater. Sci. Eng. A 379, 258 (2004)
L. Tang, C. Liu, Z. Chen, D. Ji, H. Xiao, Mater. Des. 50, 587 (2013)
J. Koike, T. Kobayashi, T. Mukai, H. Watanabe, M. Suzuki, K. Maruyama, K. Higashi, Acta Mater. 51, 2055 (2003)
S. Sandlöbes, S. Zaefferer, I. Schestakow, S. Yi, R.G. Martinez, Acta Mater. 59, 429 (2011)
A. Jain, S.R. Agnew, Mater. Sci. Eng. A 462, 29 (2007)
Y.N. Wang, J.C. Huang, Acta Mater. 55, 897 (2007)
M.R. Barnett, Mater. Sci. Eng. A 464, 1 (2007)
L. Wu, S.R. Agnew, Y. Ren, D.W. Brown, B. Clausen, G.M. Stoica, H.R. Wenk, P.K. Liaw, Mater. Sci. Eng. A 527, 7057 (2010)
X.Y. Lou, M. Li, R.K. Boger, S.R. Agnew, R.H. Wagoner, Int. J. Plast. 23, 44 (2007)
L. Wu, A. Jain, D.W. Brown, G.M. Stoica, S.R. Agnew, B. Clausen, D.E. Fielden, P.K. Liaw, Acta Mater. 56, 688 (2008)
G. Proust, C.N. Tomé, A. Jain, S.R. Agnew, Int. J. Plast. 25, 861 (2009)
R.E.R. Hill, R. Abbaschian, Physical Metallurgy Principles, 3rd edn. (PWS-Kent, Boston, 1994)
H.E. Kadiri, J. Kapil, A.L. Oppedal, L.G. Hector Jr., S.R. Agnew, M. Cherkaoui, S.C. Vogel, Acta Mater. 61, 3549 (2013)
L. Jiang, J.J. Jonas, A.A. Luo, A.K. Sachdev, S. Godet, Scr. Mater. 54, 771 (2006)
L. Jiang, J.J. Jonas, R.K. Mishra, A.A. Luo, A.K. Sachdev, S. Godet, Acta Mater. 55, 3899 (2007)
S.-G. Hong, S.H. Park, C.S. Lee, Acta Mater. 58, 5873 (2010)
M.R. Barnett, Z. Keshavarz, A.G. Beer, D. Atwell, Acta Mater. 52, 5093 (2004)
I. Karaman, H. Sehitoglu, A.J. Beaudoin, Y.I. Chumlyakov, H.J. Maier, C.N. Tome, Acta Mater. 48, 2031 (2000)
B. Song, R. Xin, G. Chen, X. Zhang, Q. Liu, Scr. Mater. 66, 1061 (2012)
Q. Dai, W. Lan, X. Chen, J. Eng. Mater. Technol. 136, 011005-1 (2013)
L. Jiang, J.J. Jonas, A.A. Luo, A.K. Sachdev, S. Godet, Mater. Sci. Eng. A 445–446, 302 (2007)
M. Knezevic, A. Levinson, R. Harris, R.K. Mishra, R.D. Doherty, S.R. Kalidindi, Acta Mater. 58, 6230 (2010)
S.H. Park, S.-G. Hong, C.S. Lee, Mater. Sci. Eng. A 578, 271 (2013)
S.-G. Hong, S.H. Park, C.S. Lee, J. Mater. Res. 25, 784 (2010)
S.H. Park, Mater. Sci. Eng. A 680, 214 (2017)
S.H. Park, S.-G. Hong, C.S. Lee, Mater. Sci. Eng. A 570, 149 (2013)
S.-H. Kim, S.-G. Hong, J.-H. Lee, C.S. Lee, J. Yoon, H. Yu, S.H. Park, Mater. Sci. Eng. A 700, 191 (2017)
S.H. Park, H.S. Kim, J.H. Bae, C.D. Yim, B.S. You, Scr. Mater. 69, 250 (2013)
C.H. Park, C.-S. Oh, S. Kim, Mater. Sci. Eng. A 542, 127 (2012)
G. Wan, B.L. Wu, Y.D. Zhang, G.Y. Sha, C. Esling, Mater. Sci. Eng. A 527, 2915 (2010)
F. Kabirian, A.S. Khan, T.G. Herlod, Int. J. Plast. 68, 1 (2015)
N. Guo, B. Song, C. Guo, R. Xin, Q. Liu, Mater. Des. 83, 270 (2015)
B. Song, C. Wang, N. Guo, H. Pan, R. Xin, Mater. 10, 280 (2017)
H. Chen, T. Liu, H. Yu, B. Song, D. Hou, N. Guo, J. He, Adv. Eng. Mater. 18, 1683 (2016)
B. Hwang, S. Lee, Y.C. Kim, N.J. Kim, D.H. Shin, Mater. Sci. Eng. A 441, 308 (2006)
H. Kolsky, Proc. Phys. Soc. 62B, 676 (1949)
A. Gilat, in ASM Handbook, vol. 8: Mechanical Testing and Evaluation, ed. by H. Kuhn, D. Medlin (ASM Int, Metals Park, 2000)
Y. Shiota, Y. Tomota, A. Moriai, T. Kamiyama, Met. Mater. Int. 11, 371 (2005)
H.S. Lee, B. Hwang, S. Lee, C.G. Lee, S.J. Kim, Metall. Mater. Trans. 35A, 2373 (2004)
D.G. Lee, S. Lee, C.S. Lee, Mater. Sci. Eng. A 366, 25 (2004)
C.S. Roberts, Magnesium and Its Alloys (Wiley, New York, 1960)
G.E. Dieter, Mechanical Metallurgy, SI Metric edn. (McGraw-Hill Book Co., Singapore, 1988)
P. Franciosi, Acta Metall. 33, 1601 (1985)
C.S. Pande, B.B. Rath, M.A. Imam, Mater. Sci. Eng. A 367, 171 (2004)
J. Zhang, Q. Yu, Y. Jiang, Q. Li, Int. J. Plast. 27, 768 (2011)
Y.-H. Zhao, J.F. Bingert, X.-Z. Liao, B.-Z. Cui, K. Han, A.V. Sergueeva, A.K. Mukherjee, R.Z. Valiev, T.G. Langdon, Y.T. Zhu, Adv. Mater. 18, 2949 (2006)
J. Marian, W. Cai, V.V. Bulatov, Nat. Mater. 3, 158 (2004)
M.A. Meyers, O. Vöhringer, V.A. Lubarda, Acta Mater. 49, 4025 (2001)
M.R. Barnett, Scr. Mater. 59, 696 (2008)
J.W. Christian, S. Mahajan, Prog. Mater Sci. 39, 1 (1995)
A. Ghaderi, M.R. Barnett, Acta Mater. 59, 7824 (2011)
N. Stanford, J. Geng, Y.B. Chun, C.H.J. Davies, J.F. Nie, M.R. Barnett, Acta Mater. 60, 218 (2012)
I. Ulacia, C.P. Salisbury, I. Hurtado, M.J. Worswick, J. Mater. Process. Technol. 211, 830 (2011)
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIP, South Korea) (No. 2016R1C1B2012140 and No. 2017R1A4A1015628).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Lee, J.U., Song, S.W., Kim, Y. et al. Effects of {10–12} Twins on Dynamic Torsional Properties of Extruded AZ31 Magnesium Alloy. Met. Mater. Int. 24, 283–289 (2018). https://doi.org/10.1007/s12540-018-0030-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12540-018-0030-x