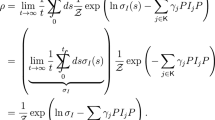Markovian statistics on evolving systems

Abstract

A novel framework for the analysis of observation statistics on time discrete linear evolutions in Banach space is presented. The model differs from traditional models for stochastic processes and, in particular, clearly distinguishes between the deterministic evolution of a system and the stochastic nature of observations on the evolving system. General Markov chains are defined in this context and it is shown how typical traditional models of classical or quantum random walks and Markov processes fit into the framework and how a theory of quantum statistics (sensu Barndorff-Nielsen, Gill and Jupp) may be developed from it. The framework permits a general theory of joint observability of two or more observation variables which may be viewed as an extension of the Heisenberg uncertainty principle and, in particular, offers a novel mathematical perspective on the violation of Bell’s inequalities in quantum models. Main results include a general sampling theorem relative to Riesz evolution operators in the spirit of von Neumann’s mean ergodic theorem for normal operators in Hilbert space.

Appendix: Proofs

For fundamental notions and facts on linear operators we refer to standard texts⁶ for fundamentals on linear operators.

1.1 Proof of Theorem 2

Recall the spectral representation for a continuous normal operator in its multiplication form:

Theorem 5

Let $\psi$ be a continuous operator on a complex Hilbert space ${{\mathcal {H}}}$ such that $\psi ^{*}\psi =\psi \psi ^{*}$. Then there exists a measure space $(\Omega ,\Sigma ,\mu )$, an essentially bounded measurable function $g:\Omega \rightarrow {{\mathbb {C}}}$ and a unitary operator $U:{{\mathcal {H}}}\rightarrow {{\mathcal {L}}}_{\mu } ^{2}(\Omega )$ such that

$$\begin{aligned} \psi =U^{*}M_{g}U, \end{aligned}$$

where M is the multiplication operator $M_{g}f=f\cdot g$. Moreover,

$$\begin{aligned} \Vert \psi \Vert =\Vert M_{g}\Vert =\Vert g\Vert _{\infty }. \end{aligned}$$

By Theorem 5, we can assume w.l.o.g.:

• ${{\mathcal {H}}}={{\mathcal {L}}}_{\mu }^{2}(\Omega )$ and $\psi$ is given as multiplication by a bounded measurable function g.

The stability of the evolution $\Psi =(\psi ,s)$ implies that there is a constant M so that $|g^n(\omega )f(\omega )| \le M$ holds almost everywhere for all positive integers n. It follows that a.e., $|g(\omega )| \le 1$ or $f(\omega ) = 0$. Hence there is a measurable function $g_1$ so that a.e., $|g_1(\omega )|\le 1$ and $g^n(\omega )f(\omega ) = g_1^n(\omega )f(\omega ).$ Setting

$$\begin{aligned} \overline{\psi }_{t}(f)=\left( \frac{1}{t}\sum _{m=1}^{t}g_1^{m}\right) f, \end{aligned}$$

we therefore conclude

$$\begin{aligned} |\overline{\psi }_{t}(f)(\omega )|^{2}\le \left( \frac{1}{t}\sum _{m=1} ^{t}|g_1(\omega )|^{m}\right) ^{2}|f(\omega )|^{2}\le |f(\omega )|^{2}. \end{aligned}$$

The sequence $(\overline{\psi }_{t}(f)(\omega ))_{t \ge 0}$ converges to

$$\begin{aligned} \pi (f)\left( \omega \right) =\left\{ \begin{array} [c]{cl} f(\omega ) &{} \text{ if } g_1(\omega )=1\\ 0 &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

If $g_1(\omega )=1$, then $\overline{\psi }_{t}(f)(\omega )=f(\omega )=\pi (f)\left( \omega \right)$, and so

$$\begin{aligned} \lim _{t\rightarrow \infty }\Vert \overline{\psi }_{t}(f)(\omega )\Vert _{2}= & {} \lim _{t\rightarrow \infty }\left( \int _{\Omega }|\overline{\psi }_{t} (f)-\pi (f)(\omega )|^{2}d\omega \right) ^{1/2}\\= & {} \lim _{t\rightarrow \infty }\left( \int _{g(\omega )\ne 1}|\overline{\psi } _{t}(f)\left( \omega \right) |^{2}d\omega \right) ^{1/2}. \end{aligned}$$

On the set $\{\omega \in \Omega \mid g(\omega )\ne 1\}$, the functions $|\overline{\psi }_{t}(f)(\omega )|^{2}$ converge pointwise to 0 and are bounded by the integrable function $|f(\omega )|^{2}$. The theorem of dominated convergence thus yields

$$\begin{aligned} \lim _{t\rightarrow \infty }\left( \int _{g(\omega )\ne 1}|\overline{\psi } _{t}(f)\left( \omega \right) |^{2}d\omega \right) ^{1/2}=\left( \int _{g(\omega )\ne 1}\lim _{t\rightarrow \infty }|\overline{\psi }_{t}(f)\left( \omega \right) |^{2}\right) ^{1/2}d\omega =0. \end{aligned}$$

Clearly, $\pi (f)$ is the orthogonal projection of f onto the eigenspace of $\lambda =1$. So stability is sufficient for mean ergodicity.

To see that stability is necessary for mean ergodicity, assume that

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{n}\sum _{k =0}^{n -1}T^{k}\left( f\right) \;\;\text{ exists } \text{ for } \text{ the } \text{ operator }\quad T\left( f\right) =\int gfd{\mu }. \end{aligned}$$

We would like to show that $\left| g\left( x\right) \right| \le 1$ holds a.e. on the set $\left\{ x :f\left( x\right) \ne 0\right\}$.

Assume that the set

$$\begin{aligned} M =\left\{ x :f\left( x\right) \ne 0\text {~}\ \text {and~}\ \text {}\text {}\left| g\left( x\right) \right|>1\right\} \end{aligned}$$

(14)

has positive measure. Then for some integer $r>1$ the set

$$\begin{aligned} M_{r} =\left\{ x :f\left( x\right) \ne 0\text {~}\ \text {and~}r>\ \text {}\text {}\left| g\left( x\right) \right|>1 +\frac{1}{r}\right\} \end{aligned}$$

(15)

has positive measure and for any $x \in M_{r}$, we have

$$\begin{aligned} \frac{1}{n}\sum _{k =0}^{n -1}T^{k}\left( f\right) =\frac{f\left( x\right) }{n}\sum _{k =0}^{n -1}g(x)^{k} =\frac{f\left( x\right) }{n}\frac{1 -g\left( x\right) ^{n}}{1 -g\left( x\right) }. \end{aligned}$$

(16)

Observing

$$\begin{aligned}&\left| 1 -g\left( x\right) ^{n}\right| \ge \left| g\left( x\right) \right| ^{n} -1>\left( 1 +\frac{1}{r}\right) ^{n}-1\\ \mathrm{and}\,&\left| 1 -g\left( x\right) \right| \le 1 +\left| g\left( x\right) \right| \le 1 +r, \end{aligned}$$

we thus conclude

$$\begin{aligned} \left| \frac{1}{n}\sum _{k =0}^{n -1}T^{k}\left( f\right) \left( x\right) \right| \ge \frac{\left| f\left( x\right) \right| }{n}\frac{\left( 1 +\frac{1}{r}\right) ^{n}-1}{1 +r} \end{aligned}$$

(17)

and hence

$$\begin{aligned}\left\| \frac{1}{n}\sum _{k =0}^{n -1}T^{k}\left( f\right) \right\| _{2}= & {} \frac{1}{n}\left( \int _{X}\left| \sum _{k =0}^{n -1}T^{k}\left( f\right) \left( x\right) \right| ^{2}\right) ^{1/2} \\\ge & {} \frac{1}{n}\left( \int _{M_{r}}\left| \sum _{k =0}^{n -1}T^{k}\left( f\right) \left( x\right) \right| ^{2}\right) ^{1/2} \\\ge & {} \frac{\left( 1 +\frac{1}{r}\right) ^{n}-1}{n\left( 1 +r\right) }\left( \int _{M_{r}}\left| f\left( x\right) \right| ^{2}d\mu \right) ^{1/2S}. \end{aligned}$$

Since $\int _{M_{r}}\left| f\left( x\right) \right| d\mu>0$ and $\lim _{n \rightarrow \infty }\frac{\left( 1 +\frac{1}{r}\right) ^{n}-1}{n\left( 1 +r\right) } =\infty ,$ it follows that $\left\| \frac{1}{n}\sum _{k =0}^{n -1}T^{k}\left( f\right) \right\| _{2}$ is unbounded. So the series $\left( \frac{1}{n}\sum _{k =0}^{n -1}T^{k}\left( f\right) \right) _{n>0}$ cannot converge. Consequently, $\left| g\left( x\right) ^{n}f\left( x\right) \right| \le \left| f\left( x\right) \right|$ and hence $\left\| T^{n}\left( f\right) \right\| _{2} \le \left\| f\right\| _{2}$ holds for all n. $\square$

1.2 Proof of Theorems 1 and 3

Throughout this section, let U be a fixed Banach space with a fixed element $s \in U$. We further fix an operator $T : U \rightarrow U$ that is bounded on $U_s = \text{ lin }\{T^n s : n\ge 0 \}$ and denote by $\hat{T}$ its (bounded) extension to $\hat{U}_s$. Without loss of generality, we can therefore assume $\hat{U}_s = U$ and $\hat{T} = T$. $\sigma (T)$ denotes the spectrum of T. The spectral radius of T is

$$\begin{aligned} r(T)=\max \{|\lambda |\mid \lambda \in \sigma (T)\} = \lim _{t\rightarrow \infty }\Vert T^{t}\Vert ^{1/t}\le \Vert T\Vert . \end{aligned}$$

Lemma 3

If T is Riesz, then $\sigma _1(T) =\{\lambda \in \sigma (T)\mid |\lambda | \ge 1\}$ is a finite set.

Proof

$\sigma _{\varepsilon ,\delta }(T) = \{\lambda \in \sigma (T) \mid \varepsilon \le |\lambda |\le \delta \}$ is a bounded subset of ${\mathbb C}$ for any $\varepsilon ,\delta \ge 0$. If T is Riesz, 0 is the only possible accumulation point of $\sigma (T)$. So $\sigma _{\varepsilon ,\delta }(T)$ must be finite for every $\varepsilon>0$. If T is bounded, $\sigma _1(T) = \sigma _{\varepsilon ,\delta }(T)$ holds for $\varepsilon = 1$ and $\delta = \Vert T\Vert$ and the claim of the Lemma follows. $\square$

For any eigenvalue $\lambda$ of T with finite algebraic multiplicity $n_\lambda$, the Riesz decomposition of T with respect to $\lambda$ guarantees⁷:

• (R) U admits the direct sum decomposition $U = N_\lambda \oplus R_\lambda$, where

  • 1. $N_{\lambda }=\{x\in U\mid (T-\lambda )^{n_{\lambda }}x=0\}$ is T-invariant with $\dim N_\lambda <\infty$;

  • 2. $R_{\lambda }=(T-\lambda )^{n_{\lambda }}U$ is T-invariant.

If $\sigma _1(T)$ is finite set of eigenvalues, repeated application of the Riesz decomposition (R) to some $\lambda \in \sigma _1(T)$ and then to $T:R_{\lambda }\rightarrow R_{\lambda }$ etc. and the other eigenvalues in $\sigma _{1}(T)$ yields

Lemma 4

(Riesz decomposition) If $\sigma _1(T)$ is a finite set of eigenvalues of T with finite algebraic multiplicities, then U admits a direct sum decomposition $U=N\oplus W$ into T-invariant subspaces N and W, where

$$\begin{aligned} N=\bigoplus _{\lambda \in \sigma _{1}(T)}N_{\lambda } \quad \text{ and }\quad \dim N <\infty . \end{aligned}$$

Moreover, $|\lambda | < 1$ holds for all eigenvalues $\lambda$ of the restriction of T to W. $\square$

The decomposition (R) implies that Riesz evolutions are finitary.

Proposition 2

Assume that T is a Riesz operator with decomposition $U = N\oplus W$ into T-invariant subspaces N and W such that $\dim N<\infty$ and the restriction of T to W has no eigenvalue in $\sigma _1(T)$. Then the Riesz evolution (T, s) is equivalent to the finite-dimensional evolution $(T, s_N$), where $s_N\in N$ is such that $s=s_N +s_W$ holds for some $s_W\in W$.

Proof

In view of $T^m s = T^m s_N + T^m s_W$ for all $m\ge 0$, it suffices to establish the claim

$$\begin{aligned} \lim _{n\rightarrow \infty } T^n s_W = 0. \end{aligned}$$

Since $\sigma _{\varepsilon , 1}(T)$ is a finite set for any $\varepsilon>0$, the spectral radius $r_W(T)$ of T on W must satisfy $r_W(T)< 1$. For clarity of notation, let $T_W$ be the restriction of T to W and choose $n_{0}$ so large that $\Vert T_W^{n}\Vert ^{1/n}\le r<1$ holds for all $n\ge n_{0}$. Then one has $\Vert T_W^{n}\Vert \le r^{n}$ and thus concludes

$$\begin{aligned} \lim _{n\rightarrow \infty }\left\| T_W^{n}s_W\right\| =0. \end{aligned}$$

$\square$

The proof of Theorem 1 is now immediate: The Riesz evolution $(\psi ,s)$ is equivalent to the finite-dimensional evolution $(\psi ,s_N)$. The ergodic properties stated in Theorem 1 are directly obtained by applying Proposition 1 to $(\psi ,s_N)$. $\square$

For the proof of the sampling theorem (Theorem 3), let (Q, x) be a finite-dimensional evolution that is equivalent to (T, s). So we have $\Vert T^ns-Q^nx\Vert \rightarrow 0$ and hence

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert f(T^ns) -f(Q^n x)\Vert = \lim _{n\rightarrow \infty } \Vert f(T^ns -Q^nx)\Vert = 0 \end{aligned}$$

since the sampling function f is continuous. This implies

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\sum _{m=1}^t \Vert f(T^ms) -f(Q^m x)\Vert =0, \end{aligned}$$

i.e., the f-sample averages converge on (T, s) exactly when they converge on (Q, x). It is furthermore clear that (T, s) is stable exactly when (Q, x) is stable. For the proof, we can therefore assume without loss of generality that already (T, s) is finite-dimensional and hence the sample space ${\mathcal F}= f(U_s)$ is finite-dimensional.

Passing to coordinates, we may thus assume: $U_s={\mathbb C}^n$ and ${\mathcal F}={\mathbb C}^k$. Since $f:{\mathbb C}^n\rightarrow {\mathbb C}^k$ is bounded on (T, s) if and only if each component functional $f_j$ of f is bounded on (T, s), it suffices to consider the 1-dimensional case $k=1$.

With respect to the chosen coordinatization, T is an $n\times n$ matrix, s a column vector and f a row vector of dimension n. Assume first that the sequence $(fT^ts)$ is bounded. Then

$$\begin{aligned} (fT^tu) \text {is bounded for every} u\in U_s = \text{ lin }\{T^ts\mid t=0,1,\ldots \} ={\mathbb C}^n. \end{aligned}$$

It follows that the sequence $(fT^t)$ of n-dimensional row vectors constitutes a bounded evolution. (The choice of u as the unit vector $e_i$ in ${\mathbb C}$ shows that the ith coordinate of the evolution is bounded.) In view of Proposition 1 (Section 2.1), this evolution is mean-ergodic. Consequently, the boundedness of $(fT^ts)$implies the existence of

$$\begin{aligned} \lim _{t\rightarrow \infty } \frac{1}{t}\sum _{m=1}^t fT^m \quad \text{ and } \text{ hence } \text{ of }\quad \overline{f}_\infty = \lim _{t\rightarrow \infty } \frac{1}{t}\sum _{m=1}^t fT^ms. \end{aligned}$$

To prove the converse implication, assume that $\overline{f}_\infty$ exists. Then

$$\begin{aligned} \displaystyle \frac{1}{t}\sum _{m=1}^t \lim _{t\rightarrow \infty } fT^mu \text {exists for every} u\in U_s = \text{ lin }\{T^ts\mid t=0,1,\ldots \} ={\mathbb C}^n. \end{aligned}$$

It follows that the evolution $(fT^t)$ of row vectors is mean ergodic and hence, again by Proposition 1, stable, i.e., there is some constant $c\in {\mathbb R}$ such that

$$\begin{aligned} |fT^ts| \le \Vert fT^t\Vert \cdot \Vert s\Vert \le c\Vert s\Vert < \infty \quad \text{ for } \text{ all } t\ge 0, \end{aligned}$$

which establishes the claim of the sampling theorem. $\square$