1 Introduction

Electronic performance and tracking systems (EPTS) [1] are emerging in many sports disciplines to support athletes and teams. EPTS measures players’ position velocity and acceleration. Performance indicators derived from those measurements are a widely used tool for practitioners to adapt athletes’ training or for sports media to enhance fan engagement by displaying players’ performance indicators. Specifically, EPTS are used to audit players’ physical load [2, 3] or computing advanced analytics from tracking data [4,5,6]. Generally, three technologies of EPTS systems have been established to capture players’ positioning and tracking data. Global Positioning Systems (GPS) are known for their high flexibility and portability for deployment in most outdoor settings. Local Positioning Systems (LPS) are used as they promise higher accuracy in position data. Semi-automatic video tracking systems (VID) are mainly used in high-level competitions not to impair the athletes during that time.

Typically, tracking is accomplished by different technologies in training and competition. Thereupon, tracking data from different EPTS must be interchangeable between systems, and uncertainties must be modelled to make training and competition comparable. In recent years, large-scale testing and validation studies of GPS [7,8,9], LPS [10,11,12,13,14] and VID [15,16,17] have been conducted and resulted in a deeper understanding of different error margins in different EPTS systems. Besides the accuracy of the EPTS system itself, sensor positioning and projection of the centre of mass have a substantial impact on the error dynamics of EPTS systems [18]. The different biomechanical limb behaviour while conducting specific exercises like sprinting, rapid changes in direction, decelerating, shuttle runs or even sport-specific exercises like lunges or tackles influence comparability.

For sprinting, Mero et al. [19] described, the continuous lifting of the upper body during the acceleration cycle, which has an impact on the velocity and acceleration profile of the athlete concerning the positioning of the EPTS sensor. Novacheck et al. [20] describe the forces and kinematics of running and outline the changes in kinematic parameters due to different athletic movement patterns, body types and stature of athletes. Recent work from Seidl et al. [21] extends biomechanical research by investigating the usage of LPS sensors in sprinting and the adoption of exercise analysis. Fitzpatrick et al. [22] showcased and visualized curved sprinting during football match-play and tried to quantify the sprint curve angle during football match-play. Nevertheless, they did not account for the positioning of the players’ inclination angle between feet and head. From the difference in exercise, the placement of the EPTS is crucial; therefore, Linke et al. [18] conducted a study to inspect the positioning of the reference position of the sensor to an infrared camera-based system by running a sport-specific course with multiple candidates. The study compared the measurements of the infrared camera-based system, taken at the centre between the shoulder (COS), the centre of pelvis (COP) and centre of mass (COM) and determined significant differences in velocity and acceleration according to the measurement point. A recent study by Blauberger et al. [11] solved the problem in the validation of different systems by attaching the reference system sensor close to the position of the sensor, which needs to be validated. However, this is just possible for GPS and LPS systems, where it is necessary to wear a sensor and does not make the system invariant to transformations, albeit it is well suited for the validation of systems. Additionally, practitioners use different systems, where the centre of mass, shoulder or pelvis are chosen locations to measure the performance indicators. Therefore, the question arises if it is possible to build a framework where different EPTS are comparable and errors based on biomechanical properties, and positioning can be minimized.

This study analyses the univariate and multivariate impact of kinematic parameters of athletes’ trajectories on the accuracy of different EPTS assessed by a gold standard ground truth. A gold standard, is a sensor measurement system validated and by magnitudes more accurate than the reference measurement. We suggest a multivariate division of accuracy with a clustering algorithm as current validation studies subdivide the error into specific univariate ranges [11, 12, 18]. Furthermore, with the practitioner in mind, this method allows to give semantic information to different tracklets. For instance, it is possible for the practitioner to identify critical movement patterns by analysing clustered trajectories that had similar kinematic properties. We interpret the placement of sensors and reformulate the systematic error when comparing different EPTS. Additionally, we suggest a mathematical model compensating the systematic error of EPTS to a gold standard and show the effects on performance indicators. Additionally, we introduce a method to transform speed and acceleration data recorded by a specific EPTS into the format of a different EPTS via the gold standard.

2 Methods

2.1 Data

The data used in this study was initially recorded in Augsburg, Germany, at the Rosenaustadion by the study of Linke et al. [12], where a more detailed description of the setup and used tracking methods can be found.

2.1.1 Participants

Fourteen male adolescent soccer players (age: 17.4 ± 0.4 years, height: 1.786 ± 0.042 m, weight: 70.2 ± 6.2 kg) playing for the FC Augsburg’s U17 in the German youth first league participated in the study. Prior to participation, all players received comprehensive explanations of the study. All players or their parents voluntarily signed informed consent to participate in the study. Institutional board approval for the study was obtained from the Ethics Commission of the Technical University of Munich. To ensure confidentiality, all performance data were anonymized. This study conformed to the recommendations of the Declaration of Helsinki. [12]

2.1.2 Testing systems

In this study, we included the video technology system of STATS: SportsVU, a high-definition, three-camera system working at 16 frames per second (Software: STATS SportVU version 2.12.0, build # 12351). The GPS is from GPSports (GPSports Sports Performance Indicator (SPI) Pro X, Canberra, Australia). The API provides raw position, instantaneous speed and distance data at 5 Hz and is upsampled to 15 Hz (Software: Team AMS firmware: R1 2015.10.). Inmotio (LPM system, 1 kHz, Inmotio Object Tracking BV, Amsterdam, Netherlands) is the compared LPS system Software: Inmotio Client, firmware: v3.7.1.153. The system is working with a sampling rate of 45.45 Hz.

2.1.3 Reference system

An infrared camera-based motion capture system VICON (VICON, Oxford, UK) captures reference positions for evaluating the testing systems. The setup contained 33 cameras, encompassing a field of 30 \(\times\) 30 m. Every player was equipped with five adhesive infrared markers on the right shoulder, left shoulder, right anterior superior iliac spine, left anterior superior iliac spine and sacrum. The spatial accuracy of the system is determined with a calibration rod that was tracked while being carried thoroughly through all sectors of the measurement area. The mean error of the calibrated VICON setup was 0.0 mm (SD = 1.0 mm 90 % CI [\(-\) 1.9 mm, +2.0 mm ]), resulting in a root mean square error (RMSE) of 1.0 mm at a frequency of 100 Hz.

2.1.4 Exercises

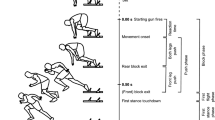
We focus on two kinds of exercises. Sport Specific Course (SSC) (Fig. 1) is a predefined circuit with different movement intervals, which are extremes of in-game movements and pose deliberately complex tracking tasks under controlled conditions. The course consists of different movement patterns: (1a) a 15 m sprint into (1b) a 5 m deceleration area, (2a) 20 m sprint into (2b) 10 m backwards running into (2c) 10 m forward running, (3) 505 agility test, (4) s-run, consisting of two rapid 90-degree turns (4a, b), (5) two curved runs in opposite directions that consist of alternating sprints and jogging back. This course can be observed in Fig. 1a. The beginning and end of each section are marked with pylons and VICON markers. This enables cross-validation of the start and end of each individual exercise based on players’ XY-position. For excellent comparability of EPTS, full-sized pitch games are best suited for testing under actual ecological conditions. As methods for full-pitch validation do not exist at the time of the study, we chose the best-suited alternative in a Small Sided Game (SSG) to compare the EPTS under natural conditions. The game consists of 5 vs 5 small-sided games without goals as a collective possession play on a 30 \(\times\) 30 m pitch. The games are split into repeated bouts of 2 min with 1 min of rest.

Fig. 1
figure 1

(a): SSC sample run on a 30 \(\times\) 30m pitch. The red dots describe the start and end of an exercise: (1a) 15 m sprint, (1b) 5 m deceleration, (2a) 20 m sprint, (2b) 10 m backwards running, (2c) 10 m forward running, (3) 505 agility test, (4a &b) s-run, (5) curved sprint, jogging back, sprint, jogging. (b): SSG sample run on a 30x30m pitch

Full size image

2.2 Data analysis

2.2.1 Preprocessing

To evenly sample the data prior to the error analysis, each system was sampled to 100 Hz. The timing offset between the trajectories is estimated by means of a cross-correlation procedure. Then the timing offset is aligned with the reference system. After temporal alignment, the reference system time code was set as a baseline for determining the beginning and end of sections in the sport-specific course. Data processing of raw VICON data consisted of filtering using a 4th order 10 Hz Butterworth low pass filter which is four times the Nyquist frequency of the GPS data. Hence, we are sure not to cut off signal. Gaps in the data of 1 to <10 ms were filled using spline interpolation. Gaps that were \(\le\)10 ms were excluded from the analysis. XY-positions for spatial accuracy analysis were derived from the 100 Hz VICON data. To account for the intra-cyclic kinematic parameter variations measured in the reference system due to its high resolution, the reference system was "gait neutralized" according to [12], as EPTS, in general, is meant to assess the gross movements of the players and not their biomechanics in detail. The gait-neutralized reference speed was calculated using a 4th-order 2 Hz Butterworth low pass filter on the raw reference system speed, according to the frequency-bandwidth that contains 99% of the FFT-transformed power in speed [12].

2.2.2 Kinematic parameters

To characterise the different kinds of errors, we hypothesise that the error corresponds to three different kinematic parameters of the running trajectory. As kinematic parameters of the trajectory, we define the player’s velocity, acceleration, and change of direction. Change of direction is a second instance kinematic parameter that must be computed from multiple velocity vectors around 3 points, in contrast to speed and acceleration provided by the systems. We need the velocity vector from the previous timestep and the following timestep around the current timestep.

$$\begin{aligned} \omega _1 = cos^{-1} \frac{\vec {v_0} \times \vec {v_1}}{|\vec {v_0}| |\vec {v_1}| } \end{aligned}$$
(1)

where \(\omega _1\) corresponds to the change of direction around point 1, and \(v_0\) and \(v_1\) correspond to the velocity vector from the previous point (p0) to the current point (p1) and from the current point to the following point (p2). While the reference-, video- and local positioning-system arrive at velocity by deriving the position of different players; the examined GPS derive the speed and acceleration data based on the Doppler shift effect. Hence, we recalculate the velocity vector from the position in GPS to recapture the direction but use the magnitude of the velocity directly from the GPS API. All data were extracted in the raw format of each tracking system for position, velocity and acceleration. For calculating the performance indicators, we neglected the indicators provided by the system and computed them on our own to verify consistency in the evaluation process.

2.3 Clustering of kinematic parameters

Extending the error analysis, we advocate a general way to classify univariate or multivariate error distributions. Previous studies tried to organize errors according to speed or acceleration intervals separately, more or less randomly chosen by the specific authors. In our research, we suggest doing this partitioning with a clustering algorithm. Additionally, this enables us to classify multiple kinematic parameters without, i.e. the exploding amount of classes due to the possible combinations of speed and acceleration that give semantic context (five speed classes and five acceleration classes as described in [11] would result in 25 combined classes to describe specific movements). Instead of defining the kinematic parameters in ranges, we use the mean and covariance of a Gaussian distribution to describe the different classes. The clustering is conducted with a Gaussian Mixture Model, optimized with the Expectation-Maximization algorithm. We subdivided our clustering approaches by minimizing the reconstruction with the Bayesian information criterion or semantic interpretation of the clusters by implying sport-specific priors on the kinematic parameters.

2.4 Regression analysis

Following our hypothesis that the error of different EPTS consists of three parts, namely the offset error by the placement of the reference point of the measurement or location of the sensor (1r), the resulting systematic error appears by the transformation of reference points due to the movement of the players (2r) and the non-systematic accuracy error of the EPTS resulting from variance in the technology behind the corresponding EPTS (3r).

1r and 2r are mostly viewed as single entities, as this fits the model of an almost rigid line between COM and COS. Otherwise, 1r can be incorporated in 2r as a combined systematic error 1r + 2r with \(f_{1r+2r}({\textbf{x}}) = f_{2r}(f_{1r}({\textbf{x}}))\) or any other function combination.

Example on error assumption As ground truth, we assume a simple sinusoidal movement (\(f_0(t) = sin(t)\)) in one direction around a specific point (i.e. in a human the COM, Fig. 2). If we measure this motion at a different point (i.e. the COS), we have a measurement error composed of the sensors’ offset and the motion coupling of the points, hence 1r and 2r. Further, we assume there is a zero mean Gaussian error \(\epsilon\) 3r, that is identical and independently distributed (i.i.d) and incorporated in the measurement device. Consequently, our new measurement function can be seen as \(f_\textrm{new} = f_1(f_0(t)) + c + \epsilon\).

Fig. 2
figure 2

a Example of a regression analysis: In blue, the ground truth sinusoidal movement (\(f(t) = \textrm{sin}(t)\), in orange, the nonlinear transformation (\(f_0(t) = b\cos (a f(t)) + c\) (1r, is the second term 8 c and 2r, is the first term of the right-hand side) of the ground truth and in green a noisy signal( \(f_n(t) = f_0(t) + \epsilon\) as provided by a sensor with sensor noise \(\epsilon\), 3r, that is sampled i.i.d. b Sensor placement model. Due to the different placement of sensors, i.e. VID vs. GPS, the sensor is recording different positions that can either be modelled with a biomechanical model or the model can be learned from recorded data. Between the sensors, we have different points of reference 1r and different movement characteristics 2r

Full size image

The notion of the split-up of errors results in the idea that different parts of the error are describable by polynomials concerning the kinematic parameters, size of the players and unknown physical properties of the closed tracking system. When describing the error from a probabilistic perspective, the error \(y \sim {\mathcal {N}}(\mu (x),\sigma ^2)\) is estimated with a Gaussian distribution, where the mean \(\mu (x)\) is dependent on different input parameters x and a not minimizable parameter \(\sigma\), which corresponds to the inexplicable, random error of the EPTS compared with a reference system. Furthermore, an optimal approximation of the problem maximises the likelihood of the function.

$$\begin{aligned} {\mathcal {L}}\left( \mu (x)|y\right) = \prod p\left( y_i|x_i\right) = \prod {\mathcal {N}}\left( y_i|\mu \left( x_i\right) , \sigma ^2\right) . \end{aligned}$$
(2)

This formulation is equivalent to a least square formulation of error estimation. It expresses the explainable part of the error to the mean and the noise resulting from measurement inefficiencies to the variance. When altering the descriptive function \(\mu (x)\), we can express a linear relation by \(\mu (x) = \beta _0 + \beta _1 x_1 + \beta _2 x_2 +...\) or model nonlinear relations with \(\mu (x) = f_n(x)\), where \(f_n(x)\) is a non-linear function, in our case a set of neural network architectures or in general any another non-linear polynomial. With this description, we want to estimate how much of the EPTS’s error consists of systematic errors like (1r) and (2r), which can be modelled with \(\mu (x)\) and (3r), which is included in \(\sigma ^2\).

2.5 Transformation of EPTS to a reference System

In Sect. 2.4, we argued that we could model the error of the EPTS. Consequently, the next step is to correct the error in the system. As a baseline for this error correction, we assume a linear regression model to convert specific kinematic parameters of one test system to the reference system. We compare this to nonlinear mapping and neural network approaches, which can incorporate temporal data. In [18], the movement of the body during the exercise of different tasks like sprinting and curve running have a different impact on the error associated with the given kinematic parameters. This transformation process increases the comparability of different EPTS, as the explainable error is reduced to a probabilistic minimum so that merely the random error occurs.

2.6 Transformation of EPTS via a reference system

Previously, we introduced the transformation of an EPTS to a reference system format via parametric models. It is difficult for clubs with multiple systems to receive consistent performance indicators over all the systems. A solution is always to transform all desired EPTS to a reference system and compute the performance indicators in that space. For two systems, the transformation computed by

$$\begin{aligned} {\textbf{x}}_{\text {tg1}}&= f_{t1}\left( {\textbf{x}}_{\text {EPTS1}}\right) \end{aligned}$$
(3)
$$\begin{aligned} {\textbf{x}}_{\text {tg2}}&= f_{t2}\left( {\textbf{x}}_{\text {EPTS2}}\right) , \end{aligned}$$
(4)

where the \({\textbf{x}}\) denotes the parameter vector, f the learned transformation function, the subscript tgi denotes the transformed gold standard/reference system for the system i and the subscript EPTSi denotes the correspondence of the parameter vector to the specific system. In this study, we compute how the error evolves when comparing two systems by comparing the error before and after transformation. A well-learned representation should fulfil Eq. 5 where \({\mathcal {L}}\) denotes the specific error corresponding to the parameter.

$$\begin{aligned} {\mathcal {L}}\left( {\textbf{x}}_{\text {tg1}}, {\textbf{x}}_{\text {tg2}}\right) < {\mathcal {L}}\left( {\textbf{x}}_{\text {EPTS1}}, {\textbf{x}}_{\text {EPTS2}}\right) . \end{aligned}$$
(5)

In Fig. 3, a visualization of this concept is displayed. It is possible to add any number of new EPTS in linear time.

Fig. 3
figure 3

Reference (Gold Standard) System transform scheme: by adding the transformation model to any EPTS, computed values are more comparable than directly comparing the values due to lower errors. The blue squares correspond to \({\textbf{x}}_\textrm{tgX}\) and the yellow and orange square to \({\textbf{x}}_\textrm{EPTSX}\)

Full size image

3 Results

The results are structured in six separate subsections. Statistical analysis of the different EPTS with respect to the reference system (1), the univariate analysis and dependencies of the error (2), the multivariate analysis of the corresponding error (3), the examination of the clustering algorithm by classification of the error (4), the transformation of any EPTS to the reference system (5) and the comparison of EPTS in the transformed reference system space (6).

3.1 Statistical analysis of data

We focus on the accuracy of the velocity and acceleration of the system compared to the processed reference system. Accuracy is computed by the root mean square error (RMSE) over the total dataset in SSC and SSG. Distinguishing between velocity root mean square error (vRMSE) and acceleration root mean square error (aRMSE) for the different systems leads to Table 1. To determine the significance of the measurement errors from zero, we conducted repeated measurements of ANOVA. For all systems, we computed a p-value < 0.001 and a large effect size \(\eta ^2\ge 0.26\) [12]. For speed, the GPS data is the most accurate (SSC-mean: 0.21 m/s, SSG-mean: 0.27 m/s), while the most precise is the LPM (SSC-std: 0.23 m/s. SSG-std: 0.24 m/s) [23]. For acceleration, the LPM data is the most accurate and precise (SSC: 0.45 ± 0.55 m/s\(^2\), SSG: 0.27 ± 0.49 m/s\(^2\)).

Table 1 Statistical error of systems with respect to the gold standard
Full size table

3.2 Univaritate regression of error

Here, we investigate the dependencies between different variables and the error measures. This experiment shows the relationship between

$$\begin{aligned} q&\sim x\textrm{RMSE}, \end{aligned}$$

where q corresponds to velocity, acceleration or COD and xRMSE corresponds to the respective error measure. In the case of univariate linear dependencies of error, a strong relationship between velocity and acceleration with respect to the vRMSE for all systems is arguable. The change of direction (COD) does not depend linearly on any error, nor in higher dimensions, equivalent to the low \(R^2\) score \(0.0 \le \rho \le 0.04\) with non-linear neural network architecture. Based on our findings, linear and non-linear models do not differ much in regression accuracy.

3.3 Multivariate regression of error

In multivariate regression of the error, we transform the input variables speed, acceleration and COD onto the different errors. Hence, we predict the error corresponding to the kinematic parameters in the form \(v/a\textrm{RMSE} = f(v, a, \omega )\). We can identify similar relations in the multivariate regression as in the univariate case. In Table 2, we can see that when the curve fitting is conducted with a neural network, the \(R^2\)-value more than doubles for almost every EPTS, resulting in a better approximation of the error with a non-linear model. The mean squared error (MSE) describes the error of the specific regression method and gives an intuition of how well the model fits. A large MSE corresponds to a bad fit, and a small MSE corresponds to a good fit. It is more sensitive to outliers than the RMSE and represents the variance plus bias of an estimator. We can describe the variance with the MSE [24] with an unbiased estimator. With the linear regression, we observe statistical significance for speed and acceleration (\(P(t)<0.0001\)), yet no significance in COD. While we can see in the VID system that the MSE for vRMSE is reasonably tiny at 0.147, it is relatively large for the aRMSE. This indicates that there are more significant differences in acceleration than in velocity. This can be seen in Fig. 5 due to the more considerable difference in box plot bars. The neural network structure (MLP) consists of one hidden layer with 50 neurons, Relu activation function, trained with stochastic gradient descent. Training and validation were done with a 10-fold cross-validation on the whole training data, while the split between training data and test data can be looked up in the online supplementary material for the respective experiments.

Table 2 Multivariate regression of error. Input variables are speed, acceleration and COD, and the regression target is *RMSE. Inspected models are a linear regression model and an MLP with one hidden layer and 50 neurons in that layer
Full size table

3.4 Clustering of kinematic parameters

Clustering was conducted with all SSC data. BIC scores between 3 and 4 clusters are identical for three variables, including all chosen kinematic parameters. Another way to select the number of clusters is to incorporate a priori information; by using experience and interpretability of the data as prior. We settled on 4 clusters, which is in line with the BIC criterion. In Fig. 4, the clusters are displayed with respect to the kinematic parameters for SSC and SSG. We can see the different tracklets moving through the clusters according to their kinematic parameters. The distribution of # points per cluster is 46 % for Cluster 0, 26% for Cluster 1, 23% for Cluster 2 and 6% for cluster 3 for the SSC. In SSG, we receive a different behaviour with 45% in Cluster 0, 20% in cluster 1, 16% in cluster 2 and 19 % in Cluster 3. The highest change of direction (COD) movements are conducted at a low speed and low acceleration, while at high velocities and accelerations, no fast changes in direction occur.

Fig. 4
figure 4

Cluster of error zones chosen by the components at the example of on sport specific course. For 4 clusters, the resulting association is: 0. low speed, acceleration and COD (salmon-red), 3. low speed and acceleration with large variance in COD (gold), 1. variance in speed and positive acceleration with low COD (green), 2. variance in speed and negative acceleration with low COD (azure). For 3 Cluster, the association is: 0. Low speed, acceleration and COD (salmon-red), 2. variance and speed, mainly positive acceleration, low COD (azure), 1. variance in speed and COD and negative acceleration (green)

Full size image

The mean error in the different clusters are depicted in Table 3. Clusters 1 and 2 have a more considerable error than clusters 3 and 0, while cluster 3 has a significantly larger error in acceleration than cluster 0; the velocity errors are closer. The velocity and acceleration errors larger in SSC than SSG for all systems in clusters 1 and 2, as there are large gradients in the respective kinematic parameter.

Table 3 Velocity and acceleration root mean square error of test systems according to the different clusters
Full size table

3.5 Transformation of EPTS trajectory to reference system trajectory

Transformation of velocity and acceleration trajectories is investigated with a linear regression model, a neural network with one hidden layer, 100 neurons, Relu activation function, a three-layer CNN with 32 channels and a kernel size of 5 in each layer and Relu activation and a three-layer LSTM with 32 neurons is used to investigate the transformation of measurements. The static models (linear, feed-forward neural network) can use single data points as training data; CNNs and LSTMs need sequential input. Therefore, the size of the training set for the sequential model reduces by sequence length (50). For every model and every kinematic parameter, we receive a best model. In Table 4, we display the best model for the respective ETPS and kinematic parameters.

Table 4 Mean error reduction on the courses for different EPTS with respect to the reference system
Full size table

3.6 Comparison of EPTS in reference system space

To compare the EPTS in reference system space, we applied the best transformation models for small-sided course to the respective EPTS. We chose the small-sided course, as it covers a greater spectrum of movement than the small-sided games. As the validation study did physically not allow to record of two back-sensor-based positioning systems at once, it is possible to compare VID with GPS and VID with LPS but not GPS with LPS. In Table 5, the error reduction in % is displayed. The base value is the RMSE between the systems before the transformation to the reference system, compared to the RMSE between both systems after the reference system transformation.

Table 5 Mean error reduction on the SSC course between LPS-VID and GPS-VID for kinematic parameters speed and acceleration as well as performance indicators distance covered, maximal velocity and acceleration
Full size table

4 Discussion

As previous studies have shown that the error differs in different exercises (i.e. sprinting, curved running, agility test), we investigated the error in continuous space. Univariate linear regression of kinematic parameters yielded a relatively low correlation between the regression model and observed data (0.001 \(\le\) \(R^2\) \(\le\) 0.278), denouncing a relatively high noise-to-signal ratio. When examining non-linear relations with NNs, we observe a more substantial relation between velocity, acceleration and the respective errors. At the same time, there is no strong correlation between change of direction and any error. Linke et al. [18] reported that velocity and acceleration deviation change with the change of direction, speed and acceleration between COS and COP. In our analysis, the change of direction has a negligible impact on the deviation of the error. A viable explanation for that is, that the change of direction is almost \(<5^{\circ }\) in 95% of the observations due to the high sampling rate of the EPTS compared to the movement of the participants. Hence, acceleration and velocity are the most impactful kinematic parameters in the regression task.

For the multivariate regression of kinematic parameters to error, the linear model performs almost equally between all the EPTS. In Table 2, we can see that the non-linear model for multiple parameters increases the \(R^2\) value and, therefore, the fit of the model while decreasing the MSE. The overall higher \(R^2\) yields the assumption that the EPTS error is describable with a non-linear function. Replacing the regression target of the error with the respective reference system value for speed or acceleration yields a model which transforms EPTS kinematic parameters to reference system parameters. Overall, the CNN and NN perform better than the linear model.

We re-calculate the covered distance, maximum velocity, and maximum acceleration with the best model and compare them to the reference system. In SportsVU we reduced the error in the covered distance by 39.1 % and the error in maximum speed and maximum acceleration 51.1% and 57.4%, respectively. In the Inmotio-system, we reduced the error in the covered distance by 30.5 % and the error in maximum speed and maximum acceleration 18.5% and 30.0%, respectively. For the GPS of GPSports, we reduced the error in the covered distance by 50.7 % and the error in maximum speed and maximum acceleration 66.9% and 47.9%, respectively.

In Fig. 5, bar plots over the different clusters for the respective best models for each EPTS are displayed. We can see that the most significant reduction in error occurs in the clusters with high acceleration, either positive or negative (1 & 2), and with a large change of direction (3), even when the speed and acceleration are low. When all kinematic parameters are low in magnitude, the models barely correct any velocity but decrease the variance in acceleration error for the video system. When clustering the kinematic parameters in 3 classes, we observe the same behaviour, as the cluster with negative acceleration absorbs the cluster with high variance in COD. We suggest using the cluster approach with 4 clusters for descriptive behaviour. It increases transparency and is explainable, as intuitively, the error increases for extensive movements and decreases when the players are almost static.

Fig. 5
figure 5

Semantic association of the error to the 4 cluster model, where cluster 0 accounts for medium to low speed, acceleration and COD, cluster 1 accounts for deceleration and low COD, cluster 2 accounts for acceleration and cluster 3 accounts for high COD at low speed and acceleration. A corresponding model is displayed in Fig. 4 for SSC and SSG

Full size image

In Table 5, the error reduction between systems compared via the reference system is a valuable insight for clubs, federations and coaches to synchronize the data recorded via multiple systems by a single system to compute different performance indicators. In theory, this is not solely possible via a reference system but any system that allows recording synchronized data to perform the training of those transformations.

5 Conclusion

In this study, we examined the acceleration and velocity errors of three different EPTS. We suggested that the error of the EPTS is described in a multivariate fashion to capture the semantics of sport-like behaviour in the evaluation of the system. Here, we apply a clustering approach to the kinematic parameters, which gives us semantics to describe the error and assign different error characteristics to different parts of the trajectories. We could show that the error of specific EPTS compared to the reference system can be reduced by up to 60%, depending on the chosen EPTS. By transforming the EPTS into a reference system and comparing video data with GPS and LPS data, a significant improvement in error reduction between the systems could be observed, allowing clubs and coaches to implement their synchronization algorithms. We introduce a general recipe to transform the data by recording at least two EPTS synchronously, where one is the desired reference system. In the second step, a transformation model can be learned with the data. Eventually, all performance indicators can be calculated and reported in the reference system space with a reduced variation in parameters for the different systems.