Skip to main content
SpringerLink
Log in

Enhanced second-order Stark effect in twisted bilayer graphene quantum dots

  • Research Article
  • Published:
Nano Research Aims and scope Submit manuscript

Abstract

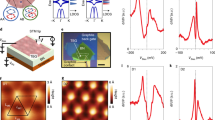
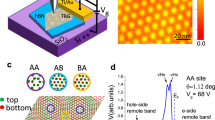
External electric field and interlayer twist introduce diverse changes in their confined electronic states of bilayer graphene quantum dots. Using a quantum-dot model, the band gaps of twisted bilayer graphene in finite sizes of about 1.4–2.4 nm with varying twist angles are studied in the presence of an electrostatic field perpendicular to the flakes by means of first-principles calculations. The size-dependent gaps are widened by the interlayer twist, but narrowed by the applied field. Their coupling, however, results in an enhanced Stark response in the twisted structures of which the field-induced band-gap variations are about 3–4 times as large as that of the corresponding untwisted structures under the same field strength. The exceptional Stark shifts come from the field-induced asynchronous shifts in their occupied and virtual energy levels, which are further enhanced by strong interlayer coupling at specific twist angles. Moreover, the shift of band gaps with the field strength follows the quadratic Stark response with large second-order shifting coefficients. The enhanced and tunable Stark shift suggests a gateway to the band engineering of bilayer graphene quantum dots by tuning their sizes, twist angles and their coupling with applied field.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bao, Q. L.; Loh, K. P. Graphene photonics, plasmonics, and broadband optoelectronic devices. ACS Nano 2012, 6, 3677–3694.

    Article  CAS  Google Scholar 

  2. Zhang, H.; Lv, X. J.; Li, Y. M.; Wang, Y.; Li, J. H. P25-graphene composite as a high performance photocatalyst. ACS Nano 2010, 4, 380–386.

    Article  CAS  Google Scholar 

  3. Sun, X. M.; Liu, Z.; Welsher, K.; Robinson, J. T.; Goodwin, A.; Zaric, S.; Dai, H. J. Nano-graphene oxide for cellular imaging and drug delivery. Nano Res. 2008, 1, 203–212.

    Article  CAS  Google Scholar 

  4. Ohta, T.; Bostwick, A.; Seyller, T.; Horn, K.; Rotenberg, E. Controlling the electronic structure of bilayer graphene. Science 2006, 313, 951–954.

    Article  CAS  Google Scholar 

  5. Latil, S.; Henrard, L. Charge carriers in few-layer graphene films. Phys. Rev. Lett. 2006, 97, 036803.

    Article  CAS  Google Scholar 

  6. Min, H.; MacDonald, A. H. Electronic structure of multilayer graphene. Prog. Theor. Phys. Supp. 2008, 176, 227–252.

    Article  CAS  Google Scholar 

  7. Zhou, S. Y.; Gweon, G. H.; Fedorov, A. V.; First, P. N.; De Heer, W. A.; Lee, D. H.; Guinea, F.; Neto, A. H. C.; Lanzara, A. Substrate-induced bandgap opening in epitaxial graphene. Nat. Mater. 2007, 6, 770–775.

    Article  CAS  Google Scholar 

  8. Kuzmenko, A. B.; Crassee, I.; van der Marel, D; Blake, P.; Novoselov, K. S. Determination of the gate-tunable band gap and tight-binding parameters in bilayer graphene using infrared spectroscopy. Phys. Rev. B 2009, 80, 165406.

    Article  CAS  Google Scholar 

  9. Ritter, K. A.; Lyding, J. W. The influence of edge structure on the electronic properties of graphene quantum dots and nanoribbons. Nat. Mater. 2009, 8, 235–242.

    Article  CAS  Google Scholar 

  10. Pan, D. Y.; Zhang, J. C.; Li, Z.; Wu, M. H. Hydrothermal route for cutting graphene sheets into blue-luminescent graphene quantum dots. Adv. Mater. 2010, 22, 734–738.

    Article  CAS  Google Scholar 

  11. Balog, R.; Jørgensen, B.; Nilsson, L.; Andersen, M.; Rienks, E.; Bianchi, M.; Fanetti, M.; Lægsgaard, E.; Baraldi, A.; Lizzit, S. et al. Bandgap opening in graphene induced by patterned hydrogen adsorption. Nat. Mater. 2010, 9, 315–319.

    Article  CAS  Google Scholar 

  12. Wu, H. C.; Chaika, A. N.; Huang, T. W.; Syrlybekov, A.; Abid, M.; Aristov, V. Y.; Molodtsova, O. V.; Babenkov, S. V.; Marchenko, D.; Sánchez-Barriga, J. et al. Transport gap opening and high on-off current ratio in trilayer graphene with self-aligned nanodomain boundaries. ACS Nano 2015, 9, 8967–8975.

    Article  CAS  Google Scholar 

  13. da Costa, D. R.; Zarenia, M.; Chaves, A.; Farias, G. A.; Peeters, F. M.; Analytical study of the energy levels in bilayer graphene quantum dots. Carbon 2014, 78, 392–400.

    Article  CAS  Google Scholar 

  14. da Costa, D. R.; Zarenia, M.; Chaves, A.; Farias, G. A.; Peeters, F. M. Magnetic field dependence of energy levels in biased bilayer graphene quantum dots. Phys. Rev. B 2016, 93, 085401.

    Article  CAS  Google Scholar 

  15. Giavaras, G.; Nori, F. Graphene quantum dots formed by a spatial modulation of the Dirac gap. Appl. Phys. Lett. 2010, 97, 243106.

    Article  CAS  Google Scholar 

  16. Trauzettel, B.; Bulaev, D. V.; Loss, D.; Burkard, G. Spin qubits in graphene quantum dots. Nat. Phys. 2007, 3, 192–196.

    Article  CAS  Google Scholar 

  17. Banszerus, L.; Frohn, B.; Epping, A.; Neumaier, D.; Watanabe, K.; Taniguchi, T.; Stampfer, C. Gate-defined electron-hole double dots in bilayer graphene. Nano Lett. 2018, 18, 4785–4790.

    Article  CAS  Google Scholar 

  18. Eich, M.; Pisoni, R.; Pally, A.; Overweg, H.; Kurzmann, A.; Lee, Y.; Rickhaus, P.; Watanabe, K.; Taniguchi, T.; Ensslin, K. et al. Coupled quantum dots in bilayer graphene. Nano Lett. 2018, 18, 5042–5048.

    Article  CAS  Google Scholar 

  19. Bockrath, M. Unprecedented charge state control in graphene quantum dots. Nano Lett. 2020, 5, 2937–2938.

    Article  CAS  Google Scholar 

  20. Miller, D. A. B.; Chemla, D. S.; Damen, T. C.; Gossard, A. C.; Wiegmann, W.; Wood, T. H.; Burrus, C. A. Band-edge electroabsorption in quantum well structures: The quantum-confined stark effect. Phys. Rev. Lett. 1984, 53, 2173–2176.

    Article  CAS  Google Scholar 

  21. Autler, S. H.; Townes, C. H. Stark effect in rapidly varying fields. Phys. Rev. 1955, 100, 703–722.

    Article  Google Scholar 

  22. Shafraniuk, S. E. Unconventional electromagnetic properties of the graphene quantum dot. Phys. Rev. B 2019, 100, 075404.

    Article  CAS  Google Scholar 

  23. Chattopadhyaya, M.; Alam, M. M.; Chakrabarti, S. On the microscopic origin of bending of grapheme nanoribbons in the presence of a perpendicular electric field. Phys. Chem. Chem. Phys. 2012, 14, 9439–9443.

    Article  CAS  Google Scholar 

  24. Guan, Z. Y.; Ni, S.; Hu, S. L. Tuning the electronic and magnetic properties of graphene flake embedded in boron nitride nanoribbons with transverse electric fields: First-principles calculations. ACS Omega 2019, 4, 10293–10301.

    Article  CAS  Google Scholar 

  25. Guo, Y. F.; Guo, W. L.; Chen, C. F. Tuning field-induced energy gap of bilayer graphene via interlayer spacing. Appl. Phys. Lett. 2008, 92, 243101.

    Article  CAS  Google Scholar 

  26. Zhang, Y. B.; Tang, T. T.; Girit, C.; Hao, Z.; Martin, M. C.; Zettl, A.; Crommie, M. F.; Shen, Y. R.; Wang, F. Direct observation of a widely tunable bandgap in bilayer graphene. Nature 2009, 459, 820–823.

    Article  CAS  Google Scholar 

  27. Xia, F. N.; Farmer, D. B.; Lin, Y. M.; Avouris, P. Graphene field-effect transistors with high on/off current ratio and large transport band gap at room temperature. Nano Lett. 2010, 10, 715–718.

    Article  CAS  Google Scholar 

  28. Lui, C. H.; Li, Z. Q.; Mak, K. F.; Cappelluti, E.; Heinz, T. F. Observation of an electrically tunable band gap in trilayer graphene. Nat. Phys. 2011, 7, 944–947.

    Article  CAS  Google Scholar 

  29. Ramasubramaniam, A.; Naveh, D.; Towe, E. Tunable band gaps in bilayer graphene-BN heterostructures. Nano Lett. 2011, 11, 1070–1075.

    Article  CAS  Google Scholar 

  30. Quhe, R.; Zheng, J. X.; Luo, G. F.; Liu, Q. H.; Qin, R.; Zhou, J.; Yu, D. P.; Nagase, S.; Mei, W. N.; Gao, Z. X. et al. Erratum: Tunable and sizable band gap of single-layer graphene sandwiched between hexagonal boron nitride. NPG Asia Mater. 2012, 4, e16.

    Article  CAS  Google Scholar 

  31. Castro, E. V.; Novoselov, K. S.; Morozov, S. V.; Peres, N. M. R.; dos Santos, J. M. B. L.; Nilsson, J.; Guinea, F.; Geim, A. K.; Neto, A. H. C. Biased bilayer graphene: Semiconductor with a gap tunable by the electric field effect. Phys. Rev. Lett. 2007, 99, 216802.

    Article  CAS  Google Scholar 

  32. Oostinga, J. B.; Heersche, H. B.; Liu, X. L.; Morpurgo, A. F.; Vandersypen, L. M. K. Gate-induced insulating state in bilayer graphene devices. Nat. Mater. 2008, 7, 151–157.

    Article  CAS  Google Scholar 

  33. Lee, K.; Fallahazad, B.; Xue, J. M.; Dillen, D. C.; Kim, K.; Taniguchi, T.; Watanabe, K. Tutuc, E. Chemical potential and quantum hall ferromagnetism in bilayer graphene. Science 2014, 345, 58–61.

    Article  CAS  Google Scholar 

  34. Woo, J.; Yun, K. H.; Chung, Y. C. Graphene monoxide bilayer as a high-performance on/off switching media for nanoelectronics. ACS Appl. Mater. Interfaces 2016, 8, 10477–10482.

    Article  CAS  Google Scholar 

  35. Velasco J. Jr; Lee, J.; Wong, D.; Kahn, S.; Tsai, H. Z.; Costello, J.; Umeda, T.; Taniguchi, T.; Watanabe, K.; Zettl, A. Visualization and control of single-electron charging in bilayer graphene quantum dots. Nano Lett. 2018, 18, 5104–5110.

    Article  CAS  Google Scholar 

  36. Cao, T. F.; Zheng, X. H.; Huang, L. F.; Gong, P. L.; Zeng, Z. Hydrogen-coverage-dependent stark effect in bilayer graphene and graphene/BN nanofilms. J. Phys. Chem. C 2014, 118, 10472–10480.

    Article  CAS  Google Scholar 

  37. Pedersen, T. G. Stark effect and polarizability of graphene quantum dots. Phys. Rev. B 2017, 96, 115432.

    Article  Google Scholar 

  38. Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magicangle graphene superlattices. Nature 2018, 556, 43–50.

    Article  CAS  Google Scholar 

  39. Cao, Y.; Fatemi, V.; Demir, A.; Fang, S.; Tomarken, S. L.; Luo, J. Y.; Sanchez-Yamagishi, J. D.; Watanabe, K.; Taniguchi, T.; Kaxiras, E. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 2018, 556, 80–84.

    Article  CAS  Google Scholar 

  40. Saito, Y.; Ge, J. Y.; Watanabe, K.; Taniguchi, T.; Young, A. F. Independent superconductors and correlated insulators in twisted bilayer graphene. Nat. Phys. 2020, 16, 926–930.

    Article  CAS  Google Scholar 

  41. Shi, H. H.; Zhan, Z.; Qi, Z. K.; Huang, K. X.; van Veen, E.; Silva-Guillén, J. Á.; Zhang, R. X.; Li, P. J.; Xie, K.; Ji, H. X. et al. Large-area, periodic, and tunable intrinsic pseudo-magnetic fields in low-angle twisted bilayer graphene. Nat. Commun. 2020, 11, 371.

    Article  CAS  Google Scholar 

  42. Kerelsky, A.; McGilly, L. J.; Kennes, D. M.; Xian, L.; Yankowitz, M.; Chen, S. W.; Watanabe, K.; Taniguchi, T.; Hone, J.; Dean, C. et al. Maximized electron interactions at the magic angle in twisted bilayer graphene. Nature 2019, 572, 95–100.

    Article  CAS  Google Scholar 

  43. Kim, K.; DaSilva, A.; Huang, S. Q.; Fallahazad, B.; Larentis, S.; Taniguchi, T.; Watanabe, K.; LeRoy, B. J.; MacDonald, A. H.; Tutuc, E. Tunable moiré bands and strong correlations in small-twist-angle bilayer graphene. Proc. Natl. Acad. Sci. USA 2017, 114, 3364–3369.

    Article  CAS  Google Scholar 

  44. Park, M. J.; Kim, Y.; Cho, G. Y.; Lee, S. Higher-order topological insulator in twisted bilayer graphene. Phys. Rev. Lett. 2019, 123, 216803.

    Article  CAS  Google Scholar 

  45. Uri, A.; Grover, S.; Cao, Y.; Crosse, J. A.; Bagani, K.; Rodan-Legrain, D.; Myasoedov, Y.; Watanabe, K.; Taniguchi, T.; Moon, P. et al. Mapping the twist-angle disorder and Landau levels in magic-angle graphene. Nature 2020, 581, 47–52.

    Article  CAS  Google Scholar 

  46. Rickhaus, P.; Wallbank, J.; Slizovskiy, S.; Pisoni, R.; Overweg, H.; Lee, Y.; Eich, M.; Liu, M. H.; Watanabe, K.; Taniguchi, T. et al. Transport through a network of topological channels in twisted bilayer graphene. Nano Lett. 2018, 18, 6725–6730.

    Article  CAS  Google Scholar 

  47. Deng, B. C.; Ma, C.; Wang, Q. Y.; Yuan, S. F.; Watanabe, K.; Taniguchi, T.; Zhang, F.; Xia, F. N. Strong mid-infrared photoresponse in small-twist-angle bilayer graphene. Nat. Photonics. 2020, 14, 549–553.

    Article  CAS  Google Scholar 

  48. Mirzakhani, M.; Peeters, F. M.; Zarenia, M. Circular quantum dots in twisted bilayer graphene. Phys. Rev. B 2020, 101, 075413.

    Article  CAS  Google Scholar 

  49. Tiutiunnyk, A.; Duque, C. A.; Caro-Lopera, F. J.; Mora-Ramos, M. E.; Correa, J. D. Opto-electronic properties of twisted bilayer graphene quantum dots. Phys. E: Low Dimens. Syst. Nanostruct. 2019, 112, 36–48.

    Article  CAS  Google Scholar 

  50. Tepliakov, N. V.; Orlov, A. V.; Kundelev, E. V.; Rukhlenko, I. D. Twisted bilayer graphene quantum dots for chiral nanophotonics. J. Phys. Chem. C 2020, 41, 22704–22710.

    Article  CAS  Google Scholar 

  51. Pan, D. Y.; Guo, L.; Zhang, J. C.; Xi, C.; Xue, Q.; Huang, H.; Li, J. H.; Zhang, Z. W.; Yu, W. J.; Chen, Z. W. et al. Cutting sp2 clusters in graphene sheets into colloidal graphene quantum dots with strong green fluorescence. J. Mater. Chem. 2012, 22, 3314–3318.

    Article  CAS  Google Scholar 

  52. Shen, J. H.; Zhu, Y. H.; Yang, X. L.; Zong, J.; Zhang J. M.; Li, C. Z. One-pot hydrothermal synthesis of graphene quantum dots surface-passivated by polyethylene glycol and their photoelectric conversion under near-infrared light. New J. Chem. 2012, 36, 97–101.

    Article  CAS  Google Scholar 

  53. Zhu, S. J.; Zhang, J. H.; Qiao, C. Y.; Tang, S. J.; Li, Y. F.; Yuan, W. J.; Li, B.; Tian, L.; Liu, F.; Hu, R. et al. Strongly green-photoluminescent graphene quantum dots for bioimaging applications. Chem. Commun. 2011, 47, 6858–6860.

    Article  CAS  Google Scholar 

  54. Forte, G.; Grassi, A.; Lombardo, G. M.; La Magna, A.; Angilella, G. G. N.; Pucci, R.; Vilardi, R. Modeling vacancies and hydrogen impurities in graphene: A molecular point of view. Phys. Lett. A 2008, 372, 6168–6174.

    Article  CAS  Google Scholar 

  55. Berashevich, J.; Chakraborty, T. Interlayer repulsion and decoupling effects in stacked turbostratic graphene flakes. Phys. Rev. B 2011, 84, 03340.

    Article  CAS  Google Scholar 

  56. Shen, J. H.; Zhu, Y. H.; Yang, X. L.; Li, C. Z. Graphene quantum dots: Emergent nanolights for bioimaging, sensors, catalysis and photovoltaic devices. Chem. Commun. 2012, 48, 3686–3699.

    Article  CAS  Google Scholar 

  57. Bistritzer, R.; Macdonald, A. H. Transport between twisted graphene layers. Phys. Rev. B 2010, 81, 245412.

    Article  CAS  Google Scholar 

  58. Jiang, Y. H.; Lai, X. Y.; Watanabe, K.; Taniguchi, T.; Haule, K.; Mao, J. H.; Andrei, E. Y. Charge order and broken rotational symmetry in magic-angle twisted bilayer graphene. Nature 2019, 573, 91–95.

    Article  CAS  Google Scholar 

  59. Sahu, B.; Min, H.; MacDonald, A. H.; Banerjee, S. K. Energy gaps, magnetism, and electric-field effects in bilayer graphene nanoribbons. Phys. Rev. B 2008, 78, 045404.

    Article  CAS  Google Scholar 

  60. Yanai, T.; Tew, D.; Handy, N. C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57.

    Article  CAS  Google Scholar 

  61. Chai, J. D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620.

    Article  CAS  Google Scholar 

  62. Frisch, M. J.; Pople, J. A.; Binkley, J. S. Self-consistent molecular orbital methods. 25. Supplementary functions for Gaussian basis sets. J. Chem. Phys. 1984, 80, 3265–3269.

    Article  CAS  Google Scholar 

  63. Ditchfield, R.; Hehre, W. J.; Pople, J. A. Self-consistent molecular orbital methods. 9. Extended Gaussian-type basis for molecular-orbital studies of organic molecules. J. Chem. Phys. 1971, 54, 724–728.

    Article  CAS  Google Scholar 

  64. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Petersson, G. A., Nakatsuji, H. et al. Gaussian 16, Revision C. 01; Gaussian, Inc.: Wallingford, CT, USA, 2016.

    Google Scholar 

  65. Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6169.

    Article  CAS  Google Scholar 

  66. Heyd, J.; Scuseria, G. E. Efficient hybrid density functional calculations in solids: Assessment of the Heyd-Scuseria-Ernzerhof screened Coulomb hybrid functional. J. Chem. Phys. 2004, 121, 1187–1192.

    Article  CAS  Google Scholar 

  67. Uchida, K.; Furuya, S.; Iwata, J. I; Oshiyama, A. Atomic corrugation and electron localization due to Moiré patterns in twisted bilayer graphenes. Phys. Rev. B 2014, 90, 155451.

    Article  CAS  Google Scholar 

  68. Egli, M.; Gessner, R. V. Stereoelectronic effects of deoxyribose O4′ on DNA conformation. Proc. Natl. Acad. Sci. USA 1995, 92, 180–184.

    Article  CAS  Google Scholar 

  69. Sarkhel, S.; Rich, A.; Egli, M. Water-nucleobase “stacking”: H-π and lone pair-π interactions in the atomic resolution crystal structure of an RNA pseudoknot. J. Am. Chem. Soc. 2003, 125, 8998–8999.

    Article  CAS  Google Scholar 

  70. Wang, J. J; Wang, Z. Y.; Zhang, R. J.; Zheng, Y. X.; Chen, L. Y.; Wang, S. Y.; Tsoo, C. C.; Huang, H. J.; Su, W. S. A first-principles study of the electrically tunable band gap in few-layer penta-graphene. Phys. Chem. Chem. Phys. 2018, 20, 18110–18116.

    Article  CAS  Google Scholar 

  71. Boyd, R. W. Nonlinear Optics, 3rd ed.; Academic Press: Waltham, 2008; p 25.

    Google Scholar 

Download references

Acknowledgements

The authors thank the financial support from the National Natural Science Foundation of China (Nos. 21773159 and 11904328).

Author information

Authors and Affiliations

  1. Institute of Atomic and Molecular Physics, Sichuan University, Chengdu, 610065, China

    Xian Wang, Li Zhang & Mingli Yang

  2. School of Physics and Electronic Engineering, Zhengzhou Normal University, Zhengzhou, 450044, China

    Yingqi Cui

Authors
  1. Xian Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yingqi Cui
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Li Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mingli Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mingli Yang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, X., Cui, Y., Zhang, L. et al. Enhanced second-order Stark effect in twisted bilayer graphene quantum dots. Nano Res. 14, 3935–3941 (2021). https://doi.org/10.1007/s12274-021-3318-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12274-021-3318-y

Keywords

Search

Navigation