Introduction

Estuaries are transitional zones located at the interface between the marine and terrestrial environment, and are characterized by complex hydrodynamics and sediment transport processes which result in a variety of geomorphological and ecological features (Feagin et al. 2009; Friedrichs 2011). Salt marshes are important coastal ecosystems frequently fringing the interior of estuaries, becoming established in low energy inter-tidal zones. Due to their location and vegetated surfaces, salt marshes offer several ecosystem services. For example, they can serve as sinks of sediments and pollutants and store large amount of carbon at a geological timescale; they can act as natural coastal defences and help mitigating coastal erosion by dissipating tidal currents and wind wave energy; they are the natural habitat of many plants and animal communities and also offer a place for recreational and tourist activities (Mudd et al. 2009, Temmerman et al. 2013, Leonardi et al. 2018).

The effectiveness of these vegetated surfaces for trapping fine particulates, together with biomass production, is the mechanism that allows salt marshes to keep pace with sea-level rise, and also influences the transport of pollutants within the estuary, with consequences for water quality, pollution of nearby areas and large-scale distribution of contaminants (Kirwan and Megonigal 2013). Flow deceleration (Ma et al. 2013), wave attenuation by friction on the salt marsh platform (Möller et al. 1999; Leonardi et al. 2016a) and turbulence dissipation (Neumeier and Ciavola 2004; Van Proosdij et al. 2006; Li and Yang 2009) within vegetation stems generally favour deposition and fine particle accumulation.

The potential of salt marshes to trap fine sediments, and consequently particle-bound pollutants, is especially relevant when dealing with highly contaminated waters coming from industrial and agricultural discharges (Ullrich et al. 2001; Soto-Jiménez and Páez-Osuna 2010; Wallschläger et al. 2000; Caborn et al. 2016; Fay and Knight 2016). Nutrient-rich waters also directly affect salt marsh ecosystems: on one hand, nutrients increase the above-ground biomass production, with consequent increase in energy dissipation by vegetation stems, and vertical accretion; on the other hand, they have been found to cause a decrease in below-ground production with consequent generation of weaker root-mats and increased salt marsh erosion rates and marsh block slumping (Deegan et al. 2012).

Salt marshes are also highly dynamic systems which are vulnerable to external agents, and there are uncertainties about their survival under current sea-level rise and possible increase in storm activities (Temmerman et al. 2004; Kirwan et al. 2010; Leonardi et al. 2016a). Existing studies demonstrate that salt marshes are generally able to maintain their vertical position; thanks to organic mass production and sediment trapping (Morris et al. 2002; Kirwan et al. 2010; D'alpaos et al. 2011; Fagherazzi et al. 2013); however, salt marshes are rarely stable in the horizontal direction, and sea-level rise poses a significant thread for their maintenance by increasing the accommodation space and the amount of sediment inputs required for marsh stability (Kirwan et al. 2010; Ganju et al. 2017). Salt marsh erosion has been commonly observed all around the world. For example, in the English coastal waters, the loss of salt marsh has been estimated around 83 ha/yr during the period of 1993–2013 (Phelan et al. 2011). For areas in the south west of the Netherlands and the Wadden Sea, cliff erosion up to 4 m/yr has been recorded (Bakker et al. 1993). In the USA, erosion rates around to 2 m/yr have been recorded for several locations along both the Atlantic and Pacific Coast (Schwimmer 2001; Marani et al. 2011; Fagherazzi 2013; Leonardi and Fagherazzi 2014; McLoughlin et al. 2015; Leonardi et al. 2016a, b). Apart from the loss of ecosystem services, the erosion of salt marshes is also associated with the risk of dispersal of contaminated sedimentary deposits, which can become a source of pollution for surrounding areas (Rahman et al. 2013). A significant erosion of salt marshes also modifies the hydrodynamics of the system, which might result in changes in sediment transport processes and variations in the net import or export of sediments.

The aim of this study is to evaluate sediment budget and sediment fluxes within tidal dominated estuaries, under different salt marsh erosion scenarios, based on numerical models. Here, sediment dynamics are used as a proxy for the movement of particle-bound contaminants. The Ribble Estuary, UK, is considered an important study site because of the risk associated with the redistribution of its highly radioactive salt marsh deposits. Special attention is given to the potential that salt marsh erosion has to modify the sediment transport in an estuarine system, by changing the net export of sediments, through the increase in tidal prism and bed shear stress across locations where the salt marsh has been eroded.

The manuscript is organized as follows: the “Study Area” section describes the study area, the “Methods” section focuses on the numerical model description and setup and the “Results” section presents results with regard to (i) changes in sediment fluxes under different salt marsh erosion scenarios, (ii) changes in the net sediment balance and (iii) changes in fluxes and sediment balance with different vegetation properties. A set of discussions and conclusions is finally presented.

Study Area

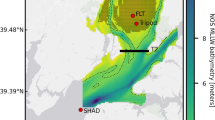
The Ribble Estuary (Fig. 1) is located in the north of Liverpool Bay, North-West of England, UK; the estuary is funnel-shaped, and tidally dominated with maximum diurnal tides up to 10 m (Wakefield et al. 2011). The ordinary tidal range in the estuary is 8.0 m at spring tide and 4.4 m at neap tide (UKHO 2001). As from the rest of Liverpool Bay, the Ribble Estuary is considered tidally dominated (Moore et al. 2009). The estuary experiences moderate wave energy, with waves generated in the relatively shallow Irish Sea; as the estuary is open to the west, the prevailing winds come from southerly and westerly winds (Pye and Neal 1994). The infilling of sediments from the bed of the Irish Sea, combined with the subsidiary contribution of silt and clay-size sediments coming from the River Ribble, resulted in the formation of extensive salt marshes on the South side of the estuary (Van der Wal et al. 2002; Lymbery et al. 2007).

Fig. 1
figure 1

a Computational mesh of the model. b Bathymetry of the Ribble Estuary. Model validation was carried out at the location depicted by the black dot, continuous black lines are where the net fluxes were calculated. c Contour lines indicate simulated salt marsh erosion scenarios (0% - current situation, 100% - salt marsh completely removed). Percentage reductions are based on LiDAR data. The two white dashed lines indicate two lateral boundaries where sediment fluxes are calculated. These two lines are also imposed on (a) and (b) as black solid lines. Distance from the Ocean boundary to the west open boundary of the model is 16.0 km, and it is 6.5 km from the Riverine boundary to the east open boundary

Full size image

Since 1952, Westinghouse Sellafield and Springfields Fuels Ltd. have been discharging radionuclides into the Irish Sea (Assinder et al. 1997; Tyler 1999). The radioactive pollutants have been dispersing away from the discharge points and depositing in the English, Scottish, Welsh and Irish coastal environments (Ryan et al. 1999; Charlesworth et al. 2006; Rahman et al. 2013). Among others, the Ribble Estuary has been reported to contain considerable inventories of radioactive contaminants in its sedimentary deposits (Mamas et al. 1995; Brown et al. 1999; Wakefield et al. 2011). For this reason, it is particularly important to understand whether possible salt marsh erosion scenarios originated as a consequence of sea-level rise, and changes in storm activities can lead to redistribution of sediments within the system and along the surrounding areas. Due to the large tidal range and its relatively regular and simple funnel-shaped geometry, the Ribble Estuary represents an exemplar macrotidal estuary with which to explore variations in sediment fluxes due to salt marsh erosion under the sole influence of tides.

Methods

The numerical model Delft3D which solves the unsteady shallow-water equations was used in 2DH mode to compute the depth-averaged flow and the transport of different sediment fractions. Delft3D uses a partially explicit-implicit finite difference method, and its numerical discretization follows orthogonal curvilinear grids. Sediment-transport and morphology modules account for the bed-load and suspended-load transport of multiple sediment fractions, either cohesive or non-cohesive, and for the exchange of sediments between the bed and the water column. The suspended load is evaluated through the advection–diffusion equation, and the bed-load transport is computed using empirical transport formulae. The bed-load transport formulation used in this work is the one proposed by (Van Rijn 1993). The model also takes into account the vertical diffusion of sediments due to turbulent mixing and sediment settling due to gravity. In case of non-cohesive sediments, the exchange of sediments between the bed and the flow is computed by evaluating sources and sinks of sediments near the bottom. Sediment sources are due to upward diffusion, whilst sediment sinks are caused by sediments dropping out from the flow due to their settling velocities (Van Rijn 1993). In case of cohesive sediments, the Partheniades–Krone formulations for erosion and deposition are used (Partheniades 1965).

The model Delft3D allows accounting for the effect of vegetation on the flow field by integrating the influence of vegetation stems into the momentum and turbulence equations. The effect of vegetation on the velocity field and on the vertical velocity structure is taken into account through an additional source term for friction, F(z), and additional terms for turbulent kinetic energy generation and dissipation. In this regard, plants are schematized as vertical cylinders whose most important characteristics include average stem diameters, stems density and height above the bottom (Rodi 1993; Baptist et al. 2007). A more detailed description about Delft3D and its implementation can be found in Deltares (Delft Hydraulics 2014).

The model domain, computational mesh and bathymetry of the study area are presented in Fig. 1a, b. The domain has a fan shape and the grid resolution is maximum within the river (cell size is ~ 20 m) and decreases seawards. The bathymetry of the model (Fig. 1b) is obtained from the combination of two datasets: bathymetric data for the open sea which have been downloaded from EDINA DIGIMAP and LiDAR data for the coastal regions which have been downloaded from the Environment Agency’s LiDAR data archive. The vertical reference levels of these two datasets are Low Astronomical Tide (LAT) and Above Ordnance Datum Newlyn (AODN), respectively. Therefore, before being combined together, the two sets have been adjusted and referred to MSL following spatially varying Vertical Offshore Reference Frame (VORF) corrections provided by the UK Hydrographic Office.

The input for the initial spatial distribution of sediments at the bottom was created from the British Geological Survey (BGS) GIS-maps for seabed sediments and parent material (near-surface geology) for the more landward side of the domain. Input sediment fractions include gravel, sand, very fine sand and mud (Table 1, Fig. 2). Offshore areas are sand-dominated with a large north-eastern portion characterized by high percentages of very fine sand. The interior of the estuary is mainly composed by very fine sand and mud sediment fractions. The model has two open boundaries: the west boundary is placed ~ 20 km offshore in the open sea to minimize possible open boundary effects whilst the east boundary crosses the River Ribble. Data for the west open boundary are provided by the Extended Area Continental Shelf Model fine grid (CS3X) which has 1/9° latitude by 1/6° longitude (approximately 12 km) resolution, and covers an area from 40° 07′ N to 62° 53′ N and from 19° 50′ W to 12° 50′ E. The CS3X model makes use of meteorological data from the UK Met Office Operational Storm Surge extended area surge model, and provides hourly water level and current simulation values. Input data at the east open boundary are provided as a time series of daily-averaged river discharge values, which were downloaded from the National River Flow Archive. The mean discharge for the simulated year is 44 m3/s. For simplicity, given that the main focus of the current research is to investigate tide-related mechanisms influencing the sediment transport within the estuary with an eroding salt marsh, the action of meteorological forcing and wind waves, are discussed in the final part of this manuscript. Similarly, density flow due to interaction between fresh water discharge and sea water has not been analysed. These topics might be the object of future studies.

Table 1 Parameters of the four sediment fractions
Full size table
Fig. 2
figure 2

Initial bed composition within the domain

Full size image

Model runs have been carried out by considering the present aerial extent of the salt marshes and five additional salt marsh erosion scenarios. The erosion scenarios consist in the removal of − 30%, − 50%, − 70%, − 90% and − 100% of the salt marsh vegetated surface. For cases accounting for salt marsh erosion, salt marsh removal is simulated by altering the bathymetry, i.e. replacing salt marsh bathymetry values with the ones of the surrounding tidal flats and by removing the vegetation. The initial bed composition of the aerial extent of the eroded salt marsh remains unchanged for different simulation scenarios.

Results

Model Validation

Since no tide gauge stations and data are available within the model domain, the performance of the model has been evaluated by comparing the model results with outputs from two other numerical models which have been previously and independently developed for areas including the Ribble Estuary by using the POLCOMS and the FVCOM modelling frameworks. The POLCOMS model includes the entire Liverpool Bay, and the FVCOM model includes Liverpool Bay as well as a part of the Irish Sea; therefore, both models include the study site. Both the POLCOMS and FVCOM models have been extensively validated against different tidal stations; among the others, the models have been calibrated using tide gauge measurements collected at the Liverpool Gladstone Dock station which is located at the mouth of the Mersey Estuary and is ~ 20 km south of the Ribble Estuary (further details of these two models see supplementary material).

A comparison between the water levels simulated using Delft3D, and the ones reproduced using the POLCOMS and FVCOM models is presented in Fig. 3 for one representative reference point (53.639 N, 3.133 W; black dot on Fig. 1b; ~ 8 km from the open boundary), and for the period from June 05, 2008; 00:00:00 a.m. to April 06, 2008; 00:00:00 a.m. The Delft3D model shows a good agreement with the other two models. The Brier Skill Scores (Murphy and Epstein 1989) with respect to the POLCOMS and FVCOM models are excellent, with 0.91 and 0.90 values, respectively. Harmonic analysis using Fast Fourier Transform has also been carried out to better quantify the model performance. In total, 29 tidal constituents were recognized by the analysis with the M2 and S2 harmonics being the dominant ones. For the reference point, Delft3D predicts tidal amplitudes which are slightly smaller than the ones obtained using the POLCOMS and FVCOM models (see Table 2). Slight changes in phase lag are also observed, especially for the M2 component, suggesting that the high tide in the Delft3D model is slightly delayed with respect to the results of the other two models. These discrepancies might be due to differences between the modelling framework, domain resolution and input bathymetry (see also supplementary material).

Fig. 3
figure 3

Comparison of POLCOMS, FVCOM and Delft3D modelled results. Location for this comparison is depicted as a black dot in Fig. 1b

Full size image
Table 2 Comparison between tidal amplitude and phase difference between the two major harmonics and for the three different modelling setups
Full size table

Suspended particulate matter in the Ribble Estuary was investigated by Wakefield et al. (2011). Specifically, field measurements of suspended sediment were collected at Warton Bank during the high water slack and the initial ebb period of a tidal cycle on the 17 July 2003 (spring tide without large fluvial flood). According to these measurements, the suspended sediment concentration within the estuary is vertically well mixed. Due to the lack of field measurements and data of suspended sediments for our study period, i.e. year 2008, data shown in Fig. 5 of Wakefield et al. (2011) are used as a reference to assess the model’s performance in regard to the magnitude of suspended sediments concentration. The mean concentration value over the data collecting period shown in Fig. 5 of Wakefield et al. (2011) is ~ 0.1 kg/m3. The time-averaged suspended sediment concentration estimated by the model at Warton Bank over the entire July of 2008 for periods ranging from slack water to part of the ebb tide, during which the river discharge is comparable, is 0.13 kg/m3. The model is thus able to reproduce suspended sediment concentration which are of the same order of magnitude as the ones measured by the field study, which is a satisfactory result in the absence of detailed measurements of suspended sediments.

Sediment Fluxes

As the salt marsh erodes, the tidal prism, i.e. the volume of water between mean high tide and mean low tide, gradually increases (Fig. 4a); the tidal prism increases by 1.4% once the salt marsh is completely removed; the bed shear stress in the estuary also increases, especially where the salt marsh is eroded and in the surrounding areas, whilst the rest of the domain experiences a negligible increase in bed shear stress (Fig. 4b). Figure 4c shows the distribution of changes in shear stress on the eroded salt marsh as well as over the entire model domain. It is observed that almost half of the eroded marsh area experiences an increase in bed shear stress higher than 0.5 N/m2, which is the critical shear stress for erosion for mud. On the other hand, Fig. 4d indicates that water levels within the estuary are only slightly influenced by salt marsh erosion. Hence, no strong changes are present in terms of tidal asymmetries, or tidal amplitudes, with the phase and the tidal range remaining almost the same.

Fig. 4
figure 4

a Tidal prism as a function of salt marsh erosion. b Changes in bottom shear stress during flood and spring tide with the passage from the 0% to the 100% erosion case; the small panel at the top represents a zoom-in view of the increased shear stress for the area where the salt marsh was eroded, i.e. white contour in the main panel. c Distribution of changes in shear stress on the eroded salt marsh (blue bars), and over the entire model domain (orange bars). d Water level near the Riverine boundary for the 0 and 100% erosion cases. The time series of data refers to the point indicated in b. Data in the figure refer to the flood period for a spring tidal cycle in March 10, 2008 (point indicated in b, white dot)

Full size image

To evaluate the sediment budget of the estuary under different salt marsh erosion scenarios, and to verify whether, for a fixed period, the system is characterized by a net export or import of sediments, we calculated sediment fluxes through two lateral boundaries (Fig. 1c, white dashed lines). The Riverine boundary is located at around 6 km from the open boundary of the domain, and its width is not influenced by salt marsh erosion. The calculation of the sediment fluxes was done by considering the average value of the fluxes through the boundary cells. For each cell, the fluxes were obtained by multiplying velocity, sediment concentration and water depth. The direction of the sediment fluxes was considered positive when sediments were entering the domain enclosing the salt marsh, and negative otherwise.

Figure 5 shows sediment fluxes at the Ocean and the Riverine boundaries for different salt marsh erosion scenarios (Fig. 1c). For visualization purposes, although the model was run for the entire year of 2008, and under the sole tidal influence, results presented in Fig. 5 refer to only one spring-neap tide cycle (10/03/2008 14:00:00 p.m. to 23/03/2008 02:00:00 a.m.); this period is more than 3 months after the initialization of the model which prevents the occurrence of spin-up effects (see also Fig. S2 in the supplementary material). As the model is tidally driven, sediment fluxes follow an oscillating behaviour, but the fluxes of sediments become almost negligible during neap tide. For the Ocean boundary, positive and negative fluxes are of the same order of magnitude and symmetrical, indicating that the resulting residual fluxes for this boundary are small. For the Riverine boundary, the sediment flux signal is asymmetrical, i.e. negative fluxes (exiting the domain) are much higher than the positive ones (entering the domain). This can be attributed to the funnelling shape of the estuary and its contraction effect on the flow field. During flood periods, the flow at the Riverine boundary is accelerated, and the sediment pick-up potential is strengthened, which results in stronger fluxes in comparison with the ones of the ebb period characterized by a jet-type dynamic with flow velocity rapidly decreasing seaward (Chen et al. 1990). It is also observed from Fig. 5 that sediment fluxes exiting the domain through the river boundary are always higher with respect to the fluxes exiting the Ocean boundary.

Fig. 5
figure 5

Sediment fluxes at the a Ocean and b Riverine boundaries. The location of the boundaries is indicated in Fig. 1c (white dashed lines). Positive values indicate an import of sediments (fluxes directed inside the domain); negative values indicate an export

Full size image

Changes in sediment fluxes under different salt marsh removal scenarios are also shown in Fig. 5. For the Ocean boundary, changes in salt marsh extent cause a significant enhancement of both positive and negative sediment fluxes. The level of enhancement is similar in both directions, and negative and positive fluxes at the Ocean boundary remain symmetrical. For the Riverine boundary, a reduction in the salt marsh area causes a large increase of the instantaneous sediment fluxes. However, differently from what was observed at the Ocean boundary, the increase in sediment fluxes exiting the domain through the Riverine boundary (negative values) is larger than those entering the domain through the same boundary. Therefore, the imbalance of import and export of sediments at the Riverine boundary is aggravated as a result of salt marsh retreat.

The impact of salt marsh retreat on the sediment fluxes is the most significant for a 30% removal of the marsh surface. Further reduction in the extent of the salt marsh (− 50 to − 100% removal) strengthens the changes in sediment fluxes but only negligibly in comparison with the − 30% case. This result suggests a non-linear relationship between sediment fluxes and salt marsh areal extent, i.e. the erosion of 30% of the salt marsh has effects comparable to its complete removal. Similar results in relation to net sediment fluxes can be found when considering a Riverine boundary located further away from the east open boundary (Fig. S4 in the supplementary material). Considering that salt marsh erosion does not significantly alter the tidal signal or create variations in tidal asymmetries, changes in sediment fluxes can be mostly attributed to the increase in bed shear stress for those areas where the salt marsh has been eroded.

The larger fluctuations in sediment fluxes associated with salt marsh erosion also suggest an increased potential of sediment exchange and movement within the estuary domain. Figure 6 shows the total mass of suspended sediment concentration within the domain enclosed by the two exterior boundaries for the same spring-neap tide cycle illustrated above. Results are presented for different percentage of salt marsh erosion. A large increase in the amplitude of suspended sediment fluctuation within the domain is observed as the salt marsh retreats, which suggests an increased likelihood of sediment movement, i.e. transport of sediment from one location to another. Again, in this case, the largest changes occur for a 30% reduction of the salt marsh surface. A further retreat of the salt marsh causes a negligible increase in fluctuations amplitude.

Fig. 6
figure 6

Total mass of suspended sediment in the domain enclosing the salt marsh. Results are presented for six salt marsh erosion scenarios: no marsh erosion, 30% marsh erosion, 50% marsh erosion, 70% marsh erosion, 90% marsh erosion and 100% marsh erosion

Full size image

Net Sediment Balance—Effect of Salt Marsh Erosion and Vegetation

To quantify the net import and export of sediments in the domain, the averaged fluxes through the Ocean and Riverine boundaries have been integrated over 120 representative tidal cycles (~ 2 months, from 23/02/2008 00:00:00 a.m. to 23/04/2008 00:00:00 a.m. This period is almost 3 months after the beginning of the numerical simulation; hence no spin-up influence on the results is expected. Figure 7 shows the net sediment import/export for three sediment fractions—sand, very fine sand and mud, as well as for their sum; positive values indicate a net import of sediments into the estuarine domain (boundaries in Fig. 1c), whilst negative values indicate an export of sediments. The net balance for the abovementioned 2 months is presented as a function of different salt marsh surface area reduction (0%—current situation, 100%—completely eroded salt marsh). Simulations have been run with (red lines) and without (black lines) vegetation. This allows separation of the influence of the salt marsh into two main mechanisms: the geometric effect connected to the sole change in estuarine geometry (increased estuary area) and the effects linked to vegetation. In fact, the presence of vegetation affects sediment transport patterns both directly and indirectly; vegetation stems can trap sediment and function as a sediment budget sink. Plants also affect the hydrodynamics by slowing down the flow field.

Fig. 7
figure 7

Net suspended sediment transport of a sand, b very fine sand, c mud and d total sediment at the two lateral boundaries (Ocean and Riverine boundaries indicated in Fig. 1) under the abovementioned six salt marsh erosion scenarios, from 0% (no salt marsh erosion) to 100% (salt marsh fully eroded)

Full size image

At the Ocean boundary, and for the present salt marsh configuration, a net import of 2.4 × 104 kg/m is estimated for the sand fraction (Fig. 7a). However, at the Riverine boundary, the net sand transport is negligible, meaning that there is almost no import/export of sand through this boundary. This is mainly due to the fact that sand is almost absent in the bed near the Riverine boundary. When the salt marsh is eroded, there is only a slight increase in the net sand import from the Ocean boundary, with the enhancement slightly more obvious at the beginning of salt marsh reduction. A 30 and 50% removal of the salt marsh causes a ~ 7 and ~ 13% increase in the net import of sand, but as the salt marsh continues to erode (70 to 100% marsh removal), there are no further changes in the import of sand. From Fig. 7a, it is also observed that changes in the sand import/export due the presence of vegetation are insignificant (red and black lines almost perfectly overlap).

For the very fine sand fraction (Fig. 7b), large exports of sediment through the Riverine boundary can be observed, whilst the net transport rates at the Ocean boundary are negligible. Independently from the presence of vegetation, as the surface area of the salt marsh reduces, the net export of sediments through the Riverine boundary increases (less sediments are retained inside the domain). The export of sediments changes non-linearly with the reduction in salt marsh surface area. The net export of very fine sand through the Riverine boundary is increased by ~ 15 and ~ 23%, respectively, for 30 and 50% of salt marsh erosion. However, after a 50% loss of the salt marsh, a further reduction of areal extent has very little effect. In regard to the impact of vegetation, the export of very fine sand in the presence of plants is more than four times smaller with respect to cases without vegetation (black lines). Again, for the vegetated cases, the relation between changes in export of very fine sand and reduction in salt marsh surface area is non-linear.

Similar to the behaviours of the very fine sand fraction, the mud sediment fraction (Fig. 7c) also demonstrates a large export of sediment through the Riverine boundary. However, the net transport rate of mud at this boundary is larger in comparison with the one of very fine sand. A net export of mud is also observed at the Ocean boundary. Both the Riverine and Ocean boundary are subjects to an increase in the export of the mud sediment fraction when the salt marsh is eroded. For muddy sediments, the presence of vegetation largely decreases the export of sediments, allowing more sediments to be retained within the domain (red lines are higher than the black ones). Results for the total sediment mass as the sum of the various sediment fractions is presented in Fig. 7d. It is observed that the net transport of total sediment is mostly driven by mud whose net transport rate is one order of magnitude higher with respect to the other sediment fractions.

To further investigate the impact of vegetation, we conducted a second set of numerical experiments with different plant densities and for the above-mentioned salt marsh erosion scenarios. For each salt marsh coverage scenario, five stem densities are applied: 0, 64, 128, 256 and 512 NP/m2 (number of plants/m2). Figure 8 shows net transport rates at the Ocean and Riverine boundaries as a function of different stem densities, and for different percentages of salt marsh erosion. The net sediment fluxes at the Ocean boundary show little dependence on vegetation density. In contrast, at the Riverine boundary, due to the narrow nature of the transect and its close proximity to the salt marsh, the net transport of very fine sand and mud, which are the sediment fractions with the highest transport rates, is sensitive to vegetation density. For very fine sand, the net transport rate at the Riverine boundary is reduced by more than a half when the salt marsh changes from bare land to vegetated surface with a stem density of 64 NP/m2. However, a further increase in vegetation density only slightly reduces the net export of sediments. The relation between net transport of cohesive mud and change in stem density of vegetation, on the other hand, is more linear. The net export of mud through the Riverine boundary reduces gradually as the number of plants distributed over the salt marsh surface increases. Going from a 0% vegetation coverage to a stem density of 512 NP/m2, the reduction in net mud transport is ~ 8%. However, the net export of mud at the Riverine boundary is one order of magnitude higher than the very fine sand one.

Fig. 8
figure 8

Net suspended sediment transport of a sand, b very fine sand, c mud and d total sediment at the two lateral boundaries (Ocean and Riverine boundaries indicated in Fig. 1) under five of the abovementioned salt marsh erosion scenarios, from 0% (no salt marsh erosion) to 90% (salt marsh erosion), with the salt marsh surface covered by vegetation of different stem densities

Full size image

Discussion

In some environments, salt marshes can subsist entirely on organic production, but for the majority of estuarine, and lagoon systems, the survival of salt marshes also requires input and storage of inorganic sediment in order to counteract erosive processes dictated by wave attack and tidal currents. Ultimately, the survival of salt marshes is a sediment budget problem, and the capability of the system to store sediments will govern whether the salt marsh complex tends toward expansion or contraction (e.g. Ganju et al. 2017). Increasing sea level further threatens salt marsh survival as it increases the amount of sediments required for stability (Crosby et al. 2016). Since salt marsh erosion is a common problem for many locations worldwide, it is reasonable to explore changes in the hydrodynamic and sediment transport patterns arising as a consequence of changes in salt marsh extent which might occur if external agents are unfavourable to salt marsh survival.

Results show that salt marsh erosion, i.e. reduction in areal extent, causes an increase in tidal prism and bed shear stress over the newly formed tidal flat areas replacing the former salt marsh. When the salt marsh is eroded, there are larger fluctuations in the fluxes of sediments in the estuary, which suggests an increased potential for sediment exchange and movement of particulate-bound pollutants within the estuarine basin. Furthermore, the net landward export of very fine sand and mud through the Riverine boundary is enhanced as a result of salt marsh retreat. The net export of sediments increases non-linearly with the percentage of salt marsh loss. A 30% erosion of the salt marsh surface has an impact on the sediment fluxes which is comparable to the one corresponding to a complete erosion of the salt marsh. Vegetation has been found to be an important element which promotes the trapping of sediments and reduces their landward export. Vegetation presence mainly influences the transport of the finest sediment fractions, and an increase in vegetation density (64 to 512 NP/m2) plays a secondary role with respect to the difference made by the sole presence of vegetation (0 to 64 NP/m2).

The underlying physical mechanisms responsible for changes in sediment patterns can be explained by considering that salt marsh erosion influences estuarine dynamics through changes estuarine geometry and removal of vegetated areas. Changes in estuarine geometry cause an increase in tidal prism, the generation of new tidal flats and changes in local flow patterns. Changes in tidal prism and local flow patterns can enhance the bed shear stress and suspended sediments across the extended estuarine area, outside from the eroded salt marsh footprint; the creation of new tidal flats on the footprint of the eroded salt marsh platforms leads to (i) continuous inundation and increase in bed shear stress of an area which was previously only inundated during high tide and previously characterized by relatively low shear stress values and (ii) creation of a new localized source of sediments.

For this study site, for the 100% erosion case, the area within the eroded salt marsh footprint undergoes an increase in bottom shear stress as large as 3.5 N/m2. The frequency distribution of shear stress increases is presented in Fig. 4c, and it shows that ~ 50% of the eroded area experiences an increase in bottom shear stress larger than 0.5 N/m2 which is the critical shear stress for the erosion of mud. The tidal prism also increases as the salt marsh erode (Fig. 4a), and this together with local changes in flow patterns explains the increase bottom shear stress across areas surrounding the newly formed tidal flats. For this test case, the increase in bed shear stress for areas distant from the footprint of the eroded salt marsh area appears negligible.

Tides in the upper part of the estuary are asymmetrical, featuring faster/stronger flooding phases and slower/weaker ebbing phases. Tidal asymmetry, in particular tidal phasing, has been identified as the major factor influencing sediment transport dynamics in estuaries (Dronkers 1986; Prandle 2009). For our study site, changes in tidal dynamics, e.g. tidal asymmetry enhancement, associated with the removal of the salt marsh are very small, even for areas very close to the eroded salt marsh and near the Riverine boundary (Fig. 4d). We suggest that these minimal changes in the tidal regime are unlikely to cause a substantial impact on the transport patterns in the estuary. Alternations in sediment transport are therefore mostly dictated by changes in bed shear stress across and nearby the footprint of the eroded salt marsh, which then acts as a localized sediment source.

Wind waves can be important for the transport of sediments in estuaries; for instance, wind waves can remobilize sediments from the seabed (Fernández-Mora et al. 2015; Brooks et al. 2017), and once in suspension sediments can be transported by tidal currents. Detailed analysis of wave processes is beyond the scope of this work which is focused on tide-driven sediment transport. However, given the possible relevance of wave action, a set of preliminary analysis has been conducted in this regard (Fig. S5 in the supplementary material). According to a series of additional numerical simulations including waves, which were conducted with the 90th percentile of the 2008 hourly wind record for eight different wind directions (0–360°), the Ocean boundary can experience a large increase in sediment export (up to 80%) when wind blows from the south-west, suggesting that waves enhance the resuspension of sediments and the magnitude of net sediment fluxes, whilst the direction of these net fluxes remains invariant. Differently, the Riverine boundary experiences negligible changes in net export/import (1%) of sediments with respect to the ‘no-wave’ scenario (Fig. S5). Density-driven currents are another factor possibly influencing sediment transport. The interaction between freshwater and seawater can generate density flows associated with salinity and temperature gradients. The importance of density flows in relation to sediment transport patterns includes seaward transport of fine sediment during seasons when water is highly stratified and dispersion of fine sediment due to density gradients in inlets (Castaing and Allen 1981). Density-driven currents, however, are also neglected in this study, and the absence of these currents could cause the seaward transport of fine sediments to be underestimated.

Results presented in this manuscript are important in consideration of numerous ecosystem service provided by salt marshes. The increased export of sediments as a result of salt marsh erosion might further enhance salt marsh erosion, creating a positive feedback which is detrimental for salt marsh survival. Results are also relevant within the context of sediments being a potential source of pollution. Indeed, estuaries around the world have been heavily exploited. Frequently, industrial developments have left behind accumulation of contaminants which have deposited in the form of particulate-bound pollutants through adhering to fine sediment of both salt marsh platforms as well as tidal flats; some of these, such as heavy metals and radioactive contaminants are less visible but extremely hazardous. Many existing studies have highlighted the high radionuclide absorptive capabilities of fine sediments (Stanners and Aston 1981; Livens and Baxter 1988; MacKenzie et al. 1999), and sediments within the Ribble Estuary specifically have been reported to contain a large accumulation of radioactive contaminants (Wakefield et al. 2011). From a coastal management perspective, one of the consequences connected to the changes in sediment transport dynamics due to salt marsh erosion is, therefore, an increased exposure of landward areas to the radioactive contaminants trapped within the estuary. Coastal management options should thus aim to maintain the existing salt marshes in order to reduce the risk of pollution for upstream areas.

Conclusions

Sediment budget and sediment transport dynamics in a tide-dominated estuary have been investigated using a process-based numerical model. The net balance of fine sediments within the Ribble Estuary, UK has been studied within the context of the high radioactive content, as well as particulate-bound contaminants present in the estuary. A special focus has been given to the influence salt marsh erosion exerts on sediment dynamics.

Salt marsh erosion and loss of areal extent has been found to intensify tidally induced fluctuations in suspended sediment, which suggests an increase in the potential movement of sediments within the estuary. It also intensified the landward export of fine sediment, with a possible increase in the upstream transport of contaminants.

The main underlying reason for this is the creation of tidal flats which, differently to salt marsh platforms, are continuously inundated and subject to higher shear stress values. Impact of salt marsh loss on tide regime, in particular tidal asymmetry, in the estuary is small, especially as no phase delay was observed. This leads to the conclusion that the enhanced net landward export of very fine sand and mud through the Riverine boundary can be attributed to the increase in sediment in suspension, i.e. more fine sediment originated from the eroded salt marsh will be transported to the upstream areas.

The impact of salt marsh erosion on the net export of sediments was found to be non-linear, i.e. the erosion of 30% of the salt marsh area had effects comparable to its complete removal. The influence of vegetation has also been explored; the presence of a vegetated surface increased the trapping of sediments within the estuary. For example, for very fine sand, the transition from a bare surface to a vegetated surface with 64 NP/m2 decreased the net landward export of sediments of around 50%. However, further increases in stems density (from 64 to 512 NP/m2) had a relatively small effect.