Influence of an External Perpendicular Oscillation on Stability of a Vertical Falling Liquid Film

Abstract

A vertical falling Newtonian liquid film flow is inherently unstable to surficial long-wave disturbances. Imposing external oscillation can stabilize the long-wave instability, but also triggers additional parametric instabilities. The effect of oscillation frequency on the stability is subtle. By using the “viscosity-gravity” scaling, the effect of oscillation frequency on the stability can be investigated exhaustively by separating it from other control parameters. In this paper, the effects of external perpendicular oscillation on the stability of a vertical falling liquid film are then investigated by a combination of linear stability analyses based on Floquet theory and numerical simulations with an unsteady weighted residual model (WRM). The linear analyses show that, increasing oscillation amplitude always has a stabilizing effect on the long-wave instability. On the other hand, increasing or decreasing oscillation frequency can suppress the long-wave instability, depending on whether the oscillation amplitude or the acceleration is fixed. The effect of varying oscillation frequency on the long-wave instability is opposite to that on the parametric instabilities. The long-wave and parametric instabilities compete with each other as the oscillation amplitude and frequency are varied with the Reynolds number fixed. A weakness of the long-wave instability always accompanies enhancements of the parametric instabilities, and vice versa. As a contrast, an increase of Reynolds number always results in more unstable long-wave and parametric instabilities. The numerical simulations with the WRM show that the wave amplitudes and the minimal local thickness of film are proportional to the unstable wavenumbers range rather than the growth rate of the instability. For a given oscillation frequency and Reynolds number, there exist a critical oscillation amplitude above which externally imposed oscillations perpendicular to the transversal direction of the film can also trigger a chaotic behavior in the film, just like what happens in the case where the oscillation is parallel to the stream-wise direction of the film.

Introduction

Thin liquid flow has a wide variety of applications in industry, such as heat exchangers, evaporative cooling, condensers, coating (Colinet et al. 2001). When a Newtonian viscous liquid thin film falls down freely along a vertical plane, it is inherently unstable to surficial long-wave disturbances (Yih 1963; Benjamin 1957; Kapitza and Kapitza 1949). The instability is welcome or undesirable, depending on the applications of the film flows. Controlling the long-wave instability is theoretically and practically important, and has received a lot of attentions since the pioneering work of Kapitzas (Kapitza and Kapitza 1949) in 1949.

Applying external oscillation has been used to control flow stabilities (Hall 1978; Kerczek 1982; Singer et al. 1989; Woods and Lin 1995). Hall (1978), Kerczek (1982), and Singer et al. (1989) have investigated separately the stability of the classical Poiseuille flow by applying a temporally oscillating stream-wise pressure gradient to the steady Poiseuille flow. Their studies showed that the stream-wise temporally periodic modulation can make the steady flow more stable, depending on the frequency of the oscillation. The theoretical analyses of Hall (1978) and Kercszek (1982) showed that modulation may play a destabilized effects if the frequency is very high. On the other hand, the simulations carried out by Singer et al. (1989) showed that harmonic pulse has a destabilizing effect on the steady flow if the frequency is very low. It can be seen that the effect of oscillation frequency on the stability of flow is subtle.

Woods and Lin (Woods and Lin 1995) investigated the effect of oscillations perpendicular to the plane on the stability of a vertical falling thin film and showed that the imposition of oscillations can suppress, but can’t completely eliminate the long-wave instability. Meanwhile, oscillation can introduce a new instability: parametric instability, which is also known as parametric resonance. The essential mechanism of parametric resonance is the resonance between the forced oscillation of the periodic basic flow and the free oscillation of unstable perturbations of the time-averaged basic flow when the frequency of a free oscillation is half or an integral multiple of the frequency of the forced oscillation (Drazin and Reid 2004). Specially, when the frequency of free oscillation is half that of forced oscillation, the corresponding instability is called as Faraday instability in honor of Faraday who first noted this phenomenon. In the text below, the forced oscillation is mentioned as oscillation for convenience. Lin at al. (1996) investigated the effects of stream-wise oscillation on the long-wave instability. Their analyses showed that the long-wave stability can be completely eliminated by imposing a stream-wise oscillation. Garih et al. (2013) carried out a detailed analysis of the vibration induced instability of a liquid film flow, and found mode competition between parametric instabilities, and a relation between the eigenfunction shape of pressure perturbation and the parametric instability mode.

Because adopting half thickness of the liquid film (Woods and Lin 1995; Lin et al. 1996; Garih et al. 2013), and the oscillation frequency as the units, the dimensionless oscillation frequency is equal to one at all cases, and its effects on the stability are reflected by a combination of other dimensionless parameters. Hence, the effect of oscillation frequency on the stability is still indefinable in the works of (Woods and Lin 1995; Lin et al. 1996; Garih et al. 2013). Woods and Lin (1995) discussed the interaction between shear, long-wave and parametric instabilities, and Garih et al. (2013) discussed mode competition between parametric instabilities. However, their discussion are all limited to linear stage of instabilities. Thus, a numerical investigation of nonlinear interaction of the long-wave and parametric instabilities is still desirable.

Benney (1966) is the first one who gave a nonlinear evolution model called the Benney equation about the local height for the film flow. Benney equation is accurate at small Reynolds numbers, but fails quickly as the Reynolds number is increased. Based on assuming a self-similar velocity profile, Shkadov (1967) proposed an “integral boundary layer model” (IBLM), which comprises two equations about the local film height and flow rate, respectively. This model describes the nonlinear dynamics of the film at moderate Reynolds numbers, but the critical condition for instability is incorrect unless the plane is vertical. By combining the gradient expansion with a “weighted residuals technique” using polynomials as test functions for the velocity field, Ruyer and Manneville (1998) proposed a “weighted residual model” (WRM) which has similar structure with the “integral boundary layer model” proposed by Shkadov. The WRM predicts the correct critical condition for instability and describes satisfactory nonlinear evolution of the film at moderate Reynolds numbers. This is a reasonable consequence of assuming the semi-parabolic velocity profile within the film in the derivation of the WRM. In fact, the velocity profile is near semi-parabolic, and the pressure within the film is near a static pressure distribution at a rather large range of Reynolds numbers, as shown by direct numerical simulation carried out by Salamon et al (1994) The WRM has no limitation on the flow parameters besides the assumption of long-wave disturbance. The perturbation method is applicable to the WRM if the Reynolds number is small enough. After some manipulations, the WRM can be deduced to the Benney equation. Hence, the WRM is applicable to describe nonlinear evolution of the film flow from small to moderate Reynolds numbers.

Oron (Oron and Gottlieb 2002) added a temporal modulation term in the Benney equation to investigate the nonlinear evolution of the film subjects to a stream-wise periodic oscillation. They found that periodic planar boundary excitation does not alter the fundamental unforced bifurcation structure and the spatial topological structure of the interfacial waves. The Benney equation embedded temporal modulation still fails quickly as the Reynolds number is increased. Oron et al. (2009) then derived a WRM embedded temporal modulation to investigate the nonlinear dynamics of film evolution at moderate Reynolds numbers. They found that the combination of traveling wave and non-stationary wave arising in the unmodulated system resulted in the emergence of quasiperiodic and apparently chaotic regimes.

All the works mentioned above focused on the cases of Newtonian fluids. The Orr-Sommerfeld equation and nonlinear models, i.e., the Benney equation, IBLM and WRM have been generalized to the cases of non-Newtonian fluids, and the effects of external oscillation on non-Newtonian fluids have also been studied. Miladinova et al. (2004) derived a Benney-type equation, and Mogilevskii and Shkadov (2010) applied the IBLM to power law fluids. Ruyer-Quil et al. generalized the WRM to the case of power-law fluid and showed the capacity of the generalized WRM in both linear and nonlinear regimes by a convincing agreement in comparison with Orr-Sommerfeld stability analysis and with direct numerical simulation. Mogilevskiy (Mogilevskiy and Vakhitova 2019) applied the IBLM to a power-law fluid subjected to an external high-frequency oscillation, and found that the external oscillation stabilize the flow. The successes in predicting the instability growth rates and describing the nonlinear dynamics of flow for different fluids demonstrate the robustness of these models.

In this paper, based the Floquet theory, the influences of amplitude and frequency of external oscillation as well as the Reynold number on a vertical falling Newtonian liquid film, are examined by a combination of linear stability analyses and nonlinear numerical simulations. An unsteady Orr-Sommerfeld equation with a temporal modulation term governing the linear stability of film is derived from “viscosity-gravity” scaling introduced by Ruyer and Manneville (1998; Kalliadasis et al. 2012). An unsteady WRM embedded a temporal modulation term to describe the nonlinear evolution of oscillation film is derived via using a semi-parabolic velocity profile as the test function in the Galerkin weighted residual method. The unsteady Orr-Sommerfeld equation which has been validated by experiments (Garih et al. 2017) is used to investigate the growth rate of instability. Only the mode competition between long-wave and parametric instabilities from small to moderate Reynolds numbers are concerned here. This implies that the Tollmien-Schlichting wave which only arises at large Reynolds numbers (Burya and Shkadov 2001) is absent here. The unsteady WRM with a temporal modulation term is then verified by convincing agreement in linear analysis comparing with the unsteady Orr-Sommerfeld equation. As pointed out by S. Julius et al. (2019) who made comparison between experiment and three-dimensional numerical simulations, three-dimensionality is not a necessary component in the simulation of the onset and growth of the nonlinear higher modes in film flows. Thus, a two-dimensional unsteady WRM is adequate to describe the generation of parametric instabilities and their competitions.

The novel contributions of the present study are (i) by adopting the “viscosity-gravity” scaling proposed by Ruyer-Quil and Manneville (1998), the control parameters of the problem were reduced to limited ones depending on flow rate and external oscillation amplitude and frequency, facilitating comparison with experiments; (ii) with the “viscosity-gravity” scaling, the influences of oscillation amplitude and frequency on liquid film stability were investigated thoroughly by separating them from other dimensionless parameters, and it was found that either increasing or decreasing oscillation frequency can suppress the long-wave instability; (iii) a weighted residual model was proposed to account for the influence of perpendicular external oscillation, and proven to be capable of predicting the linear stability and nonlinear dynamics of the vertical falling film flow; and (iv) chaotic behavior in flow was captured, which was also observed in the cases where the external oscillation is parallel to the stream-wise direction (Oron et al. 2009).

Formulation

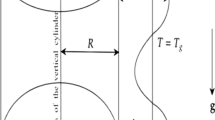
A viscous incompressible Newtonian fluid falling freely under gravity g without disturbance down along a vertical plane that vibrate sinusoidally with a_y sin ωt in the horizontal direction will result in a uniform film flow known as the basic flow, as shown in Fig. 1. The density and viscosity of the thin film are denoted as ρ and μ, respectively, and x, y are the vertical and horizontal direction axis. The coordinate origin is locateed at the plane. The amplitudes of oscillation of the plane with frequency ω at the y axis is a_y. Heat transfer is ignored here, i.e. the wall temperature is assumed to equal to the air temperature.

Fig. 1

Sketch of a thin liquid film of mean film thickness d flowing down a vertical plane that vibrates sinusoidally in the horizontal direction; U(y) is the semi-parabolic velocity profile corresponding to the fully-developed viscous film flow in the absence of external disturbance

Governing Equations and Boundary Conditions

The flow satisfies the continuity equation and the Navier-Stokes equations, the conditions of non-slip, non-penetration at the wall, and the kinematic and dynamic boundary conditions at the free surface. The governing equations are

$$ \left\{\begin{array}{l}\nabla \cdot \mathbf{v}=0\\ {}{\partial}_t\mathbf{v}+\mathbf{v}\cdot \nabla \mathbf{v}=-\frac{\nabla p}{\rho }+\nu {\nabla}^2\mathbf{v}+\mathbf{g}-\mathbf{A}(t)\end{array}\right. $$

(1)

where∇is the gradient operator, ${\nabla}^2={\partial}_x^2+{\partial}_y^2$is the Laplace operator, ${\partial}_x^2,{\partial}_y^2$are the second-order partial derivatives with respect to x, y, ∂_tis the first derivative with respect to t, t is time,v = (u, v)are velocities at the x, y directions, respectively.pis the pressure, νis the kinematics viscosity, andA(t) = (0, A_y) = (0, a_y)ω² sin ωtare the accelerations of oscillation at the x, y directions, respectively.

The boundary conditions at the wall y = 0are

$$ \mathbf{v}\left(x,0,t\right)=0 $$

(2)

The boundary conditions at the free surface y = dare

$$ {\displaystyle \begin{array}{l}{h}_t+\mathbf{v}\cdot \nabla h=v\\ {}\mathbf{T} \cdot \mathbf{n}+\mathbf{n}\sigma \nabla \cdot \mathbf{n}=0\end{array}} $$

(3)

where T is the stress tensor, σ is the surface tension, $\mathbf{n}=\left(-{\partial}_xh,1\right)/\sqrt{1+{\left({\partial}_xh\right)}^2}$is the unit outward normal vector. For a Newtonian fluid, the stress tensor is

$$ \mathbf{T}=-p\mathbf{I}+\mu \left[\nabla \mathbf{v}+{\left(\nabla \mathbf{v}\right)}^{\mathrm{T}}\right] $$

(4)

where I is identity matrix, and superscript T denotes transposition.

Nondimensionalization

Scaling and Dimensionless Numbers

The basic velocity profile of a plat thin film flow without oscillation is

$$ U\left(y,t\right)=\frac{\rho {gd}^2\sin \theta }{2\mu }y\left(2-y\right) $$

(5)

Noted that ρ, μ and g are dimensional-independent parameters, from which we can define more parameters

$$ {\displaystyle \begin{array}{l}{u}_{\nu }={\left(\nu g\sin \theta \right)}^{1/3},\kern1.25em {l}_{\nu }={\left({\nu}^2/g\sin \theta \right)}^{1/3},\kern1.25em {t}_{\nu }={l}_{\nu }/{u}_{\nu }={\left(\nu /{g}^2{\sin}^2\theta \right)}^{1/3}\\ {}{U}_0={gd}^2\sin \theta /2\nu ={d}^2/2{t}_{\nu }{l}_{\nu },\kern1.5em {U}_a=2{U}_0/3={d}^2/3{t}_{\nu }{l}_{\nu}\end{array}} $$

(6)

where U₀ is the velocity of the film at the surface, U_a is the average velocity over the film. This is the so called “viscosity-gravity” scales introduced by Kalliadasis and Ruyer-Quil (Kalliadasis et al. 2012) with which the variables can be nondimensionalized

$$ {\displaystyle \begin{array}{l}\left(x\ast, y\ast \right)=\left(x,y\right)/d,h\ast =h/d,\\ {}\left(u\ast, v\ast \right)=\left(u,v\right)/2{U}_0,t\ast =t2{U}_0/d\\ {}p\ast = pd/2{U}_0\rho {u}_{\nu }{l}_{\nu },\end{array}} $$

(7)

where the variables with stars are dimensionless. When the dimensionless parameters are derived in this paper, the stars will be dropped for simplicity in the following.

With the “viscosity-gravity” scaling, several dimensionless numbers can be introduced

$$ {\displaystyle \begin{array}{l}\mathit{\operatorname{Re}}=\rho {U}_ad/\mu ={gd}^3\sin \theta /3{\nu}^2,\\ {}\varOmega =\omega d/2{U}_0,\kern1.75em {d}_y={a}_y/d,\kern1.75em {A}_y=3{Red}_y{\varOmega}^2,\\ {}\Gamma =\sigma {l}_{\nu }/\rho {\nu}^2,\kern1.75em We=\sigma /\rho {gd}^2\sin \theta =\Gamma /{\left(3\mathit{\operatorname{Re}}\right)}^{2/3}\end{array}} $$

(8)

where Re is the Reynolds numbers which is equal to the flow rate defined as U_ad/ν; Ω is the dimensionless frequency of oscillation, (0, d_y)are the amplitudes of oscillation, (0, A_y) are the dimensionless accelerations, Γ is the Kapitza number measuring the ratio of surface tension to inertia, We is the Weber number which can be obtained by grouping the Kapitza and Reynolds number.

Adoption of the “viscosity-gravity” scaling has several advantages: the Kapitza number depends only on the physical property of liquid and independent of the flow. The variable parameters are the Reynolds number Re (or equivalently the flow rate), amplitude d_y and frequency of oscillation Ω which are independent of the physical property. These make it convenient to discuss separately the influence of each parameter on the stability of the falling film flow and compare the results to the experimental ones.

Dimensionless Governing Equations and Boundary Conditions

Substituting the variables in Exp. (7) into Eq. (1) and boundary conditions Eqs. (2) ~ (4), and ignoring the star, we obtain the dimensionless governing equation and boundary conditions

$$ {\partial}_xu+{\partial}_yv=0 $$

(9)

$$ {\displaystyle \begin{array}{l}3\mathit{\operatorname{Re}}\left({\partial}_tu+u{\partial}_xu+v{\partial}_yu\right)=1-{\partial}_xp+\left({\partial}_x^2u+{\partial}_y^2u\right)\\ {}3\mathit{\operatorname{Re}}\left({\partial}_tv+u{\partial}_xv+v{\partial}_yv\right)=-\cot \theta -{\partial}_yp+\left({\partial}_x^2v+{\partial}_y^2v\right)+{A}_y\cos \left(\Omega t\right)\end{array}} $$

(10)

The boundary conditions representing the no-slip and no-penetration conditions at y = 0 are

$$ u=0,v=0,\kern2em y=0 $$

(11)

The boundary conditions representing the kinematics and stress free conditions at y = 1 are

$$ 2{\partial}_xh\left({\partial}_yv-{\partial}_xu\right)+\left(1-{\left({\partial}_xh\right)}^2\right)\left({\partial}_yu+{\partial}_xv\right)=0,\kern2em y=1 $$

(12)

$$ p=\frac{2}{1+{\left({\partial}_xh\right)}^2}\left[{\left({\partial}_xh\right)}^2{\partial}_xu-{\partial}_xh\left({\partial}_yu+{\partial}_xv\right)+{\partial}_yv\right]-\frac{1}{{\left[1+{\left({\partial}_xh\right)}^2\right]}^{3/2}} We{\partial}_x^2h,y=1 $$

(13)

$$ {\partial}_th+\mathbf{v}\cdot \nabla h=v,\kern2em y=1 $$

(14)

where, ∂_x, ∂_y represent the first order partial derivatives with respect tox, y, and ${\partial}_x^n,{\partial}_y^n$ represent the n-th order partial derivatives with respect tox, y.

Linear Stability Analysis

In the absence of external oscillation, the basic flow is unstable to long-wave perturbations if the Reynolds number or flow rate exceeds a critical value which is determined by the inclined angle and other parameters. The stability of the film under oscillation can be detected by adding small perturbations to the basic flow. The flow is said to be linearly unstable if at least one of the perturbations grows, or linearly stable if all the perturbations decay. Otherwise, the flow is neutrally stable.

Basic Flow

It is easy to verify that an exact solution of the differential system (9)–(14) is given by:

$$ U\left(y,t\right)=\frac{1}{2}y\left(2-y\right)+\mathrm{Real}\left({d}_x\Omega \left({C}_1{\mathrm{e}}^{\alpha_1y}+{C}_2{\mathrm{e}}^{-{\alpha}_1y}-\mathrm{i}\right){\mathrm{e}}^{\mathrm{i}\Omega t}\right) $$

(15)

$$ P(y)=\left(\cot \theta -{A}_y\cos \Omega t\right)\left(1-y\right) $$

(16)

whereC₁ = ie^−α/(e^α + e^−α), C₂ = ie^α/(e^α + e^−α),α = (1 + i)β,$\mathrm{i}=\sqrt{-1}$ is the imaginary unit,$\beta =d/\delta =\sqrt{3\Omega \mathit{\operatorname{Re}}/2}$is the ratio of liquid thickness to the Stokes boundary layer thickness$\delta =\sqrt{2\nu /\omega }$, and operator Real indicates only the real part is considered.

Unsteady Orr-Sommerfeld Equation

After perturbation, each function can be written as a sum of basic state and linear perturbation

$$ u=U\left(y,t\right)+u^{\prime}\left(x,y,t\right),\kern0.75em v=v^{\prime}\left(x,y,t\right),\kern0.75em p=P(y)+p^{\prime}\left(x,y,t\right),\kern1em h=1+h^{\prime } $$

(17)

Substituting the perturbed functions into differential systems (9)–(14), and ignoring the high order terms, one can obtain the linearized differential system for the perturbations. In terms of stream functionψ, the perturbation velocities can be written as

$$ u={\partial}_y\psi, v=-{\partial}_x\psi $$

(18)

Furthermore, all perturbation functions can be written in the form of normal mode solution

$$ \left(\psi, p,h\right)=\left[\phi \left(y,t\right),\hat{p}\left(y,t\right),\hat{h}(t)\right]{\mathrm{e}}^{\mathrm{i} kx} $$

(19)

where k is the wavenumber, $\phi \left(y,t\right),\hat{p}\left(y,t\right),\hat{h}(t)$are the amplitudes of perturbation functions. Substituting each function in the form of normal mode solution into the linearized Navier-Stokes equation results in the unsteady Orr-Sommerfeld equation

$$ 3\mathit{\operatorname{Re}}\left({\partial}_t\left({\partial}_y^2-{k}^2\right)\phi +\mathrm{i}k\left[U\left({\partial}_y^2-{k}^2\right)-{\partial}_y^2U\right]\phi \right)-{\left({\partial}_y^2-{k}^2\right)}^2\phi =0 $$

(20)

By replacing ∂_t with −ick in (20), the steady Orr-Sommerfeld equation is obtained.

Similarly, the linearized boundary conditions for the amplitudes of the perturbation functions are

$$ {\partial}_y\phi =0,\kern4.5em y=0 $$

(21)

$$ \phi =0,\kern4.5em y=0 $$

(22)

$$ \left({\partial}_y^2+{k}^2\right)\phi +{\partial}_y^2U\hat{h}=0,\kern4.5em y=1 $$

(23)

$$ {\displaystyle \begin{array}{l}3\mathit{\operatorname{Re}}\left[{\partial}_{ty}\phi +\mathrm{i}k\left(U{\partial}_y-{\partial}_yU\right)\phi \right]-\left({\partial}_y^3-3{k}^2{\partial}_y\right)\phi \\ {}+\mathrm{i}k\left[\left(\cot \theta -{A}_y\cos \Omega t\right)+{k}^2 We\right]\hat{h}=0,\kern5.5em y=1\end{array}} $$

(24)

$$ \left({\partial}_t+\mathrm{i} k U\right)\hat{h}+\mathrm{i} k\phi =0,\kern4.5em y=1 $$

(25)

The differential system consisting of (20) ~ (25) governs the linear stability of the film flow under temporally periodic oscillation.

Chebyshev Collocation Method and Floquet Theory

With the Chebyshev collocation method (Schmid & Henningson 2001), the differential system consisting of (20) ~ (25) can be written as

$$ 3\mathit{\operatorname{Re}}\left\{\left({q}^2{\mathrm{D}}^2-{k}^2\mathrm{I}\right)\frac{\mathrm{d}\overrightarrow{\phi }}{\mathrm{d}t}+\mathrm{i}k\left[U\left({q}^2{\mathrm{D}}^2-{k}^2\mathrm{I}\right)-{\partial}_y^2U\mathrm{I}\right]\overrightarrow{\phi}\right\}-{\left({q}^2{\mathrm{D}}^2-{k}^2\mathrm{I}\right)}^2\overrightarrow{\phi}=0 $$

(26)

$$ {\phi}_0=0 $$

(27)

$$ q{\mathrm{D}}_{\left(1,1:N+1\right)}\overrightarrow{\phi}=0 $$

(28)

$$ \left({q}^2{\mathrm{D}}_{\left(1,1:N+1\right)}^2+{k}^2\right)\overrightarrow{\phi}+{\partial}_y^2U(1)\hat{h}=0 $$

(29)

$$ {\displaystyle \begin{array}{l}3\mathit{\operatorname{Re}}\left\{q{\mathrm{D}}_{\left(N+1,1:N+1\right)}\frac{\mathrm{d}\overrightarrow{\phi }}{\mathrm{d}t}+\mathrm{i}k\left[U(1)q{\mathrm{D}}_{\left(N+1,1:N+1\right)}-{\partial}_yU(1)\right]\overrightarrow{\phi}\right\}\\ {}-\left({q}^3{\mathrm{D}}_{\left(N+1,1:N+1\right)\Big)}^3-3{k}^2q{\mathrm{D}}_{\left(N+1,1:N+1\right)}\right)\overrightarrow{\phi}+\mathrm{i}k\left[\left(\cot \theta -{A}_y\cos \Omega t\right)+{k}^2 We\right]\hat{h}=0\end{array}} $$

(30)

$$ \left[\frac{\mathrm{d}}{\mathrm{d}t}+\mathrm{i} kU(1)\right]\hat{h}+\mathrm{i}k{\phi}_N=0, $$

(31)

where q = 2, Dis the first-order derivative matrix, Dⁿ, n = 2, 3, 4 is the n–th-order derivative matrix, and I is identity matrix. The size of each matrix is (N + 1) × (N + 1) and the subscripts (1, 1 : N + 1) and (N + 1, 1 : N + 1) of the matrixes indicates that only the first and (N + 1)-th rows of the matrixes are used. $\overrightarrow{\phi}={\left[{\phi}_0,{\phi}_1\cdots {\phi}_N\right]}^{\mathrm{T}}$is the solution vector about ϕ evaluated at N + 1discrete points of computational domain, N is the index of the last discrete point within the computational domain, and $\frac{\mathrm{d}}{\mathrm{d}t}$is the first order derivative with respect to t. Using the Lanzo’s method of approximation (Gottlieb and Orszag 1977), Eq. (26) and boundary conditions (27) ~ (30) together with the kinetic Eq. (31) constitute a dynamic system determining the stability of the oscillating problem.

The system (26) ~ (31) can be written in a compact form

$$ \mathbf{B}\dot{\mathbf{x}}=\mathbf{A}(t)\mathbf{x} $$

(32)

where $\mathbf{x}=\left({\phi}_0,{\phi}_1,\dots, {\phi}_N,\hat{h}\right)$, a “dot” denotes differentiation with respect to t, and B is a constant matrix, A(t) is a periodic matrix with period T = 2π/Ω. According to the Floquet theory, there is a constant matrix R satisfies

$$ \mathbf{S}\left(t+T\right)=\mathbf{RS}(t) $$

(33)

where S is the fundamental solutions matrix satisfying:

$$ \mathbf{B}\dot{\mathbf{S}}=\mathbf{A}(t)\mathbf{S} $$

(34)

Furthermore, if the characteristic roots of R are λ_j(j = 1, N + 2), then, the solution of system (39) can be written as

$$ {\mathbf{x}}_j(t)={\mathrm{e}}^{\mu_jt}{\mathbf{z}}_j(t),\mathrm{with}\ {\mathbf{z}}_j\left(t+T\right)={\mathbf{z}}_j(t) $$

(35)

where μ_jare the so-called characteristic exponents and they are related to the characteristic roots by

$$ {\mu}_j=\frac{1}{T}\ln {\lambda}_j $$

(36)

Thus,

$$ {\mathbf{x}}_j\left(T+t\right)={\mathrm{e}}^{\mu_jT}{\mathbf{x}}_j(t) $$

whereμ_j = (μ_r + iμ_i)_j, with the subscripts r and i representing the real and imaginary parts of μ, respectively. It is clear that(μ_r)_jdetermines whetherx_j(t)grows or not, and the imaginary partμ_igives the oscillation frequency of perturbation, which is also called the free frequency. In particular, the perturbation will decay if none of the characteristic exponents (μ)_j, (j = 1, 2⋯N + 2) have a real part(μ_r)_j > 0, and will grow if at least one of the characteristic exponents satisfies(μ_r)_j > 0. Otherwise, the flow is neutrally stable. Thus, to findμ_j, one must obtainRfirst. Based on Eq. (33) S(T) = RS(0). Letting S(0) be the identity matrix I, yieldsR = S(T). Hence, Rcan be obtained by integrating (34) over one period withS(0) = I.

Our codes have been validated by excellent agreements between our growth rates and that of Woods and Lin (Woods and Lin 1995). Taking the control parameters as: d_y = d_{y, W}/2,Ω = Ω_W/2 sin θRe_WFr_W,${A}_y={d}_{y,W}{\Omega}_W^2/{Fr}_W\sin \theta$,$\mathit{\operatorname{Re}}=8\sin \theta {Fr}_W{\mathit{\operatorname{Re}}}_W^2/3$,We = We_W/4 sin θFr_W, k = 2k_W,μ_W = μ/Ω(where the parameters with subscript W are adopted in Woods and Lin’ paper), the results obtained by Woods and Lin are recovered. Graphical results are omitted here for brevity. The number of the Chebyshev collocation points is determined by the control parameters and can be obtained by successively increasing the number until no further improvements in accuracy are observed. It is noted that the oscillation frequency can be expressed by a combination of Reynolds number and Froude number used by Woods and Lin, i.e., Ω = 1/2 sin θRe_WFr_W. This implies that either a change of Reynolds number or Froude number will result in a change of the oscillation frequency. Thus, the effect of oscillation frequency on the stability is indefinable because the frequency cannot vary independently.

Results

A vertical falling liquid film is always unstable to long-wave disturbances. An imposition of external oscillation on the film can suppress the long-wave instability, whilst causing parametric instabilities. The influence of oscillation on the long-wave and parametric instabilities under various parameters will be investigated in detail in the following sections. Only water is considered. Therefore, in the results to be presented in the following sections, Γ = 3375.

Influence of Oscillation Amplitude

Parametric instabilities are caused by oscillation, the parameters measuring oscillation are oscillation amplitude and frequency. The influence of oscillation amplitude d_y is covered by acceleration A_y which appears only in equation for the normal stress boundary condition. The influence of oscillation is removed by taking d_y = 0. The effect of oscillation amplitude on the stability can be investigated separately by holding other parameters fixed.

Figures 2 and 3 show the dispersion relations for different oscillation amplitudes. Figure 2 shows an increase of suppression on the long-wave instability by an increase of oscillation amplitude. Figure 3 shows that an increase of oscillation amplitude results in larger growth rate, wider unstable wavenumber range and more unstable modes. For example, there are seven crests on the curve labeled d_y = 5, corresponding to seven modes, among which six modes are unstable (here for convenience, the unstable modes are the first through the sixth according to their wavenumber ranges). It is seen from Fig. 3a that the maximum growth rate of the second mode exceeds that of the first mode as the oscillation amplitude is increased. As the oscillation amplitude increases further, the maximum growth rate of the third mode exceeds that of the second mode. The Fig. 3 also shows that the increase of oscillation amplitude has only a little effect on the most dangerous wavenumber. It is seen from Fig. 2 that the most dangerous wavenumber is aboutk_m = 0.7in the absence of oscillation, and the most unstable wavenumber is aboutk_m = 0.07in the presence of oscillation. This indicates that the parametric instability has a much shorter wavelength compared with the long-wave instability.

Fig. 2

Effect of varying oscillation amplitude on long-wave instability: Re = 5, Ω = 5

Fig. 3

Effect of varying oscillation amplitude on parametric instability: Re = 5, Ω = 5

Figure 4 displays the neutrally stable curves on the(k, d_y)plane, where these curves separate this plane into stable and unstable regions which are denoted by S and U, respectively. The solid line represents the neutrally stable curve for the long-wave instability. An increase of oscillation amplitude results in a narrower and narrower unstable region for long-wave instability, and wider and wider unstable regions for parametric instabilities. This indicates that increase of oscillation amplitude with other parameters fixed results in suppression of the long-wave instability and enhancement of the parametric instabilities.

Fig. 4

Neutrally stable curves on the (k, d_y) plane. S represents the stable region, U represents the unstable region, and the solid line represents the neutrally stable curve for the long-wave instability in the absence of oscillation with: Re = 5, Ω = 5

Influence of Oscillation Frequency

The oscillation frequency is not only present explicitly in the equation of normal stress boundary condition, but also acts implicitly in the time dependent terms of other equations. The effect of varying oscillation frequency on the stability of film cannot be covered fully by the oscillation acceleration, and can be investigated by holding the oscillation acceleration fixed or holding the oscillation amplitude fixed.

Figure 5 gives the dispersion relations for different frequencies with the acceleration fixed. It is seen from Fig. 5a that increase of oscillation frequency results in decrease of suppression of the long-wave instability. This suppression is close to zero as the frequency is increased. Figure 5b shows that there is a critical frequency Ω_cri where the growth rate achieves its maximal value when the acceleration is fixed. Ω_cri ≈ 6 for the parameters used in the caption in Fig. 5. IfΩ > Ω_cri, an increase of oscillation frequency results in a larger most dangerous wavenumber, a narrower range of unstable wavenumbers, less unstable modes, and a lower maximal growth rate. On the contrary, ifΩ < Ω_cri, a decrease of oscillation frequency will result in a smaller most dangerous wavenumber, a wider range of unstable wavenumbers, more unstable modes lower, but a lower maximal growth rate. Figure 6 gives the neutrally stable curves on the (k, Ω)plane, where S represents stable region, U unstable region. The unstable region for parametric instabilities becomes narrower and narrower, and the unstable region for long-wave instability become wider and wider, as the frequency is increased. This indicates increasing oscillation frequency with acceleration fixed tends to stabilize the parametric instability and weaken its stabilizing effecting on the long-wave instability.

Fig. 5

Influence of varying frequency on the stability:Re = 5, A_y = 500

Fig. 6

Neutrally stable curves on the(k, Ω)plane, where S represents stable region, U unstable region, and solid line represents neutrally stable curve for the long-wave stability in the absence of oscillation: Re = 5, A_y = 500

The influence of varying oscillation frequency with oscillation amplitude fixed is then investigated, as shown in Figs. 7 and 8. It is clear that the effect of increasing oscillation frequency with oscillation amplitude fixed is in favor of suppression of the long-wave instability and enhancement of the parametric instability.

Fig. 7

Influence of varying oscillation frequency on the stability with the oscillation amplitude fixed with: Re = 5, d_y = 1

Fig. 8

Neutrally stable curves on the(k, Ω)plane where S represents the stable region, U stable region, and solid line the neutral curve for long-wave instability in the absence of oscillation: Re = 5, d_y = 1

A comparison between Figs. 6 and 8 demonstrates that a decrease of oscillation frequency with acceleration fixed is in favor of suppression of the long-wave instability (see Fig. 6), and an increase of oscillation frequency with oscillation amplitude fixed is also in favor of suppression of the long-wave instability (see Fig. 8). Hence, either decreasing or increasing oscillation frequency can suppress the long-wave instability. The difference between them is that the acceleration is fixed in the formal case, and the oscillation amplitude is fixed in the latter case. Similar conclusion can be drawn for the parametric instabilities. That is, either increasing or decreasing oscillation frequency can suppress the parametric instabilities, depending either the oscillation acceleration or amplitude is fixed.

The long-wave and parametric instabilities compete with each other as the oscillation frequency or amplitude is varied. A suppression of the long-wave instability always accompanies enhancements of the parametric instabilities, and vice versa.

Influence of the Reynolds Number

Figure 9 gives dispersion relations for various Reynolds numbers. It is seen from Fig. 9a that the long-wave instability is always suppressed by oscillation for all Reynolds numbers. An increase of the Reynolds number results in an increase of the suppression, which is also indicated by Fig. 10 which gives the neutrally stable curves on the (k, Re) plane. It is seen from Fig. 9b that the maximal growth rate of the second mode may exceed that of the first mode as the Reynolds number is increased. An increase of Reynolds number results in a wider range of unstable wavenumbers and more unstable modes. This is also clear in Fig. 10. Both the long-wave and parametric instabilities become stronger and stronger, and the mode competition between them is absent, as the Reynolds number is increased.

Fig. 9

Influence of varying Reynolds number on the stability: d_y = 1, .Ω = 6.

Fig. 10

Neutrally stable curves on (k, Re) plane where S represents stable region, U unstable region, and solid line the neutrally stable curve for long-wave instability in the absence of oscillation: d_y = 1, .Ω = 6

Nonlinear Numerical Simulations

Nonlinear numerical simulation is used to describe nonlinear evolution of thin film flow, which exceeds capacity of linear stability analysis which is efficient in predicting the most unstable wavenumber, growth rate, free oscillation frequency, and critical condition for instability.

Weighted Residual Model

The ratio of film thickness d to characteristic length l of the flow is always a small parameter, i.e., ε = d/l ≪ 1, if l is the characteristic length of stream-wise direction. Correspondingly, the scale for velocity v is taken asεd²/t_υl_υ.

Following Kalliadasis et al. (2012), using u = y/h − y²/2h²as the test function and applying Galerkin weighted residual method, we obtain a “simplified second-order model” incorporated with a temporal modulation term:

$$ {\displaystyle \begin{array}{l}{\partial}_th=-{\partial}_xq\\ {}3\varepsilon \mathit{\operatorname{Re}}{\partial}_tq=\frac{5}{6}h-\frac{5}{2}\frac{q}{h^2}-3\varepsilon \mathit{\operatorname{Re}}\left(\frac{17}{7}\frac{q}{h}{\partial}_xq-\frac{9}{7}\frac{q^2}{h^2}{\partial}_xh\right)\\ {}-\varepsilon \left[\cot \theta -{A}_y\cos \left(\Omega {\varepsilon}^{-1}t\right)\right]\frac{5}{6}h{\partial}_xh+\frac{5}{6}h{\partial}_x^3h\\ {}+{\varepsilon}^2\left[4\frac{q}{h^2}{\left({\partial}_xh\right)}^2-\frac{9}{2h}{\partial}_xq{\partial}_xh-6\frac{q}{h}{\partial}_x^2h+\frac{9}{2}{\partial}_x^2q\right]\end{array}} $$

(37)

where A_y cos(Ωε⁻¹t)(h − y)represents the temporal modulation perpendicular to the plane. When it is removed, the “simplified-second-order model” proposed by Kalliadasis et al. (2012) is recovered. The model (37) is called as weighted residual model (WRM) for simplicity in following sections.

The WRM has two shortcomings. First, it is applicable only if the Weber number is sufficiently large. Second, it is applicable only to cases where the velocity profiles in the film do not depart too much from the semi-parabolic profile. This is limited by the assumption adopted in the derivation of the WRM. Since the Kapitza number is taken as 3375 in this paper, the Weber number is always not too small for typical film flows. Thus, the WRM is still valid if the film is not very thin, such ash < 10⁻³. It is noted that the WRM is exact if the Reynolds number tends to zeros, because it is equivalent to the Benney equation which is exact in that situation.

The WRM has two advantages over the Navier-Stokes equation. It is much easier to solve because the transverse momentum equation has been integrated by applying long-wave assumption. It even predicts a more accurate evolution of local film height compared with numerical simulations with a combination of the Navier-Stokes equations and an interface tracking method such as VOF (Gao et al. 2003) because the latter usually suffers from errors introduced in dealing with the surface tension.

Mathieu Equation

The WRM can be validated by comparison with the unsteady Orr-Sommerfeld equation in prediction of linear stability. By linearizing the equations around the temporally periodic undisturbed solution$h={h}_N=1,q={q}_N={h}_N^3/3=1/3$, and writing the linear perturbationsh^', q^'in the normal formal

$$ {h}^{\hbox{'}}={\mathrm{e}}^{\mathrm{i} kx}\varphi (t),\kern1em {q}^{\hbox{'}}={\mathrm{e}}^{\mathrm{i} kx}\chi (t) $$

We obtain the equation for perturbation amplitudes of h, derived from the linear version of Eq. (37):

$$ 3\varepsilon \mathit{\operatorname{Re}}\frac{{\mathrm{d}}^2\varphi }{\mathrm{d}{t}^2}+b(t)\frac{\mathrm{d}\varphi }{\mathrm{d}t}+c(t)\varphi =0 $$

(38)

where $\frac{\mathrm{d}}{\mathrm{d}t},\frac{{\mathrm{d}}^2}{\mathrm{d}{t}^2}$represent the first and second-order derivatives respect to t, respectively, and

$$ {\displaystyle \begin{array}{l}b(t)=\left(\frac{51}{7}\mathrm{i} k\varepsilon {Req}_N(t)+\frac{9}{2}{\varepsilon}^2{k}^2+\frac{5}{2}\right)\\ {}c(t)=\left(\begin{array}{l}-\frac{27}{7}\varepsilon {Rek}^2{q}_N^2(t)-6\mathrm{i} k\varepsilon \mathit{\operatorname{Re}}{\dot{q}}_N(t)+6\mathrm{i}{\varepsilon}^2{k}^3{q}_N(t)\\ {}+\frac{5}{6}\varepsilon {k}^2\left(\mathit{\cot}\theta -{A}_y\cos \left(\Omega {\varepsilon}^{-1}t\right)\right)+\frac{5}{6}{k}^4+\frac{5}{2}\mathrm{i}k\end{array}\right)\end{array}} $$

Equation (38) is a second-order ordinary differential equation with periodic coefficients. It is a Mathieu type equation. It is a simplification of the unsteady system (32), and it determines the stability of temporally periodic undisturbed solution of the WRM (37). It can be written in the form of two ordinary differential equations of first-order and integrated with the same method used in system (34). The stability of the film is determined by the Floquet exponentμ, as we have shown before.

Validation

Figure 11 gives comparisons between the Mathieu equation and O-S equation in predicting the neutrally stable curves. It is clear that the Mathieu equation is very accurate in predicting the neutrally stable curves ifd_y ≤ 5, 1 ≤ Ω ≤ 10, Re  ≤ 10. Hence, the WRM is valid if the Reynolds number, oscillation amplitude and frequency are not very large. In the following, the nonlinear evolutions of film flow will be investigated in the validity domain of the WRM.

Fig. 11

Comparisons between the weighted residual model and O-S equation: (a) Re = 5, Ω = 5,(b) Re = 5, A_y = 500, (c) Re = 5, d_y = 1, (d) Ω = 6, d_y = 1

Discussions

In this section, we pose a series of initial-value problems that probe the nonlinear evolutions of the film flow. Initial-value problems correspond to the temporal linear stability analyses as we have adopted. Periodic boundary conditions are applied in the spatial direction and the Fourier spectral method are used to approximate the spatial derivatives for temporal numerical simulations. Time advancing is achieved by a Gear method. The results from linear analysis is used to initialize and validate the simulation with the WRM.

Figure 12 displays the linear growth rate and oscillation frequency of perturbation as functions of wavenumbers for parametersRe = 5,Ω = 6, d_y = 0.5. Each parametric instability mode corresponds to a slow change of oscillation frequency of perturbation. The linear analysis predicts a most unstable wavenumberk_m = 0.75and the corresponding oscillation frequency of perturbation μ_i = 0.45Ω. Noted that the normal solution can be rewritten asx(t) = e^μtz(t) = e^{(μ + inΩ)t}[e^−inΩtz(t)], n = 0, ± (1, 2⋯). This implies that both μ_i and μ_i + nΩ are frequencies of periodic solutions. Sinceμ_i = 0.45Ωis the frequency of one periodic solution, then μ_i = (0.45 ± 1)Ωare the frequencies of another two periodic solutions. Similarly,μ_i = (0.075 ± 1)Ω and so on, are the frequencies of periodic solutions. Only the absolute values of oscillation frequencies of perturbations are present here, as shown in Fig. 12b. Substituting μ = iμ_i = i0.5Ωinto$h=\hat{h}(t){\mathrm{e}}^{\mathrm{i} kx}={\mathrm{e}}^{\mu t}z(t){\mathrm{e}}^{\mathrm{i} kx}$, we have $h\left(x,2T+t\right)=\hat{h}\left(2T+t\right){\mathrm{e}}^{\mathrm{i} kx}=\hat{h}(t){\mathrm{e}}^{\mathrm{i} kx}=h\left(x,t\right)$. This implies the unstable wave is a Faraday wave. Similarly, takingμ = iμ_i = i0.45Ω, we $h\left(x,2T+t\right)=\hat{h}\left(t+2T\right){\mathrm{e}}^{\mathrm{i} kx}=\hat{h}(t){\mathrm{e}}^{\mathrm{i}\left( kx-0.1\Omega T\right)}=\hat{h}(t){\mathrm{e}}^{\mathrm{i}2\pi \left(x/L-0.1\right)}$. This implies that h is a traveling Faraday wave with phase velocity0.05Ω/k, and there is a phase difference of 0.1 times wavelength between two successive wave shapes. This phase velocity is due to the falling flow of the film. In fact, if the falling flow is ignored, i.e. U_a = 0, then, μ_i = 0.5Ω and the phase velocity is zero.

Fig. 12

The growth rate and oscillation frequency of perturbation versus wavenumber with parameters (Re = 5, Ω = 6, d_y = 0.5): (a) The growth rate, (b) the oscillation frequency of perturbation

Takingk = k_m/10 = 0.075as the wavenumber in computational space, carrying out a simulation with the WRM initiated withh = 1 + 0.1 cos kx, q = 1/3, we can obtain snapshots for the evolution of film. Figure 13 gives the wave shapes at two different time nodes. At the initial time, the computational box contains one wavelength. After an evolution of sufficient long time, such as 65 wave period T, the computational box contains ten shorter wavelengths. This indicates a most unstable numberk = 0.075 × 10 = k_m. This is consistent with prediction of the linear stability analysis.

Fig. 13

The most dangerous mode:Re = 5, Ω = 6, d_y = 0.5, k = 0.075, L = 2π/k

Figure 14 shows snapshots of a set of sequential wave shapes at different time nodes with time interval T. It should be noted that only one wavelength is contained in the computational box, and t = 0is a reference time, not the initial moment. It is seen from Fig. 14a that the unstable free oscillating wave is a traveling Faraday wave with a constant phase velocity. Figure 14b shows comparison of the wave shapesh(x, t) andh(x/L + 0.1, 2T + t). It is seen that the phase difference given by the nonlinear numerical simulation is to close to the one given by linear stability analysis. However, there is still a little a difference in phase difference which is caused by nonlinearity of the wave and this phase difference increases with the nonlinearity.

Fig. 14

Wave shapes at different time nodes: the parameters are given in Fig. 13

Figure 15 displays the corresponding power spectrum as function of oscillation frequency of perturbation for time series of local film height sampled from the simulation considered in Fig. 12. The power spectrum is defined as $P\left(\Omega \right)=F\overline{F}/ NL$. Here, Fis the Fast Fourier Transform (FFT) of time series of local film height,$\overline{F}$is the complex conjugate of F, and NL is the length of the time series. One long-wave mode and four modes of parametric instability can be seen in Fig. 15, and the dominate mode is the Faraday instability, which frequencies areμ_i = |0.45 ± 1|Ω. This is consistent with the prediction given by the linear analysis, as shown in Fig. 12b. Therefore, the WRM is adequate to describing the generation and competition between different parametric instability modes predicted by linear stability analysis.

Fig. 15

Power spectrum versus oscillation frequency of perturbation for time series of local film height for parameters shown in Fig. 12

Figure 16 shows the maximal and minimum film heights as functions of the acceleration which varies temporally periodic ascos(Ωε⁻¹t). h_max, h_minrepresent the maximal and minimum film height, respectively. The smallerh_minis, the closer the film is to rupturing. It is seen from Fig. 16 that the maximal film height during one period increases with the oscillation amplitude. However, when the oscillation amplitude is increased to d_y = 1.75, the evolution curves are close to that of the case withd_y = 2. An increase of d_y results in a complex dynamics, which can be seen from Fig. 16. Asd_y is increased further to 2.5, chaotic behavior emerges, and an accurate long-time prediction becomes impossible. This will be demonstrated later.

Fig. 16

Influence of varying oscillation amplitude on the evolution of the film height with:Re = 5, Ω = 6, (a)d_y = 0.5, k_m = 0.74, (b) d_y = 1, k_m = 0.75, (c) d_y = 1.25, k_m = 0.75, (d) d_y = 1.5, k_m = 0.75, (e) d_y = 1.75, k_m = 0.75, (f) d_y = 2, k_m = 0.74.

Figure 17 shows h_max − h_min and h_min as functions of cos(Ωε⁻¹t).h_max − h_min represents the wave amplitude of the film and measure the nonlinearity of the film flow, and h_minmeasures how close the film is to rupture. As the oscillation amplitude increases, h_max − h_minbecomes larger and larger, and h_min becomes smaller and smaller, which can be seen from (Fig. 17a and b), respectively. Thus, an increase of oscillation amplitude may lead to rupture of the film, and makes the WRM invalid. Within the validity domain of the WRM, both the wave amplitude and the minimal local height of the film are proportional to the oscillation amplitude. This is consistent with the linear analyses which state that both the linear growth rate and unstable wavenumbers range are proportional to the oscillation amplitude (see Figs. 3 and 4).

Fig. 17

Influence of varying oscillation amplitude on the evolution of the film height:Re = 5, Ω = 6, k_m = 0.75, (a) h_max − h_min, (b) h_min

Similar conclusions can also be drawn from investigation of influences of varying frequency with oscillation amplitude fixed (see Fig. 18) and Reynolds number (see Fig. 19) on the nonlinear evolutions of the film, i.e., a larger oscillation frequency or Reynolds number yields in a larger h_max − h_minand a smallerh_min. These are consistent with the linear analyses which state that both the linear growth rate and unstable wavenumbers range are proportional to the oscillation frequency (see Figs. 8 and 9) and Reynolds number (see Fig. 10 and 11).

Fig. 18

Influence of varying frequency with oscillation amplitude fixed on the nonlinear evolution of the film:Re = 5, d_y = 1, (a) h_max − h_min, (b) h_min

Fig. 19

Influence of varying Reynolds number on the nonlinear evolution of the film: d_y = 1, Ω = 6, (a) h_max − h_min, (b) h_min

Figure 20 shows the effects of varying oscillation frequency with acceleration fixed on the h_max − h_min andh_min. Both h_max − h_minandh_minincrease with decrease of oscillation frequency. Increase of oscillation frequency with acceleration fixed has a stabilizing effect on the parametric instability. This is consistent with the prediction from the neutrally stable condition given by Fig. 7 which shows that the unstable region becomes narrower and narrower as the oscillation frequency increases. However, it is not consistent with the growth rate curves given by Fig. 6 which shows that the growth rate achieves its maximum at Ω ≈ 6. Hence, it seems reasonable to believe that a wider unstable wavenumber range indicates a stronger nonlinearity represented by h_max − h_minandh_min.

Fig. 20

Influence of varying frequency with acceleration fixed on the nonlinear evolution of the film: Re = 5, A_y = 500, (a) h_max − h_min, (b) h_min

According to the research carried out by Oron et al. (2009), a forced oscillation parallel to the stream-wise direction of the film flow can lead to a chaotic behavior in the film. Our research shows that a forced oscillation perpendicular to the film can also give rise to a chaotic behavior in the film.

Figure 21 displays the wave shape and phase plane(h, ∂_xh)at a representative time node. Each point in Fig. 21a, b is in a one to one correspondence. Figure 22 displays the phase plane and the Poincaré map calculated with the parameters given in Fig. 21. Eighty one time nodes are contained in Fig. 22a, and the time interval between two sequential time nodes is2T. Since the flow is periodic with period equal to2T, the phase planes at different time nodes with time interval2T are very close except for a phase difference due to falling flow of the film. Figure 22b displays the Poincaré map for periodic solution$\left(h(t),{\partial}_xh(t),{\partial}_x^2h(t)\right)$on the Poincaré section through the point of solution at a reference time node. The Poincaré map, named after Henri Poincaré, is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower-dimensional subspace, called the Poincaré section, transversal to the flow of the system. The discrete points on the Poincaré section forming a closed curve rather than a fixed point, indicates a quasi-periodic motion rather than a periodic motion. This quasi-periodicity behavior is caused by falling flow of the film.

Fig. 21

Waves and phase plane:Re = 5, Ω = 6, d_y = 2. (a)Wave shape, (b) Phase plane of(h, ∂_xh)

Fig. 22

The phase plane and Poincaré map with time series sampled with time interval2T: t₀, t₀ + 2T, t₀ + 4T, t₀ + 6T⋯t₀ + 160T. (a) Phase plane at 81 time nodes, (b) Poincaré map for periodic solution on the Poincaré section through the point of solution at a reference time pointt₀. The parameters given in the caption of Fig. 21

Figure 23 gives the oscillation frequency of perturbation as function of wavenumber predicted by linear stability analysis, and the power spectrum of time series of local film height sampled from numerical simulation for parameters given in Fig. 22. Noted that only the absolute values of frequency is present in Fig. 23a. Four frequencies are present in Fig. 23a, i.e., μ_i = (0.45, 0.075, 0.4, 0.12)Ω. This implies that μ_i = (1.45, 2.45, 0.55, 1.55, 2.551.075, 2.075, 0.925, 1.925, 1.4, 2.4, 1.6, 2.6, 1.12, 2.12, 0.88, 1.88)Ωare also frequencies of the periodic solutions. It is clear that the WRM predicts all the parametric instability modes even if the oscillation amplitude is increased tod_y = 2.

Fig. 23

Oscillation frequency of perturbation versus wavenumber and power spectrum of time series of local film height for parameters given in Fig. 22

Figure 24 displays the phase plane and Poincaré map calculated with the oscillating amplitude being increased to d_y = 2.5and other parameters fixed, i.e.,Re = 5, Ω = 6, d_y = 2.5. The behavior of phase trajectory shown in Fig. 24a is quite different from that in Fig. 22a, and the points on the Poincaré section are irregular, as shown in Fig. 24b. This implies that the flow is chaotic. Thus, it is clear that imposition of an external perpendicular oscillation can induce chaotic behavior in a vertical falling liquid film flow, similar to what happens in the case where the external oscillation is parallel to the stream-wise direction of the film flow. Figure 25 shows that the presence of chaos does not change the power spectrum structure which shows that the Faraday wave mode is the dominate one in the nonlinear evolution of the film flow.

Fig. 24

The phase plane and Poincaré map with time series sampled with time interval2T: t₀, t₀ + 2T, t₀ + 4T, t₀ + 6T⋯t₀ + 160T, and the parameters are:Re = 5, Ω = 6, d_y = 2.5. (a) Phase plane at 81 time nodes, (b) Poincaré map for periodic solution on the Poincaré section through the point of solution at a reference time nodet₀

Fig. 25

Oscillation frequency of perturbation versus wave number and power spectrum for time series of local film height for parameters given in Fig. 24

Chaos is a typical nonlinear dynamic phenomenon, and it arises if the nonlinearity of nonlinear system is strong enough. For the problem considered here, chaotic behavior also arises from increase of the Reynolds number, increase or decrease of oscillation frequency, which yield larger wave amplitudes of the film flow. For the parameters given in Fig. 17, i.e., d_y = 1, Ω = 6, chaos arises if the Reynolds number is increased to Re = 12. However, the WRM is not very accurate in this situation, as shown in Fig. 11d.

Conclusions

Falling liquid film flow has a wide range of applications. There are several instabilities in falling film flow, which are either welcome or undesirable, depending on their applications. Imposing external oscillation is an important method to control the instabilities. Oscillations can suppress long-wave instability, but at the same time introduce parametric instabilities in film flow. By adopting the “viscosity-gravity” scaling, the control parameters of the problem are reduced to the ones that depend only on the flow rate, oscillation amplitude and frequency. Then, the influences of oscillation amplitude and frequency on the stability can be investigated exhaustively by separating them from each other.

The influences of external oscillation on a vertical falling liquid film are then investigated by a combination of linear stability analyses with the unsteady Orr-Sommerfeld equation based on Floquet theory and nonlinear numerical simulations with weighted residual model in this paper. The linear analyses show that increase of oscillation amplitude with other parameters fixed always results in suppression of the long-wave instability and enhancements of the parametric instabilities. On the other hand, either increasing or decreasing oscillation frequency can suppress the long-wave instability and enhance the parametric instabilities, depending on either the oscillation amplitude or the acceleration is fixed. For a given Reynolds number, the long-wave instability and parametric instabilities compete with each other as the oscillating amplitude and frequency are varied. A weakness of the long-wave instability always accompanies enhancements of the parametric instabilities, vice versa. As a contrast, both the long-wave and parametric instability become stronger and stronger when the Reynolds number increases more and more, all the while mode competition between them is absent.

A weighted residual model (WRM) embedded a temporal modulation term is then derived to investigate the nonlinear evolution of the film flow. This model is validated by excellent agreements with the Orr-Sommerfeld equation in predicting the neutrally stable curves. And its capacity in describing the nonlinear dynamics of the falling liquid film flow is demonstrated by a good agreement with the Orr-Sommerfeld equation in predicting the generations and mode competition of parametric instabilities. The numerical simulations show that both the wave amplitudes and minimal local heights of the film are proportional to the unstable wavenumbers ranges rather than the growth rates predicted by linear analyses, i.e., a larger unstable wavenumbers range indicates a larger wave amplitude and a minimal local thickness of the liquid film. The numerical simulations also show that, when the critical conditions are met, imposition of an external oscillation perpendicular to the steam-wise direction of the film can trigger a chaotic behavior in the film, similar to what happens in the case where the oscillation is parallel to the stream-wise direction of the film.