Influence of Gravity on the Stability of Evaporative Convection Regimes

Abstract

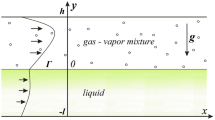
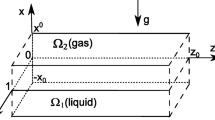
The characteristics of convective regimes in a two-layer system have been investigated in the framework of the Boussinesq approximation of the Navier–Stokes equations. An exact invariant solution of the convection equations is used to describe a joint stationary flow of an evaporating liquid and a gas-vapor mixture in a horizontal channel. Thermodiffusion effects in the gas-vapor phase are additionally taken into account in the governing equations and interface conditions. The influence of gravity and thickness of the liquid layer on the hydrodynamical, thermal and concentration characteristics of the regimes has been investigated. Flows of the pure thermocapillary, mixed and Poiseuille’s types are specified for different values of the problem parameters. The linear stability of the evaporative convection regimes has been studied. The types and properties of the arising perturbations have been investigated and the critical characteristics of the stability have been obtained. Disturbances can lead to the formation of deformed convective cells, vortex and thermocapillary structures. The change of the instability types and threshold thermal loads occurs with the increasing thickness of the liquid layer and gravity action.

Appendix

Unknown Function Form

Distributions of the velocity, temperature and pressure in the liquid layer are defined by the following formulae:

$$u_{1} = \frac{y^{4}}{24}\frac{g {\beta}_{1} {a^{1}_{2}}}{\nu_{1}} +\frac{y^{3}}{6} \frac{g {\beta}_{1} A}{\nu_{1}} + \frac{y^{2}}{2} c_{1} +y c_{2} + c_{3}, $$

$$T_{1} = (A + {a^{1}_{2}} y) x+ \frac{ y^{7}}{1008} \left\{ \frac{g {\beta}_{1} ({a^{1}_{2}})^{2}}{ \nu_{1} \chi_{1}} \right\} +\frac{y^{6}}{144} \left\{\frac{g {\beta}_{1} A {a^{1}_{2}}}{ \nu_{1} \chi_{1}} \right\} + $$

$$+\frac{y^{5}}{120} \frac{1}{\chi_{1}} \left\{\frac{g {\beta}_{1} (A)^{2}}{ \nu_{1} } + 3 {a^{1}_{2}} c_{1} \right\} + \frac{y^{4} }{24} \frac{1}{\chi_{1}} \{ A c_{1} + 2 {a^{1}_{2}} c_{2}\} + $$

$$+\frac{y^{3} }{6} \frac{1}{\chi_{1}} \{A c_{2} + {a^{1}_{2}} c_{3} \} + \frac{y^{2}}{2} \frac{ A}{\chi_{1}} c_{3}+ y\, c_{4} + c_{5}, $$

$$p^{\prime}_{1} = \left( \frac{y^{2}}{2}\rho_{1}g {\beta}_{1} {a^{1}_{2}} + y\rho_{1}g {\beta}_{1} A +\nu_{1}\rho_{1} c_{1} \right)x+ \frac{y^{8}}{8}k_{7} + $$

$$+ \frac{y^{7}}{7}k_{6}+\frac{y^{6}}{6}k_{5}+ \frac{y^{5}}{5}k_{4}+\frac{y^{4}}{4}k_{3} +\frac{y^{3}}{3}k_{2}+ \frac{y^{2}}{2}k_{1}+ yk_{0}+c_{8}. $$

The coefficients, which do not depend on y, are the following:

$$k_{7}=\frac{1}{1008}(g {\beta}_{1} {a_{2}^{1}})^{2} \frac{\rho_{1}}{ \nu_{1} \chi_{1}},\;\; k_{6}=\frac{1}{144}(g {\beta}_{1})^{2} \frac{\rho_{1}}{ \nu_{1} \chi_{1}} {a^{1}_{2}} A, $$

$$k_{5}=\frac{1}{120} \frac{g \rho_{1} {\beta}_{1}}{\chi_{1}} \left( \frac{g {\beta}_{1} (A)^{2}}{ \nu_{1} } + 3 {a^{1}_{2}} c_{1} \right), $$

$$k_{4}=\frac{1}{24} \frac{g \rho_{1} {\beta}_{1}}{\chi_{1}}(A c_{1} + 2 {a^{1}_{2}} c_{2}), $$

$$k_{3}=\frac{1}{6} \frac{g \rho_{1} {\beta}_{1}}{\chi_{1}}(A c_{2} + {a^{1}_{2}} c_{3}),\;\; k_{2}=\frac{1}{2} \frac{g \rho_{1} {\beta}_{1}}{\chi_{1}} A c_{3}, $$

$$k_{1}=g\rho_{1}{\beta}_{1}c_{4},\;\; k_{0}=g\rho_{1}{\beta}_{1} c_{5}. $$

The distributions of the velocity, temperature, pressure and vapor concentration in the upper layer are given by the following expressions:

$$u_{2} \,=\, \frac{y^{4}}{24} \frac{g}{\nu_{2}}({\beta}_{2} {a^{2}_{2}}+{\gamma} b_{2})+ \frac{y^{3}}{6} \frac{g}{\nu_{2}}({\beta}_{2} A +{\gamma} b_{1})+ \frac{y^{2}}{2} \overline{c}_{1} + y \overline{c}_{2} + \overline{c}_{3}, $$

$$T_{2} = (A + {a_{2}^{2}} y) x + \frac{y^{7}}{1008} B_{2} \frac{g}{\nu_{2}} ({\beta}_{2} {a^{2}_{2}}+{\gamma} b_{2}) + $$

$$+\frac{y^{6}}{720} \left[B_{1} \frac{g}{\nu_{2}} ({\beta}_{2} {a^{2}_{2}}+{\gamma} b_{2}) + 4 B_{2} \frac{g}{\nu_{2}} ({\beta}_{2} A +{\gamma} b_{1}) \right] + $$

$$+ \frac{y^{5}}{120} \left[B_{1} \frac{g}{\nu_{2}} ({\beta}_{2} A +{\gamma} b_{1}) + 3 B_{2} \overline{c}_{1} \right] + \frac{y^{4}}{24} [B_{1} \overline{c}_{1} + 2 B_{2} \overline{c}_{2}] + $$

$$+ \frac{y^{3}}{6} [B_{1} \overline{c}_{2} + B_{2} \overline{c}_{3}] + \frac{y^{2}}{2} B_{1} \overline{c}_{3} + y \overline{c}_{4} + \overline{c}_{5}, $$

$$p^{\prime}_{2}= \left[ \frac{y^{2}}{2} (\rho_{2}g {\beta}_{2} {a^{2}_{2}} +\rho_{2}g {\gamma} b_{2}) + y (\rho_{2}g {\beta}_{2} A + \rho_{2}g {\gamma} b_{1}) +\right. $$

$$\left.+\rho_{2} \nu_{2} \overline{c}_{1} \right]x+\frac{y^{8}}{8} \overline{k}_{7}+\frac{y^{7}}{7}\overline{k}_{6}+ \frac{y^{6}}{6}\overline{k}_{5}+ \frac{y^{5}}{5}\overline{k}_{4}+ $$

$$+\frac{y^{4}}{4}\overline{k}_{3}+ \frac{y^{3}}{3}\overline{k}_{2}+\frac{y^{2}}{2}\overline{k}_{1} +y\overline{k}_{0}+ \overline{c}_{8}, $$

$$C = (b_{1} + b_{2} y)x + \frac{y^{7}}{1008} \frac{g}{\nu_{2}} ({\beta}_{2} {a^{2}_{2}}+{\gamma} b_{2}) \left\{ \frac{b_{2}}{ D } - {\alpha} B_{2} \right\} + $$

$$+ \frac{y^{6}}{720} \frac{g}{\nu_{2}} \left\{ \left[\frac{b_{1}}{ D } - {\alpha} B_{1} \right]({\beta}_{2} {a^{2}_{2}}+{\gamma} b_{2}) + 4 \left[ \frac{ b_{2}}{ D } - {\alpha} B_{2} \right] \times\right. $$

$$\left.\times\,({\beta}_{2} A+{\gamma} b_{1}) \right\} + \frac{y^{5}}{120} \left\{ \frac{g }{\nu_{2}} ({\beta}_{2} A+{\gamma} b_{1}) \left[\frac{b_{1}}{D} -{\alpha} B_{1} \right] +\right. $$

$$\left.+ 3 \left[\frac{ b_{2}}{ D } - {\alpha} B_{2} \right] \overline{c}_{1} \right\} +\frac{y^{4}}{24} \left\{ \left[\frac{ b_{1}}{ D } -{\alpha} B_{1} \right] \overline{c}_{1} + 2 \left[ \frac{ b_{2}}{ D } -{\alpha} B_{2} \right] \overline{c}_{2} \right\} + $$

$$+ \frac{y^{3}}{6} \left\{ \left[\frac{ b_{1}}{ D } - {\alpha} B_{1} \right] \overline{c}_{2} + \left[\frac{ b_{2}}{ D } -{\alpha} B_{2} \right] \overline{c}_{3} \right\} + $$

$$+\frac{y^{2}}{2} \left\{ \frac{ b_{1}}{ D } - {\alpha} B_{1} \right\} \overline{c}_{3} + y \overline{c}_{6} + \overline{c}_{7}. $$

Here

$$\overline{k}_{7}=\frac{1}{1008} \frac{\rho_{2} g^{2}}{\nu_{2}} ({\beta}_{2}{a^{2}_{2}}+ {\gamma} b_{2}) \left[ ({\beta}_{2} - {\alpha} {\gamma}) B_{2} + \frac {{\gamma} b_{2}}{D} \right], $$

$$\overline{k}_{6}=\frac{1}{720} \frac{\rho_{2} g^{2}}{\nu_{2}} \left\{ ({\beta}_{2} {a_{2}^{2}}+ {\gamma} b_{2}) \left[B_{1} ({\beta}_{2} -{\alpha} {\gamma}) + \frac{{\gamma} b_{1}}{D} \right] +\right. $$

$$\left.+ 4({\beta}_{2} A+ {\gamma} b_{1}) \left[B_{2} ({\beta}_{2} -{\alpha} {\gamma}) + \frac{{\gamma} b_{2}}{D} \right]\right\}, $$

$$\overline{k}_{5}=\frac{\rho_{2}g}{120}\left\{ \frac{g}{\nu_{2}} ({\beta}_{2} A +{\gamma} b_{1}) \left[B_{1} ({\beta}_{2} -{\alpha} {\gamma})+ \frac{{\gamma} b_{1}}{D} \right] +\right. $$

$$\left.+ 3 \left[ B_{2} ({\beta}_{2} -{\alpha} {\gamma}) + \frac{{\gamma} b_{2}}{D}\right] \overline{c}_{1} \right\}, $$

$$\overline{k}_{4}=\frac{\rho_{2}g}{24}\left\{ \left[B_{1} ({\beta}_{2} -{\alpha} {\gamma})+ \frac{{\gamma} b_{1}}{D}\right] \overline{c}_{1} +\right. $$

$$\left.+ 2 \left[ B_{2} ({\beta}_{2} -{\alpha} {\gamma}) + \frac{{\gamma} b_{2}}{D}\right] \overline{c}_{2} \right\}, $$

$$\overline{k}_{3} =\frac{\rho_{2}g}{6}\left\{ \left[B_{1} ({\beta}_{2} -{\alpha} {\gamma})+ \frac{{\gamma} b_{1}}{D}\right] \overline{c}_{2} +\right. $$

$$\left.+ \left[ B_{2} ({\beta}_{2} -{\alpha} {\gamma}) + \frac{{\gamma} b_{2}}{D}\right] \overline{c}_{3} \right\}, $$

$$\overline{k}_{2}=\frac{\rho_{2}g}{2}\left[ B_{1}({\beta}_{2} -{\alpha} {\gamma})+ \frac{{\gamma} b_{1}}{D} \right] \overline{c}_{3}, $$

$$\overline{k}_{1}=\rho_{2} g {\beta}_{2} \overline{c}_{4} + \rho_{2} g {\gamma}_{2} \overline{c}_{6}, \;\; \overline{k}_{0}=\rho_{2} g {\beta}_{2} \overline{c}_{5} + \rho_{2} g {\gamma} \overline{c}_{7}. $$

$$B_{1} =\displaystyle \frac{D A - \chi_{2} \delta b_{1}}{D \chi_{2} (1 - {\alpha} \delta)}, \quad \ B_{2} = \displaystyle \frac{D {a_{2}^{2}} - \chi_{2} \delta b_{2}}{D \chi_{2} (1 - {\alpha} \delta)}. $$

Determination of Integration Constants

$$b_{2}x + \phi^{\prime}(y) + {\alpha} {a_{2}^{2}}x + {\alpha} \vartheta_{2}^{\prime}(y)= 0 $$

and

$$ \left\{ \begin{array}{ll} b_{2}+{\alpha} {a_{2}^{2}} = 0 & \Rightarrow b_{2} = -\,{\alpha} {a^{2}_{2}},\\ \phi^{\prime}(h_{2})+{\alpha}\vartheta_{2}^{\prime}(h_{2}) = 0. & \end{array} \right. $$

(A.1)

The conditions of velocity and temperature continuity (2.9) result in the relations

$$c_{3}=\overline{c}_{3}, \qquad c_{5}= \overline{c}_{5}. $$

Due to the linear temperature distribution on the rigid walls (2.7) we have

$$\vartheta_{1} (-h_{1}) = \vartheta^{-}, \quad \vartheta_{2} (h_{2}) = \vartheta^{+} $$

$$ {a_{2}^{1}} = \frac{A- A_{1}}{h_{1}}, \quad {a_{2}^{2}} = \frac{A_{2} - A}{h_{2}}, $$

(A.2)

The mass balance condition leads to the following relations

$$ M= -D \rho_{2} (\overline{c}_{6} + {\alpha} \overline{c}_{4}), \qquad b_{2} + {\alpha} {a_{2}^{2}} = 0. $$

(A.3)

The following equations are the consequence of the heat transfer condition (2.12) at the interface $y = 0$:

$$ \begin{array}{cccc} {\kappa}_{1} {a^{1}_{2}} - {\kappa}_{2} {a_{2}^{2}} - \delta {\kappa}_{2} b_{2}= 0, \\ {\kappa}_{1} c_{4} - {\kappa}_{2} \overline{c}_{4} -\delta {\kappa}_{2} \overline{c}_{6} = -\lambda M, \end{array} $$

(A.4)

The first equality defines the following relation between ${a^{1}_{2}}$ and ${a_{2}^{2}}$:

$${a_{2}^{2}}= K_{a} {a_{2}^{1}}, \quad K_{a} = \frac{{\kappa}_{1}}{{\kappa}_{2}(1-{\alpha}\delta)}. $$

Herein condition (A.1) is taken into account. Since ${a^{1}_{2}}$ and ${a_{2}^{2}}$ are expressed in terms of A, $A_{1}$ and $A_{2}$ (see (A.2)), then, the following correlation is valid:

$$ A = \frac{A_{2} + \frac{h_{2}}{h_{1}}K_{a} A_{1}}{1+\frac{h_{2}}{h_{1}}K_{a}}. $$

(A.5)

The case of the equal longitudinal temperature gradients can be realized $A=A_{1}=A_{2}$, so that ${a_{2}^{1}}={a_{2}^{2}}$.

The consequence of the Clayperon–Clausius equation in the linearized form (2.13) leads to the equalities

$$b_{1} = C_{*} \varepsilon A, \qquad \overline{c}_{7} =C_{*} + C_{*} \varepsilon (\overline{c}_{5}-T_{0}). $$

From dynamic conditions (2.11) it follows that

$$c_{2} = \frac{\rho_{2} \nu_{2}}{\rho_{1} \nu_{1}} \overline{c}_{2} + \frac{\sigma_{T} A}{\rho_{1} \nu_{1}}, \qquad c_{1} = \frac{\rho_{2} \nu_{2}}{\rho_{1} \nu_{1}} \overline{c}_{1}. $$

The system of equations to determine the unknown integration constants $\overline {c}_{1}$, $\overline {c}_{2}$, $\overline {c}_{3}$ results from no-slip conditions (2.6) and conditions of the given gas flow rate (2.14):

$$\frac{l^{2}}{2} \frac{\rho_{2} \nu_{2}}{\rho_{1} \nu_{1}} \overline{c}_{1} - l \frac{\rho_{2} \nu_{2}}{\rho_{1} \nu_{1}} \overline{c}_{2} +\overline{c}_{3} = l \frac{\sigma_{T} A }{\rho_{1} \nu_{1}} - \frac{g {\beta}_{1}}{\nu_{1}}\left( \frac{l^{4}}{24}{a_{2}^{1}}- \frac{l^{3}}{6}A\right), $$

$$\frac{h^{2}}{2} \overline{c}_{1}+h \overline{c}_{2} + \overline{c}_{3} =$$

$$- \frac{g}{\nu_{2}} \left( \frac{h^{4}}{24}({\beta}_{2}{a_{2}^{2}}+{\gamma} b_{2})+\frac{h^{3}}{6}({\beta}_{2} A+{\gamma}b_{1})\right), $$

$$\frac{h^{3}}{6} \overline{c}_{1} + \frac{h^{2}}{2} \overline{c}_{2} + h \overline{c}_{3} = $$

$$\frac{Q}{\rho_{2}} - \frac{g}{\nu_{2}} \left( \frac{h^{5}}{120} ({\beta}_{2} {a_{2}^{2}} +{\gamma} b_{2})+\frac{h^{4}}{24} ({\beta}_{2} A + {\gamma} b_{1})\right). $$

If $\overline {c}_{1}$, $\overline {c}_{2}$, $\overline {c}_{3}$ have been calculated, then $c_{1}$, $c_{2}$, $c_{3}$ can be found.

In view of the exact solution form and the second equality in (A.1), we have the relationship between the constants $\overline {c}_{4}$ and $\overline {c}_{6}$:

$${\alpha}\overline{c}_{4}+\overline{c}_{6} = F, $$

$$F =-\frac{h^{6}}{144}\frac{g}{\nu_{2}}\frac{b_{2}}{D}{a_{2}^{2}}({\beta}_{2}-{\alpha}{\gamma})- $$

$$-\frac{h^{5}}{120}\frac{g}{\nu_{2}}\left( \frac{b_{1}}{D}{a_{2}^{2}}({\beta}_{2}-{\alpha}{\gamma}) + 4\frac{b_{2}}{D}({\beta}_{2} A + {\gamma} b_{1})\right) -$$

$$-\frac{h^{4}}{24}\left( \frac{g}{\nu_{2}}\frac{b_{1}}{D} ({\beta}_{2} A + {\gamma} b_{1}) + 3\frac{b_{2}}{D}\overline{c}_{1}\right) - $$

$$-\frac{h^{3}}{6} \left( \frac{b_{1}}{D}\overline{c}_{1} + 2\frac{b_{2}}{D} \overline{c}_{2} \right)- $$

$$- \frac{h^{2}}{2} \left( \frac{b_{1}}{D}\overline{c}_{2} +\frac{b_{2}}{D} \overline{c}_{3} \right) - h \frac{b_{1}}{D}\overline{c}_{3}. $$

The mass of the evaporating liquid is calculated with the help of the first from the sequences of the mass balance Eq. A.3: $M = -D\rho _{2} F$.

The second equality from (A.4) sets the dependence of the integration constant $c_{4}$ on $\overline {c}_{4}$ and $\overline {c}_{6}$:

$$c_{4} = \frac{{\kappa}_{2}}{{\kappa}_{1}}\overline{c}_{4} +\frac{\delta{\kappa}_{2}}{{\kappa}_{1}} \overline{c}_{6} -\frac{\lambda M}{{\kappa}_{1}}. $$

The constants $\overline {c}_{4}$, $\overline {c}_{6}$ and $c_{5}$ are determined from the system of equations being the result of the conditions for the temperature on the solid channel walls $\vartheta _{1} (-h_{1}) = \vartheta ^{-}$, $\vartheta _{2} (h_{2}) = \vartheta ^{+}$ (see (A.2)) and mass balance Eq. A.3:

$$- l \frac{{\kappa}_{2}}{{\kappa}_{1}}\overline{c}_{4} - l \frac{\delta{\kappa}_{2}}{{\kappa}_{1}} \overline{c}_{6} + c_{5} = \vartheta^{-} + \frac{l^{7}}{1008}\frac{g{\beta}_{1}({a_{2}^{1}})^{2}}{\nu_{1}\chi_{1}}- $$

$$-\frac{l^{6}}{144}\frac{g{\beta}_{1} A {a_{2}^{1}}}{\nu_{1}\chi_{1}}+ \frac{l^{5}}{120} \left( \frac{g {\beta}_{1} A^{2}}{\chi_{1} \nu_{1}}+\frac{3{a_{2}^{1}}}{\chi_{1}}c_{1}\right) - $$

$$\frac{l^{4}}{24}\left( \frac{A}{\chi_{1}} c_{1} +\frac{2{a_{2}^{1}}}{\chi_{1}}c_{2} \right) +\frac{l^{3}}{6}\left( \frac{A}{\chi_{1}} c_{2} + \frac{{a_{2}^{1}}}{\chi_{1}}c_{3}\right) - $$

$$- \frac{l^{2}}{2} \frac{A}{\chi_{1}} c_{3} -l\frac{\lambda M}{{\kappa}_{1}}, $$

$$h \overline{c}_{4} + c_{5} = \vartheta^{+} - \frac{h_{7}}{1008}B_{2}\frac{g}{\nu_{2}}\left( {\beta}_{2} {a_{2}^{2}} + {\gamma} b_{2}\right) - $$

$$- \frac{h^{6}}{720}\frac{g}{\nu_{2}}\left[B_{1}\left( {\beta}_{2} {a_{2}^{2}} + {\gamma} b_{2}\right) + + 4B_{2}\left( {\beta}_{2} A + {\gamma} b_{1}\right)\right]- $$

$$- \frac{h^{5}}{120} \left[B_{1} \frac{g}{\nu_{2}} ({\beta}_{2} A + {\gamma} b_{1}) + 3B_{2} \overline{c}_{1}\right] - \frac{h^{4}}{24}\left[B_{1} \overline{c}_{1} + 2B_{2}\overline{c}_{2} \right] - $$

$$- \frac{h^{3}}{6} \left[B_{1} \overline{c}_{2} + B_{2}\overline{c}_{3} \right] - \frac{h^{2}}{2} B_{1} \overline{c}_{3}, $$

$${\alpha}\overline{c}_{4}+\overline{c}_{6} = F. $$

Here, the condition $c_{5}= \overline {c}_{5}$ and the second relationship from (A.3) are taken into account.

A special case $b_{2} = 0$ (${a_{2}^{2}} = {a_{2}^{1}} = 0$s) can be realized.