Abstract
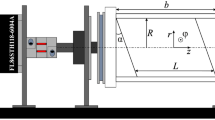
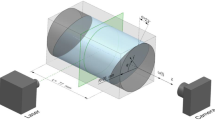
The fluid flow in a non-uniformly rotating (librating) cylinder about a horizontal axis is experimentally studied. In the absence of librations the fluid performs a solid-body rotation together with the cavity. Librations lead to the appearance of steady zonal flow in the whole cylinder and the intensive steady toroidal flows near the cavity corners. If the frequency of librations is twice lower than the mean rotation rate the inertial waves are excited. The oscillating motion associated with the propagation of inertial wave in the fluid bulk leads to the appearance of an additional steady flow in the Stokes boundary layers on the cavity side wall. In this case the heavy particles of the visualizer are assembled on the side wall into ring structures. The patterns are determined by the structure of steady flow, which in turn depends on the number of reflections of inertial wave beams from the cavity side wall. For some frequencies, inertial waves experience spatial resonance, resulting in inertial modes, which are eigenmodes of the cavity geometry. The resonance of the inertial modes modifies the steady flow structure close to the boundary layer that is manifested in the direct rebuilding of patterns. It is shown that the intensity of zonal flow, as well as the intensity of steady flows excited by inertial waves, is proportional to the square of the amplitude of librations.










Similar content being viewed by others
References
Boisson, J., Lamriben, C., Maas, L.R.M., Cortet, P., Moisy, F.: Inertial waves and modes excited by the libration of a rotating cube. Phys. Fluids 24, 076602 (2012)
Borcia, I.D., Abouzar, G.V., Harlander, U.: Inertial wave mode excitation in a rotating annulus with partially librating boundaries. Fluid Dyn. Res. 46, 041423 (2014)
Brouzet, C., Sibgatullin, I.N., Scolan, H., Ermanyuk, E.V., Dauxois, T.: Internal wave attractors examined using laboratory experiments and 3D numerical simulations. J. Fluid Mech. 793, 109–131 (2016)
Brungs, S., Egli, M., Wuest, S.L., Christianen, P.C.M., Van Loon, J.J.W.A., Ngo Anh, T.J., Hemmersbach, R.: Facilities for simulation of microgravity in the ESA ground-based facility programme. Microgravity Sci. Technol. 28, 191–203 (2016)
Busse, F.H.: Mean zonal flows generated by librations of a rotating spherical cavity. J. Fluid Mech. 650, 505–512 (2010)
Busse, F.H.: Zonal flow induced by longitudinal librations of a rotating cylindrical cavity. Physica D 240, 208–211 (2011)
Calkins, M.A., Noir, J., Eldredge, J.D., Aurnou, J.M.: Axisymmetric simulations of libration-driven fluid dynamics in a spherical shell geometry. Phys. Fluids 22, 086602 (2010)
Ermanyuk, E.V., Gavrilov, N.V.: Internal-wave radiation and optical measurements in stratified fluids. Microgravity Sci. Technol. 19, 144–147 (2007)
Favier, B., Barker, A., Baruteau, C., Ogilvie, G.: Nonlinear evolution of tidally forced inertial waves in rotating fluid bodies. Mon. Not. R. Astron. Soc. 439, 845–860 (2014)
Greenspan, H.P.: The Theory of Rotating Fluids. University Press, Cambridge (1968)
Hoff, M., Harlander, U., Egbers, C.: Experimental survey of linear and nonlinear inertial waves and wave instabilities in a spherical shell. J. Fluid Mech. 789, 589–616 (2016)
Kerswell, R.: On the internal shear layers spawned by the critical regions in oscillatory Ekman boundary layers. J. Fluid Mech. 298, 311–325 (1995)
Klein, M., Seelig, T., Kurgansky, M.V., Ghasemi, A.V., Borcia, I.D., Will, A., Schaller, E., Egbers, C., Harlander, U.: Inertial wave excitation and focusing in a liquid bounded by a frustum and a cylinder. J. Fluid Mech. 751, 255–297 (2014)
Koch, S., Harlander, U., Egbers, C., Hollerbach, R.: Inertial waves in a spherical shell induced by librations of the inner sphere: Expe- rimental and numerical results. Fluid Dyn. Res. 45, 035504 (2013)
Kozlov, V.G., Kozlov, N.V.: Vibrational dynamics of a light body in a liquid-filled rotating cylinder. Fluid Dyn. 43(1), 9–19 (2008)
Kozlov, V.G., Ivanova, A.A.: Dramatic effect of vibrations on dynamics of rotating hydrodynamic systems. Microgravity Sci. Technol. 21, 339–348 (2009)
Kozlov, V., Polezhaev, D.: Flow patterns in a rotating horizontal cylinder partially filled with liquid. Phys. Rev. E 92, 013016 (2015)
Kozlov, V.G., Ivanova, A.A., Vjatkin, A.A., Sabirov, R.R.: Vibrational convection of heat-generating fluid in a rotating horizontal cylinder. The role of relative cavity length. Acta Astronaut. 112, 48–55 (2015)
Kozlov, V.G., Kozlov, N.V., Subbotin, S.V.: Steady flows excited by circular oscillations of free inner core in rotating spherical cavity. Eur. J. Mech. B-Fluids 58(4), 85–94 (2016)
Le Bars, M., Cébron, D., Le Gal, P.: Flows driven by libration, precession, and tides. Annu. Rev. Fluid Mech. 47, 163–193 (2015)
Lopez, J.M., Marques, F.: Rapidly rotating cylinder flow with an oscillating sidewall. Phys. Rev. E. 89, 013013 (2014)
Margot, J.L., Peale, S.J., Jurgens, R.F., Slade, M.A., Holin, I.V.: Large longitude libration of Mercury reveals a molten core. Science 316, 710–714 (2007)
McEwan, A.D.: Inertial oscillations in a rotating fluid cylinder. J. Fluid Mech. 40, 603–639 (1970)
Messio, L., Morize, C., Rabaud, M., Moisy, F.: Experimental observation using particle image velocimetry of inertial waves in a rotating fluid. Exp. Fluids 44, 519–528 (2008)
Morize, C., Le Bars, M., Le Gal, P., Tilgner, A.: Experimental determination of zonal winds driven by tides. Phys. Rev. Lett. 104, 214501 (2010)
Noir, J., Calkins, M.A., Lasbleis, M., Cantwell, J., Aurnou, J.M.: Experimental study of libration-driven zonal flows in a straight cylinder. Phys. Earth Planet Inter. 182, 98–106 (2010)
Rieutord, M., Georgeot, B., Valdettaro, L.: Inertial waves in a rotating spherical shell: attractors and asymptotic spectrum. J. Fluid Mech. 435, 103–144 (2001)
Sauret, A., Le Dizès, S.: Steady flow induced by longitudinal libration in a spherical shell. J. Fluid Mech. 718, 181–209 (2013)
Sauret, A., Cebron, D., Morize, C., Le Bars, M.: Experimental and numerical study of mean zonal flows generated by librations of a rotating spherical cavity. J. Fluid Mech. 662, 260–268 (2010)
Sauret, A., Cébron, D., Le Bars, M., Le Dizès, S.: Fluid flows in a librating cylinder. Phys. Fluids 24, 026603 (2012)
Sauret, A., Le Bars, M., Le Gal, P.: Tide-driven shear instability in planetary liquid cores. Geophys. Res. Lett. 41, 6078–6083 (2014)
Tilgner, A.: Zonal wind driven by inertial modes. Phys. Rev. Lett. 99, 194501 (2007)
Thielicke, W., Stamhuis, E.J.: PIVLab – Time-resolved digital particle image velocimetry tool for MATLAB (version: 1.41). J. Open Res. Software 2(1), e30 (2014)
Wang, C.Y.: Cylindrical tank of fluid oscillating about a steady rotation. J. Fluid Mech. 41, 581–592 (1970)
Warnke, E., Kopp, S., Wehland, M., Hemmersbach, R., Bauer, J., Pietsch, J., Infanger, M., Grimm D.: Thyroid cells exposed to simulated microgravity conditions – comparison of the fast rotating clinostat and the random positioning machine. Microgravity Sci. Technol. 28, 247–260 (2016)
Acknowledgments
The research was supported by the Russian Foundation for Basic Research (project Nos. 16-31-60099 mol_a_dk and16-31-00169 mol_a) and grant of the President of the Russian Federation for the support of Leading Scientific Schools of the Russian Federation (grant NSh-9176.2016.1). We are grateful to Professor V.G. Kozlov for a fruitful discussion of the experimental results.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article belongs to the Topical Collection: Non-Equilibrium Processes in Continuous Media under Microgravity
Guest Editor: Tatyana Lyubimova
Rights and permissions
About this article
Cite this article
Subbotin, S., Dyakova, V. Inertial Waves and Steady Flows in a Liquid Filled Librating Cylinder. Microgravity Sci. Technol. 30, 383–392 (2018). https://doi.org/10.1007/s12217-018-9621-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12217-018-9621-x