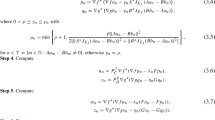Skip to main content
SpringerLink
Log in

Equilibrium problems under relaxed α-monotonicity on Hadamard manifolds

  • Published:
Rendiconti del Circolo Matematico di Palermo Series 2 Aims and scope Submit manuscript

Abstract

In this paper, we study the existence of solutions of both equilibrium problems and mixed equilibrium problems on Hadamard manifolds. Under relaxed \(\alpha \)-pseudomonotonicity assumption on the underlying bifunction we prove that the solution set of the equilibrium problem is nonempty. We also provide the existence of solution of mixed equilibrium problems with relaxed \(\alpha \)-monotonicity. The results presented in this paper generalize and improve some known results given in literature, see for example (Colao et al. in J Math Anal Appl 388:61–77, 2012; Jana and Nahak in Rend Circ Mat Palermo(2) 65(1):97–109, 2016; Mahato and Nahak in OPSEARCH, 2013. https://doi.org/10.1007/s12597-013-0142-5).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bianchi, M., Schaible, S.: Generalized monotone bifunctions and equilibrium problems. J. Optim. Theory Appl. 90, 31–43 (1996)

    Article  MathSciNet  Google Scholar 

  2. Blum, E., Oettli, W.: From optimization and variational inequalities to equilibrium problems. Math. Student 63, 123–145 (1994)

    MathSciNet  MATH  Google Scholar 

  3. Colao, V., López, G., Marino, G., Martín-Márquez, V.: Equilibrium problems in Hadamard manifolds. J. Math. Anal. Appl. 388, 61–77 (2012)

    Article  MathSciNet  Google Scholar 

  4. Cruz Neto, J.X., Ferreira, O.P., Lucambio Pérez, L.R., Németh, S.Z.: Convex- and Monotone-Transformable Mathematical Programming Problems and a Proximal-Like Point Method. J. Global Optim. 35, 53–69 (2006)

    Article  MathSciNet  Google Scholar 

  5. Ferreira, O.P., Oliveira, P.R.: Proximal point algorithm on Riemannian manifolds. Optimization 51, 257–270 (2002)

    Article  MathSciNet  Google Scholar 

  6. Jana, S., Nahak, C.: Mixed equilibrium problems on Hadamard manifolds. Rend. Circ. Mat. Palermo(2) 65(1), 97–109 (2016)

    Article  MathSciNet  Google Scholar 

  7. Jost, J.: Nonpositive Curvature: Geometric and Analytic Aspects. Birkhauser Verlag, Basel (1997)

    Book  Google Scholar 

  8. Li, C., López, G., Martín-Márquez, V.: Monotone vector fields and the proximal point algorithm on Hadamard manifolds. J. Lond. Math. Soc. 79, 663–683 (2009)

    Article  MathSciNet  Google Scholar 

  9. Li, S.L., Li, C., Liou, Y.C., Yao, J.C.: Existence of solutions for variational inequalities on Riemannian manifolds. Nonlinear Anal. 71, 5695–5706 (2009)

    Article  MathSciNet  Google Scholar 

  10. Li, X.B., Huang, N.J.: Generalized vector quasi-equilibrium problems on Hadamard manifolds. Optim. Lett. https://doi.org/10.1007/s11590-013-0703-9

  11. Luc, D.T.: Existence results for densely pseudomonotone variational inequalities. J. Math. Anal. Appl. 254, 309–320 (2001)

    Article  MathSciNet  Google Scholar 

  12. Németh, S.Z.: Variational inequalities on Hadamard manifolds. Nonlinear Anal. 52, 1491–1498 (2003)

    Article  MathSciNet  Google Scholar 

  13. Németh, S.Z.: Geodesic monotone vector fields. Lobachevskii J. Math. 5, 13–28 (1999)

    MathSciNet  MATH  Google Scholar 

  14. Mahato, N.K., Nahak, C.: Equilibrium problems with generalized relaxed monotonicities in Banach spaces. OPSEARCH. https://doi.org/10.1007/s12597-013-0142-5

  15. Rapcsák, T.: Geodesic convexity in nonlinear optimization. J. Optim. Theory Appl. 69, 169–183 (1991)

    Article  MathSciNet  Google Scholar 

  16. Reich, S., Sabach, S.: Three strong convergence theorems regarding iterative methods for solving equilibrium problems in reflexive Banach spaces. Contempor. Math. 68, 225–240 (2012)

    Article  MathSciNet  Google Scholar 

  17. Sakai, T.: Riemannian Geometry, Translations of Mathematical Monographs, vol. 149. American Mathematical Society, Providence (1996)

    Book  Google Scholar 

  18. Tang, G.J., Zhou, L.W., Huang, N.J.: The proximal point algorithm for pseudomonotone variational inequalities on Hadamard manifolds. Optim. Lett. (2012). https://doi.org/10.1007/s11590-012-0459-7

  19. Udriste, C.: Convex Functions and Optimization Methods on Riemannian Manifolds, vol. 297. Kluwer Academic (1994)

  20. Wang, J.H., López, G., Martín-Márquez, V., Li, C.: Monotone and accretive vector fields on Riemannian manifolds. J. Optim. Theory Appl. 146, 691–708 (2010)

    Article  MathSciNet  Google Scholar 

  21. Yao, Y., Noor, M.A., Zainab, S., Liou, Y.C.: Mixed equilibrium problems and optimization problems. J. Math. Anal. Appl. 354, 319–329 (2009)

    Article  MathSciNet  Google Scholar 

  22. Zhou, L.W., Huang, N.J.: Generalized KKM theorems on Hadamard manifolds with applications. http://www.paper.edu.cn/index.php/default/releasepaper/content/200906-669 (2009)

Download references

Acknowledgements

The author wishes to thank the referees for their valuable comments and suggestions to improve the presentation of this paper.

Author information

Authors and Affiliations

  1. Department of Mathematics, Narajole Raj College, West Midnapore, West Bengal, 721211, India

    S. Jana

Authors
  1. S. Jana
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Jana.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jana, S. Equilibrium problems under relaxed α-monotonicity on Hadamard manifolds. Rend. Circ. Mat. Palermo, II. Ser 71, 361–372 (2022). https://doi.org/10.1007/s12215-021-00595-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12215-021-00595-w

Keywords

Mathematics Subject Classification

Search

Navigation