Skip to main content
SpringerLink
Log in

Adaptive finite element analysis of steel girder deck pavement

  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

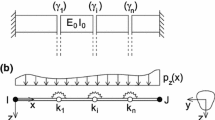
This paper shows a more exact and practical finite element model of the steel girder deck pavement. Based on Mindlin thick plate theory, a 12-node solid thick plate element was constituted to analyze the pavement. The computation result was compared with that by traditional 4-node and 8-node thick plate finite element, and is satisfactory. A combined plate beam element method is presented to investigate the stiffened plate. A 6-node solid thin plate element was constituted to analyze the top plate based on Kirchhoff thin plate theory. The stiffeners acting as the vertical supporting function mainly are taken as Euler beam elements. A method of using the linear interpolation to realize the longitudinal displacement and the cubic Hermite interpolation to the vertical displacement is presented to analyze the stiffeners. In addition, it is essential to consider the displacement coordination between the top plate and stiffeners. A node-to-node contact scheme, which is applicable for three-dimensional contact analyses involving large deformations, was used to treat the contact problem between pavement and stiffened plate by Lagrange multiplier methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. C. T. Metcalf, Flexural tests of paving materials for orthotropic steel plate bridges, Highway Research Record, 155 (1967) 56–78.

    Google Scholar 

  2. M. S. G. Cullimore, I. D. Flett and J. W. Smith, Flexure of steel bridge deck plate with asphalt surfacing, IABSE Periodical, Bristol: University of Bristol, 1 (1983) 58–83.

    Google Scholar 

  3. Koroneose, Oscillations measurements of an orthotropic roadway deck with bituminous cover, Bitumen Teere Asphalt Peche, 5 (1971) 223–236.

    Google Scholar 

  4. M. H. Kolstein and J. H. Dijkink, Behavior of modified bituminous surfacing on orthotropic steel bridge decks, Proceedings of the 4th Euro-bitumen Symposium, 1 (1989) 907–975.

    Google Scholar 

  5. M. H. Kolstein and J. Wardenier, Stress reduction due to surfacing on orthotropic steel decks, Proceedings of the ISAB Workshop: Evaluation of Existing Steel and Composite Bridges (1997).

    Google Scholar 

  6. G. H. Gunther, S. Bild and G. Sedlacek, Durability of asphaltic pavements on orthotropic decks of steel bridges, Construct Steel Research, 7 (1987) 5–106.

    Google Scholar 

  7. S. Bild, Durability design criteria for bituminous pavements on orthotropic steel bridge decks, Can. J. Civ. Eng., 14 (1) (1987) 41–48.

    Article  Google Scholar 

  8. H. Nakanishi and T. Okochi, The structural evaluation for an asphalt pavement, AAPA (2000) 113–123.

    Google Scholar 

  9. T. Nishizawa, K. Himeno, K. Nomura and K. Uchida, Development of a new structural model with prism and strip elements for pavement on steel bridge decks, The International J. of Geomechanics, 1 (3) (2001) 351–369.

    Article  Google Scholar 

  10. R. Szilard, Theories and applications of plate analysis, Hoboken, New Jersey, USA: John Wiley&Sons (2004).

    Book  Google Scholar 

  11. E. Reissner, The effect of transverse shear deformation on the bending of elastic plate, Transactions of ASME J. Applied Mechanics, 12 (1945) A69–A77.

    MathSciNet  MATH  Google Scholar 

  12. R. D. Mindlin, Influence of rotary inertia and shear on flexural motions of isotropic elastic plates, J. of Applied Mechanics, 18 (1) (1951) 31–38.

    MATH  Google Scholar 

  13. C. Y. Chia, Non-linear analysis of plates, McGraw-Hill, New York (1980).

    Google Scholar 

  14. I. Senjanovc, N. Vladimir and D. S. Cho, A new finite element formulation for vibration analysis of thick plates, Int. J. Nav. Archit. Ocean Eng., 7 (2015) 324–345.

    Article  Google Scholar 

  15. T. J. R. Hughes, R. L. Taylor and W. Kanoknukulchai, Simple and efficient element for plate bending, International J. for Numerical Methods in Engineering, 11 (10) (1977) 1529–1543.

    Article  MATH  Google Scholar 

  16. C. Lovadina, Analysis of a mixed finite element method for the Reissner-Mindlin plate problems, Computer Methods in Applied Mechanics and Engineering, 163 (1998) 71–85.

    Article  MathSciNet  MATH  Google Scholar 

  17. O. C. Zienkiewicz and R. L. Taylor, The finite element method, 5th ed., Oxford: Butterworth-Heinemann (2000).

    MATH  Google Scholar 

  18. K. Bletzinger, M. Bischoff and E. Ramm, A unified approach for shear-locking-free triangular and rectangular shell finite elements, Computers and Structures, 75 (3) (2000) 321–334.

    Article  Google Scholar 

  19. H. Nguyen-Xuan, G. R. Liu, C. Thai-Hoang and T. Nguyen-Thoi, An Edge-based smoothed Finite element method (ES-FEM) with stabilized discrete shear gap technique for analysis of Reissner-Mindlin plates, Computer Methods in Applied Mechanics and Engineering, 199 (9–12) (2010) 471–489.

    Article  MathSciNet  MATH  Google Scholar 

  20. P. Wriggers, Computational contact mechanics, Springer, New York (2007).

    Book  MATH  Google Scholar 

  21. P. Wriggers and J. C. Simo, A note on tangent stiffness for fully nonlinear contact problems, Comp. Appl. Num. Meth., 1 (1985) 199–203.

    Article  MATH  Google Scholar 

  22. J. T. Oden, Exterior penalty methods for contact problems in elasticity, Wunderlich KJBW, E. Stein (ed), Nonlinear Finite Element Analysis in Structural Mechanics, Springer, Berlin (1981).

  23. S. Jin, D. Sohn and S. Im, Node-to-node scheme for threedimensional contact mechanics using polyhedral type variable-node elements, Comput. Methods Appl. Mech. Engrg., 304 (2016) 217–242.

    Article  MathSciNet  Google Scholar 

  24. G. Pietrzak, Continuum mechanics modelling and augmented lagrange formulation of large deformation frictional contact problems, Technical Report 1656, Ecole polytechnique federale de Lausanne, EPFL (1997).

    Google Scholar 

  25. A. R. Mijar and J. S. Arora, An augmented Lagrangian optimization method for contact analysis problems, 2: Numerical evaluation, Struct. Multidiscip. Optim., 28 (2004) 113–126.

    MathSciNet  MATH  Google Scholar 

  26. M. Chandrashekhar and R. Ganguli, Large deformation dynamic finite element analysis of delaminated composite plates using contact-impact conditions, Computers and Structures, 144 (2016) 92–102.

    Article  Google Scholar 

  27. A. P. C. Dias, A. L. Serpa and M. L. Bittencourt, Highorder mortar-based element applied to nonlinear analysis of structural contact mechanics, Comput. Methods Appl. Mech. Engrg., 294 (2015) 19–55.

    Article  MathSciNet  Google Scholar 

  28. C. J. Corbett and R. A. Sauer, Three-dimensional isogeometrically enriched finite elements for frictional contact and mixed-mode debonding, Comput. Methods Appl. Mech. Engrg., 284 (2015) 781–806.

    Article  MathSciNet  Google Scholar 

  29. Y.-W. Kim, Finite element formulation for earthquake analysis of single-span beams involving forced deformation caused by multi-support motions, J. of Mechanical Science and Technology, 29 (2) (2015) 461–469.

    Article  Google Scholar 

  30. Y.-J. Kee and S.-J. Shin, Structural dynamic modeling for rotating blades using three dimensional finite elements, J. of Mechanical Science and Technology, 29 (4) (2015) 1607–1618.

    Article  Google Scholar 

  31. J. Yang, Y. Lei, J. Han and S. Meng, Enriched finite element method for three-dimensional viscoelastic interface crack problems, J. of Mechanical Science and Technology, 30 (2) (2016) 771–782.

    Article  Google Scholar 

  32. W. A. Siswanto, M. Nagentrau, A. L. Mohd Tobi and M. N. Tamin, Prediction of plastic deformation under contact condition by quasi-static and dynamic simulations using explicit finite element analysis, J. of Mechanical Science and Technology, 30 (11) (2016) 5093–5101.

    Article  Google Scholar 

  33. D.-K. Shin, Verification of the performance of rotatable jig for a single cantilever beam method using the finite element analysis, J. of Mechanical Science and Technology, 31 (2) (2017) 777–784.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou, 510640, China

    Wenhuo Sun, Lixiong Gu & Ronghui Wang

  2. Research Institute of Highway Ministry of Transport, Beijing, 100088, China

    Tiedong Qi

Authors
  1. Wenhuo Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lixiong Gu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ronghui Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Tiedong Qi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wenhuo Sun.

Additional information

Recommended by Associate Editor Choon Yeol Lee

Wenhuo Sun is a doctoral candidate in Bridge and Tunnel Engineering at South China University of Technology, China. His current research area is mainly on the nonlinear dynamics analysis of the steel girder deck pavement using analytical method.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sun, W., Gu, L., Wang, R. et al. Adaptive finite element analysis of steel girder deck pavement. J Mech Sci Technol 32, 593–603 (2018). https://doi.org/10.1007/s12206-018-0106-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-018-0106-4

Keywords

Search

Navigation