Skip to main content
SpringerLink
Log in

Thermal Transport in Nanoporous Yttria-Stabilized Zirconia by Molecular Dynamics Simulation

  • Published:
Journal of Shanghai Jiaotong University (Science) Aims and scope Submit manuscript

Abstract

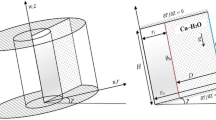
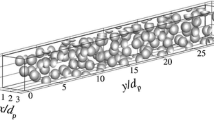
Yttria-stabilized zirconia (YSZ) is widely used as thermal barrier coatings (TBCs) to reduce heat transfer between hot gases and metallic components in gas-turbine engines. Porous structure can generally reduce the lattice thermal conductivity of bulk material, so porous YSZ can be potentially used as TBCs with better thermal performance. In this work, we investigate the thermal conductivity of nanoporous YSZ using the nonequilibrium molecular dynamics (NEMD) simulation, and comprehensively discuss the effects of cross-sectional area, pore size, structure length, porosity, Y2O3 concentration and temperature on the thermal conductivity. To compare with the results of the NEMD simulation, we solve the heat diffusion equation and the gray Boltzmann transport equation (BTE) to calculate the thermal conductivity of the same porous structure. From the results, we find that the thermal conductivity of YSZ has a weak dependence on the structure length at the length range from 10 to 26 nm, which indicates that the majority of heat carriers have very short mean free path (MFP) but there exists small percentage (about 3%) of phonons with longer MFP (larger than 10 nm) contributing to the thermal conductivity. The thermal conductivity predicted by NEMD simulation is smaller than that of solving heat diffusion equation (diffusive limit) with the same porous structure. It shows that the presence of pores affects phonon scattering and further affects the thermal conductivity of nanoporous YSZ. The results agree well with the solution of gray BTE with a average MFP of 0.6 nm. The thermal conductivity of nanoporous YSZ weakly depends on the Y2O3 concentration and temperature, which shows the phonons with very short MFP play the major contribution to the thermal conductivity. The results help to better understand the heat transfer in porous YSZ structure and develop better TBCs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. PADTURE N P, GELL M, JORDAN E H. Thermal barrier coatings for gas-turbine engine applications [J]. Science, 2002, 296(5566): 280–284.

    Article  Google Scholar 

  2. CAO X Q, VASSEN R, STOEVER D. Ceramic materials for thermal barrier coatings [J]. Journal of the European Ceramic Society, 2004, 24(1): 1–10.

    Article  Google Scholar 

  3. NATH S, MANNA I, MAJUMDAR J D. Nanomechanical behavior of yttria stabilized zirconia (YSZ) based thermal barrier coating [J]. Ceramics International, 2015, 41(4): 5247–5256.

    Article  Google Scholar 

  4. NAIT-ALI B, HABERKO K, VESTEGHEM H, et al. Thermal conductivity of highly porous zirconia [J]. Journal of the European Ceramic Society, 2006, 26(16): 3567–3574.

    Article  Google Scholar 

  5. PIA G, CASNEDI L, SANNA U. Porosity and pore size distribution influence on thermal conductivity of yttria-stabilized zirconia: Experimental findings and model predictions [J]. Ceramics International, 2016, 42(5): 5802–5809.

    Article  Google Scholar 

  6. SCHLICHTING K W, PADTURE N P, KLEMENS P G. Thermal conductivity of dense and porous yttriastabilized zirconia [J]. Journal of Materials Science, 2001, 36(12): 3003–3010.

    Article  Google Scholar 

  7. PIA G. High porous yttria-stabilized zirconia with aligned pore channels: Morphology directionality influence on heat transfer [J]. Ceramics International, 2016, 42(10): 11674–11681.

    Article  Google Scholar 

  8. NAN C W, BIRRINGER R, CLARKE D R, et al. Effective thermal conductivity of particulate composites with interfacial thermal resistance [J]. Journal of Applied Physics, 1997, 81(10): 6692–6699.

    Article  Google Scholar 

  9. BOURRET J, TESSIER-DOYEN N, NAIT-ALI B, et al. Effect of the pore volume fraction on the thermal conductivity and mechanical properties of kaolin-based foams [J]. Journal of the European Ceramic Society, 2013, 33(9): 1487–1495.

    Article  Google Scholar 

  10. CHUNG J D, KAVIANY M. Effects of phonon pore scattering and pore randomness on effective conductivity of porous silicon [J]. International Journal of Heat and Mass Transfer, 2000, 43(4): 521–538.

    Article  MATH  Google Scholar 

  11. HSIEH T Y, LIN H, HSIEH T J, et al. Thermal conductivity modeling of periodic porous silicon with aligned cylindrical pores [J]. Journal of Applied Physics, 2012, 111(12): 124329.

    Article  Google Scholar 

  12. WANG M, PAN N. Modeling and prediction of the effective thermal conductivity of random open-cell porous foams [J]. International Journal of Heat and Mass Transfer, 2008, 51(5/6): 1325–1331.

    Article  MATH  Google Scholar 

  13. WANG M, WANG J, PAN N, et al. Three-dimensional effect on the effective thermal conductivity of porous media [J]. Journal of Physics D: Applied Physics, 2006, 40(1): 260.

    Article  Google Scholar 

  14. GUO Y, WANG M. Lattice Boltzmann modeling of phonon transport [J]. Journal of Computational Physics, 2016, 315: 1–15.

    Article  MathSciNet  MATH  Google Scholar 

  15. LEE J H, GALLI G A, GROSSMAN J C. Nanoporous Si as an efficient thermoelectric material [J]. Nano Letters, 2008, 8(11): 3750–3754.

    Article  Google Scholar 

  16. HE Y, DONADIO D, LEE J H, et al. Thermal transport in nanoporous silicon: Interplay between disorder at mesoscopic and atomic scales [J]. ACS Nano, 2011, 5(3): 1839–1844.

    Article  Google Scholar 

  17. LAU K C, DUNLAP B I. Molecular dynamics simulation of yttria-stabilized zirconia (YSZ) crystalline and amorphous solids [J]. Journal of Physics: Condensed Matter, 2011, 23(3): 035401.

    Google Scholar 

  18. FREEMAN J J, ANDERSON A C. Thermal conductivity of amorphous solids [J]. Physical Review B, 1986, 34(8): 5684.

    Article  Google Scholar 

  19. HE Y, DONADIO D, GALLI G. Morphology and temperature dependence of the thermal conductivity of nanoporous SiGe [J]. Nano Letters, 2011, 11(9): 3608–3611.

    Article  Google Scholar 

  20. ZHOU XW, JONES R E. Effects of nano-void density, size and spatial population on thermal conductivity: A case study of GaN crystal [J]. Journal of Physics: Condensed Matter, 2012, 24(32): 325804.

    Google Scholar 

  21. BRINKMAN H W, BRIELS W J, VERWEIJ H. Molecular dynamics simulations of yttriastabilized zirconia [J]. Chemical Physics Letters, 1995, 247(4/5/6): 386–390.

    Article  Google Scholar 

  22. SCHELLING P K, PHILLPOT S R. Mechanism of thermal transport in zirconia and yttria-stabilized zirconia by molecular-dynamics simulation [J]. Journal of the American Ceramic Society, 2001, 84(12): 2997–3007.

    Article  Google Scholar 

  23. CARSON J K, LOVATT S J, TANNER D J, et al. An analysis of the influence of material structure on the effective thermal conductivity of theoretical porous materials using finite element simulations [J]. International Journal of Refrigeration, 2003, 26(8): 873–880.

    Article  Google Scholar 

  24. MURTHY J Y, MATHUR S R. Computation of submicron thermal transport using an unstructured finite volume method [J]. Journal of Heat Transfer, 2002, 124(6): 1176–1181.

    Article  Google Scholar 

  25. TIAN Z, HU H, SUN Y. A molecular dynamics study of effective thermal conductivity in nanocomposites [J]. International Journal of Heat and Mass Transfer, 2013, 61: 577–582.

    Article  Google Scholar 

  26. PLIMPTON S. Fast parallel algorithms for shortrange molecular dynamics [J]. Journal of Computational Physics, 1995, 117(1): 1–19.

    Article  MATH  Google Scholar 

  27. VAN BEEST B W H, KRAMER G J, VAN SANTEN R A. Force fields for silicas and aluminophosphates based on ab initio calculations [J]. Physical Review Letters, 1990, 64: 1955.

    Article  Google Scholar 

  28. ALDEBERT P, TRAVERSE J P. Structure and ionic mobility of zirconia at high temperature [J]. Journal of the American Ceramic Society, 1985, 68(1): 34–40.

    Article  Google Scholar 

  29. MINERVINI L, GRIMES R W, SICKAFUS K E. Disorder in pyrochlore oxides [J]. Journal of the American Ceramic Society, 2000, 83(8): 1873–1878.

    Article  Google Scholar 

  30. SCHELLING P K, PHILLPOT S R, KEBLINSKI P. Comparison of atomic-level simulation methods for computing thermal conductivity [J]. Physical Review B, 2002, 65(14): 144306.

    Article  Google Scholar 

  31. LUKES J R, TIEN C L. Molecular dynamics simulation of thermal conduction in nanoporous thin films [J]. Microscale Thermophysical Engineering, 2004, 8(4): 341–359.

    Article  Google Scholar 

  32. ZHANG X, BAO H, HU M. Bilateral substrate effect on the thermal conductivity of two-dimensional silicon [J]. Nanoscale, 2015, 7(14): 6014–6022.

    Article  Google Scholar 

Download references

Acknowledgement

Simulations were performed with computing resources granted by the High Performance Computing Center at Shanghai Jiao Tong University.

Author information

Authors and Affiliations

  1. University of Michigan - Shanghai Jiao Tong University Joint Institute, Shanghai Jiao Tong University, Shanghai, 200240, China

    Shuaishuai Zhao  (赵帅帅), Cheng Shao  (邵 成), Saeid Zahiri & Hua Bao  (鲍 华)

  2. School of Mechanical and Power Engineering, Shanghai Jiao Tong University, Shanghai, 200240, China

    Changying Zhao  (赵长颖)

Authors
  1. Shuaishuai Zhao  (赵帅帅)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Cheng Shao  (邵 成)
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Saeid Zahiri
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Changying Zhao  (赵长颖)
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Hua Bao  (鲍 华)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hua Bao  (鲍 华).

Additional information

Foundation item: the National Natural Science Foundation of China (No. 51676121)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, S., Shao, C., Zahiri, S. et al. Thermal Transport in Nanoporous Yttria-Stabilized Zirconia by Molecular Dynamics Simulation. J. Shanghai Jiaotong Univ. (Sci.) 23, 38–44 (2018). https://doi.org/10.1007/s12204-018-1907-z

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12204-018-1907-z

Key words

CLC number

Search

Navigation