Abstract
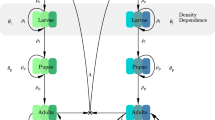
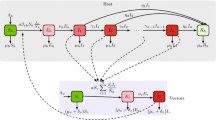
A host-vector disease model with insecticide resistance genes is proposed as a system of differential equations. The resistance-induced reproduction number \({\mathcal {R}}_e\) is determined and qualitative stabilities analysis are provided. We use the model to study the effects of insecticide resistance of vectors on the spread of the disease. The resistance-induced reproduction number \({\mathcal {R}}_e\) is compared with the basic reproduction number \(({\mathcal {R}}_0)\) in the absence of resistant strain to assess the effects of insecticide resistance.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Availability of data and material
Not applicable.
References
Berman, A., Plemmons, R.J.: Nonnegative Matrices in the Mathematical Sciences. SIAM, Philadelphia (1994)
Calisher, C.H.: Persistent emergence of dengue. Emerg. Infect. Dis. 11(5), 738 (2005)
Chanda, E., Thomsen, E.K., Musapa, M., Kamuliwo, M., Brogdon, W.G., Norris, D.E., Masaninga, F., Wirtz, R., Sikaala, C.H., Muleba, M., et al.: An operational framework for insecticide resistance management planning. Emerg. Infect. Dis. 22(5), 773 (2016)
Diekmann, O., Heesterbeek, J.A.P.: Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation, vol. 5. Wiley, Hoboken (2000)
Gubler, D.J.: Resurgent vector-borne diseases as a global health problem. Emerg. Infect. Dis. 4(3), 442 (1998)
Guo, H., Li, M.Y.: Impacts of migration and immigration on disease transmission dynamics in heterogeneous populations. Discrete Contin. Dyn. Syst. Ser. B 17(7), 2413–2430 (2012)
Harrus, S., Baneth, G.: Drivers for the emergence and re-emergence of vector-borne protozoal and bacterial diseases. Int. J. Parasitol. 35(11–12), 1309–1318 (2005)
Hirsch, W.M., Hanisch, H., Gabriel, J.P.: Differential equation models of some parasitic infections: methods for the study of asymptotic behavior. Commun. Pure Appl. Math. 38(6), 733–753 (1985)
Jacquez, J.A., Simon, C.P.: Qualitative theory of compartmental systems. SIAM Rev. 35(1), 43–79 (1993)
Koella, J., Antia, R.: Epidemiological models for the spread of anti-malarial resistance. Malaria J. 2(1), 3 (2003)
Kuniyoshi, M.L.G., dos Santos, F.L.P.: Mathematical modelling of vector-borne diseases and insecticide resistance evolution. J. Venom. Anim. Toxins Including Trop. Dis. 23(1), 34 (2017)
LaSalle, J.P.: The stability of dynamical systems, vol. 25. SIAM, Philadelphia (1976)
Mackinnon, M.: Drug resistance models for malaria. Acta Trop. 94(3), 207–217 (2005)
Molyneux, D.: Patterns of change in vector-borne diseases. Ann. Trop. Med. Parasitol. 91(7), 827–839 (1997)
Organization, W.H., et al.: A global brief on vector-borne diseases. Technical report, World Health Organization (2014)
Schmitz, S.F.H.: Effects of treatment or/and vaccination on hiv transmission in homosexuals with genetic heterogeneity. Math. Biosci. 167(1), 1–18 (2000)
Van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180(1–2), 29–48 (2002)
Varga, R.S.: Iterative Analysis. Springer, Berlin (1962)
Acknowledgements
Not applicable.
Funding
Not applicable.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The author declare that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Traoré, A. A theoretical assessment of the effects of vectors genetics on a host-vector disease. J. Appl. Math. Comput. 65, 793–811 (2021). https://doi.org/10.1007/s12190-020-01415-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12190-020-01415-7