Skip to main content

Advertisement

SpringerLink
Log in

Global stability analysis and optimal control of measles model with vaccination and treatment

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

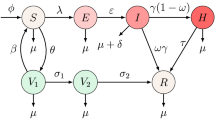
A transmission and control model for measles infection is presented. The model incorporates vaccinated individuals and the role of treatment for both exposed and infected individuals. We present two main equilibrium points (disease-free and endemic) with the analysis of their stability. The basic reproduction number is calculated and we find that when it is less than unity, the disease-free equilibrium point is both locally and globally stable which means the disease can be eradicated under such condition. When it is greater than one, the infection is uniformly persistent and the endemic equilibrium is globally stable. The sensitivity index of basic reproduction number to the parameters within the model is also determined. Further, by using Pontryagin’s minimum principle, the optimal control problem is constructed with three controls i.e. vaccination, treatment of exposed individuals and treatment of infected individuals. Finally, the numerical simulations are established and our results show that a combination of all three controls gives the best result in reducing the number of measles infected individuals. These results indicate that being vaccinated followed by some treatments for both exposed and infected individuals would make measles eradication more efficient.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Mazer, A., Sankalé, M.: Guide de médecine en Afrique et Océan Indien. EDICEF, Paris (1988)

    Google Scholar 

  2. Tessa, O.M.: Mathematical Model for Control of Measles by Vaccination, pp. 31–36. Department of Mathematics and Computer Science, Abdou Moumouni University, Niamey (2006)

    Google Scholar 

  3. Norrby, E., Oxman, M.N.: Measles virus. In: Fields, B.N., Knipe, D.M. (eds.) Virology, 2nd edn, pp. 1013–44. Raven Press Ltd, New York (1990)

    Google Scholar 

  4. Perry, R.T., Halsey, N.A.: The clinical significance of measles: a review. J. Infect. Dis. 189, S4–16 (2004)

    Article  Google Scholar 

  5. Panum, P.L.: Observations Made During the Epidemic of Measles on the Faroe Islands in the Year 1846. Delta Omega Society, Cleveland (1940)

    Google Scholar 

  6. Mossong, J., Muller, C.P.: Modelling measles re-emergence as a result of waning of immunity in vaccinated populations. Vaccine 21, 4597–4603 (2003)

    Article  Google Scholar 

  7. Ejima, K., Omori, R., Aihara, K., Nishiura, H.: Real-time investigation of measles epidemics with estimate of vaccine efficacy. Int. J. Biol. Sci. 8(5), 620–629 (2012)

    Article  Google Scholar 

  8. WHO, World Health Organization.: Measles. https://www.who.int/news-room/fact-sheets/detail/measles (2018). Accessed 12 March 2019

  9. Ciupe, S.M.: Modeling the dynamics of hepatitis B infection, immunity, and drug therapy. Immunol. Rev. 285, 38–54 (2018). https://doi.org/10.1111/imr.12686

    Article  Google Scholar 

  10. Viriyapong, R., Koompawan, G.: The impact of hygiene care and maternal immunity on stability behaviour of rotavirus infection model for children under the age of five in Thailand. Int. J. Math. Model. Numer. Optim. 8(4), 378–392 (2018). https://doi.org/10.1504/IJMMNO.2018.10015804

    Article  Google Scholar 

  11. Yosyingyong, P., Viriyapong, R.: Global stability and optimal control for a hepatitis B virus infection model with immune response and drug therapy. J. Appl. Math. Comput. 60(1–2), 537–565 (2019). https://doi.org/10.1007/s12190-018-01226-x

    Article  MathSciNet  MATH  Google Scholar 

  12. Elaiw, A.M., Almuallem, N.A.: Global properties of delayed-HIV dynamics models with differential drug efficacy in co-circulating target cells. Appl. Math. Comput. 265, 1067–1089 (2015). https://doi.org/10.1016/j.amc.2015.06.011

    Article  MathSciNet  MATH  Google Scholar 

  13. Jia, J., Xiao, J.: Stability analysis of a disease resistance SEIRS model with nonlinear incidence rate. Adv. Differ. Equ. 75, 13 (2018). https://doi.org/10.1186/s13662-018-1494-1

    Article  MathSciNet  MATH  Google Scholar 

  14. Rahman, G.U., Shah, K., Haq, F., Ahmad, N.: Host vector dynamics of pine wilt disease model with convex incidence rate. Chaos Solitons Fract. 113, 31–39 (2018). https://doi.org/10.1016/j.chaos.2018.05.010

    Article  MathSciNet  MATH  Google Scholar 

  15. Khan, S.A., Shah, K., Zaman, G., Jarad, F.: Existence theory and numerical solutions to smoking model under Caputo–Fabrizio fractional derivative. Chaos Interdiscip. J. Nonlinear Sci. 29(1), 013128 (2019). https://doi.org/10.1063/1.5079644

    Article  MathSciNet  MATH  Google Scholar 

  16. Hag, F., Shah, K., Rahman, G.U., Li, Y., Shazad, M.: Computational analysis of complex population dynamical model with arbitrary order. Complexity. 2018, Article ID 8918541, p. 8. https://doi.org/10.1155/2018/8918541 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  17. Okyere - Siabouh, S., Adetunde, I.A.: Mathematical model for the study of measles in cape coast metropolis. Int. J. Mod. Biol. Med. 4(2), 110–133 (2013)

    Google Scholar 

  18. Momoh, A.A., Ibrahim, M.O., Uwanta, J.I., Manga, S.B.: Mathematical model for control of measles epidemiology. Int. J. Pure Appl. Math. 87(5), 707–718 (2013)

    Article  Google Scholar 

  19. Garba, S.M., Safi, M.A., Usaini, S.: Mathematical model for assessing the impact of vaccination and treatment on measles transmission dynamics. Math. Methods Appl. Sci. 40, 6371–6388 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  20. Bolarin, G.: On the dynamical analysis of a new model for measles infection. Int. J. Math. Trends Technol. 7(2), 2231–5373 (2014)

    Article  Google Scholar 

  21. Edward, S., Raymond, K., Gabriel, K., Nestory, F., Godfrey, M., Arbogast, M.: A mathematical model for control and elimination of the transmission dynamics of measles. Appl. Comput. Math. 4(6), 396–408 (2015)

    Article  Google Scholar 

  22. Obumneke, C., Adamu, I.I., Ado, S.T.: Mathematical model for the dynamics of measles under the combined effect of vaccination and measles therapy. International Journal of Science and Technology 6(6), 862–874 (2017)

    Google Scholar 

  23. Beay, L.K.: Modelling the effects of treatment and quarantine on measles. In: AIP Conference Proceedings (2018)

  24. Ochoche, J.M., Gweryina, R.I.: A mathematical model of measles with vaccination and two phases of infectiousness. IOSR J. Math. (IOSR-JM) 10(1), 95–105 (2014)

    Article  Google Scholar 

  25. van den Driessche, P., Watmough, J.: Reproductive numbers and sub-threshold endemic equilibria for compartment models of disease transmission. Math. Biosci. 180, 29–48 (2002). https://doi.org/10.1016/S0025-5564(02)00108-6

    Article  MathSciNet  MATH  Google Scholar 

  26. LaSalle, J.P.: The Stability of Dynamical Systems. Regional Conference Series in Applied Mathematics. SIAM, Philadelphia (1976)

    Book  MATH  Google Scholar 

  27. Li, M.Y., Muldowney, J.S.: A geometric approach to global-stability problems. SIAM J. Math. Anal. 27(4), 1070–1083 (1996). https://doi.org/10.1137/S0036141094266449

    Article  MathSciNet  MATH  Google Scholar 

  28. Li, M.Y., Muldowney, J.S.: On Bendixson’s criterion. J. Differ. Equ. 106(1), 27–39 (1993). https://doi.org/10.1006/jdeq.1993.1097

    Article  MathSciNet  MATH  Google Scholar 

  29. Freedman, H.I., Ruan, S., Tang, M.: Uniform persistence and flows near a closed positively invariant set. J. Dyn. Differ. Equ. 6(4), 583–600 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  30. Butler, G., Freedman, H.I., Waltman, P.: Uniformly persistent systems. Proc. Am. Math. Soc. 96(3), 425–30 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  31. Samsuzzoha, M.D., Singh, M., Lucy, D.: Uncertainty and sensitivity analysis of the basic reproduction number of a vaccinated epidemic model of influenza. Appl. Math. Model. 37, 903–915 (2013). https://doi.org/10.1016/j.apm.2012.03.029

    Article  MathSciNet  MATH  Google Scholar 

  32. Ngoteya, F.N., Gyekye, Y.N.: Sensitivity analysis of parameters in a competition model. Appl. Comput. Math. 4(5), 363–368 (2015). https://doi.org/10.11648/j.acm.20150405.15

    Article  Google Scholar 

  33. Pontryagin, L.S.V., Boltyanskii, G.R., Gamkrelidze, V., Mishchenko, E.F.: The Mathematical Theory of Optimal Processes. Gordon and Breach Science Publishers, London (1986)

    MATH  Google Scholar 

  34. Peter, O., Afolabi, O., Victor, A., Akpan, C., Oguntolu, F.: Mathematical model for the control of measles. J. Appl. Sci. Environ. Manag. 22(4), 571–576 (2018)

    Google Scholar 

Download references

Acknowledgements

This work has been supported by Department of Mathematics, Faculty of Science, Naresuan University, Thailand.

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science, Naresuan University, Phitsanulok, 65000, Thailand

    Ratchada Viriyapong & Witchaya Ridbamroong

Authors
  1. Ratchada Viriyapong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Witchaya Ridbamroong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ratchada Viriyapong.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Viriyapong, R., Ridbamroong, W. Global stability analysis and optimal control of measles model with vaccination and treatment. J. Appl. Math. Comput. 62, 207–237 (2020). https://doi.org/10.1007/s12190-019-01282-x

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-019-01282-x

Keywords

Mathematics Subject Classification

Search

Navigation