Optimal bounds on codes for location in circulant graphs

Abstract

Identifying and locating-dominating codes have been studied widely in circulant graphs of type $C_{n}(1,2,3,\dots , r)$ over the recent years. In 2013, Ghebleh and Niepel studied locating-dominating and identifying codes in the circulant graphs $C_{n}(1,d)$ for $d = 3$ and proposed as an open question the case of $d > 3$. In this paper we study identifying, locating-dominating and self-identifying codes in the graphs $C_{n}(1,d)$, $C_{n}(1,d-1,d)$ and $C_{n}(1,d-1,d,d + 1)$. We give a new method to study lower bounds for these three codes in the circulant graphs using suitable grids. Moreover, we show that these bounds are attained for infinitely many parameters n and d. In addition, new approaches are provided which give the exact values for the optimal self-identifying codes in $C_{n}(1,3)$ and $C_{n}(1,4)$.

Appendix

The proof of the Theorem 10(ii):

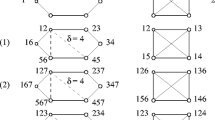
Let $d\ge 15$, $d\equiv 3 \pmod {6}$ and $n = 3d-9$. Notice that $n\equiv 0 \pmod {6}$. We divide the vertices of the circulant graph into three sections denoted by $A_{1}=\{0,1,2\dots , d-1\}$, $A_{2}=\{d,d + 1,\dots , 2d-1\}$ and $A_{3}=\{0,1,\dots ,n-1\}\setminus (A_{1}\cup A_{2})$. We will first consider the code

$$C_{d}=\{v\mid v\in (A_{1}\cup A_{3}), v\equiv 5 \pmod{6}\} \cup \{v\mid v\in A_{2}, v\equiv 0,4 \pmod{6}\}. $$

Using this code we can construct (by adding later two more codewords) an identifying code in $C_{n}(1,d-1,d,d + 1)$. The ratio $|C_{d}|/n$ tends to $2/9$ as d tends to infinity. First we exclude some ‘borderline’ vertices from the three sections and denote $A_{1}^{\prime }=A_{1}\setminus \{0,1,2,3,4,5,6,7,8,9,d-1\}$, $A_{2}^{\prime }=A_{2}\setminus \{d,2d-1\}$ and $A_{3}^{\prime }=A_{3}\setminus \{2d\}$. We consider the borderline vertices later. It is straightforward to check that the I-sets with regard to the code $C_{d}$ are as follows for $x\in A_{1}^{\prime }\cup A_{2}^{\prime }\cup A_{3}^{\prime }$:

Let us compare these I-sets (that is, when $x\in A_{1}^{\prime }\cup A_{2}^{\prime }\cup A_{3}^{\prime }$). Clearly, the I-sets of size one are distinguished. Consider then the I-sets of size two. In the tables above, one can found the distances $c_{1}-c_{2}$ of the codewords in $I(x)$ with $c_{1}>c_{2}$. If the distance is different, the I-sets cannot be the same. For those, which have the same distance, the $c_{1} \pmod {6}$ and $c_{2} \pmod {6}$ are different as shown in the table, and the I-sets again cannot be the same. Let us study the I-sets of size three then. According to the tables, the codewords in the I-sets are different modulo 6 unless $x\in A_{1}^{\prime }$ where $x\equiv 2 \pmod 6$ and $y\in A_{3}^{\prime }$ where $y\equiv 2\pmod {6}$. However, now $I(y)$ has distance 2 between its two largest codewords, but $I(x)$ has corresponding distance $d-10$. Consequently, I(x)≠I(y).

For the rest of the vertices (i.e., the borderline vertices $x\notin A_{1}^{\prime }\cup A_{2}^{\prime }\cup A_{3}^{\prime }$) we get the following I-sets: $I(0)=\{d + 1,2d-8,3d-10\}$, I(1) = {d + 1, 2d − 8}, $I(2)=\{d + 1,d + 3,2d-8,2d-6\}$, $I(3)=\{d + 3,2d-6\}$, $I(4)=\{5,d + 3,2d-6\}$, $I(5)=\{5\}$, $I(6)=\{5,d + 7,2d-2\}$, $I(7)=\{d + 7,2d-2\}$, $I(8)=\{d + 7,d + 9,2d-2\}$, I(9) = {d + 9}, $I(d-1)=\{2d-2,3d-10\},$$I(d)=\{d + 1,3d-10\}$, $I(2d-1)=\{2d-2\}$ and $I(2d)=\{d + 1\}$. It is straightforward to check (considering sizes of I-sets, codewords modulo 6 in I-sets and their distances) that we have exactly the following non-distinguished I-sets: $I(9)=I(d + 9)$, $I(d-1)=I(d-2)$, $I(d + 1)=I(2d)$ and $I(2d-2)=I(2d-1)$. We add two more codewords, namely, 0 and $2d$ to the code $C_{d}$ to avoid these same I-sets. Denote $C_{d}^{\prime }=C_{d}\cup \{0,2d\}$. We should bear in mind that if $I(C_{d};x)\neq I(C_{d};y)$, then also $I(C_{d}^{\prime };x)\neq I(C_{d}^{\prime };y)$. Now we have (with respect to $C_{d}^{\prime }$) that $2d\in I(9)\setminus I(d + 9)$, $0\in I(d-1)\setminus I(d-2)$, 2d ∈ I(2d − 1) ∖ I(2d − 2) and $0\in I(d + 1)\setminus I(2d)$. Therefore, $C_{d}^{\prime }$ is an identifying code and the proof is completed.