“This model will be a simplification and an idealization, and consequently a falsification. It is to be hoped that the features retained for discussion are those of greatest importance in the present state of knowledge.”—(Alan Turing, 1952)

“When we observe the environment, we necessarily do so on only a limited range of scales; therefore, our perception of events provides us with only a low-dimensional slice through a high-dimensional cake.”—(Simon Levin, 1992)

Introduction

Populations are inherently spatial, as their constituent individuals inhabit and move across the landscape in response to environmental and behavioral cues. We have long known that the distribution of individuals across a landscape and their dispersal—i.e. their population-level spatial structure—determines and constrains intra- and interspecific interactions (e.g., Skellam 1951; MacArthur and Wilson 1967; Levin 1974; Tilman and Kareiva 1997; Fagan et al. 1999). This spatial structure often arises from dispersal (e.g., Levins 1969; Gilpin and Hanski 1991; Hanski 1998, 1999; Bonsall et al. 2005; Schnell et al. 2013; Gibert 2016; Yeakel et al. 2018), habitat selection and suitability (MacArthur and Levins 1964; Rosenzweig 1981; Cody 1985; Hirzel et al. 2001; Brotons et al. 2004; Abrams 2007; Hirzel and Le Lay 2008), aggregation (Hassell and May 1974; Krause and Tegeder 1994; Levin 1994; May et al. 2016) or segregation of individuals (Recher 1966; Thiebot et al. 2012; Navarro et al. 2013), local environmental conditions (Pearson and Dawson 2003; Thuiller et al. 2004), local extinction (MacArthur and Wilson 1967; Levins 1969; Gilpin and Hanski 1991) as well as interspecific ecological interactions such as competition (Tilman 1994; Tilman et al. 1994; Amarasekare 2003; Amarasekare et al. 2004), predation (Bascompte et al. 2002; McCann et al. 2005; Amarasekare 2008), and facilitation (Choler et al. 2001; Stachowicz 2001; Boulangeat et al. 2012).

Ecological interactions and processes affect, and are affected by, the spatial structure of species. This interplay can change over time and influence the way individuals reproduce and die, which in turn alters population growth rates (e.g., Law et al. 2003). Indeed, spatial structure and dynamics as well as spatial heterogeneity often mediate coexistence over time (Levin 1974; Tilman 1994; Tilman and Kareiva 1997; Amarasekare and Nisbet 2001; Leibold et al. 2004), protect prey from their predators (e.g., Bowman and Harris 1980; Berkeley et al. 2004), or mediate predator–prey interactions (Hastings 1977, 1980, 1992; Holt 1984). The dispersal of individuals across the landscape therefore has myriad consequences for ecological dynamics and spatial pattern formation (Levins 1969, 1974; Hastings 1980; Gilpin and Hanski 1991; Holmes et al. 1994; Okubo and Levin 2001). Indeed, dispersal can maintain local populations above their extinction threshold in places where they would otherwise not be able to persist, a phenomenon known as ecological rescue (e.g., Gotelli 1991). Spatial structure and dynamics can also determine the way networks of interacting species are interconnected (McCann et al. 2005; Massol et al. 2011) and whether these complex networks can persist over time (Hassell et al. 1991; Amarasekare 2008; Massol et al. 2011; Gravel et al. 2011, 2016). Taken together, the consequences of spatial structure can directly influence species diversity over space and time (De Souza et al. 2014).

Populations often inhabit discrete areas of the landscape, or patches, where demographic processes occur within patches, and dispersal occurs between them. The movement of organisms between patches leads to local differences in colonization and extinction rates, which can both influence the spatial distribution of a species over time (Levins 1969; Gilpin and Hanski 1991; Hanski and Mononen 2011). Seminal work by MacArthur and Wilson (1967) showed that the distance between patches (for example, between islands and a mainland) influences diversity. In fact, the study and understanding of patch dynamics gave rise to fundamental and long-standing ecological theories, including (Hanski 1998, 1999), metacommunity dynamics (Leibold et al. 2004; Chisholm and Gonzalez 2010; Pillai et al. 2010; Carrara et al. 2012), and even metaecosystems (Loreau et al. 2003; Massol et al. 2011).

Disregarding spatial structure can be detrimental to our understanding of ecological processes. Indeed, disciplines of ecology that have historically overlooked spatial structure, such as the food web theory, are now working toward incorporating spatial processes in such a way to further investigate and understand the structure and stability of networks of interacting species and food webs (e.g., McCann et al. 2005; Holland and Hastings 2008; Massol et al. 2011; Gravel et al. 2011, 2016; Albouy et al. 2014). Recent work has shown that the topology of food webs strongly depends on the spatial structure of their constituent species (Massol et al. 2011; Gravel et al. 2011). The movement of even a small fraction of such species, such as top predators, can strongly influence species persistence within food webs (Gravel et al. 2011; Pillai et al. 2011), as well as food web stability (McCann et al. 2005), i.e., the tendency of the system to return to a steady state after a small perturbation. Indeed, the spatial coupling of food webs within metacommunities (Massol et al. 2011) or metaecosystems (Gravel et al. 2016) can either positively or negatively impact stability, which has myriad consequences for our understanding of how these complex networks of interacting species persist in nature, directly addressing a long-standing debate in ecology (May 1972; McCann 2000).

The spatial structure of interacting populations can also determine the pace and outcome of tcoevolutionary processes (Nuismer et al. 1999, 2000, 2003; Gomulkiewicz et al. 2000; Doebeli and Dieckmann 2003; Nuismer 2006; Gandon and Nuismer 2009; Gibert et al. 2013; Raimundo et al. 2014; Yeakel et al. 2018). Not only does the topology of spatial networks of co-occurrence matter, so does the number of connections between sites, as well as the distribution of sites where selection is reciprocal across the landscape (i.e., coevolutionary hotspots, Nuismer et al. 1999; Gomulkiewicz et al. 2000; Gibert et al. 2013). Many empirical tests of these ideas have shown spatially structured evolutionary and coevolutionary dynamics between parasites and hosts as well as bacteria and phages (Greischar and Koskella 2007; Carlsson-Granér and Thrall 2015; Penczykowski et al. 2016; Fronhofer and Altermatt 2017), with important consequences for the dispersal of infectious diseases across landscapes (Levin and Pimentel 1981). Indeed, the role of spatially structured ecological processes in mediating the evolution and epidemiology of diseases was acknowledged very early (Levin and Pimentel 1981) and has since become a central tenet of disease ecology (Holdenrieder et al. 2004; Biek and Real 2010).

Space therefore plays a central role in mediating ecological dynamics across scales, from individuals to ecosystems and from microbes to macrobes. Understanding how the spatial structure of populations or collections of interacting populations, constrain, facilitate, or determine ecological dynamics, however, is still an active area of research, due to the complex nature of the problem and its profound implications. Here, we seek to revisit and build upon seminal work by Levin (1974), to explore the importance of dispersal-induced instabilities for population dynamics, species persistence, and pattern formation in space. The first section of this paper reviews some of the fundamentals of a family of models that incorporates space in ecological dynamics. The second section revisits Levin’s work where it was shown that the spatial structure of competing species ensures stable coexistence. We then build upon these results to ask whether such phenomena hold for larger, more complex spatial structures. Lastly, we explore the role that migration-induced instabilities play in determining predator–prey persistence over time as well as the onset of pattern formation.

Levin’s seminal paper was not the first in examining the role of space in ecological dynamics: the role of dispersal and its ecological effects had first been acknowledged in the 1950s (Skellam 1951) and explored by others (Cohen 1970; Levins and Culver 1971; Horn and MacArthur 1972) based on earlier work by Alan Turing (1952) and Othmer and Scrivens (1972). However, Levin highlighted the potentially important role that spatially induced instabilities may play in ecological dynamics. By revisiting Levin’s work, we thus seek to explore and contrast the role of dynamic stability in ecological dynamics: we show that although dynamic stability is positively associated with persistence in nonspatial systems, its effect can be more multifaceted in spatially explicit scenarios, having both positive and negative effects on species persistence and community diversity.

Generalities of spatial ecological models

A number of suitable approaches can be introduced to explore the effects of spatial structure on population dynamics. For example, the patch dynamics framework can be used to determine site occupancy as a function of processes occurring over long time scales, such as colonization and extinction (e.g., Levins 1969; Hanski 1998, 1999), while disregarding changes in population abundances over time. Levin’s (1974) approach built upon previous theoretical work that quantified how short-term processes, such as reproduction and mortality, influenced population dynamics within sites connected by dispersal. As opposed to patch dynamics, this approach tracked changes in population abundances in addition to changes in patch occupancy to examine the larger-scale effects of both intra- and, eventually, interspecific interactions. However, there are multiple ways to model these shorter-term processes in a spatially explicit framework. A common approach involves using reaction–diffusion equations, which have traditionally been used to study and understand the dynamics of quantities that change over both space and time, like chemical reactions and morphogen diffusion (Turing 1952; Othmer and Scriven 1971), or in this case, interacting and dispersing species.

Reaction–diffusion equations keep track of two species interacting over a continuous landscape, such that the population density of both species, N1 and N2, is a function of time and space, N1(t, X) and N2(t, X), with X being an n-dimensional vector (i.e., for a unidimensional space, X = (x), for a two-dimensional space, X = (x, y), and so forth). Here and henceforth, we write only N1 and N2 for simplicity. Intra- and interspecific interactions for species N1 and N2 are determined by the functions f(N1, N2) and g(N1, N2), respectively, and movement across the continuous landscape is assumed to be governed by passive diffusion. In such a case, movement is controlled by the diffusion coefficient, D, that controls the magnitude of the rate of movement for both interacting species, and the Laplace operator, ∇2, defined as ∇2Ni = ∂2Ni/∂X2. The Laplace operator quantifies the change in density due to the movement of species from regions where densities are high to regions where densities are low. For example, in two-dimensional space (X = (x, y)), the Laplacian term is:

$$ {\nabla}^2{N}_i=\frac{\partial^2{N}_i}{\partial {\boldsymbol{X}}^2}=\frac{\partial^2{N}_i}{\partial {x}^2}+\frac{\partial^2{N}_i}{\partial {y}^2}. $$
(1)

The governing equations that describe the temporal evolution of the system over time and space then are,

$$ \frac{\partial {N}_1}{\partial t}=f\left({N}_1,{N}_2\right)+{D}_1{\nabla}^2{N}_1 $$
(2)
$$ \frac{\partial {N}_2}{\partial t}=g\left({N}_1,{N}_2\right)+{D}_2{\nabla}^2{N}_2. $$
(3)

which incorporate both changes in population growth rate due to ecological interactions (functions f and g) and due to dispersal (D and the Laplace operator). This framework has been used to explore the importance of dispersal across space to understand species distributions, persistence, and interspecific interactions (e.g., Gurney and Nisbet 1975; Hastings 1992; Morris 1993; Lewis and Murray 1993; Holmes et al. 1994; White et al. 1996; Okubo and Levin 2001; McKenzie et al. 2012; Potts et al. 2016).

To introduce Levin’s work, we discretize space into a collection of patches connected by migration, much in the way of classic patch dynamics, in which case the model in (2) and (3) becomes:

$$ \frac{\mathrm{d}{N}_{1,i}}{\mathrm{d}t}=f\left({N}_{1,i},{N}_{2,i}\right)+D{\sum}_{j=1}^n\left({N}_{1,j}-{N}_{1,i}\right) $$
(4)
$$ \frac{\mathrm{d}{N}_{2,i}}{\mathrm{d}t}=g\left({N}_{1,i},{N}_{2,i}\right)+\varepsilon D{\sum}_{j=1}^n\left({N}_{2,j}-{N}_{2,i}\right),\mathrm{for}\ i=1,\dots, n. $$
(5)

If we define D as the rate of dispersal for species N1, ε represents how much species N2 moves with respect to species N1: if ε > 1, then N2 moves at a higher rate than does N1, and if 0 < ε < 1, the opposite is true. The discrete-space model approaches the continuous-space model when n is large and every patch is connected to each other (Nakao and Mikhailov 2010).

The connections between patches on a landscape (i.e., which patches are connected to one another) can be summarized by the adjacency matrix (A), where Aij—the elements of the matrix—are equal to 1 whenever patches i and j are connected by dispersal, and 0 otherwise. We set the diagonal elements of the matrix as Aii = 0. Incorporating this matrix notation, the system in (4) and (5) can be rewritten as:

$$ \frac{\mathrm{d}{N}_{1,i}}{\mathrm{d}t}=f\left({N}_{1,i},{N}_{2,i}\right)+D{\sum}_{j=1}^n{A}_{ij}\left({N}_{1,j}-{N}_{1,i}\right) $$
(6)
$$ \frac{\mathrm{d}{N}_{2,i}}{\mathrm{d}t}=g\left({N}_{1,i},{N}_{2,i}\right)+D{\sum}_{j=1}^n{A}_{ij}\left({N}_{2,j}-{N}_{2,i}\right),\mathrm{for}\ i=1,\dots, n, $$
(7)

or equivalently,

$$ \frac{\mathrm{d}{N}_{1,i}}{\mathrm{d}t}=f\left({N}_{1,i},{N}_{2,i}\right)+D{\sum}_{j=1}^n{L}_{ij}{N}_{1,j} $$
(8)
$$ \frac{\mathrm{d}{N}_{2,i}}{\mathrm{d}t}=g\left({N}_{1,i},{N}_{2,i}\right)+D{\sum}_{j=1}^n{L}_{ij}{N}_{2,j},\mathrm{for}\ i=1,\dots, n, $$
(9)

where Lij are the elements of the Laplacian matrix of the underlying spatial network of patches. The Laplacian matrix is defined as Lij = Aij − kiδij, where \( {k}_i=\sum \limits_{j=1}^n{A}_{ij} \) (the degree or number of connections of patch i), and δij is the Kronecker delta function, such that δij = 0 for i ≠ j, and 1 otherwise. Notice how in the discrete version of the model, the Laplacian matrix plays a similar role as the Laplacian operator in the reaction–diffusion version of the model in Eqs. (2) and (3).

This general model determines the densities of species N1 and N2 over time across n patches. In the following section, we will illustrate some of the biological insights gained by analyzing such a model based on the results in Levin (1974), where species coexistence and pattern formation are explored in a spatial context.

Stability-mediated coexistence

The model

Levin’s 1974 paper showed that two species that cannot coexist locally can in fact coexist globally when dispersal across an explicit landscape is taken into account. In what follows, we recapitulate Levin’s original argument and examples, discuss the importance of stability for the coexistence of spatially structured competing species, and explore whether these results hold for more complex underlying spatial configurations.

Following Levin’s original argument, let us focus on a simple case of the model described in the previous section, where two species, N1 and N2, inhabit two sites and compete for resources. To follow Levin’s notation, we call the classic intrinsic growth rate parameter θ, (rather than r), and the effects of intra- and interspecific competition on growth are determined by a and b, respectively. Taken together, the dynamical system is written as

$$ \frac{\mathrm{d}{N}_{1,i}}{\mathrm{d}t}={N}_{1,i}\left(\theta -a{N}_{1,i}-b{N}_{2,i}\right)+D{\sum}_{j=1}^{n=2}{A}_{ij}\left({N}_{1,j}-{N}_{1,i}\right) $$
(10)
$$ \frac{\mathrm{d}{N}_{2,i}}{\mathrm{d}t}={N}_{2,i}\left(\theta -b{N}_{1,i}-a{N}_{2,i}\right)+D{\sum}_{j=1}^{n=2}{A}_{ij}\left({N}_{2,j}-{N}_{2,i}\right),\mathrm{for}\ i=1,2. $$
(11)

The model in (10) and (11) is equivalent to the classic two-site Lotka–Volterra competition framework whenever a = αiir/K and b = αijr/K (where αij are competition coefficients, and K is the carrying capacity of both species across sites).

When dispersal does not occur between sites, such that D = 0, the model has one trivial steady-state solution at N1 = 0 and N2 = 0 in all sites and three nontrivial steady-state solutions: 1) N1 = 0 and = θ/a, 2) N1 = θ/a and N2 = 0, and the single internal steady state 3) N1 = θ/(a + b) and N2 = θ/(a + b). However, only steady states 1) and 2) are stable, resulting in the competitive exclusion of one competitor or the other, and no stable coexistence steady state is possible. A key result of this spatially explicit framework is that when there is dispersal (D > 0), the system also has an internal and stable solution of the form:

$$ {\overline{N}}_{11}={\overline{N}}_{22}=\frac{\theta -2\mathrm{D}}{2a}-\frac{1}{2a}\sqrt{\left(\theta -2D\right)\left(\theta -2D\frac{b+a}{b-a}\right)} $$
(12)
$$ {\overline{N}}_{12}={\overline{N}}_{21}=\frac{\theta -2\mathrm{D}}{2a}+\frac{1}{2a}\sqrt{\left(\theta -2D\right)\left(\theta -2D\frac{b+a}{b-a}\right),} $$
(13)

where \( {\overline{N}}_{ij} \) represent steady-state abundances. This single result testifies to the importance of considering the role of space in species competitive interactions: without dispersal, coexistence does not occur, whereas when dispersal is allowed, coexistence is stable under the condition that D is small. In the following section, we examine this caveat in more detail.

Stability in the two-patch model

To assess the local stability of the two-competitor, two-patch dynamical system evaluated at a particular steady state, we apply a small perturbation x(t) to the steady-state population density of each species in each site, e.g., \( {N}_{1,i}(t)={\overline{N}}_{1,i}+{x}_{1,i}(t) \). Rearranging, the perturbation over time is then

$$ \boldsymbol{x}(t)=\left(\begin{array}{c}{N}_{11}(t)-{\overline{N}}_{11}\\ {}{N}_{21}(t)-{\overline{N}}_{21}\\ {}\begin{array}{c}{N}_{22}(t)-{\overline{N}}_{22}\\ {}{N}_{12}(t)-{\overline{N}}_{12}\end{array}\end{array}\right), $$
(14)

and the reason for swapping the positions of N22 and N12 is an important detail that will be clear shortly. Linearizing the system of equations about the steady state and dropping higher order terms (i.e., Taylor-expanding about the steady state), we obtain the following system of equations in matrix form:

$$ \frac{\mathrm{d}\boldsymbol{x}(t)}{\mathrm{d}t}=\boldsymbol{Jx}(t), $$
(15)

where J is the Jacobian matrix, the elements of J are defined as \( {\boldsymbol{J}}_{ij}={\left.\frac{\delta \frac{{\mathrm{d}N}_i}{\mathrm{d}t}}{\delta {\boldsymbol{V}}_j}\right|}_{{\overline{N}}_{1,k},{\overline{\ N}}_{2,k}} \) with V = (N11, N21, N22, N12), and where the expression is evaluated at the internal steady state (denoted by the \( {\left.\right|}_{{\overline{N}}_{1,k},{\overline{\ N}}_{2,k}} \), notation).

If at least one eigenvalue of the Jacobian is positive, the perturbations x(t) grow exponentially over time and the steady-state solution is unstable. If all eigenvalues are negative, the perturbations decay exponentially and the steady-state solution is stable. In our model, the Jacobian is:

$$ \boldsymbol{J}=\left(\begin{array}{cccc}\theta -2a{\overline{N}}_{11}-b{\overline{N}}_{21}-D& -b{\overline{N}}_{11}& 0& D\\ {}-b{\overline{N}}_{21}& \theta -b{\overline{N}}_{11}-2a{\overline{N}}_{21}-D& D& 0\\ {}0& D& \theta -b{\overline{N}}_{12}-2a{\overline{N}}_{22}-D& -b{\overline{N}}_{22}\\ {}D& 0& -b{\overline{N}}_{12}& \theta -2a{\overline{N}}_{12}-b{\overline{N}}_{22}-D\end{array}\right) $$
(16)

Finding the eigenvalues of large matrices becomes computationally expensive and analytically intractable as the number of sites and/or species grows. Even for a relatively simple model like ours, solutions of an algebraic equation of order 4 are required, which are complicated but tractable, though analytically intractable for Jacobians larger than order 5. It is thus beneficial to simplify such calculations. Levin accomplished this by building upon previous literature showing that the full Jacobian of the system, J, can be rewritten as a function of the Jacobian of each local patch, Jlocal and the adjacency matrix of the underlying spatial network of sites. Notice the two local Jacobians, when linearized based on the order established in Eq. (12) (thus swapping the order of N22 and N12), are the same:

$$ {\displaystyle \begin{array}{c}{J}_{\mathrm{local}}=\left(\begin{array}{cc}\theta -2a{\overline{N}}_{11}-b{\overline{N}}_{21}-D& -b{\overline{N}}_{11}\\ {}-b{\overline{N}}_{21}& \theta -b{\overline{N}}_{11}-2a{\overline{N}}_{21}-D\end{array}\right)\\ {}=\left(\begin{array}{cc}\theta -b{\overline{N}}_{12}-2a{\overline{N}}_{22}-D& -b{\overline{N}}_{22}\\ {}-b{\overline{N}}_{12}& \theta -2a{\overline{N}}_{12}-b{\overline{N}}_{22}-D\end{array}\right),\end{array}} $$
(17)

because \( {\overline{N}}_{11}={\overline{N}}_{22} \) and \( {\overline{N}}_{12}={\overline{N}}_{21} \) (Eqs. (12) and (13)). We can thus rewrite (16) as:

$$ \boldsymbol{J}={\boldsymbol{I}}_2\otimes {\boldsymbol{J}}_{\mathrm{local}}+D\boldsymbol{A}\otimes \boldsymbol{A}\kern0.5em , $$
(18)

where A is the adjacency matrix associated with the underlying spatial network of patches,

$$ \boldsymbol{A}=\left(\begin{array}{cc}0& 1\\ {}1& 0\end{array}\right), $$
(19)

I2 is the 2 × 2 identity matrix,

$$ {\boldsymbol{I}}_2=\left(\begin{array}{cc}1& 0\\ {}0& 1\end{array}\right), $$
(20)

and ⊗ is the Kronecker product, where, if we have two matrices α2 × 2 and β2 × 2, the Kronecker product between the two is:

$$ \boldsymbol{\alpha} \otimes \boldsymbol{\beta} =\left(\begin{array}{cc}{\alpha}_1& {\alpha}_2\\ {}{\alpha}_3& {\alpha}_4\end{array}\right)\otimes \left(\begin{array}{cc}{\beta}_1& {\beta}_2\\ {}{\beta}_3& {\beta}_4\end{array}\right)=\left(\begin{array}{cc}\begin{array}{cc}{\alpha}_1{\beta}_1& {\alpha}_1{\beta}_2\\ {}{\alpha}_1{\beta}_3& {\alpha}_1{\beta}_4\end{array}& \begin{array}{cc}{\alpha}_2{\beta}_1& {\alpha}_2{\beta}_2\\ {}{\alpha}_2{\beta}_3& {\alpha}_2{\beta}_4\end{array}\\ {}\begin{array}{cc}{\alpha}_3{\beta}_1& {\alpha}_3{\beta}_2\\ {}{\alpha}_3{\beta}_3& {\alpha}_3{\beta}_4\end{array}& \begin{array}{cc}{\alpha}_4{\beta}_1& {\alpha}_4{\beta}_2\\ {}{\alpha}_4{\beta}_3& {\alpha}_4{\beta}_4\end{array}\end{array}\right), $$
(21)

and D is the movement rate. Whenever a Jacobian can be written as in Eq. (18), where the matrices I2 and A are Hermitian (i.e., the matrix equals its complex conjugate transpose), the eigenvalues of (18) are equal to the eigenvalues of:

$$ {\boldsymbol{J}}_{\mathrm{local}}+{\lambda}_iD\boldsymbol{A},i=1,2 $$
(22)

where λ1, 2 are the eigenvalues of the adjacency matrix A (Friedman 1956). In our model, the eigenvalues of the Jacobian, thus, become the eigenvalues of

$$ {\boldsymbol{J}}_{\mathrm{local}}\pm D\boldsymbol{A}=\left(\begin{array}{cc}\theta -2a{\overline{N}}_{11}-b{\overline{N}}_{21}-D& -b{\overline{N}}_{11}\pm D\\ {}-b{\overline{N}}_{21}\pm D& \theta -b{\overline{N}}_{11}-2a{\overline{N}}_{21}-D\end{array}\right), $$
(23)

given that the eigenvalues of A (as in Eq. 19) are 1 and − 1. This reorganization and substitution greatly simplifies the task of analyzing the original Jacobian, by collapsing a system of order 4 to a system of order 2. Notice that if we had chosen an order different than that in Eq. (14), we would not have been able to use the equality in Eq. (18), and would have had to resort to analyzing the matrix in Eq. (16), which is much more cumbersome.

We can now evaluate the conditions for coexistence, which occurs whenever the steady-state solution in (12) and (13) is stable. The single internal steady state is stable when Trace(Jlocal ± DA) < 0 and Det(Jlocal ± DA) > 0, where:

$$ \mathrm{Trace}\left({\boldsymbol{J}}_{\mathrm{local}}\pm D\boldsymbol{A}\right)=\theta -2a{\overline{N}}_{11}-b{\overline{N}}_{21}-D+\theta -b{\overline{N}}_{11}-2a{\overline{N}}_{21}-D $$
(24)
$$ \mathrm{Det}\left({\boldsymbol{J}}_{\mathrm{local}}\pm D\boldsymbol{A}\right)=\left(\theta -2a{\overline{N}}_{11}-b{\overline{N}}_{21}-D\right)\left(\theta -b{\overline{N}}_{11}-2a{\overline{N}}_{21}-D\right)-\left(-b{\overline{N}}_{11}\pm D\right)\left(-b{\overline{N}}_{21}\pm D\right). $$
(25)

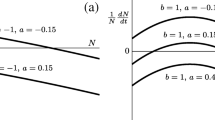
By substituting the steady state in Eqs. (12) and (13) into Eqs. (24) and (25), we can see that Trace(Jlocal ± DA) < 0 if and only if \( D<\frac{\theta }{2}\left(\frac{b-a}{b+2a}\right) \), and Trace(Jlocal ± DA) > 0 if and only if \( D>\frac{\theta }{2}\left(\frac{b-a}{b+2a}\right) \) (see Levin 1974, Appendix 2). In other words, stable coexistence is feasible as long as dispersal across sites is low and smaller than \( \frac{\theta }{2}\left(\frac{b-a}{b+2a}\right) \) (Fig. 1a). If D is too large, the two sites are effectively behaving as one, and as we saw for a single site, coexistence is no longer feasible (Fig. 1b). This result emphasizes the importance of space and dispersal across sites to ensure coexistence of species that would otherwise not coexist. But do Levin’s results hold in larger, more complex spatial structures?

Fig. 1
figure 1

a Both species coexist at low movement rates (D = 0.11). b One species goes extinct at higher movement rates (D = 0.15). All other parameters as: θ= 3, a= 1.1, b= 1.5

Full size image

Stability within a complex spatial network

The spatial structure of ecological systems is, however, much more complex in nature than that considered by Levin’s original model. In what follows we show under which conditions does Levin’s result holds in systems with a larger number of sites and with complex spatial structure. We will also show that—in some cases—coexistence can be predicted a priori by knowing only the topology of the spatial network, even without having a full picture of the underlying population dynamics.

The competition model for n patches can be written as:

$$ \frac{\mathrm{d}{N}_{1,i}}{\mathrm{d}t}={N}_{1,i}\left(\theta -a{N}_{1,i}-b{N}_{2,i}\right)+D{\sum}_{j=1}^n{A}_{ij}\left({N}_{1,j}-{N}_{1,i}\right) $$
(26)
$$ \frac{\mathrm{d}{N}_{2,i}}{\mathrm{d}t}={N}_{2,i}\left(\theta -b{N}_{1,i}-a{N}_{2,i}\right)+D{\sum}_{j=1}^n{A}_{ij}\left({N}_{2,j}-{N}_{2,i}\right),\kern0.75em \mathrm{for}\ i=1,\dots, n, $$
(27)

which, as we have shown, can be rewritten as a function of the Laplacian matrix, such that:

$$ \frac{\mathrm{d}{N}_{1,i}}{\mathrm{d}t}={N}_{1,i}\left(\theta -a{N}_{1,i}-b{N}_{2,i}\right)+D{\sum}_{j=1}^n{L}_{ij}{N}_{1,j} $$
(28)
$$ \frac{\mathrm{d}{N}_{2,i}}{\mathrm{d}t}={N}_{2,i}\left(\theta -b{N}_{1,i}-a{N}_{2,i}\right)+D{\sum}_{j=1}^n{L}_{ij}{N}_{2,j},\kern0.75em \mathrm{for}\ i=1,2,\dots, n. $$
(29)

The Laplacian matrix, L, is particularly useful as many of its algebraic properties are directly linked to the structural properties of the underlying network of patches, and have consequences for the dynamic properties of populations interacting on the spatial network.

If we define Λ as the spectrum of L, such that, Λ = (Λ0, Λ1, …, Λn) with Λi being the eigenvalues of L (and listed such that Λ0< Λ1< … < Λn), the number of eigenvalues equal to zero equals the number of connected components of the network (or number of independent subnetworks, Barrat et al. 2008). A network made of a single connected component has Λ0 = 0, a network with two connected components, has Λ0 = 0 and Λ1 = 0, and so forth. Moreover, the magnitude of the ratio of the second smallest eigenvalue to the largest (e.g., Λ1/Λn in a network with one connected component—henceforth described as the Laplacian eigenratio) is directly linked to the propensity of a network to exhibit fully synchronized dynamics (Barrat et al. 2008). In fact, the Laplacian eigenratio has been successfully used before to understand and predict ecological dynamics in riverine networks (Yeakel et al. 2014) and spatially structured coevolutionary dynamics (Gibert et al. 2013). However, the link between the Laplacian eigenratio and the dynamic properties of the network typically applies to dynamic oscillators of some kind (predator–prey dynamics, matching alleles model, etc), and it is unclear whether such results could also apply to the system presented in Eqs. (26)–(27). We thus examine: 1) whether Levin’s principal findings extend to larger, more complex networks, and 2) whether we can predict some of the observed behavior of the model using the Laplacian eigenratio, which is a function of spatial structure, and thus independent of the underlying dynamics. Because the spatial structure of interacting populations is easier to quantify than the constraints that determine the dynamics for most populations, having a predictor of dynamics that does not require knowledge of the underlying metapopulation dynamics could be important for conservation biologists and managers.

We simulated the resource–consumer system in Eqs. (26)–(27) across spatial networks with an increasing number of patches, with spatial structures determined by the Barabási–Albert model (such that the spatial networks have a power law degree distribution, where each network is formed by a small number of highly connected sites, or hubs, connected to a larger number of peripheral sites with fewer connections, Barabási and Albert 1999). We also examined networks with an increasing average number of connections (average node degree = 1, 2, and 10) and for increasing dispersal between populations (D = 0.2, 0.35, 0.5). Because the underlying network is just one possible realization of a stochastic algorithm, we obtained 1000 network replicates where the underlying spatial structure was randomized for each combination of patch number and movement rate D (patch number ranged from 15 to 65). To assess coexistence, we measured the number of extinctions of local populations that occurred over each of the n patches, and averaged the total number of extinctions across replicates. Populations were considered to go extinct if local abundances fell below 10−4. Because coexistence is only possible when the steady-state solutions are stable, changes in the number of extinctions points to changes in stability. To test whether we can predict the behavior of the system using only the structural features of the underlying spatial network, we also calculated the Laplacian eigenratio for each of the replicates and compared this measure to the average number of extinctions.

We observed that, while Levin’s result holds—namely, as D increases, the likelihood of species coexisting decreases—the system behaves differently as the average node degree of the network decreases (patches become more isolated, and those at the periphery are attached to a fewer number of hubs). At the extreme end, where the average node degree equals one, the spatial network is shaped very much like a river, where populations in different tributaries can only reach each other by traversing those few nodes that serve as confluence points (Yeakel et al. 2014; Moore et al. 2015; Terui et al. 2018). We find that the potential for coexistence can increase with the number of patches, but only if the average node degree is low, and this effect is particularly strong for networks with riverine topologies. Moreover, we find that river-like networks with a larger number of patches can facilitate coexistence for a greater range of D (Fig. 2a). This result indicates that species competing on river-like networks may be less prone to extinction, even if their dispersal rates are exaggerated, supporting recent empirical observations of river metapopulations (Terui et al. 2018). In contrast, for networks with higher average node degree, the potential for coexistence declines with an increasing number of patches but is relatively constant for values of D above a minimum threshold, below which coexistence is feasible (Fig. 2b, c). In such cases, and mirroring Levin’s original finding for the effects of increasing diffusion within the two-site model, a greater number of interconnections between sites serves to homogenize local interactions, such that the system begins to operate as a single patch, and the potential for coexistence begins to erode.

Fig. 2
figure 2

a Top: spatial network for an average node degree equal to 1. Middle: number of extinctions (low = blue, high = yellow) for all combinations of the number of available patches and migration rate D. Bottom: time series for all species across all sites (color code as in Fig. 1) for the combination of number of patches and migration rate marked as an asterisk (namely, 50 patches, D = 0.05). b As in a but for an average node degree equal to 2. c As in a and b but for an average node degree equal to 10. All the other parameters as in Fig. 1

Full size image

When the node degree is low and connectivity is limited (e.g., Fig. 2a), the Laplacian eigenratio is predictive of coexistence. In general, a lower eigenratio means the network is closer to having disconnected components; however, there is no unique match between network structure and eigenratio value. Conversely, larger eigenratios suggest greater overall connectivity and an increased likelihood for exhibiting synchronous dynamics across sites. We observe that, as the eigenratio increases, the number of extinctions increases and then plateaus, and this pattern becomes more robust for larger values of D (Fig. 3), thus mirroring what we observe in Fig. 2a. This relationship disappears when dispersal rates are low (Fig. 3a, green). Our results show that a strong relationship between the Laplacian ratio and the number of extinctions emerges as the interconnectivity between sites grows and that this relationship is insensitive to dispersal rates (Fig. 3b, c). For populations in nonriverine systems, where node degree is low and connectivity is limited, these relationships suggest that a great deal about dynamics can be inferred directly from the spatial structure of interacting populations, even if the details of those dynamics are unknown. It has been suggested, however, that most metapopulations are more likely to occur as riverine networks—even those that are not constrained by rivers (Fronhofer and Altermatt 2017). That the interplay between structure and dynamics follows remarkably different rules when the spatial network is riverine (Figs. 2a and 3a) hints at potentially important future areas of research. Moreover, one major caveat of the present approach is the assumption of equal dispersal rates among all patches. While this assumption is commonplace, it is also most likely not to hold in nature. As such, assessing the effects of changes in these assumptions could be an interesting future avenue for research.

Fig. 3
figure 3

Number of extinctions against the Laplacian eigenratio (Λ1/Λn) of the underlying network for increasing movement rates for an underlying spatial network with average node degree equal to 1 (a), equal to 2 (b), or equal to 10 (c). All the other parameters as in Fig. 2

Full size image

Interestingly, while we show that is possible to predict dynamical outcomes in some cases if we know only the structure of the spatial network, the contrary is not always true. Previous work has shown that if our knowledge is limited to the dynamics of a spatially distributed system of interacting populations, it is not generally possible to predict the structure of the network upon which such dynamics occur (Gilarranz et al. 2014). This asymmetry in the information we obtain from the network versus the information obtained from the dynamic system likely has important consequences for the capacity to infer network from process and process from network, particularly in the face of imperfect information (Novak et al. 2011).

Instability-mediated spatial pattern formation

We have explored Levin’s finding that coexistence between pairs of competing species is ensured in space whenever steady-state solutions are stable and that, in some cases, dispersal-mediated coexistence extends to larger, more complex spatial networks. In this section, we expand upon Levin’s results to show that diffusion-mediated instability, rather than stability, can also factor into determining the persistence of populations over time. Mirroring Levin’s paper, we now examine the onset of spatial instabilities and their role in generating spatial pattern formation in a consumer–resource (or predator–prey) system and to what extent these dynamics can influence important statistical properties of populations such as variance-dampening portfolio effects (Moore et al. 2010, 2015; Yeakel et al. 2014; Anderson et al. 2015) and their impact on extinction risk.

If we consider a system, where space is continuous and interacting species move across the landscape (such as that defined in Eqs. (1) and (2)), spatial pattern formation—defined as the onset of heterogeneous steady-state abundances over space—can emerge (e.g., Baurmann et al. 2007). The potential ecological importance of those situations in which pattern formation can be observed has been explored elsewhere (e.g., Holmes et al. 1994). One mechanism for the creation of a spatial pattern in the densities of interacting species is dispersal-induced instability, that is, the process whereby spatial movement destabilizes an otherwise stable steady state. In such a scenario, we say the system undergoes a diffusion-induced instability, or crosses a Turing bifurcation, named after the mathematician Alan Turing, who first described the conditions under which spatial pattern formation could occur for a system of diffusing chemical morphogens (Turing 1952). In what follows, we consider a consumer–resource model and examine under what circumstances pattern formation may arise in a two-species system interacting across a discrete landscape of habitat patches, and discuss some of the consequences of crossing the Turing bifurcation for species persistence. We begin by discussing the general conditions under which Turing bifurcations occur, revisit Levin’s work from that perspective, and conclude by exploring broader consequences for large complex spatial networks based on recent theoretical studies on pattern formation in discrete landscapes.

A general multipatch model

Let us consider a consumer–resource model where both interacting species move at rates DC and DR, respectively, over the landscape. Following previous work (Nakao and Mikhailov 2010), we can define the ratio of the predator rate of movement to the prey rate of movement as \( \varepsilon =\frac{D_C}{D_R} \) and follow changes in abundance over time as:

$$ \frac{\mathrm{d}{R}_i}{\mathrm{d}t}=f\left({R}_i,{C}_i\right)+{D}_R{\sum}_{j=1}^n{A}_{ij}\left({R}_j-{R}_i\right) $$
(30)
$$ \frac{\mathrm{d}{C}_i}{\mathrm{d}t}=g\left({R}_i,{C}_i\right)+\varepsilon {D}_R{\sum}_{j=1}^n{A}_{ij}\left({C}_j-{C}_i\right),\mathrm{for}\ \mathrm{i}=1,\dots, n, $$
(31)

so that the rate of dispersal for the predator can be interpreted as being larger, smaller, or equal to that of the prey, depending on whether ε is larger, smaller, or equal to 1, respectively. Notice the change in notation, where the consumer population is now called C, and the resource population is now called R, to distinguish this model from that described in the previous sections, where two species competed for resources. Assuming that functions f and g do not change across sites, a consumer–resource model would typically settle to a steady state of the form \( {\overline{R}}_1={\overline{R}}_2=\dots ={\overline{R}}_n \) and \( {\overline{C}}_1={\overline{C}}_2=\dots ={\overline{C}}_n \), irrespective of dispersal rates. Let us see why this happens.

In the nonspatial scenario, i.e., there is no dispersal (DR = DC = 0), we have n independent systems of differential equations:

$$ \frac{\mathrm{d}{R}_i}{\mathrm{d}t}=f\left({R}_i,{C}_i\right) $$
(32)
$$ \frac{\mathrm{d}{C}_i}{\mathrm{d}t}=g\left({R}_i,{C}_i\right),\kern1.75em \mathrm{for}\ i=1,\dots, n, $$
(33)

which go the steady states \( {R}_1^{\ast },\dots, {R}_n^{\ast } \) and \( {C}_1^{\ast },\dots, {C}_n^{\ast } \), with \( {R}_1^{\ast }=\dots ={R}_n^{\ast } \) and \( {C}_1^{\ast }=\dots ={C}_n^{\ast } \) (to contrast between the spatial and nonspatial steady-state solutions, we use the star notation \( {R}_i^{\ast } \), \( {C}_i^{\ast } \) for the nonspatial case). When evaluated at the steady state, Eqs. (32) and (33) become \( \frac{\mathrm{d}{R}_i}{\mathrm{d}t}=f\left({R}_i^{\ast },{C}_i^{\ast}\right)=0 \) and \( \frac{\mathrm{d}{C}_i}{\mathrm{d}t}=g\left({R}_i^{\ast },{C}_i^{\ast}\right)=0 \). Then, if we evaluate the spatial model in Eqs. (30)–(31) at the steady state of the nonspatial model (32–33), we get:

$$ f\left({R}_i^{\ast },{C}_i^{\ast}\right)+D{\sum}_{j=1}^n{A}_{ij}\left({R}_j^{\ast }-{R}_i^{\ast}\right) $$
(34)
$$ g\left({R}_i^{\ast },{C}_i^{\ast}\right)+D{\sum}_{j=1}^n{A}_{ij}\left({C}_j^{\ast }-{C}_i^{\ast}\right), $$
(35)

with \( f\left({R}_i^{\ast },{C}_i^{\ast}\right)=g\left({R}_i^{\ast },{C}_i^{\ast}\right)=0 \). But because \( {R}_1^{\ast }=\dots ={R}_n^{\ast } \) and \( {C}_1^{\ast }=\dots ={C}_n^{\ast } \), then \( D{\sum}_{j=1}^n{A}_{ij}\left({R}_j^{\ast }-{R}_i^{\ast}\right)=0 \) and \( D{\sum}_{j=1}^n{A}_{ij}\left({C}_j^{\ast }-{C}_i^{\ast}\right)=0 \). Because of this, \( f\left({R}_i^{\ast },{C}_i^{\ast}\right)+D{\sum}_{j=1}^n{A}_{ij}\left({R}_j^{\ast }-{R}_i^{\ast}\right)=0 \) and \( g\left({R}_i^{\ast },{C}_i^{\ast}\right)+D{\sum}_{j=1}^n{A}_{ij}\left({C}_j^{\ast }-{C}_i^{\ast}\right)=0 \), which means \( {R}_1^{\ast }=\dots ={R}_n^{\ast } \) and \( {C}_1^{\ast }=\dots ={C}_n^{\ast } \) is also a steady-state solution of the spatial model. This result is not true whenever different steady states are expected across sites, as in the two-site competition model studied in the previous section, where the steady states for populations are mirror images of each other. In the spatial consumer–resource model presented here, \( {\overline{R}}_1={\overline{C}}_2 \) and \( {\overline{R}}_2={\overline{C}}_1 \) with \( {\overline{R}}_1\ne {\overline{R}}_2 \) and \( {\overline{C}}_1\ne {\overline{C}}_2 \).

To study the stability of such a model, and without modifying the underlying dynamics, we can again employ the Laplacian matrix notation used in Eqs. (30)–(31):

$$ \frac{\mathrm{d}{R}_i}{\mathrm{d}t}=f\left({R}_i,{C}_i\right)+{D}_R{\sum}_{j=1}^n{L}_{ij}{R}_j $$
(36)
$$ \frac{\mathrm{d}{C}_i}{\mathrm{d}t}=g\left({R}_i,{C}_i\right)+\varepsilon {D}_R{\sum}_{j=1}^n{L}_{ij}{C}_j,\kern1.5em \mathrm{for}\ i=1,\dots, n. $$
(37)

In what follows we show that the stability of the above model depends on the eigenvalues of the Jacobian matrix of the system (λi) and the eigenvalues of the Laplacian matrix of the system (Λi).

The Jacobian of the model described in Eqs. (36)–(37) is given by:

$$ \boldsymbol{J}={\left.\left(\begin{array}{ccc}\begin{array}{cc}\frac{\partial f}{\partial {R}_1}+{D}_R{L}_{11}& \frac{\partial f}{\partial {C}_1}\\ {}\frac{\partial g}{\partial {R}_1}& \frac{\partial g}{\partial {C}_1}+{\varepsilon D}_R{L}_{11}\end{array}& \cdots & \begin{array}{cc}{D}_R{L}_{1n}& 0\\ {}0& {\varepsilon D}_R{L}_{1n}\end{array}\\ {}\vdots & \ddots & \vdots \\ {}\begin{array}{cc}{D}_R{L}_{n1}& 0\\ {}0& \varepsilon {D}_R{L}_{n1}\end{array}& \cdots & \begin{array}{cc}\frac{\partial f}{\partial {R}_n}+{D}_R{L}_{nn}& \frac{\partial f}{\partial {C}_n}\\ {}\frac{\partial g}{\partial {R}_n}& \frac{\partial g}{\partial {C}_n}+{\varepsilon D}_R{L}_{nn}\end{array}\end{array}\right)\right|}_{{\overline{R}}_1,\dots, {\overline{R}}_{n,}{\overline{C}}_1,\dots, {\overline{C}}_n} $$
(38)

Assuming no dispersal (D = 0), we notice that all local Jacobians are the same when evaluated at equilibrium, because \( {\overline{R}}_1=\dots ={\overline{R}}_n \) and \( {\overline{C}}_1=\dots ={\overline{C}}_n \). Thus, (38) can be written as:

$$ \boldsymbol{J}={\boldsymbol{I}}_n\otimes {\boldsymbol{J}}_{\mathrm{nonspatial}}+\boldsymbol{L}\otimes \left(\begin{array}{cc}{D}_R& 0\\ {}0& {\varepsilon D}_R\end{array}\right)\kern0.75em , $$
(39)

where

$$ {\boldsymbol{J}}_{\mathrm{nonspatial}}={\left.\left(\begin{array}{cc}\frac{\partial f}{\partial R}& \frac{\partial f}{\partial C}\\ {}\frac{\partial g}{\partial R}& \frac{\partial g}{\partial C}\end{array}\right)\right|}_{\overline{R},\overline{C}}, $$
(40)
$$ {\boldsymbol{I}}_n=\left(\begin{array}{ccc}1& \cdots & 0\\ {}\vdots & \ddots & \vdots \\ {}0& \cdots & 1\end{array}\right), $$
(41)

and

$$ \boldsymbol{L}\otimes \left(\begin{array}{cc}{D}_R& 0\\ {}0& {\varepsilon D}_R\end{array}\right)=\left(\begin{array}{ccc}{L}_{11}& \cdots & {L}_{1n}\\ {}\vdots & \ddots & \vdots \\ {}{L}_{n1}& \cdots & {L}_{nn}\end{array}\right)\otimes \left(\begin{array}{cc}{D}_R& 0\\ {}0& {\varepsilon D}_R\end{array}\right)=\left(\begin{array}{ccc}\begin{array}{cc}{D}_R{L}_{11}& 0\\ {}0& \varepsilon {D}_R{L}_{11}\end{array}& \cdots & \begin{array}{cc}{D}_R{L}_{1n}& 0\\ {}0& \varepsilon {D}_R{L}_{1n}\end{array}\\ {}\vdots & \ddots & \vdots \\ {}\begin{array}{cc}{D}_R{L}_{n1}& 0\\ {}0& \varepsilon {D}_R{L}_{n1}\end{array}& \cdots & \begin{array}{cc}{D}_R{L}_{nn}& 0\\ {}0& {\varepsilon D}_R{L}_{nn}\end{array}\end{array}\right) $$
(42)

Because both In and L are Hermitian, we can use Friedman’s theorem (Friedman 1956), as before, and the eigenvalues of the Jacobian eigenvalues of (38) and (39) are the eigenvalues of the matrices:

$$ {\boldsymbol{J}}_{\mathrm{nonspatial}}+{\Lambda}_i\left(\begin{array}{cc}{D}_R& 0\\ {}0& {\varepsilon D}_R\end{array}\right),\kern1.25em ,i=1,\dots, n $$
(43)

or

$$ {\left.\left(\begin{array}{cc}\frac{\partial f}{\partial R}+{D}_R{\Lambda}_i& \frac{\partial f}{\partial C}\\ {}\frac{\partial g}{\partial R}& \frac{\partial g}{\partial C}+\varepsilon {D}_R{\Lambda}_i\end{array}\right)\right|}_{\overline{R},\overline{C}}\kern0.5em ,i=1,\dots, n, $$
(44)

where Λi are the eigenvalues of the Laplacian matrix, L.

If a single Jacobian eigenvalue (from the spectrum of eigenvalues given by the matrices in Eq. (44)) has positive real part, then the steady-state solution is unstable, and it is stable otherwise. If the nonspatial model is stable (DR = 0, DC = 0), but becomes unstable when dispersal is considered, it may cross a Turing bifurcation, in which the system can produce spatially inhomogeneous steady-state densities, thus giving rise to spatial pattern formation in steady-state densities. In the next section, we examine the conditions under which Turing instabilities and pattern formation may arise in a predator–prey system distributed over n sites.

Turing instability

We use Eq. (44) to assess under what conditions the model in Eqs. (37)–(38) may become spatially unstable, giving rise to spatial pattern formation in steady-state densities. For a Turing instability to arise, the nonspatial system needs to be stable; in other words, an already unstable system cannot be stabilized by dispersal. This implies that Tr(Jnonspatial) < 0 and Det(Jnonspatial) > 0. If we define \( {f}_R=\frac{\partial f}{\partial R} \), \( {f}_C=\frac{\partial f}{\partial C} \), \( {g}_R=\frac{\partial g}{\partial R} \) and \( {g}_{\mathrm{C}}=\frac{\partial g}{\partial C} \), we can write:

$$ {\boldsymbol{J}}_{\mathrm{nonspatial}}=\left(\begin{array}{cc}{f}_R& {f}_C\\ {}{g}_R& {g}_C\end{array}\right)\kern0.75em , $$
(45)

where each element of Jnonspatial depends on the partial derivatives of the functions f and g with respect to the state variables.

The stability conditions in the nonspatial system, Tr(Jnonspatial) < 0 and Det(Jnonspatial) > 0 then become:

$$ {f}_R+{g}_C<0\kern0.5em , $$
(46)
$$ {f}_R{g}_C-{f}_C{g}_R>0. $$
(47)

In contrast, the stability conditions for the spatial system are,

$$ \mathrm{Tr}\left({\boldsymbol{J}}_{\mathrm{nonspatial}}+{\Lambda}_i\left(\begin{array}{cc}{D}_R& 0\\ {}0& {\varepsilon D}_R\end{array}\right)\right)<0\kern1.5em , $$
(48)
$$ \mathrm{Det}\left({\boldsymbol{J}}_{\mathrm{nonspatial}}+{\Lambda}_i\left(\begin{array}{cc}{D}_R& 0\\ {}0& {\varepsilon D}_R\end{array}\right)\right)>0. $$
(49)

Condition (48) implies that:

$$ {f}_R+{g}_C+{\Lambda}_i\left(1+\varepsilon \right){D}_R<0\kern0.5em . $$
(50)

Because the elements of the Laplacian matrix are defined as (Lij = Aij − kiδij), its eigenvalues, Λi, must all be negative or zero (assuming that every node is connected to the spatial network). Then, using Eq. (46), it follows that:

$$ {f}_R+{g}_C+{\Lambda}_i\left(1+\varepsilon \right){D}_R\le {f}_R+{g}_C<0\kern1.25em , $$
(51)

which results in the trace of the system being always negative if the steady states of the nonspatial system are stable. For the system to be Turing unstable, the determinant of at least one of the Jacobian matrices (from Eqs. (43) and (44)) must be negative:

$$ \left({f}_R+{\Lambda}_i{D}_R\right)\left({g}_C+\varepsilon {\Lambda}_i{D}_R\right)-{f}_C{g}_R<0\kern1.5em , $$
(52)

which can be rewritten as,

$$ {f}_R{g}_C-{f}_C{g}_R+{\Lambda}_i\left({D}_R{g}_C+\varepsilon {D}_R{f}_R\right)+\varepsilon {\Lambda_i}^2{D_R}^2<0\kern0.5em . $$
(53)

Because Λi < 0, εΛi2DR2 > 0, and fRgC − fCgR > 0, we need DRgC + εDRfR > 0 for Eq. (53) to hold, which is a necessary but not sufficient condition for the emergence of a Turing instability. We observe that Eq. (53) is a concave up quadratic equation in Λi, so a sufficient condition for Eq. (53) to be negative is that it becomes negative at its minimum, which can be found by taking the derivative of Eq. (53) with respect to Λi, setting the expression to zero and solving for Λi. This results in

$$ {\Lambda_i}_{\mathrm{min}}=-\frac{D_R{g}_C+\varepsilon {D}_R{f}_R}{2\varepsilon {D_R}^2}, $$
(54)

which we can now substitute back into Eq. (53), to get

$$ {f}_R{g}_C-{f}_C{g}_R<{\frac{\left({D}_R{g}_C+\varepsilon {D}_R{f}_R\right)}{4\varepsilon {D_R}^2}}^2. $$
(55)

Using Eq. (55), we can derive, for a fixed DR, the factors that promote the onset of Turing instabilities. For example, Eq. (55) is more likely to hold for very high ε (the equation increases linearly with ε when ε is very large), or very low ε (the right-hand side expression tends to infinity as ε goes to 0). This means that Turing instabilities are more likely to occur in systems where one of the species is much more mobile than the other, as Levin’s paper also showed for a simple predator–prey system. However, whether Eq. (55) holds, and whether it is the predator or the prey mobility that matters, will ultimately depend on the specific functional forms that fR and gC take, which depend on how predator growth increases with prey density (the function f), and how prey growth is reduced by the predator (the function g). Therefore, the Turing instability in this case ultimately depends on the diagonal terms of the Jacobian matrix: \( \frac{\partial f}{\partial R}+{D}_R{\Lambda}_i \) and \( \frac{\partial g}{\partial C}+\varepsilon {D}_R{\Lambda}_i \), evaluated at steady state.

In more general terms, the ecological conditions that have been shown to promote Turing instabilities are multiple. For example, recent work has shown that Turing instabilities are likely to emerge under the influence of: 1) high nutrient supply (e.g., high prey carrying capacity); 2) weak prey intraspecific competition; 3) high prey abundance, strong intraspecific competition among predators (e.g., strong interference; Baurmann et al. 2007); 4) strongly density-dependent predator mortality term (e.g., quadratic mortality term rather than linear); and/or 5) high predator movement rates relative to prey or vice versa, as we saw in Levin’s case (Levin 1974; Baurmann et al. 2007). Interestingly, it was shown recently that in multispecies contexts, Turing bifurcations can occur for any combination of resource and consumer dispersal rates, which makes pattern formation a much more likely feature of multispecies systems than previously thought (Fanelli et al. 2013).

Finally, because Turing instabilities can arise if just one Laplacian eigenvalue Λi (Eq. 54) satisfies Eq. (55), and given that the Laplacian matrix is determined by the structure of the underlying spatial network, it follows that the spatial movement of individuals can have an important effect on whether the Turing bifurcation occurs for a given set of interactions and rate laws. In what follows we explore numerically some of these results and discuss some potential ecological consequences of crossing the Turing bifurcation.

Complex underlying spatial networks and the ecological consequences of Turing instabilities

In this section, we explore the ecological consequences of the onset of Turing instabilities. To do so, we focus on two consumer–resource models, a modified Rosenzweig–MacArthur (RMA) model that considers density-dependent predator mortality (the classic RMA model considers density-independent per capita mortality for the predator, but strong density dependence is needed for Turing instabilities to be present) and a modified Mimura–Murray (MM) model that considers a type-I functional response and strongly density-dependent mortality for the predator. This latter model has been shown before to exhibit pattern formation as well (Nakao and Mikhailov 2010), which is why we adopt it in this paper. The RMA model determines the population density of predators (C) and prey (R) over time, where r is the maximum per capita growth rate of the prey; K is its carrying capacity; α and η are the attack rate and handling time of the predator, respectively; e is the conversion efficiency of the predator; and d is its per capita death rate. As before, we assume that individuals can move across patches at a rate DR for the prey and εDR for the predator. Taken together, the abundances of n populations of the predator and prey change over time as

$$ \frac{\mathrm{d}{R}_i}{\mathrm{d}t}=r{R}_i\left(1-\frac{R_i}{K}\right)-\frac{\alpha {R}_i{C}_i}{1+\alpha \eta {R}_i}+{D}_R{\sum}_{j=1}^n{L}_{ij}{R}_j $$
(56)
$$ \frac{\mathrm{d}{C}_i}{\mathrm{d}t}=e\frac{\alpha {R}_i{C}_i}{1+\alpha \eta {R}_i}-\mathrm{d}{C_i}^2+\varepsilon {D}_R{\sum}_{j=1}^n{L}_{ij}{C}_j,\kern1.5em \mathrm{for}\ i=1,\dots, n, $$
(57)

which shares similarities with the model of a previous study (Turchin and Batzli 2001). In a similar vein, the MM model incorporates two additional parameters A and B (Mimura and Murray 1978) that control the strength of the (weak) Allee effect (where all other parameters are as before), with dynamics determined by

$$ \frac{\mathrm{d}{R}_i}{\mathrm{d}t}=r{R}_i\left(1-\frac{R_i}{K}\right)\left(\frac{R_i}{A}+B\right)-{R}_i{C}_i+{D}_R{\sum}_{j=1}^n{L}_{ij}{R}_j $$
(58)
$$ \frac{\mathrm{d}{C}_i}{\mathrm{d}t}={R}_i{C}_i-\left(1+\mathrm{d}{C}_i\right){C}_i+\varepsilon {D}_R{\sum}_{j=1}^n{L}_{ij}{C}_j,\kern1.75em \mathrm{for}\ i=1,\dots, n. $$
(59)

First, we illustrate the onset of Turing instabilities by assessing the effect of predator dispersal on the Jacobian determinants and the signs of their eigenvalues. We observe that, as stated before, an increase in the predator movement rate, ε, leads to negative determinants (Fig. 4a, c) and positive Jacobian eigenvalues in both models (Fig. 4b, d), hence Turing instability. As we have shown, the stability of the steady states of the model are determined by the eigenvalues of the Laplacian matrix associated to the underlying spatial network, emphasizing the importance of spatial patterns of dispersal for determining ecological dynamics.

Fig. 4
figure 4

a Determinant versus trace of the Jacobian matrix of the Rosenzweig–MacArthur model for an underlying spatial network with 100 patches and for increasing predator migration rates (ε = 1, in blue, to ε = 50, in red). Gray (ε = 2), dark gray (ε = 25), and black (ε = 50) dashed lines represent the relationship between the two variables and its change with ε, for visualization purposes. The first instance where the determinant becomes negative (onset of the Turing bifurcation) is marked with a black arrow. b Real part of the maximum eigenvalue for all Jacobian matrices or the RMA model against the predator movement rate ε. Colors for visualization purposes only indicate the different modes (each one associated with a site). The onset of the Turing bifurcation also indicated as a black arrow. c Same as in a but for the MM model. d Same as in b but for the MM model. We can see in all cases how an increase in ε leads to a Turing bifurcation. RMA model parameters: r= 4, K= 7.533, d= 1.8, e= 0.4, α= 9.533, η= 0.105. MM model parameters (from Nakao and Mikhailov 2010): A = 0.0557, B= 35, K= 17.95, d= 0.4, r = 1/9

Full size image

Crossing the Turing bifurcation leads to spatially inhomogeneous steady-state densities for the MM model, where the populations occupying each site go to steady-state densities similar to those attained in the nonspatial case in some sites, but alternative steady-state densities in other sites (Fig. 5). A previous study has shown that prey dispersal rate controls where in the spatial network these alternative steady states appear as a result of the Turing instability (Nakao and Mikhailov 2010). If the prey dispersal rate is low, the alternative steady states appear in patches that are more interconnected (i.e., nodes with high degree or hubs, Fig. 5a, b), whereas when the prey dispersal rate is high, the alternative steady states appear in patches with fewer connections (i.e., peripheral nodes) (Fig. 5c, d).

Fig. 5
figure 5

a Time series for the MM model (ε = 18, DR = 0.06) showing the onset of the Turing bifurcation and how it leads to different steady-state densities for both predators (purple) and prey (orange). b 100-site underlying species network where the dynamics in a occur, showing how, for low prey movement rate (DR = 0.06), the steady-state densities that differ from the nonspatial values occur in the hubs of the network (red = high density, blue = low density, yellow = density comparable to nonspatial steady-state density). c As in a but for larger prey movement rate (DR = 0.45). d As in b but for DR = 0.45, showing how for larger prey movement rates, the alternative steady-state solutions occur in peripheral nodes (same color code as in b). Parameter values as in Fig. 4

Full size image

Given how potentially pervasive Turing instabilities can be, what are the effects of these dynamics on species persistence? The classic perception in ecology is that unstable steady-state solutions lead to larger extinction risk and, thus, lower persistence (e.g., May 1972; McCann 2000; Rooney and McCann 2011; Allesina and Tang 2012); however, the potential for systems to exhibit spatial pattern formation via Turing instabilities suggests that this perception may be more nuanced (Earn 2000). To address this question, we assessed how persistence in the metapopulation was affected by Turing instability as a function of spatial connectivity. To do so, we numerically solved the MM model for 1000 time steps across increasingly interconnected (high average node degree) spatial networks. For each parameter set, we numerically solved the model 100 times and evaluated numerically whether the system showed spatial pattern formation or not. Our results suggest that the region over which the Turing instability arises depends on the average node degree of the network, with more interconnected underlying spatial networks being less prone to exhibit Turing instabilities (Fig. 6a).

Fig. 6
figure 6

a Frequency of Turing unstable dynamics for all combinations of the average node degree and predator movement rate and 50 site underlying spatial networks. Each combination of parameters was run 100 times. b Same as in a but the number of local extinctions is quantified. c Same as in a and b, but where the portfolio of the whole metapopulation was quantified, where a portfolio equal to 1 suggests larger global extinction probability and a larger portfolio suggests a lower global extinction probability. All the other parameters as in Fig. 4

Full size image

It is widely assumed that instability leads to higher extinction risk in predator–prey systems (McCann 2000), largely because instability in nonspatial models results in widely fluctuating populations that spend much time near their extinction thresholds, thus increasing the chance of stochastic extinctions. To assess under what conditions instability led to fluctuations and extinction, we used two different proxies of extinction risk: the number of local extinctions and the portfolio effect of the metapopulation, i.e., to what extent the aggregate metapopulation dampens local fluctuations in population densities. The latter metric is frequently used to evaluate robustness in natural populations (Schindler et al. 2010; Anderson et al. 2015; Moore et al. 2015). To calculate the number of stochastic extinctions, we used a stochastic differential equation version of the model in Eqs. (58)–(59) that considers low levels of additive demographic stochasticity (i.e., Weiner process without drift and standard deviation equal to 1). An extinction event was assumed to occur whenever a local population density fell below 10−4. To evaluate robustness to fluctuations, we calculated the average portfolio effect (PE) for the metapopulation (Anderson et al. 2015; Schindler et al. 2015) after transients have subsided using the same stochastic model. The PE is calculated as the average coefficient of variation (CV) in population abundance across each population, divided by the CV of the aggregate:

$$ \mathrm{PE}=\frac{\left\langle {\mathrm{CV}}_{\mathrm{ind}}\right\rangle }{{\mathrm{CV}}_{\mathrm{tot}}}, $$
(60)

where 〈CVind〉 is the standard deviation of the abundance of each population individually, divided by their mean abundance at equilibrium, averaged across all sites, and CVtot is the same but for the sum of abundances across all populations. As CVtot decreases relative to that of the constituent populations, PE > 1, and the metapopulation becomes more robust by dampening the fluctuations of its constituent populations. Portfolio effects greater than unity typically are associated with lower levels of synchronization (Loreau and de Mazancourt 2008; Anderson et al. 2015), increasing the potential for demographic rescue between populations, thus buffering the metapopulation against extinction.

In our spatial model, the Turing instability leads to a greater chance of local extinction with larger ε (measured as the number of local patches that at any point in time fall below 10−4, Fig. 6b), but larger portfolio effects (Fig. 6c), suggesting that although the risk of local extinction is higher, the overall robustness of the metapopulation may be enhanced. Moreover, there is a sizeable region of parameter space where the Turing bifurcation has been crossed, the portfolio effect is large, and where the probability of local extinctions is low. The existence of this region suggests that there is an intermediate dispersal rate that promotes persistence both by minimizing local extinctions and by increasing the capacity of the metapopulations to buffer against variation in individual population densities. Thus, with the onset of the Turing instability, even though local extinction spikes, rescue effects are strong, which increases overall persistence. These results suggest that instability may facilitate—rather than limit—the persistence of predator–prey systems, and this more nuanced perspective is particularly relevant when comparing local extinctions, which are likely temporary, to the persistence of the larger metapopulation.

Whereas Levin’s results showed the importance of spatially induced instabilities for pattern formation, we have shown that these same instabilities can lead to higher portfolio effects, which increases the potential for ecological rescue, thereby offsetting the spike in local extinction risk associated with increased dispersal rates. Importantly, both Levin’s original work and our results stress the importance of spatial instabilities in shaping species persistence and perhaps buffering metapopulations against extinction.

Final thoughts

Revisiting Levin (1974), we have reviewed and expanded upon the original message: space and spatial processes have paramount consequences for the persistence and dynamics of interacting populations. The spatial structure and dispersal of species can promote the coexistence of competing species and can lead to spatial pattern formation, which in turn may increase species persistence. In this paper, we have explored some of the broader consequences of Levin’s message, while placing these classic results in the context of recent advances, revealing the importance and utility of the Laplacian matrix as a way to assess ecological dynamics without necessarily knowing in advance the regulatory processes controlling inter- and intraspecific interactions. Together, these results highlight the importance of taking spatial structure into account, especially in a context of future ecosystems, where an increasingly fragmented landscape will require the incorporation of spatial constraints into our understanding of ecological relationships. Space, both the constraints it imposes and the freedom it allows, elevates the dynamical richness that we observe in ecological systems and, as we have seen, can both facilitate and limit persistence, depending on its structure. As our understanding of the role of space and spatial processes continues to develop, it is opportune to recall the continued impact of the framework introduced by Levin in 1974 on contemporary theoretical approaches, and in what directions our ideas and methods have since dispersed.