A fair and efficient resource sharing scheme using modified grey wolf optimizer

Abstract

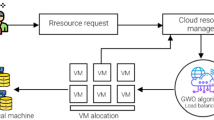
With the rapid upsurge in large-scale computing, resource sharing in heterogeneous distributed systems where users’ goals are conflicting has become a paramount research issue. The resource sharing or resource allocation problem is attributed to allocating users’ tasks across multiple computing resources so that the utility of the resources is improved while ensuring the quality of services. In this paper, the resource allocation problem is considered as a bi-objective optimization problem, including minimizing response time and the utilization imbalance between resources. To optimize both the objectives simultaneously, the contributions of this paper are manifolds. First, the problem is modeled as an optimization problem by considering both the objectives in an integrated manner. Second, the resource allocation problem is formulated as a non-cooperative game. Finally, to derive the game’s solution in a distributed manner, a Best Response dynamics based Modified Grey Wolf Optimizer BR-MGWO is proposed. Further, to assess the efficacy of BR-MGWO, it is compared with two other approaches, i.e., GOS and NCOP on problem instances of various settings. The experimental results show that BR-MGWO not only provides less response time while provides better improvements in utilization imbalance, which is reduced by 50% and 71%, respectively, in comparison to the GOS and NCOP.

Appendices

Appendix A Performance Analysis of MGWO

This appendix section presents the rationale behind the development of MGWO, i.e., the performance analysis of MGWO with respect to its canonical version—GWO.

Since our purpose (following the scope of this paper) is to justify the reasoning of introducing MGWO instead of not adopting GWO. In this regard, we consider four benchmarks functions [28] to divulge the performance of MGWO and GWO. This suite of benchmark that is also utilized in various prior studies [27, 28, 33, 34], has two types of functions: (a) unimodal and (b) multimodel. The surface plots of the functions are shown in Fig. 10 and their mathematical representation, along with their properties, are discussed below. Note that all the functions considered are minimization functions, with the global minimum for all the functions is 0.

1.1 Unimodal functions

A function is called unimodal if it has only one local optimum (referred to as global optimum). A unimodal function is used to test the exploitation capability (i.e., the algorithm’s convergence rate). In this experiment, we have considered two unimodal functions:

• Sphere function it is considered as the simplest optimization function to solve. The surface plot for this function is shown in Fig. 10a. The search range for this function is selected [− 100,100]. Mathematically, it is defined as:

  $$\begin{aligned} F_1 ({\mathbf {x}}) = \sum _{i=1}^{d} x_i^2, \end{aligned}$$

  (18)

  where ${\mathbf {x}} = (x_i)_{i=1}^d$ is a d-dimensional vector.

• Schwefel function as shown in Fig. 10b, this function has sharp corners of the contours, which increase the chances of getting stuck for an algorithm. So, it is considered as one of the challenging problems to solve. The search range for this function is selected [− 10,10]. Mathematically, it is defined as:

  $$\begin{aligned} F_2 ({\mathbf {x}}) = \sum _{i=1}^{d} |x_i| + \prod _{i=1}^{d} |x_i|. \end{aligned}$$

  (19)

1.1.1 Multimodal functions

A function is called multimodal if it has more than one local optimum other than the global optimum. A multimodal function is used to test the exploration capability (i.e., the capability of escaping from local optima trapping) of the algorithm. Here, we have considered two multimodal functions:

• Ackley function as shown in Fig. 10c, this function contains many local optima, and the global optimum lies in the narrow basin. The search range for this function is [− 32, 32]. Mathematically, it is defined as:

  $$\begin{aligned} F_3 ({\mathbf {x}})= & {} -20*e^{\Big (-0.2 \sqrt{\frac{1}{d}\sum _{i=1}^{d}x_i^2}\Big )} - e^{\Big (\frac{1}{d}\sum _{i=1}^{d}cos(2\pi x_i)\Big )}\nonumber \\&+ 20 +e . \end{aligned}$$

  (20)

• Griewank function as shown in Fig. 10d, this function is a complex function, having regularly distributed many local optima. There are high chances for an algorithm to get stuck in local optimum. The search range for this function is selected [− 5.12,5.12]. Mathematically, it is defined as:

  $$\begin{aligned} F_4 ({\mathbf {x}}) = \sum _{i=1}^{d} (x_i^2 - 10cos(2\pi x_i) +10). \end{aligned}$$

  (21)

Fig. 10

Surface plot for benchmark functions

1.2 Parameter settings

The parameters used for experiments are as follows. For each function, dimension size and population size are fixed to 30 [27, 28]. The value of $p_r = 0.5$. The stopping criteria for MGWO and GWO are the maximum number of iterations that is set to 500. For each experiment, 30 independent runs are performed, and final results are reported after averaging 30 runs.

Fig. 11

Illustrating the convergence behavior

1.3 Experimental results and discussion

In this set of experiments, to gauge the goodness of MGWO and GWO, two evaluation metrics, i.e., convergence rate and the average optimal value is adopted. The convergence rate of an optimization algorithm is defined as the speed at which the algorithm approaches the objective function’s optimal value. Here, optimal value means what is the objection function value after the final iteration of the algorithm.

The convergence behavior of MGWO and GWO for four different benchmark functions are shown in Fig. 11. From Fig. 11a, b, it can be observed that in early stage of the optimization process the convergence rate of GWO better than MGWO, and as iteration increases MGWO outperforms GWO. Finally, the optimal value achieved by MGWO, i.e., 1.73e−253, is much better than the value, i.e., 5.17e−28, achieved by GWO.

From Fig. 11c, d, it can be seen that in both the multimodal functions GWO gets trapped into local optima and converges prematurely while MGWO with its better exploration capability achieves a better value without getting trapped in early iterations. The optimal value achieved by MGWO for $F_3$ and $F_4$ is 0 and 8.86e−16, respectively.

Finally, from empirical results, it can be inferred that MGWO outperforms GWO in terms of exploration and exploitation capability. This better performance of MGWO over GWO motivates and led us to use MGWO for finding NE in combination with best response dynamics.

1.4 Parameter sensitivity analysis

In our proposed MGWO, we have used only one additional parameter, i.e., $p_r$ other than GWO. To perform all the experiments, we have fixed the value of $p_r = 0.5$. The reason for fixing this value is established experimentally in this section.

In order to analyze the sensitivity of $p_r$ over the performance of MGWO, we considered one unimodal function and one multimodal function. All other parameters used in this experiment are considered the same as in the previous experiment. The final objective value function achieved over varying range of $p_r$ (i.e., from 0.1 to 0.9) are reported in the Table 8. From the results shown in the second column of the Table 8, it can be seen that:

Table 8 Objective functions values over varying $p_r$

• for unimodal function when the value of $p_r$ is less than 0.5, the objective function value is better, and on the other hand, as value of $p_r$ increases beyond 0.5, the performance of the MGWO deteriorates.

• for multimodal function when the value of $p_r$ decreases beyond 0.5, the performance of the MGWO deteriorates, and on the other hand, the performance remains consistent if the value of $p_r$ is 0.5 or beyond.

From these results, it is clear that the value of $p_r$ less than 0.5 is better for unimodal but affects the algorithm’s performance severely in the case of multimodal. Therefore, the best-suited value of $p_r$ is 0.5.

Appendix B Wilcoxon signed-rank test

The Wilcoxon signed-rank test [31, 32] is a pairwise test that is designed to investigate the significant difference between two sample means; it is nonparametric procedure and is analogous to paired t-test. If these samples are refer to the output of two different algorithms, then this test is used for answering the following question: does there exist any significant difference between the performance of the two algorithms?

Let there are Q different output points of the algorithms on different function (or different configuration settings), and $\delta _i$ be the performance difference of the two algorithms on i th output point. Let $rk^+$ be the sum of ranks for the output points where first algorithm outperforms second, and $rk^-$ is the sum of ranks for opposite outcome. Ranks of $\delta _i =0$ are split evenly among the sums [31]; if there is an odd number of them, then one is ignored:

$$\begin{aligned} \begin{aligned} rk^+&= \sum _{\delta _i >0} rank(\delta _i) + \frac{1}{2}\sum _{\delta _i = 0} rank(\delta _i)\\ rk^-&= \sum _{\delta _i < 0} rank(\delta _i) + \frac{1}{2}\sum _{\delta _i = 0} rank(\delta _i) \end{aligned} \end{aligned}$$

(22)

Let ${\mathbb {T}} = \min (rk+, rk_)$ be the smaller of the ranks sums. If ${\mathbb {T}}$ is less than or equal to the value of the distribution of Wilcoxon for Q degrees of freedom ([35] Table B.12), then the null hypothesis of equality of performance is rejected; this means that the performance of the given algorithm is better than the other one, with the p value associated.