Skip to main content

Advertisement

SpringerLink
Log in

Understanding industrial energy productivity growth in China: a production-theoretical approach

  • Original Article
  • Published:
Energy Efficiency Aims and scope Submit manuscript

Abstract

The purpose of this paper is to investigate the driving force behind industrial energy productivity growth in China from 2005 to 2010. The model of Wang (Energy, 32(8), 1326–1333, 2007) is extended to accommodate different technologies by relaxing the constant return to scale (CRS) assumption. In the empirical study, we find that (1) technological changes and capital-energy substitution are the main contributors to the increase in industrial energy productivity; (2) impacts of changes in technical efficiency, energy composition, and output structure are relatively trivial; (3) the effect of labor-energy substitution is unfavorable to industrial energy productivity growth.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. The numerical values are calculated by the author according to the data from China Statistical Yearbook.

  2. According to China Statistical Yearbook, China’s industrial energy productivity declined from 5.5 thousand RMB/TCE in 2000 to 4.9 thousand RMB/TCE in 2005 (2005 price).

  3. For example, Liu et al. (2011) found that 17 selected sectors in manufacturing industry in China did not show CRS technology. Wang (2007) also pointed out that the hypothesis of CRS technology was rejected in many empirical works.

  4. We thank an anonymous reviewer for pointing out this.

  5. Ang (2004) provided a useful summary and comparison of the various methods.

  6. We thank an anonymous reviewer for pointing out this.

  7. Zhou and Ang (2008a) also provided a brief comparison between SDA, IDA and PDA.

  8. We follow Wang (2007) to decompose energy productivity change based on the distance function. We also notice that a recent study, Wang et al. (2013) conducted the decomposition of total energy productivity in the context of directional distance function (DDF). It is a nice idea since DDF can take into account undesirable outputs. However, the energy productivity defined in our paper belongs to PFEE indicators, different from that in Wang et al. (2013). The decomposition based on the DDF is not applicable in our case.

  9. Under CRS technology, the output distance function is homogeneous degree of −1 in inputs.

  10. One can choose a specific type of technology based on the judgment of the real technologies to apply the model.

  11. Due to the unavailability of the data, Tibet is not considered in this study.

  12. The heavy and light industries are classified according to the criteria of Chinese National Bureau of Statistics which can be found in Appendix 3.

  13. The gross output measure has the double counting problem. Hence, the gross output data should not be directly used.

  14. They are provided by China Industrial Economy Statistical Yearbook. Enterprises above designated size are defined by enterprises of which total annual turnover exceed 5 million RMB.

  15. Due to data limitation, we only have observations in 2005 and 2010. Thus, in our empirical studies, we actually use observations in 2005 to construct the frontier for 2005 and use observations both in 2005 and 2010 to construct the frontier for 2010. But, this is essentially in line with the sequential DEA method.

  16. In practice, the LPs for cross-period distance function (specially when the technology in previous year is used to estimate the distance function in a later year) may become infeasible which would challenge the empirical analysis. We thank an anonymous reviewer for pointing out this issue. We discuss this in Appendix 4. But note that our empirical study does not encounter infeasibility.

References

  • Alcantara, V., & Duarte, R. (2004). Comparison of energy intensities in European Union countries. Results of a structural decomposition analysis. Energy Policy, 32(2), 177–189.

    Article  Google Scholar 

  • Ang, B. (2004). Decomposition analysis for policymaking in energy: which is the preferred method? Energy Policy, 32(9), 1131–1139.

    Article  Google Scholar 

  • Ang, B., Mu, A., & Zhou, P. (2010). Accounting frameworks for tracking energy efficiency trends. Energy Economics, 32(5), 1209–1219.

    Article  Google Scholar 

  • Chang, T.-P., & Hu, J.-L. (2010). Total-factor energy productivity growth, technical progress, and efficiency change: an empirical study of China. Applied Energy, 87(10), 3262–3270.

    Article  Google Scholar 

  • China Economic Census Yearbook (CECY). China Statistics Press, Beijing; 2004, 2008. [In Chinese].

  • China Energy Statistical Yearbook (CESY). China Statistics Press, Beijing; 2006–2010. [In Chinese].

  • China Industrial Economy Statistical Yearbook (CIESY). China Statistics Press, Beijing; 2006–2010. [In Chinese].

  • China Statistical Yearbook (CSY). China Statistics Press, Beijing; (2001, 2006, 2012). [in Chinese].

  • Choi, K.-H., & Ang, B. (2012). Attribution of changes in Divisia real energy intensity index—an extension to index decomposition analysis. Energy Economics, 34(1), 171–176.

    Article  Google Scholar 

  • Färe, R., Grosskopf, S., Norris, M., & Zhang, Z. (1994). Productivity growth, technical progress, and efficiency change in industrialized countries. The American economic review, 66–83.

  • Garbaccio, R., Ho, M. S., & Jorgenson, D. W. (1999). Why has the energy-output ratio fallen in China? Energy J, 20, 63–92.

    Article  Google Scholar 

  • Hankinson, G. A., & Rhys, J. (1983). Electricity consumption, electricity intensity and industrial structure. Energy Economics, 5(3), 146–152.

    Article  Google Scholar 

  • Hoekstra, R., & Van den Bergh, J. C. (2003). Comparing structural decomposition analysis and index. Energy Economics, 25(1), 39–64.

    Article  Google Scholar 

  • Hu, J.-L., & Wang, S.-C. (2006). Total-factor energy efficiency of regions in China. Energy Policy, 34(17), 3206–3217.

    Article  Google Scholar 

  • Huang, J.-p. (1993). Industry energy use and structural change: a case study of the People’s Republic of China. Energy Economics, 15(2), 131–136.

    Article  Google Scholar 

  • Kagawa, S., & Inamura, H. (2001). A structural decomposition of energy consumption based on a hybrid rectangular input-output framework: Japan’s case. Economic Systems Research, 13(4), 339–363.

    Article  Google Scholar 

  • Kim, K., & Kim, Y. (2012). International comparison of industrial CO2 emission trends and the energy efficiency paradox utilizing production-based decomposition. Energy Economics, 34(5), 1724–1741.

    Article  Google Scholar 

  • Lee, C.-C. (2005). Energy consumption and GDP in developing countries: a cointegrated panel analysis. Energy Economics, 27(3), 415–427.

    Article  Google Scholar 

  • Lin, X., & Polenske, K. R. (1995). Input–output anatomy of China’s energy use changes in the 1980s. Economic Systems Research, 7(1), 67–84.

    Article  Google Scholar 

  • Liu, A., Gao, G., & Yang, K. (2011). Returns to scale in the production of selected manufacturing sectors in China. Energy Procedia, 5, 604–612.

    Article  Google Scholar 

  • Ma, C., & Stern, D. I. (2008). China’s changing energy intensity trend: a decomposition analysis. Energy Economics, 30(3), 1037–1053.

    Article  Google Scholar 

  • Oh, D.-h., & Heshmati, A. (2010). A sequential Malmquist–Luenberger productivity index: environmentally sensitive productivity growth considering the progressive nature of technology. Energy Economics, 32(6), 1345–1355.

    Article  Google Scholar 

  • Pastor, J. T., & Lovell, C. (2005). A global Malmquist productivity index. Economics Letters, 88(2), 266–271.

  • Pasurka, C. A., Jr. (2006). Decomposing electric power plant emissions within a joint production framework. Energy Economics, 28(1), 26–43.

    Article  Google Scholar 

  • Shi, X., & Polenske, K. R. (2006). Energy prices and energy intensity in China: a structural decomposition analysis and econometrics study. MIT Center for Energy and Environmental Policy Research, Working Paper.

  • Shi, G.-M., Bi, J., & Wang, J.-N. (2010). Chinese regional industrial energy efficiency evaluation based on a DEA model of fixing non-energy inputs. Energy Policy, 38(10), 6172–6179.

    Article  Google Scholar 

  • Sinton, J. E., & Levine, M. D. (1994). Changing energy intensity in Chinese industry: the relatively importance of structural shift and intensity change. Energy Policy, 22(3), 239–255.

    Article  Google Scholar 

  • Song, F., & Zheng, X. (2012). What drives the change in China’s energy intensity: combining decomposition analysis and econometric analysis at the provincial level. Energy Policy.

  • Soytas, U., & Sari, R. (2009). Energy consumption, economic growth, and carbon emissions: challenges faced by an EU candidate member. Ecological Economics, 68(6), 1667–1675.

    Article  Google Scholar 

  • Tulkens, H., & Vanden Eeckaut, P. (1995). Non-parametric efficiency, progress and regress measures for panel data: methodological aspects. Eur J Oper Res, 80(3), 474–499.

    Article  MATH  Google Scholar 

  • Wang, C. (2007). Decomposing energy productivity change: a distance function approach. Energy, 32(8), 1326–1333.

    Article  Google Scholar 

  • Wang, C. (2011). Sources of energy productivity growth and its distribution dynamics in China. Resource and Energy Economics, 33(1), 279–292.

    Article  Google Scholar 

  • Wang, C. (2013). Changing energy intensity of economies in the world and its decomposition. Energy Economics, 40, 637–644.

    Article  Google Scholar 

  • Wang, H., Zhou, P., & Zhou, D. (2013). Scenario-based energy efficiency and productivity in China: a non-radial directional distance function analysis. Energy Economics, 40, 795–803.

    Article  Google Scholar 

  • Wei, C., Ni, J., & Shen, M. (2009). Empirical analysis of provincial energy efficiency in China. China World Econ, 17(5), 88–103.

    Article  Google Scholar 

  • Wilson, P. W. (2008). FEAR: a software package for frontier efficiency analysis with R. Socio-Economic Planning Sciences, 42(4), 247–254.

    Article  Google Scholar 

  • Wu, Y. (2012). Energy intensity and its determinants in China’s regional economies. Energy Policy, 41, 703–711.

    Article  Google Scholar 

  • Wu, F., Fan, L., Zhou, P., & Zhou, D. (2012). Industrial energy efficiency with CO2 emissions in China: a nonparametric analysis. Energy Policy, 49, 164–172.

  • Xia, Y., Yang, C., & Chen, X. (2012). Structural decomposition analysis on China’s energy intensity change for 1987–2005. Journal of Systems Science and Complexity, 25(1), 156–166.

    Article  MATH  Google Scholar 

  • Zaim, O. (2004). Measuring environmental performance of state manufacturing through changes in pollution intensities: a DEA framework. Ecological Economics, 48(1), 37–47.

    Article  Google Scholar 

  • Zhang, Z. (2003). Why did the energy intensity fall in China’s industrial sector in the 1990s? The relative importance of structural change and intensity change. Energy Economics, 25(6), 625–638.

    Article  Google Scholar 

  • Zhang, N., & Choi, Y. (2013). Total-factor carbon emission performance of fossil fuel power plants in China: a metafrontier non-radial Malmquist index analysis. Energy Economics, 40, 549–559. doi:10.1016/j.eneco.2013.08.012.

    Article  Google Scholar 

  • Zhang, X.-P., Zhang, J., & Tan, Q.-L. (2013). Decomposing the change of CO2 emissions: a joint production theoretical approach. Energy Policy, 58, 329–336. doi:10.1016/j.enpol.2013.03.034.

    Article  Google Scholar 

  • Zhou, P., & Ang, B. (2008a). Decomposition of aggregate CO2 emissions: a production-theoretical approach. Energy Economics, 30(3), 1054–1067.

    Article  Google Scholar 

  • Zhou, P., & Ang, B. (2008b). Linear programming models for measuring economy-wide energy efficiency performance. Energy Policy, 36(8), 2911–2916.

    Article  Google Scholar 

  • Zhou, P., Ang, B., & Poh, K. (2008). Measuring environmental performance under different environmental DEA technologies. Energy Economics, 30(1), 1–14.

    Article  MathSciNet  Google Scholar 

  • Zhou, P., Ang, B., & Zhou, D. (2012). Measuring economy-wide energy efficiency performance: a parametric frontier approach. Applied Energy, 90(1), 196–200.

    Article  Google Scholar 

Download references

Acknowledgments

We thank three anonymous reviewers for their helpful comments and suggestion which led to an improved version of this paper. Financial support from Yinxing Economic Research Fund is gratefully acknowledged.

Author information

Authors and Affiliations

  1. School of Energy Research, Xiamen University, Xiamen, 361005, China

    Kerui Du

  2. Department of Agricultural and Resource Economics, University of Connecticut, Storrs, CT, 06269-4021, USA

    Lu Huang

  3. Guanghua School of Management, Peking University , Beijing, 100037, China

    Zhiming Yang

Authors
  1. Kerui Du
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lu Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhiming Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kerui Du.

Additional information

Highlights

• The original PDA model is extended to accommodate different technologies.

• Technological progress is the main driver of industrial energy productivity growth.

• Capital-energy substitution contributes to industrial energy productivity growth.

Appendices

Appendix 1

The whole decomposition of Eq. (7):

$$ \begin{array}{l}\frac{D_t^c\left({l}_t,{k}_t,{e}_t,{y}_t\right)}{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_{\tau },{y}_{\tau}\right)}\hfill \\ {}={\left[\begin{array}{c}\hfill {\left(\frac{D_t^c\left({l}_t,{k}_t,{e}_t,{y}_t\right)}{D_t^c\left({l}_{\tau },{k}_t,{e}_t,{y}_t\right)}\right)}^6\times {\left(\frac{D_t^c\left({l}_t,{k}_{\tau },{e}_{\tau },{y}_{\tau}\right)}{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_{\tau },{y}_{\tau}\right)}\right)}^6\hfill \\ {}\hfill \times {\left(\frac{D_t^c\left({l}_t,{k}_{\tau },{e}_{\tau },{y}_t\right)}{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_{\tau },{y}_t\right)}\right)}^2\times {\left(\frac{D_t^c\left({l}_t,{k}_{\tau },{e}_t,{y}_{\tau}\right)}{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_t,{y}_{\tau}\right)}\right)}^2\hfill \\ {}\hfill \times {\left(\frac{D_t^c\left({l}_t,{k}_t,{e}_{\tau },{y}_{\tau}\right)}{D_t^c\left({l}_{\tau },{k}_t,{e}_{\tau },{y}_{\tau}\right)}\right)}^2\times {\left(\frac{D_t^c\left({l}_t,{k}_{\tau },{e}_t,{y}_t\right)}{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_t,{y}_t\right)}\right)}^2\hfill \\ {}\hfill \times {\left(\frac{D_t^c\left({l}_t,{k}_t,{e}_{\tau },{y}_t\right)}{D_t^c\left({l}_{\tau },{k}_t,{e}_{\tau },{y}_t\right)}\right)}^2\times {\left(\frac{D_t^c\left({l}_t,{k}_t,{e}_t,{y}_{\tau}\right)}{D_t^c\left({l}_{\tau },{k}_t,{e}_t,{y}_{\tau}\right)}\right)}^2\hfill \end{array}\right]}^{1/24}\hfill \\ {}\times {\left[\begin{array}{l}{\left(\frac{D_t^c\left({l}_t,{k}_t,{e}_t,{y}_t\right)}{D_t^c\left({l}_t,{k}_{\tau },{e}_t,{y}_t\right)}\right)}^6\times {\left(\frac{D_t^c\left({l}_{\tau },{k}_t,{e}_{\tau },{y}_{\tau}\right)}{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_{\tau },{y}_{\tau}\right)}\right)}^6\hfill \\ {}\times {\left(\frac{D_t^c\left({l}_{\tau },{k}_t,{e}_{\tau },{y}_t\right)}{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_{\tau },{y}_t\right)}\right)}^2\times {\left(\frac{D_t^c\left({l}_{\tau },{k}_t,{e}_t,{y}_{\tau}\right)}{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_t,{y}_{\tau}\right)}\right)}^2\hfill \\ {}\times {\left(\frac{D_t^c\left({l}_t,{k}_t,{e}_{\tau },{y}_{\tau}\right)}{D_t^c\left({l}_t,{k}_{\tau },{e}_{\tau },{y}_{\tau}\right)}\right)}^2\times {\left(\frac{D_t^c\left({l}_{\tau },{k}_t,{e}_t,{y}_t\right)}{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_t,{y}_t\right)}\right)}^2\hfill \\ {}\times {\left(\frac{D_t^c\left({l}_t,{k}_t,{e}_{\tau },{y}_{\tau}\right)}{D_t^c\left({l}_t,{k}_{\tau },{e}_{\tau },{y}_t\right)}\right)}^2\times {\left(\frac{D_t^c\left({l}_t,{k}_t,{e}_t,{y}_{\tau}\right)}{D_t^c\left({l}_t,{k}_{\tau },{e}_t,{y}_{\tau}\right)}\right)}^2\hfill \end{array}\right]}^{1/24}\hfill \\ {}\times {\left[\begin{array}{l}{\left(\frac{D_t^c\left({l}_t,{k}_t,{e}_t,{y}_t\right)}{D_t^c\left({l}_t,{k}_t,{e}_{\tau },{y}_t\right)}\right)}^6\times {\left(\frac{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_t,{y}_{\tau}\right)}{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_{\tau },{y}_{\tau}\right)}\right)}^6\hfill \\ {}\times {\left(\frac{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_t,{y}_t\right)}{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_{\tau },{y}_t\right)}\right)}^2\times {\left(\frac{D_t^c\left({l}_t,{k}_{\tau },{e}_t,{y}_{\tau}\right)}{D_t^c\left({l}_t,{k}_{\tau },{e}_{\tau },{y}_{\tau}\right)}\right)}^2\hfill \\ {}\times {\left(\frac{D_t^c\left({l}_{\tau },{k}_t,{e}_t,{y}_{\tau}\right)}{D_t^c\left({l}_{\tau },{k}_t,{e}_{\tau },{y}_{\tau}\right)}\right)}^2\times {\left(\frac{D_t^c\left({l}_{\tau },{k}_t,{e}_t,{y}_t\right)}{D_t^c\left({l}_{\tau },{k}_t,{e}_{\tau },{y}_t\right)}\right)}^2\hfill \\ {}\times {\left(\frac{D_t^c\left({l}_t,{k}_{\tau },{e}_t,{y}_t\right)}{D_t^c\left({l}_t,{k}_{\tau },{e}_{\tau },{y}_t\right)}\right)}^2\times {\left(\frac{D_t^c\left({l}_t,{k}_t,{e}_t,{y}_{\tau}\right)}{D_t^c\left({l}_t,{k}_t,{e}_{\tau },{y}_{\tau}\right)}\right)}^2\hfill \end{array}\right]}^{1/24}\hfill \\ {}\times {\left[\begin{array}{l}{\left(\frac{D_t^c\left({l}_t,{k}_t,{e}_t,{y}_t\right)}{D_t^c\left({l}_t,{k}_t,{e}_t,{y}_{\tau}\right)}\right)}^6\times {\left(\frac{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_{\tau },{y}_t\right)}{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_{\tau },{y}_{\tau}\right)}\right)}^6\hfill \\ {}\times {\left(\frac{D_t^c\left({l}_t,{k}_{\tau },{e}_{\tau },{y}_t\right)}{D_t^c\left({l}_t,{k}_{\tau },{e}_{\tau },{y}_{\tau}\right)}\right)}^2\times {\left(\frac{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_t,{y}_t\right)}{D_t^c\left({l}_{\tau },{k}_{\tau },{e}_t,{y}_{\tau}\right)}\right)}^2\hfill \\ {}\times {\left(\frac{D_t^c\left({l}_{\tau },{k}_t,{e}_{\tau },{y}_t\right)}{D_t^c\left({l}_{\tau },{k}_t,{e}_{\tau },{y}_{\tau}\right)}\right)}^2\times {\left(\frac{D_t^c\left({l}_t,{k}_{\tau },{e}_t,{y}_t\right)}{D_t^c\left({l}_t,{k}_{\tau },{e}_t,{y}_{\tau}\right)}\right)}^2\hfill \\ {}\times {\left(\frac{D_t^c\left({l}_t,{k}_t,{e}_{\tau },{y}_t\right)}{D_t^c\left({l}_{\tau },{k}_t,{e}_{\tau },{y}_{\tau}\right)}\right)}^2\times {\left(\frac{D_t^c\left({l}_{\tau },{k}_t,{e}_t,{y}_t\right)}{D_t^c\left({l}_{\tau },{k}_t,{e}_t,{y}_{\tau}\right)}\right)}^2\hfill \end{array}\right]}^{1/24}\hfill \\ {}=:L{E}_t^c\times K{E}_t^c\times E{S}_t^c\times O{S}_t^c\hfill \end{array} $$
(A.1)

Appendix 2

The whole decomposition of Eq. (9):

$$ \begin{array}{l}\frac{S_t\left({L}_t,{K}_t,{E}_t,{y}_t\right)}{S_t\left({L}_{\tau },{K}_{\tau },{E}_{\tau },{y}_{\tau}\right)}\hfill \\ {}={\left[\begin{array}{c}\hfill {\left(\frac{S_t\left({L}_t,{K}_t,{E}_t,{y}_t\right)}{S_t\left({L}_{\tau },{K}_t,{E}_t,{y}_t\right)}\right)}^6\times {\left(\frac{S_t\left({L}_t,{K}_{\tau },{E}_{\tau },{y}_{\tau}\right)}{S_t\left({L}_{\tau },{K}_{\tau },{E}_{\tau },{y}_{\tau}\right)}\right)}^6\hfill \\ {}\hfill \times {\left(\frac{S_t\left({L}_t,{K}_{\tau },{E}_{\tau },{y}_t\right)}{S_t\left({L}_{\tau },{K}_{\tau },{E}_{\tau },{y}_t\right)}\right)}^2\times {\left(\frac{S_t\left({L}_t,{K}_{\tau },{E}_t,{y}_{\tau}\right)}{S_t\left({L}_{\tau },{K}_{\tau },{E}_t,{y}_{\tau}\right)}\right)}^2\hfill \\ {}\hfill \times {\left(\frac{S_t\left({L}_t,{K}_t,{E}_{\tau },{y}_{\tau}\right)}{S_t\left({L}_{\tau },{K}_t,{E}_{\tau },{y}_{\tau}\right)}\right)}^2\times {\left(\frac{S_t\left({L}_t,{K}_{\tau },{E}_t,{y}_t\right)}{S_t\left({L}_{\tau },{K}_{\tau },{E}_t,{y}_t\right)}\right)}^2\hfill \\ {}\hfill \times {\left(\frac{S_t\left({L}_t,{K}_t,{E}_{\tau },{y}_t\right)}{S_t\left({L}_{\tau },{K}_t,{E}_{\tau },{y}_t\right)}\right)}^2\times {\left(\frac{S_t\left({L}_t,{K}_t,{E}_t,{y}_{\tau}\right)}{S_t\left({L}_{\tau },{K}_t,{E}_t,{y}_{\tau}\right)}\right)}^2\hfill \end{array}\right]}^{1/24}\hfill \\ {}\times {\left[\begin{array}{l}{\left(\frac{S_t\left({L}_t,{K}_t,{E}_t,{y}_t\right)}{S_t\left({L}_t,{K}_{\tau },{E}_t,{y}_t\right)}\right)}^6\times {\left(\frac{S_t\left({L}_{\tau },{K}_t,{E}_{\tau },{y}_{\tau}\right)}{S_t\left({L}_{\tau },{K}_{\tau },{E}_{\tau },{y}_{\tau}\right)}\right)}^6\hfill \\ {}\times {\left(\frac{S_t\left({L}_{\tau },{L}_t,{E}_{\tau },{y}_t\right)}{S_t\left({L}_{\tau },{K}_{\tau },{E}_{\tau },{y}_t\right)}\right)}^2\times {\left(\frac{S_t\left({L}_{\tau },{K}_t,{E}_t,{y}_{\tau}\right)}{S_t\left({L}_{\tau },{K}_{\tau },{E}_t,{y}_{\tau}\right)}\right)}^2\hfill \\ {}\times {\left(\frac{S_t\left({L}_t,{K}_t,{E}_{\tau },{y}_{\tau}\right)}{S_t\left({L}_t,{K}_{\tau },{E}_{\tau },{y}_{\tau}\right)}\right)}^2\times {\left(\frac{S_t\left({L}_{\tau },{K}_t,{E}_t,{y}_t\right)}{S_t\left({L}_{\tau },{K}_{\tau },{E}_t,{y}_t\right)}\right)}^2\hfill \\ {}\times {\left(\frac{S_t\left({L}_t,{K}_t,{E}_{\tau },{y}_{\tau}\right)}{S_t\left({L}_t,{K}_{\tau },{E}_{\tau },{y}_t\right)}\right)}^2\times {\left(\frac{S_t\left({L}_t,{K}_t,{E}_t,{y}_{\tau}\right)}{S_t\left({L}_t,{K}_{\tau },{E}_t,{y}_{\tau}\right)}\right)}^2\hfill \end{array}\right]}^{1/24}\hfill \\ {}\times {\left[\begin{array}{l}{\left(\frac{S_t\left({L}_t,{K}_t,{E}_t,{y}_t\right)}{S_t\left({L}_t,{K}_t,{E}_{\tau },{y}_t\right)}\right)}^6\times {\left(\frac{S_t\left({L}_{\tau },{K}_{\tau },{E}_t,{y}_{\tau}\right)}{S_t\left({L}_{\tau },{K}_{\tau },{E}_{\tau },{y}_{\tau}\right)}\right)}^6\hfill \\ {}\times {\left(\frac{S_t\left({L}_{\tau },{K}_{\tau },{E}_t,{y}_t\right)}{S_t\left({L}_{\tau },{K}_{\tau },{E}_{\tau },{y}_t\right)}\right)}^2\times {\left(\frac{S_t\left({L}_t,{K}_{\tau },{E}_t,{y}_{\tau}\right)}{S_t\left({L}_t,{K}_{\tau },{E}_{\tau },{y}_{\tau}\right)}\right)}^2\hfill \\ {}\times {\left(\frac{S_t\left({L}_{\tau },{K}_t,{E}_t,{y}_{\tau}\right)}{S_t\left({L}_{\tau },{K}_t,{E}_{\tau },{y}_{\tau}\right)}\right)}^2\times {\left(\frac{S_t\left({L}_{\tau },{K}_t,{E}_t,{y}_t\right)}{S_t\left({L}_{\tau },{K}_t,{E}_{\tau },{y}_t\right)}\right)}^2\hfill \\ {}\times {\left(\frac{S_t\left({L}_t,{K}_{\tau },{E}_t,{y}_t\right)}{S_t\left({L}_t,{K}_{\tau },{E}_{\tau },{y}_t\right)}\right)}^2\times {\left(\frac{S_t\left({L}_t,{K}_t,{E}_t,{y}_{\tau}\right)}{S_t\left({L}_t,{K}_t,{E}_{\tau },{y}_{\tau}\right)}\right)}^2\hfill \end{array}\right]}^{1/24}\hfill \\ {}\times {\left[\begin{array}{l}{\left(\frac{S_t\left({L}_t,{K}_t,{E}_t,{y}_t\right)}{S_t\left({L}_t,{K}_t,{E}_t,{y}_{\tau}\right)}\right)}^6\times {\left(\frac{S_t\left({L}_{\tau },{K}_{\tau },{E}_{\tau },{y}_t\right)}{S_t\left({L}_{\tau },{K}_{\tau },{E}_{\tau },{y}_{\tau}\right)}\right)}^6\hfill \\ {}\times {\left(\frac{S_t\left({L}_t,{K}_{\tau },{E}_{\tau },{y}_t\right)}{S_t\left({L}_t,{K}_{\tau },{E}_{\tau },{y}_{\tau}\right)}\right)}^2\times {\left(\frac{S_t\left({L}_{\tau },{K}_{\tau },{E}_t,{y}_t\right)}{S_t\left({L}_{\tau },{K}_{\tau },{E}_t,{y}_{\tau}\right)}\right)}^2\hfill \\ {}\times {\left(\frac{S_t\left({L}_{\tau },{K}_t,{E}_{\tau },{y}_t\right)}{S_t\left({L}_{\tau },{K}_t,{E}_{\tau },{y}_{\tau}\right)}\right)}^2\times {\left(\frac{S_t\left({L}_t,{K}_{\tau },{E}_t,{y}_t\right)}{S_t\left({L}_t,{K}_{\tau },{E}_t,{y}_{\tau}\right)}\right)}^2\hfill \\ {}\times {\left(\frac{S_t\left({L}_t,{K}_t,{E}_{\tau },{y}_t\right)}{S_t\left({L}_{\tau },{K}_t,{E}_{\tau },{y}_{\tau}\right)}\right)}^2\times {\left(\frac{S_t\left({L}_{\tau },{K}_t,{E}_t,{y}_t\right)}{S_t\left({L}_{\tau },{K}_t,{E}_t,{y}_{\tau}\right)}\right)}^2\hfill \end{array}\right]}^{1/24}\hfill \\ {}=:SAF{L}_t\times SAF{K}_t\times SAF{E}_t\times SAF{O}_t\hfill \end{array} $$
(B.1)

Appendix 3

Table 3 Industrial sectors and classification
Full size table

Appendix 4

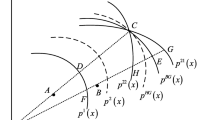
Note that for the Malmquist-type quantity index, geometric mean of distance changes relative to different production activities are calculated to avoid the ambiguity of choosing reference. The idea can be depicted in Fig. 4. The curves S t and S t + 1 represent the frontiers for time period t and t + 1, respectively. Points A and B represent the production activities at time period t and t + 1, respectively. Technological change between time period t and t + 1 can be measured as \( \frac{O{A}_1/O{A}_2}{O{A}_1/O{A}_3} \) when taking point A as reference. However, relative to point B, it is estimated as \( \frac{O{B}_1/O{B}_2}{O{B}_1/O{B}_3} \). To avoid different results initiated from different choosing references, geometric mean of \( \frac{O{A}_1/O{A}_2}{O{A}_1/O{A}_3} \) and \( \frac{O{B}_1/O{B}_2}{O{B}_1/O{B}_3} \) is calculated as the proxy of technological change. Furthermore, suppose that the production activity at time period t + 1 is point C instead of point B. It can be seen that point C is out of the production possibility set at time period t so that technological change cannot be measured based on point C. But, the calculation based on point A1 can partly reflect the movement of the frontier. This is the only useful information we can use. Thus, in this case, technological change can be measured as the distance change taking the production activity at time period t as reference. That is to say, technological change is estimated as \( \frac{O{A}_1/O{A}_2}{O{A}_1/O{A}_3} \), neglecting the information of point C.

Generally speaking, infeasibility occurs when production activity at time period t + 1 is out of the production possibility set at time t (like the case we described above). In our model, the indices of KE, LE, ES, OS, and TC are all Malmquist-type quantity index. Therefore, when some subcomponents are infeasible, we can exclude them from the calculation of geometric mean.

Fig. 4
figure 4

A graphical illustration of measuring technological change

Full size image

Another solution to the issue of infeasibility is conducting our decomposition based on the global DEA method proposed by Pastor and Lovell (2005). Analog to the derivation in section “Methodology”, one can easily get another version of our decomposition model with the global DEA method in which calculating cross-period distance functions is not needed so that it is free from the issue of infeasibility. However, the weakness of decomposing energy productivity change based on the global DEA method is that it cannot preclude technology regress.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Du, K., Huang, L. & Yang, Z. Understanding industrial energy productivity growth in China: a production-theoretical approach. Energy Efficiency 8, 493–508 (2015). https://doi.org/10.1007/s12053-014-9304-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12053-014-9304-4

Keywords

Search

Navigation