Skip to main content
SpringerLink
Log in

Application of temporal moments to interpret solute transport with time-dependent dispersion

  • Published:
Sādhanā Aims and scope Submit manuscript

Abstract

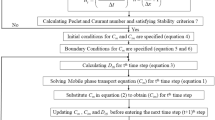
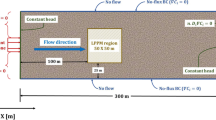
Temporal moments of solute transport through porous media are calculated to analyze the time average spatial distribution of solute plume. Simulation of spatially and temporally distributed breakthrough curves (BTCs) is computationally rigorous and lacking the explanation about overall plume evolution within porous media. However, temporal moment provides an attractive and simple solution to study the plume behavior. In this study, temporal moments are presented to interpret solute plume behavior in heterogeneous porous media such as hydraulically coupled stratified porous media with different time-dependent dispersion models. Governing equations of solute transport have been solved numerically using Crank-Nicolson scheme, and further solute concentration data has been utilized to calculate moments of solute concentration using numerical integration. The effect of various parameters such as mass-transfer coefficient, pore-water velocity, time-dependent dispersion coefficients, and porosity of mobile region on the transport of solute has been studied through sensitivity analyses. Temporal moment analysis revealed that the mass recovery, mean residence time, and variance are sensitive to the estimated parameters. Numerical results suggested that the asymptotic time-dependent dispersion function with mobile–immobile model represents the plume spreading through heterogeneous porous media in a more realistic manner.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7
Figure 8
Figure 9
Figure 10

Similar content being viewed by others

Abbreviations

\( C_{0} \) :

Injected concentration of solute source, (M/L3)

\( C_{m} \) :

Solute concentration in the mobile region at any time t, (M/L3)

\( C_{im} \) :

Solute concentration in the immobile region at any time t, (M/L3)

\( D_{\left( t \right)} \) :

Time-dependent hydrodynamic dispersion coefficient along the flow velocity, (L2/T)

\( D_{0} \) :

Maximum or uniform dispersion coefficient, (L2/T)

\( D_{m} \) :

Effective diffusion coefficient, (L2/T)

\( D_{macro} \left( x \right) \) :

Macro-dispersion coefficient calculated using second temporal moment

\( f \) :

Fraction of sorption sites that equilibrate instantly with the mobile regions

\( K_{A} \) :

Asymptotic time-dependent dispersion coefficient, (T)

\( K_{dm} \) :

Distribution coefficient of the linear sorption process in the mobile region, (L3/M)

\( K_{dim} \) :

Distribution coefficient of the linear sorption process in the immobile region, (L3/M)

\( K_{L} \) :

Linear time-dependent dispersion coefficient, (T)

\( M_{0} \) :

Zeroth absolute temporal moment

\( M_{1} \) :

First absolute temporal moment

\( M_{2} \) :

Second absolute temporal moment

\( M_{n} \) :

nth absolute temporal moment

\( \mu_{lm} \) :

First-order transformation coefficient for solution phase in the mobile region, (T−1)

\( \mu_{lim} \) :

First-order transformation coefficient for solution phase in the immobile region, (T−1)

\( \mu_{sm} \) :

First-order transformation coefficient for sorbed phase in the mobile region, (T−1)

\( \mu_{sim} \) :

First-order transformation coefficient for sorbed phase in the immobile region, (T−1)

\( \mu_{1} \) :

First normalized temporal moment

\( \mu_{2} \) :

Second normalized temporal moment

\( \mu_{n} \) :

nth order normalized temporal moment

\( \omega \) :

First order mass transfer coefficient (T−1)

\( q \) :

Flow rate, (L/T)

\( \rho_{b} \) :

Bulk density of the porous medium, (M/L3)

\( t \) :

Total simulation time, (T)

\( t_{p} \) :

Pulse duration, (T)

\( T_{1} \left( x \right) \) :

First temporal moment

\( T_{2} \left( x \right) \) :

Second central temporal moment

\( \theta_{m} \) :

Volumetric water content of the mobile region

\( \theta_{im} \) :

Volumetric water content of the immobile region

\( \theta \) :

Total volumetric water content of the porous media

\( v_{m} \) :

Mobile pore water velocity, (L/T)

\( V\left( x \right) \) :

Solute velocity calculated using first temporal moment

\( x \) :

Spatial coordinate taken in the direction of the fluid flow, (L)

ADE:

Advection dispersion equation

ADEA:

Advection-dispersion model with asymptotic time-dependent dispersion

ADEL:

Advection-dispersion model with linear time-dependent dispersion

MIM:

Mobile–immobile model

MIMA:

Mobile–immobile model with asymptotic time-dependent dispersion function

MIMC:

Mobile–immobile model with constant dispersion function

MIML:

Mobile–immobile model with linear time-dependent dispersion function

References

  1. Kitanidis P K 1994 The concept of the Dilution Index. Water Resour. Res. 30:2011–2026. https://doi.org/10.1029/94WR00762

    Article  Google Scholar 

  2. Kapoor V and Gelhar L W 1994 Transport in three-dimensionally heterogeneous aquifers: 1. Dynamics of concentration fluctuations. Water Resour. Res. 30:1775–1788. https://doi.org/10.1029/94WR00076

    Article  Google Scholar 

  3. Li Z and Brusseau M L 2000 Nonideal transport of reactive solutes in heterogeneous porous media - 6. Microscopic and macroscopic approaches for incorporating heterogeneous rate-limited mass transfer. Water Resour. Res. 36:2853–2867. https://doi.org/10.1029/2000WR900089

    Article  Google Scholar 

  4. Srivastava R and Brusseau M L 1996 Nonideal transport of reactive solutes in heterogeneous porous media: 1. Numerical model development and moments analysis. J. Contam. Hydrol. 24:117–143. https://doi.org/10.1016/S0169-7722(96)00039-3

    Article  Google Scholar 

  5. Logan J D 1996 Solute transport in porous media with scale-dependent dispersion and periodic boundary conditions. J. Hydrol. 184:261–276. https://doi.org/10.1016/0022-1694(95)02976-1

    Article  Google Scholar 

  6. Ballarini E, Bauer S, Eberhardt C and Beyer C 2014 Evaluation of the Role of Heterogeneities on Transverse Mixing in Bench-Scale Tank Experiments by Numerical Modeling. Groundwater 52:368–377. https://doi.org/10.1111/gwat.12066

    Article  Google Scholar 

  7. Bons P D, van Milligen B P and Blum P 2013 A general unified expression for solute and heat dispersion in homogeneous porous media. Water Resour. Res. 49:6166–6178. https://doi.org/10.1002/wrcr.20488

    Article  Google Scholar 

  8. Chen J S, Liu C W and Liang C P 2006 Evaluation of longitudinal and transverse dispersivities/distance ratios for tracer test in a radially convergent flow field with scale-dependent dispersion. Adv. Water Resour. 29:887–898. https://doi.org/10.1016/j.advwatres.2005.08.001

    Article  Google Scholar 

  9. Sharma P K, Sekhar M, Srivastava R and Ojha C S P 2012 Temporal Moments for Reactive Transport through Fractured Impermeable / Permeable Formations. J. Hydrol. Eng. 17:1302–1314. https://doi.org/10.1061/(ASCE)HE.1943-5584.0000586

    Article  Google Scholar 

  10. Pang L, Goltz M and Close M 2003 Application of the method of temporal moments to interpret solute transport with sorption and degradation. J. Contam. Hydrol. 60:123–134. https://doi.org/10.1016/S0169-7722(02)00061-X

    Article  Google Scholar 

  11. Valocchi A J 1990 Use of temporal moment analysis to study reactive solute transport in aggregated porous media. Geoderma 46:233–247

    Article  Google Scholar 

  12. Yu C, Warrick A W and Conklin M H 1999 A moment method for analyzing breakthrough curves of step inputs. Water Resour. Res. 35:3567–3572. https://doi.org/10.1029/1999WR900225

    Article  Google Scholar 

  13. Pang L, Close M and Noonan M 1998 Rhodamine WT and Bacillus subtilis Transport through an Alluvial Gravel Aquifer. Ground Water 36:112–122. https://doi.org/10.1111/j.1745-6584.1998.tb01071.x

    Article  Google Scholar 

  14. Renu V and Suresh Kumar G 2016 Temporal Moment Analysis of Multi-Species Radionuclide Transport in a Coupled Fracture-Skin-Matrix System with a Variable Fracture Aperture. Environ. Model Assess. 21:547–562. https://doi.org/10.1007/s10666-016-9515-5

    Article  Google Scholar 

  15. Cunningham J A and Roberts P V 1998 Use of temporal moments to investigate the effects of nonuniform grain-size distribution on the transport of sorbing solutes. Water Resour. Res. 34:1415–1425

    Article  Google Scholar 

  16. Suresh Kumar G 2014 Mathematical Modeling of Groundwater Flow and Solute Transport in Saturated Fractured Rock Using a Dual-Porosity Approach. J. Hydrol. Eng. 19:04014033. https://doi.org/10.1061/(ASCE)HE.1943-5584.0000986

    Article  Google Scholar 

  17. Govindaraju R S, Das B S 2007 Moment Analysis For Subsurface Hydrologic Applications. Springer Netherlands, Dordrecht

    MATH  Google Scholar 

  18. Naff R L 1992 Arrival times and temporal moments of breakthrough curves for an imperfectly stratified aquifer. Water Resour. Res. 28:53–68. https://doi.org/10.1029/91WR02105

    Article  Google Scholar 

  19. Valocchi A J 1985 Validity of the Local Equilibrium Assumption for Modeling Sorbing Solute Transport Through Homogeneous Soils. Water Resour. Res. 21:808–820. https://doi.org/10.1029/WR021i006p00808

    Article  Google Scholar 

  20. Joshi N, Ojha C S P, Sharma P K and Madramootoo C A 2015 Application of nonequilibrium fracture matrix model in simulating reactive contaminant transport through fractured porous media. Water Resour. Res. 51:390–408. https://doi.org/10.1002/2014WR016500/abstract

  21. Renu V and Kumar G S 2014 Temporal moment analysis of solute transport in a coupled fracture-skin-matrix system. Sadhana 39:487–509. https://doi.org/10.1007/s12046-014-0240-y

  22. Sharma P K, Ojha C S P and Joshi N 2014 Finite volume model for reactive transport in fractured porous media with distance- and time-dependent dispersion. Hydrol. Sci. J. 59:1582–1592. https://doi.org/10.1080/02626667.2014.932910

    Article  Google Scholar 

  23. Kumar G S, Sekhar M and Misra D 2006 Time dependent dispersivity behavior of non-reactive solutes in a system of parallel fractures. Hydrol. Earth Syst. Sci. Discuss. 3:895–923. https://doi.org/10.5194/hessd-3-895-2006

    Article  Google Scholar 

  24. Jaiswal D K, Kumar A, Kumar N and Yadav R R 2009 Analytical solutions for temporally and spatially dependent solute dispersion of pulse type input concentration in one-dimensional semi-infinite media. J. Hydro-Environment Res. 2:254–263. https://doi.org/10.1016/j.jher.2009.01.003

  25. Barry D A and Sposito G 1989 Analytical Solution of a Convection-Dispersion Model With Time-Dependent Transport Coefficients. Water Resour Res. 25:2407–2416

    Article  Google Scholar 

  26. Natarajan N 2016 Effect of distance-dependent and time-dependent dispersion on non-linearly sorbed multispecies contaminants in porous media. ISH J. Hydraul. Eng. 22:16–29. https://doi.org/10.1080/09715010.2015.1043597

    Article  Google Scholar 

  27. Basha H A and El‐Habel F S 1993 Analytical solution of the one‐dimensional time‐dependent transport equation. Water Resour. Res. 29:3209–3214. https://doi.org/10.1029/93WR01038

    Article  Google Scholar 

  28. van Genuchten M T and Wierenga P J 1976 Mass Transfer Studies in Sorbing Porous Media I. Analytical Solutions. Soil Sci. Soc. Am. J. 40:473–480. https://doi.org/10.2136/sssaj1976.03615995004000040011x

    Article  Google Scholar 

  29. van Genuchten M T and Wierenga P J 1977 Mass Transfer Studies in Sorbing Porous Media: II. Experimental Evaluation with Tritium. Soil Sci. Soc. Am. J. 41:272–278

    Article  Google Scholar 

  30. Guleria A, Swami D, Sharma A and Sharma S 2019 Non-reactive solute transport modelling with time-dependent dispersion through stratified porous media. Sādhanā 44:81. https://doi.org/10.1007/s12046-019-1056-6

    Article  MathSciNet  Google Scholar 

  31. Zheng C and Bennett G D 2002 Applied Contaminant Transport Modeling, 2nd ed. Wiley-Interscience, New York

    Google Scholar 

  32. Swami D, Sharma P K and Ojha C S P 2016 Behavioral Study of the Mass Transfer Coefficient of Nonreactive Solute with Velocity, Distance, and Dispersion. J. Environ. Eng. 143:1–10. https://doi.org/10.1061/(ASCE)EE.1943-7870.0001164

    Article  Google Scholar 

Download references

Acknowledgements

All the work has been carried out at Indian Institute of Technology, Mandi during Master’s study of first author. First author would like to thank Indian Institute of Technology, Mandi for supporting this study. The authors would like to thank the reviewer and editor for their constructive and valuable comments.

Author information

Authors and Affiliations

  1. School of Engineering, Indian Institute of Technology Mandi, Kamand, 175005, India

    Abhay Guleria, Deepak Swami & Abhimanyu Sharma

  2. Department of Civil Engineering, Indian Institute of Technology Jammu, Jammu, 181221, India

    Nitin Joshi

Authors
  1. Abhay Guleria
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Deepak Swami
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nitin Joshi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Abhimanyu Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Abhay Guleria.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Guleria, A., Swami, D., Joshi, N. et al. Application of temporal moments to interpret solute transport with time-dependent dispersion. Sādhanā 45, 159 (2020). https://doi.org/10.1007/s12046-020-01402-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12046-020-01402-5

Keywords

Search

Navigation