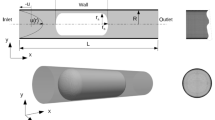
Abstract
Experimental investigations are reported for pulsating Taylor bubble (PTB) flow through a 2.12 mm horizontal circular minichannel. Air and water are used as working fluids. A T-junction is used to generate Taylor bubble flow in a minichannel. The superficial gas velocity (U SG ) is kept as 0.0472 m/s. The superficial liquid velocity (U SL ) is kept as 0.0472 and 0.0708 m/s. The pulsating liquid flow is generated by developing a pulse generator circuit. The investigations are carried out for various pulsating flow frequencies of 0 Hz (continuous flow), 0.1, 0.25, 0.5, 1 and 2 Hz, which correspond to Womersley number (W o ) 0, 0.84, 1.39, 1.88, 2.65 and 3.75, respectively. Heat transfer enhancement is found to be negligible (less than 1%) for pulsating laminar liquid flow through the minichannel. On the contrary, heat transfer is observed to decrease by 35% for PTB flow compared with continuous Taylor bubble (CTB) flow for imposed frequency of pulsation up to 1 Hz.

















Similar content being viewed by others
Abbreviations
- c :
-
specific heat, J kg−1 K−1
- d h :
-
diameter of circular pipe, m
- f :
-
frequency, Hz
- h :
-
heat transfer coefficient, W m−1 K−1
- k :
-
thermal conductivity, W m−2 K−1
- L :
-
length of heating section, m
- L * :
-
non-dimensional axial length
- m · :
-
mass flow rate, kg s−1
- Q :
-
heat input, W
- q ′ :
-
heat flux, W m−2
- t :
-
time, s
- T :
-
imposed time period of fluctuation, s
- T * :
-
non-dimensional time period
- T * f :
-
non-dimensional fluid temperature
- T * w :
-
non-dimensional wall temperature
- U :
-
velocity, m s−1
- t c :
-
thermal diffusivity time scale, s
- x :
-
distance from heating section
- ω :
-
angular velocity, rad s−1
- α :
-
thermal diffusivity, m2 s−1
- μ :
-
dynamic viscosity, Pa s
- ρ :
-
mass density, kg m−3
- β :
-
homogeneous void fraction
- Re :
-
Reynolds number
- Nu :
-
Nusselt number
- W o :
-
Womersley number \( \left( {0.5d_{h} \sqrt {\frac{\omega }{\upsilon }} } \right) \)
- x * :
-
inverse Graetz number
- g :
-
gas (air)
- l :
-
liquid
- tp :
-
two phase
- sl :
-
superficial liquid
- sg :
-
superficial gas
- *:
-
dimensionless
References
Akachi H 1990 Patent No. 4,921,041, May 1, United States of America
Akachi H 1993 Patent No. 5,219,020, June 15, United States of America
Zhang Y and Faghri A 2002 Heat transfer in pulsating heat pipe with open end. Int. J. Heat Mass Transf. 45: 755–764
Khandekar S, Gautam A P and Sharma P K 2009 Multiple quasi-steady states in a closed loop pulsating heat pipe. Int. J. Therm. Sci. 48: 535–546
Khandekar S and Groll M 2004 An insight into thermo-hydraulic coupling in pulsating heat pipe. Int. J. Therm. Sci. 43(1): 13–20
Patel V M, Gaurav and Mehta H B 2017 Influence of working fluids on startup mechanism and thermal performance of a closed loop pulsating heat pipe. Appl. Therm. Eng. 110: 1568–1577
Zhang Y and Faghri A 2008 Advances and unresolved issues in pulsating heat pipe. Heat Transf. Eng. 29(1): 20–44
Mehta B and Khandekar S 2014 Taylor bubble flows and heat transfer in the context of pulsating heat pipes. Int. J. Heat Mass Transf. 79: 279–290
Mehta H B and Banerjee J 2016 Experimental investigations on thermo-hydrodynamics of continuous Taylor bubble flow through minichannel. Int. J. Heat Mass Transf. 94: 119–137
Kline S J and McClintock K N 1953 The descriptions of uncertainties in single sample experiments. Mech. Eng. 75: 3–8
Muzychka Y S and Yovanovich M M 2004. Force convection heat transfer in the combined entry region of non-circular ducts. ASME J. Heat Transf. 126: 54–61
Womersley J R 1955 Method for the calculation of velocity rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. 127: 553–563
Yu J and Zhao T S 2004 An analytical study of pulsating laminar heat convection in circular tube with constant heat flux. Int. J. Heat Mass Transf. 47: 5297–5301
Acknowledgements
The authors would like to thank the authorities of the Sardar Vallabhbhai National Institute of Technology, Surat, for providing financial support for the development of Advanced Fluid Dynamics Lab, where this minichannel-based experiments were conducted.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sagar, K., Mehta, H.B. Experimental investigations on heat transfer characteristics of pulsating single-phase liquid flow and two-phase Taylor bubble flow through a minichannel. Sādhanā 43, 47 (2018). https://doi.org/10.1007/s12046-018-0827-9
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12046-018-0827-9