Skip to main content
SpringerLink
Log in

Multiple solutions for non-Newtonian nanofluid flow over a stretching sheet with nonlinear thermal radiation: Application in transdermal drug delivery

  • Published:
Pramana Aims and scope Submit manuscript

Abstract

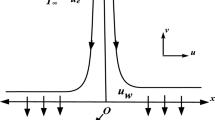
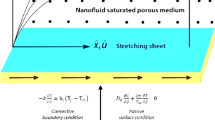
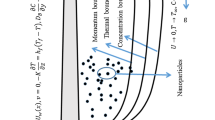
We have explored multiple solutions for non-Newtonian Casson nanofluid flow past a moving extending sheet under the influence of variable thermal conductivity and nonlinear radiation through a permeable medium with convective boundary conditions. The governing equations are transformed to ODEs by similarity transformations and then solved numerically by the Chebyshev pseudospectral (CPS) method. Dual solutions are obtained for velocity, temperature and nanoparticle concentration distributions with different values of physical parameters. In the present analysis, it was found that, the nonlinearity formula for thermal radiation gives a realistic description of nanofluid mathematical model depending on the existence of nanoscale particles. Furthermore, the concentration of nanoparticles is highly influenced by nonlinear thermal radiation due to the sizes of nanofluid, where linear radiation has a weak effect on the concentration distributions of nanoparticles. These results are very important in medicine, and more specifically for reinforcing the delivery of drugs through the skin, as the nanoparticle entrapment of drugs enhances delivery to, or absorption by, target cells. The transdermal drug delivery system offers huge clinical advantages over other dosage forms. As transdermal drug delivery offers controlled as well as predetermined rate of release of the drug into the patient, it can keep up steady-state nanofluid concentration.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23

Similar content being viewed by others

References

  1. V Nagendramma and A L Ratnam, Int. J. Pure Appl. Math. 113, 29 (2017)

    Google Scholar 

  2. N Bachok, N Najib, N Md Arifin and N Senu, WSEAS Trans. Fluid Mech. 11, 151 (2016)

    Google Scholar 

  3. K Sreelakshmi and G Sarojamma, Transactions of A. Razmadze Mathematical Institute 172, 606 (2018)

    MathSciNet  Google Scholar 

  4. A Tanveera, T Salahuddina, M Khanc, A S Alshomranid and M Y Malikb, Results Phys. 9, 916 (2018)

    ADS  Google Scholar 

  5. F M Abbasi, I Shanakhat and S A Shehzad, J. Magn. Magn. Mater. 474, 434 (2019)

    ADS  Google Scholar 

  6. A Sarlak, A Ahmadpour and M R Hajmohammadi, Appl. Therm. Eng. 147, 205 (2019)

    Google Scholar 

  7. H Ajam, S S Jafari and N Freidoonimehr, Ain Shams Eng. J. 9, 525 (2018)

    Google Scholar 

  8. P Rana, N Shukla, Y Gupta and I Pop, Phys. Lett. A 383, 176 (2019)

    ADS  MathSciNet  Google Scholar 

  9. A A Afify and M Abd El-Aziz, Pramana – J. Phys. 88: 31(2017)

  10. E H Aly, Powder Technol. 342, 528 (2019)

    Google Scholar 

  11. M N Rostami, S Dinarv and I Pop, Chin. J. Phys. 56, 2465 (2018)

    Google Scholar 

  12. H Mondal, M Almakki and P Sibanda, J. Comput. Design Eng. https://doi.org/10.1016/j.jcde.2019.01.003 (2019)

  13. M Khan, M Irfan, L Ahmad and W A Khan, Phys. Lett. A 382, 2334 (2018)

    ADS  MathSciNet  Google Scholar 

  14. P Rana, N Shukla, Y Gupta and I Pop, Commun. Nonlinear Sci. Numer. Simul. 66, 183 (2019)

    ADS  MathSciNet  Google Scholar 

  15. P Rana, R Dhanai and L Kumar, Adv. Powder Technol. 28, 1727 (2017)

    Google Scholar 

  16. R Dhanai, P Rana and L Kumar, J. Taiwan Inst. Chem. Eng. 66, 283 (2016)

    Google Scholar 

  17. R Dhanai, P Rana and L Kumar, Eur. Phys. J. Plus 131, 142 (2016)

    Google Scholar 

  18. R Dhanai, P Rana and L Kumar, Powder Technol. 288, 140 (2016)

    Google Scholar 

  19. R Dhanai, P Rana and L Kumar, J. Taiwan Inst. Chem. Eng. 58, 155 (2016)

    Google Scholar 

  20. D Pala and G Mandal, J. Propul. Power Res. 6, 58 (2017)

    Google Scholar 

  21. D Srinivasacharyan and P V Kumar, J. Propul. Power Res. 7, 147 (2018)

    Google Scholar 

  22. M Alizadeha, A S Dogonchib and D D Ganjia, Case Stud. Therm. Eng. 12, 319 (2018)

    Google Scholar 

  23. G C Sankad and I Maharudrappa, Lecture notes in mechanical engineering (Springer Nature, Singapore, 2019), https://doi.org/10.1007/978-981-13-1903-7_20

  24. M Khan, A Shahid, T Salahuddin, M Y Malik and M Mushtaq, J. Braz. Soc. Mech. Sci. Eng. 40, 533 (2018)

    Google Scholar 

  25. S Jain and R Choudhary, Lecture notes in mechanical engineering (Springer Nature, Singapore, 2019), https://doi.org/10.1007/978-981-13-1903-7_40

  26. M S Aghighi, A Ammar, C Metivier and M Gharagozlu, Int. J. Therm. Sci. 127, 79 (2018)

    Google Scholar 

  27. F Mabood and K Das, Heliyon5(2), 201216 (2019)

    Google Scholar 

  28. J Raza, Propul. Power Res. 8, 138 (2019)

    Google Scholar 

  29. T Thumma, S R Mishra and M D Shamshuddin, Lecture notes in mechanical engineering (Springer Nature, Singapore, 2019), https://doi.org/10.1007/978-981-13-1903-7_66

  30. H J Xu, Z B Xing, F Q Wang and Z M Cheng, Chem. Eng. Sci. 195, 462 (2019)

    Google Scholar 

  31. B K Jha, B Y Isah and I J Uwanta, Ain Shams Eng. J. 9, 1069 (2018)

    Google Scholar 

  32. R Sachan and M Bajpai, Int. J. Res. Development Pharmacy Life Sci. 3, 748 (2013)

    Google Scholar 

  33. M Nakamura and T Sawada, J. Biomech. 110, 137 (1988)

    Google Scholar 

  34. N T M Eldabe, M F El-Sayed, A Y Ghaly and H M Sayed, Physica A 383, 253 (2007)

    ADS  Google Scholar 

  35. E F Elshehawey, N T Eldabe, E M E Elbarbary and N S Elgazery, Can. J. Phys. 82, 701 (2004)

    ADS  Google Scholar 

  36. H Sithole, H Mondal, S Goqo, P Sibanda and S Motsa, Appl. Math. Comput. 339, 820 (2018)

    MathSciNet  Google Scholar 

  37. J C Slattery, Momentum, energy and mass transfer in continua (McGraw-Hill, New York, 1972)

    Google Scholar 

  38. S R R C Babu, S Venkateswarlu and K J Lakshmi, Int. J. Appl. Eng. Res. 13, 13989 (2018)

    Google Scholar 

  39. N T Eldabe, E F Elshehawey, E M E Elbarbary and N S Elgazery, Appl. Math. Comput. 160, 437 (2005)

    MathSciNet  Google Scholar 

  40. K Bhattacharyya, M S Uddin and G C Layek, Alex. Eng. J. 55, 1703 (2016)

    Google Scholar 

  41. M A Snyder, Chebyshev methods in numerical approximation (Prentice-Hall, USA, 1966)

    MATH  Google Scholar 

  42. L Fox and I B Parker, Chebyshev polynomials in numerical analysis (Oxford University Press, London, 1968)

    MATH  Google Scholar 

  43. D Gottlieb and S A Orszag, Numerical analysis of spectral methods: Theory and applications, CBMS-NSF Regional Conference Series in Applied Mathematics 26 (Philadelphia, PA: SIAM, 1977)

    Google Scholar 

  44. R G Voigt, D Gottlieb and M Y Hussaini, Spectral methods for partial differential equations (SIAM, Philadelphia, PA, 1984)

    Google Scholar 

  45. C Canuto, M Y Hussaini, A Quarterini and T A Zang, Spectral methods in fluid dynamics (Springer-Verlag, Berlin, 1988)

    MATH  Google Scholar 

  46. J P Boyd, Chebyshev and Fourier spectral methods (Dover, New York, 2000)

    Google Scholar 

  47. N S Elgazery, J. Egypt. Math. Soc.27, 39 (2019)

    MathSciNet  Google Scholar 

  48. A Saadatmandi and M Dehghan, Phys. Lett. A372, 4037 (2008)

    ADS  Google Scholar 

  49. K H Huang, R Tsai and C H Huang, J. Non-Newtonian Fluid Mech.165, 1351 (2010)

    Google Scholar 

  50. E M E Elbarbary and S M El-Sayed, Appl. Numer. Math.55, 425 (2005)

    MathSciNet  Google Scholar 

  51. E H Doha, J. Comput. Math. Appl.21, 115 (1991)

    MathSciNet  Google Scholar 

  52. M Hamid, M Usmanb, Z H Khane, R Ahmad and W Wang, Phys. Lett. A383, 2400 (2019)

    ADS  MathSciNet  Google Scholar 

  53. A Zaib, K Bhattacharyya, M Uddin and S Shafie, Model. Simul. Eng.4, 1 (2016)

    Google Scholar 

  54. A Falana, O A Ojewale and T B Adeboje, Adv. Nanoparticles5, 123 (2016)

    Google Scholar 

Download references

Acknowledgements

The authors are thankful to the reviewers for their constructive suggestions and encouraging comments to improve the final form of this manuscript.

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Education, Ain Shams University, El Makrizy St., Roxy, Cairo, 11566, Egypt

    Nasser S Elgazery & Asmaa F Elelamy

Authors
  1. Nasser S Elgazery
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Asmaa F Elelamy
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nasser S Elgazery.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Elgazery, N.S., Elelamy, A.F. Multiple solutions for non-Newtonian nanofluid flow over a stretching sheet with nonlinear thermal radiation: Application in transdermal drug delivery. Pramana - J Phys 94, 68 (2020). https://doi.org/10.1007/s12043-020-1925-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12043-020-1925-x

Keywords

PACS Nos

Search

Navigation